The document presents Graph Neural Prompting (GNP), a novel plug-and-play method aimed at enhancing large language models (LLMs) by integrating beneficial knowledge from knowledge graphs (KGs). It addresses the challenges of combining KGs with LLMs, particularly concerning noise and model architecture complexities. Through experiments in commonsense and biomedical reasoning, the authors demonstrate the efficacy of GNP in improving LLM performance.

1. GNP
Graph Neural Prompting with Large Language
Models
AAAI, 2024
Yijun Tian, Huan Song, Zichen Wang et al.
Speaker: Po-Chuan Chen
Jun 4, 2024
1 / 38

2. GNP
Table of contents
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
5 Experiments
6 Conclusion
2 / 38

3. GNP
Abstract
Table of contents
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
5 Experiments
6 Conclusion
3 / 38

4. GNP
Abstract
Abstract
To reduce the limitation of the large language model, the existing
work enhances pre-trained LLMs using grounded knowledge.
For example, retrieval-augmented generation, remains an open
question, knowledge graphs (KG).
In this paper, they propose graph neural prompting (GNP), a
plug-and-play method to help pre-trained LLMs gain beneficial
knowledge from KGs.
4 / 38

5. GNP
Introduction
Table of contents
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
5 Experiments
6 Conclusion
5 / 38

6. GNP
Introduction
Introduction
Knowledge graphs (KGs) store enormous facts and serve as a
systematic way of presenting knowledge [2].
Existing methods [4] have incorporated KGs with language models by
designing customized model architectures to accommodate both
textual data and KGs.
The joint training model becomes challenging due to the parameter
size of the language model.
6 / 38

7. GNP
Introduction
Introduction (Cont.)
A direct way to combine the benefit of KGs and the language model
feeding the KG triples1 into LLMs [1].
However, this method can introduce substantial noise since KGs might
contain various extraneous contexts.
Can we learn beneficial knowledge from KGs
and integrate them into pre-trained LLMs?
1KG triples are structured data elements consisting of a subject, predicate, and
object, representing relationships between entities in a Knowledge Graph.
7 / 38

8. GNP
Introduction
Graph Neural Prompting
They propose a method that retrieves and encodes the pertinent
grounded knowledge to derive a Graph Neural Prompt.
The prompt is an embedding vector that can be sent to LLMs for
guidance and instructions.
8 / 38

9. GNP
Introduction
Figure 1: Reported results are averaged across six datasets on two tasks for
an 11B FLAN-T5 model.
9 / 38

10. GNP
Preliminary
Table of contents
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
5 Experiments
6 Conclusion
10 / 38

11. GNP
Preliminary
Knowledge Graph
A knowledge graph is defined as G = (E, R, T).
E is the set of entities.
R is the set of relations.
T is the collection of fact tripes {(eh, r, et)} ∈ E × R × E, where
eh is the head entity, r is the relation, and et is the tail entity.
11 / 38

12. GNP
Preliminary
Multiple Choice Question Answering
Given a question Q, a set of answer options A = {ak}K
k=1, and an
optional context C. The ground truth label y ∈ A is the correct answer.
We need to design a model FΘ that selects the best option to answer
the question. In addition, this paper uses knowledge graph G to
provide external knowledge and help the model to answer the question.
12 / 38

13. GNP
Methodology
Table of contents I
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
Prompting LLMs for Question Answering
Subgraph Retrieval
Graph Neural Prompting
5 Experiments
13 / 38

14. GNP
Methodology
Table of contents II
6 Conclusion
14 / 38

15. GNP
Methodology
Prompting LLMs for Question Answering
Prompting LLMs for Question Answering
Below are the steps:
1 Tokenizing the concatenation of C, Q, A into a sequence of input
text tokens X.
2 Designing a series of prompt tokens P, pretending it to the input
tokens X. Using it as input for the LLM model to generate
prediction y′ = f ([P, X]).
3 The model can be trained for downstream task adaptation using
standard maximum likelihood loss using teacher forcing and a
cross-entropy loss Lllm = − log p(y | X, Θ).
15 / 38

16. GNP
Methodology
Prompting LLMs for Question Answering
Prompting LLMs for Question Answering (Cont.)
This paper provides a prompt method not using text, but structural and
factual information contained in the knowledge graph G into a soft
prompt.
They concatenate the soft prompt with the token embeddings of X.
16 / 38

17. GNP
Methodology
Subgraph Retrieval
Subgraph Retrieval
They retrieve subgraphs of G that contain the relevant entities to the
token in X.
Based on corresponding context C and question Q, each answer
option ak. They find a set of matched entities Ematch via entity linking
to match tokens in X to the entity in G.
After that, they retrieve a subgraph G′ by using Ematch with their
two-hop neighbors and the relations that connect them.
17 / 38

18. GNP
Methodology
Graph Neural Prompting
Figure 2: The overall framework.
18 / 38

19. GNP
Methodology
Graph Neural Prompting
GNP’s Module
1 Graph Neural Network Encoder
2 Cross-modality pooling
3 Domain Projector
4 Self-supervised Link Prediction
19 / 38

20. GNP
Methodology
Graph Neural Prompting
GNN Encoder
They introduce a GNN to encode the most relevant knowledge and
integrate the relationships among the entities.
Firstly, they initialize the node embeddings using pre-trained entity
embeddings.
Then, they employ a standard graph attention network as their GNN
encoder for the subgraph G′.
H1 = fGNN (G′
)
where H1 ∈ Rdg represents the learned node embeddings, and dg is the
output dimension of the GNN encoder.
20 / 38

21. GNP
Methodology
Graph Neural Prompting
Cross-modality Pooling
They design the cross-modality pooling to identify the most pertinent
nodes related to the question. They use a self-attention layer first.
H2 = Self-Attn(H1)
Second, they leverage the text prompt, which obtains as text
embeddings T ∈ Rdt to calculate the importance of nodes within the
graph, where dt is the dimension of the LLM dictionary.
Additionally, they apply a transformation for T to match the
dimension dg.
21 / 38

22. GNP
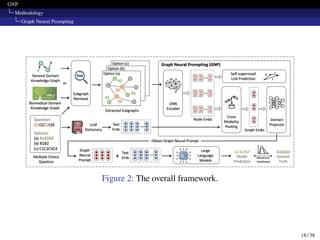
Methodology
Graph Neural Prompting
Cross-modality Pooling (Cont.)
Then, they calculate the cross-modality attention using H2 and T′.
H3 = softmax[H2 · (T′
)T
/
√︁
dg] · T ′
where T′ = FFN1(𝜎(FFN2(T))), 𝜎 is the GELU activation function.
Finally, they generate graph-level embedding by average pooling the
node embeddings H3 in G′.
H4 = POOL(H3)
22 / 38

23. GNP
Methodology
Graph Neural Prompting
Domain Projector
To create a mapping between the graph-level embeddings and the text
domain to facilitate comprehension by the LLM, they design a domain
projector to align them.
In addition, the projector needs to consider the dimension size of
LLM, such that the projector is designed as follows:
Z = FFN3(𝜎(FFN4(H4)))
where Z is the Graph Neural Prompt.
23 / 38

24. GNP
Methodology
Graph Neural Prompting
Self-supervised Link Prediction
In this section, they design an objective function to enable the model
to learn and adapt to the target dataset.
They mask some edges from G′ and enforce the model to predict
them, which the set of masked-out edges as Emask ⊆ E.
They adopt a widely used knowledge graph embedding method
DistMult [3] to map the entity embeddings and relation in the KG to
vectors, h, r, t, where entity from H3.
24 / 38

25. GNP
Methodology
Graph Neural Prompting
Self-supervised Link Prediction (Cont.)
To distinguish between correct positive triples and incorrect negative
triples, a scoring function 𝜙(eh, et) = ⟨h, r, t⟩ is defined, where ⟨·, ·, ·⟩
denotes the trilinear dot product and r represents the relations in
knowledge graphs (KGs).
The model is trained to predict the masked edges in Emask as positive
samples, while other randomly selected edges are treated as negative
samples.
Llp =
∑︁
(eh,r,et )∈Emask
(Spos + Sneg)
25 / 38

26. GNP
Methodology
Graph Neural Prompting
Self-supervised Link Prediction (Cont.)
Llp =
∑︁
(eh,r,et )∈Emask
(Spos + Sneg)
where Spos = − log 𝜎s(𝜙(eh, et) + 𝛾), and 𝛾 is margin, 𝜎s is the
sigmoid function. Sneg = 1
n
Í
(e′
h
,r,e′
t ) log 𝜎s(𝜙(e′
h, e′
t) + 𝛾), {(e′
h, r, e′
t)}
are n negative triples.
The final objective function:
L = Lllm + 𝜆Llp
where 𝜆 is a trade-off weight for balancing two losses.
26 / 38

27. GNP
Experiments
Table of contents
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
5 Experiments
6 Conclusion
27 / 38

28. GNP
Experiments
Experiment setup
Knowledge Graphs and Datasets
1 General domain (commonsense reasoning)
2 Biomedical domain (biomedical reasoning)
Two Settings
1 LLM Frozen
2 LLM Tuned
Baselines
1 LLM-only
2 Hard prompts (three prompt design methods)
3 KG Flattening
4 One-hop (OH) and two-hop (TH)
5 Prompt tuning (soft prompts)
28 / 38

29. GNP
Experiments
Table 1: Overall experimental results on commonsense reasoning and
biomedical reasoning tasks.
29 / 38

30. GNP
Experiments
Ablation Study
Analyzing the contributions of different components by removing
each of them independently.
Table 2: Results of ablation study.
30 / 38

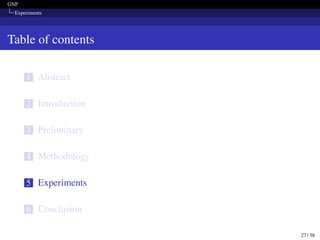
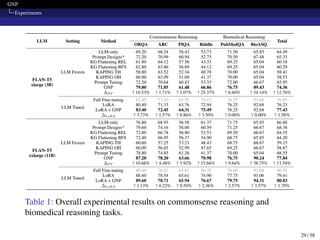
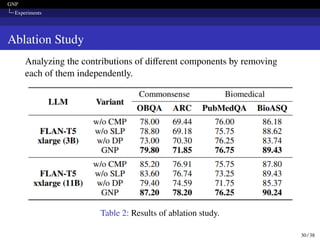
31. GNP
Experiments
Model Design Comparison
For prompt tuning, they use dataset-level prompt (DLP). For modeling
relations, they use Relational GNN (RGNN) [5].
Table 3: Results of integrating different model designs.
31 / 38

32. GNP
Experiments
Impact of GNN layers
They evaluate the influence of GNN layers for both 3B and 11B
models.
Figure 3: Performance w.r.t. different number of GNN layers.
32 / 38

33. GNP
Experiments
Impact of cross-modality pooling layers
They report the performance of different cross-modality pooling
layers.
Figure 4: Performance w.r.t. different number of cross-modality pooling
layers.
33 / 38

34. GNP
Experiments
Case Study and Visualization
They select two examples from the OBQA dataset and visualize the
retrieved subgraphs.
Figure 5: Case study on two QA examples from OBQA dataset.
34 / 38

35. GNP
Conclusion
Table of contents
1 Abstract
2 Introduction
3 Preliminary
4 Methodology
5 Experiments
6 Conclusion
35 / 38

36. GNP
Conclusion
Conclusion
They propose Graph Neural Prompting (GNP), a novel plug-and-play
method to assist pre-trained LLMs in learning beneficial knowledge
from KGs.
36 / 38

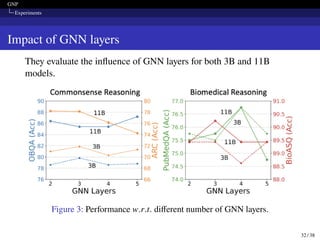
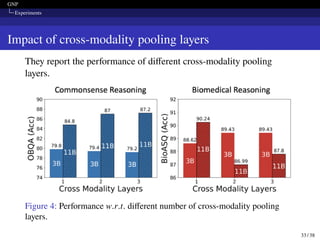
37. GNP
Conclusion
References I
[1] Jinheon Baek, Alham Fikri Aji, et al. “Knowledge-Augmented
Language Model Prompting for Zero-Shot Knowledge Graph
Question Answering”. In: Proceedings of the 1st Workshop on
Natural Language Reasoning and Structured Explanations
(NLRSE). Association for Computational Linguistics, 2023,
pp. 78–106.
[2] Shaoxiong Ji, Shirui Pan, et al. “A Survey on Knowledge
Graphs: Representation, Acquisition, and Applications”. In:
IEEE Transactions on Neural Networks and Learning Systems
(2022), pp. 494–514.
37 / 38

38. GNP
Conclusion
References II
[3] Bishan Yang, Scott Wen-tau Yih, et al. “Embedding Entities and
Relations for Learning and Inference in Knowledge Bases”. In:
Proceedings of the International Conference on Learning
Representations (ICLR) 2015. 2015.
[4] Michihiro Yasunaga, Antoine Bosselut, et al. “Deep
Bidirectional Language-Knowledge Graph Pretraining”. In:
Advances in Neural Information Processing Systems. 2022,
pp. 37309–37323.
[5] Xikun Zhang et al. “GreaseLM: Graph REASoning Enhanced
Language Models”. In: International Conference on Learning
Representations. 2021.
38 / 38