Documentul detaliază algoritmi de găsire a drumurilor minime în grafuri, inclusiv Kruskal, Prim, Floyd-Warshall, Bellman-Ford, Dijkstra, și A*. Fiecare algoritm are o complexitate de timp specifică, iar documentul explică modul în care se pot aplica pentru identificarea drumurilor de cost minim între vârfuri. Se oferă, de asemenea, exemple și resurse suplimentare pentru aprofundarea subiectului.

1. graf?gamedev:null
Vlad Manea, Radu Vasile Gagos
{vlad.manea, radu.gagos}@info.uaic.ro
Clubul dezvoltatorilor de jocuri «FII Gamedev»
Microsoft Student Partners

2. Salut

3. Arbori parțiali de cost minim
Kruskal • Prim
Drum minim de sursă multiplă
Floyd Warshall = Roy Floyd
Drum (minim) de sursă unică
Bellman Ford • Dijkstra • A* Search
Cuprins

4. Mulțimea (setul) de vârfuri V
pot fi etichetate de la 1 la N.
Mulțimea de arce E
inclusă în mulțimea ordonată V2
,
pot fi etichetate de la 1 la M.
Funcția de cost
are forma f: E → ℝ.
Graful G = (V, E)
7.3

5. Graf orientat
ordinea vârfurilor din (i, j) ∊ E contează.
Graf neorientat
arc = muchie și dacă (i, j) ∊ E, atunci (j, i) ∊ E.
Componentă conexă
subset maximal al lui V cu vârfuri conectate,
G conex dacă are o singură componentă.
Tipuri de grafuri

6. Exemplu
de
graf

7. Graf neorientat conex aciclic
are M = N – 1 muchii.
Arbore parțial al unui graf conex G = (V, E)
arbore care conține toată mulțimea V.
Arbore parțial de cost minim (APM)
are suma costurilor muchiilor minimă
în raport cu cei M
N−1
arbori parțiali.
Arbore

8. Arbore parțial

9. Arbore parțial

10. Arbore parțial

11. APM-Generic(G, f)
1. A ⟵ ∅
2. cât timp A nu este APM execută
3. găsește (u, v) ∊ E sigură pentru A
4. A ⟵ A ∪ {(u, v)}
5. întoarce A
Pasul 3 este cel mai dificil
algoritmii Kruskal și Prim îl implementează.
Arbore parțial de cost minim

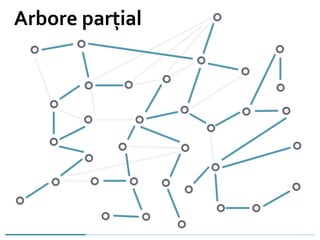
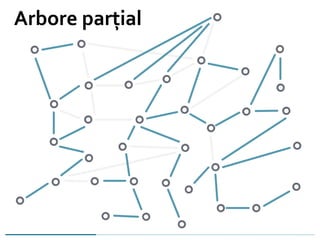
12. APM-Kruskal(G, f)
1. A ⟵ ∅
2. pentru v ∊ V execută
3. Formează-Set(v)
3. Sortează muchiile din E după costurile f
4. pentru (u, v) ∊ E execută
5. dacă Găsește-Set(u) ≠ Găsește-Set(v) atunci
6. A ⟵ A ∪ {(u, v)}
7. Unește(u, v)
8. întoarce A
Demonstrații de corectitudine în [1][2]
APM-Kruskal

13. Se sortează E cu un algoritm rapid
în complexitatea timp O(M × log(M)).
Operațiile de Uniune-Găsire
se realizează cu păduri de mulțimi disjuncte
Iar complexitatea timp este O(M × α(M, N)).
Întreg algoritmul
are complexitatea timp O(M × log(M)).
APM-Kruskal

14. Exemple
preluate din [2]
APM-Kruskal
1
2 3 5 6
4
9 5 3 1
2
7 3 1
1 43 6
5
2
34
5
5681
80
44
62

15. APM-Prim(G, f , r)
1. Q ⟵ V
2. pentru u ∊ Q execută
3. distanță[u] ⟵ ∞
4. distanță[r] ⟵ 0
5. tată[r] ⟵ NIL
6. cât timp Q ≠ ∅ execută
7. u ⟵ Extrage-Min(Q)
8. pentru v ∊ {w | (u, w) ∊ E} execută
9. dacă v ∊ Q și f(u, v) < distanță[v] atunci
7. tată[v] ⟵ u
8. distanță[v] ⟵ f(u, v)
9. Actualizează-Min(Q, v, distanță[v])
APM-Prim

16. Operațiile Extrage-Min și Actualizează-Min
sunt implementate cu ajutorul unui heap/set,
complexitatea timp totală e O(M × log(N)).
Întreg algoritmul
are complexitatea timp O(M × log(N)),
aceeași cu cea Kruskal deoarece M < N2.
Demonstrație de corectitudine în [1]
APM-Prim

17. APM-Prim
Exemple
preluate din [2]
1
2 3 5 6
4
9 5 3 1
2
7 3 1
1 43 6
5
2
34
5
5681
80
44
62

18. Drum
Secvență de arce din E.
Costul unui drum
este suma costurilor arcelor lui.
Drum (de cost) minim de la u la v
orice alt drum de la u la v are un cost
mai mare sau egal cu costul lui.
Drum de cost minim

19. Enunțarea problemei
Să se găsească drumul de cost minim între
oricare două vârfuri din V.
Soluția prin programare dinamică
Se poate demonstra [3] că un drum de cost
minim de la u la w este concatenarea a două
drumuri de cost minim: un drum de cost
minim de la u la v și unul de la v la w.
Drum minim de sursă multiplă

20. DM-Floyd-Warshall
DM-Floyd-Warshall(A)
1. D ⟵ A
2. pentru k ⟵ 1, N execută
3. pentru i ⟵ 1, N execută
4. pentru j ⟵ 1, N execută
5. Dij = min(Dij, Dik + Dkj)
6. întoarce D
Demonstrații de corectitudine în [1][3]

21. Ordinea <k, i, j> este importantă
Între i și j apar intermediari doar din {1, …, k}.
Întreg algoritmul
are complexitatea timp O(N3).
Algoritmul poate fi modificat
pentru a calcula și un drum de cost minim,
pentru a calcula închiderea tranzitivă a lui G.
DM-Floyd-Warshall

22. Enunțarea problemei
Să se găsească drumul de cost minim între
un vârf sursă u și oricare vârf din V.
Soluția prin greedy
Vom presupune pentru simplitate că funcția
f: E → ℝ₊. Fiecare vârf este apropiat cât mai
mult de sursă în unul sau mai mulți pași.
Vârful cel mai apropiat este ales greedy.
Drum minim de sursă unică

23. DM-Bellman-Ford(G, f , s)
01. pentru u ∊ V execută
02. distanță[u] ⟵ ∞
03. distanță[s] ⟵ 0
04. tată[s] ⟵ NIL
05. Q ⟵ s
06. cât timp Q ≠ ∅ execută
07. u ⟵ Pop-Coadă(Q)
08. pentru v ∊ {w | (u, w) ∊ E} execută
09. dacă distanță[v] > distanță[u] + f(u, v) atunci
10. distanță[v] ⟵ distanță[u] + f(u, v)
11. tată[v] ⟵ u
12. Push-Coadă(Q, v)
DM-Bellman-Ford

24. Operațiile Pop-Coadă și Push-Coadă
necesită timp constant,
deci au complexitatea timp constant O(1).
Întreg algoritmul
are complexitatea timp O(M × N),
dar în practică se comportă foarte bine.
Demonstrație de corectitudine în [1]
DM-Bellman-Ford

25. DM-Bellman-Ford
Exemple
preluate din [2]
1 2
1 43 6
5
2
34
5
5681
80
44
62
45
3
6 7
2
3
8
10
2
4
7
1
20 2
3
1
2 3 5 6
4
9 5 3 1
2
7 3 1

26. DM-Dijkstra
DM-Dijkstra(G, f , s)
01. pentru u ∊ V execută
02. distanță[u] ⟵ ∞
03. distanță[s] ⟵ 0
04. tată[s] ⟵ NIL
05. S ⟵ ∅
06. Q ⟵ V
07. cât timp Q ≠ ∅ execută
08. u ⟵ Extrage-Min(Q)
09. S ⟵ S ∪ {u}
10. pentru v ∊ {w | (u, w) ∊ E} execută
11. dacă distanță[v] > distanță[u] + f(u, v) atunci
12. distanță[v] ⟵ distanță[u] + f(u, v)
13. Actualizează-Distanță(Q, v, distanță[v])
14. tată[v] ⟵ u

27. Actualizează-Distanță și Extrage-Min
sunt implementate cu ajutorul unui heap/set;
complexitatea timp totală e O(N × log(N)).
Algoritmul Dijkstra
are complexitatea timp O((M + N) × log(N)),
deoarece fiecare muchie poate actualiza Q.
Demonstrație de corectitudine în [1]
DM-Dijkstra

28. DM-Dijkstra
Exemple
preluate din [2]
1 2
1 43 6
5
2
34
5
5681
80
44
62
45
3
6 7
2
3
8
10
2
4
7
1
20 2
3
1
2 3 5 6
4
9 5 3 1
2
7 3 1

29. Enunțarea problemei
Găsiți rapid un drum de cost aproape minim
între un vârf sursă u și un vârf v.
Soluția prin euristică
Dacă estimăm drumul spre destinație, atunci
vârfurile mai apropiate au șanse mai mari.
Fie estimatorul e: V → ℝ₊, care se adaugă la
distanță, obținându-se criteriul distanță*.
Drum minim de sursă unică

30. DM-A*-Search
DM-A*-Search (G, f , e, s)
01. pentru u ∊ V execută
02. distanță[u] ⟵ ∞
03. distanță[s] ⟵ 0
04. tată[s] ⟵ NIL
05. S ⟵ ∅
06. Q ⟵ V
07. cât timp Q ≠ ∅ execută
08. u ⟵ Extrage-Min*(Q)
09. S ⟵ S ∪ {u}
10. pentru v ∊ {w | (u, w) ∊ E} execută
11. dacă distanță[v] > distanță[u] + f(u, v) atunci
12. tată[v] ⟵ u
13. distanță[v] ⟵ distanță[u] + f(u, v)
14. Actualizează-Min*(Q, v, distanță*[v])

31. Operațiile Extrage-Min* și Actualizează-Min*
sunt implementate cu ajutorul unui heap/set,
deci complexitatea timp a uneia e O(log(N)).
Întreg algoritmul
poate avea complexitate exponențială,
dar în practică se comportă excelent!
Exemple pe internet
DM-A*-Search

32. Lecții
http://en.wikipedia.org/wiki/Pathfinding
http://www.policyalmanac.org/games/aStarTutorial.htm
http://theory.stanford.edu/~amitp/GameProgramming/
Demo
http://links.math.rpi.edu/applets/appindex/graphtheory.html
http://www.unf.edu/~wkloster/foundations/DijkstraApplet/DijkstraApplet.htm
http://jung.sourceforge.net/applet/shortestpath.html
Cărți
[1] Thomas Cormen, Charles Leiserson, Ronald Rivest, Introducere în algoritmi, Agora 2000
[2] Emanuela Cerchez, Marinel Șerban, Programarea în limbajul C/C++ pentru liceu •••, Polirom 2006
[3] Dorel Lucanu, Mitică Craus, Proiectarea algoritmilor, Polirom 2008
Referințe

33. Mulțumim:)
Vlad Manea, Radu Vasile Gagos
{vlad.manea, radu.gagos}@info.uaic.ro