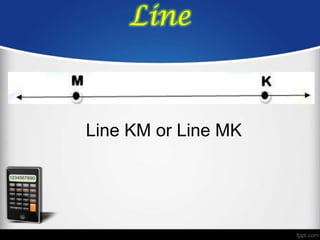
1. Geometry originated from early peoples' use of measurement to build structures, and was later formalized by Euclid who developed a logical system of geometry in his work The Elements. 2. Euclid's geometry, known as Euclidean geometry, is based on logical reasoning of relationships in flat, two-dimensional surfaces known as planes. 3. Geometry studies properties of shapes, sizes, positions, and space through concepts like points, lines, and planes.

2. Geometry means earth measurement. Early peoples
used their knowledge of geometry to build
roads, temples, pyramids, and irrigation systems. The
more formal study of geometry today is based on an
interest in logical reasoning and relationships rather
than in measurement alone. Euclid (300 b.c.) organized
Greek geometry into a thirteen-volume set of books
named The Elements, in which the geometric
relationships were derived through deductive reasoning.
Thus, the formal geometry studied today is often called
Euclidean geometry. This geometry is also called plane
geometry because the relationships deal with flat
surfaces.

3. •come from two Greek words:
“geo” which means “Earth” and
“metron” and which means
“Measure”

4. •is a branch of mathematics concerned
with questions of shape, size, relative
position of figures, and the properties of
space

5. •was extremely important to ancient
societies and was used for
surveying, astronomy, navigation,
and building

6. Geometer
•is the mathematician who
works in the field of
geometry

7. UNDEFINED TERMS
•are concepts where Geometry
and other Mathematical System
are based
•are terms that are accepted
without definition

8. Point
•may be described as a location with no
length, no width, and no depth
•is usually represented by a small dot
•is always named with a capital letter
Point A

9. Line
•may be described as a set of points
going straight on forever in two
opposite directions
•is a infinite set of points that has
length, but no width and depth
•is usually represented by a straight
line with two arrowheads to indicate
that the line extends without end in two
directions

10. Line
•is usually named in one of two ways
like the line containing points K and M
may be named by either:
1. Using any two (never more than two) points on
the line with a line indicator above the points, for
example KM or MK, the line indicator above the
capital letters always points horizontally from side
to side and never any other direction: it is the
actual location of the points in space that
determines the location and direction of the line
indicator above the capital letters in the notation

11. Line
Line KM or Line MK

12. Line
2. By using the lower case script letter l with
number subscript (or any lower case
letter), for example: l1 or k
l1 or k

13. Plane
•may be described as a set of points going
on forever in all directions except any
direction that creates depth
•have length and width, but no depth
•cannot be drawn but usually represented
as parallelograms, either with the arrows
indicating that the points go on forever or
without the arrows even though the points
do go on forever

14. Plane
•is simply referred to as “plane m” or “plane
ABC (any 3 points on the plane that are not
on the same line)” or “ the plane
containing…(whatever pertains to the
discussion)”

15. DEFINITION
Concepts in Geometry will be
defined by using the three undefined
terms and/or other terms that have
already been defined.

16. Definition
1. A good definition should contain
ordinary words and geometric terms
that have been previously defined or
accepted as undefined
2. A good definition should list only the
essential properties of the term being
defined
3. A good definition is reversible

17. POSTULATE
- is a statement which is
accepted as true without
proof

18. THEOREM
- is a statement that
needs to be proved

19. COROLLARY
- is a direct consequence
of another theorem

20. Assignment:
1. Draw a figure and identify
points, lines and planes in the
figure drawn.
2. Study the postulates and
theorems regarding points,
lines and planes.
3. What are the subsets of a
line?