Download to read offline
Uploaded byCarlos Gavidia-Calderon
Game-theoretic Analysis of Development Practices: Challenges and Opportunities
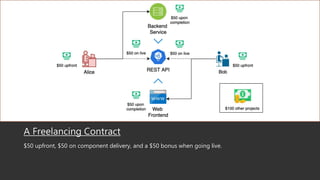
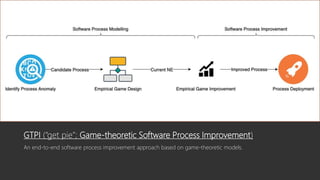
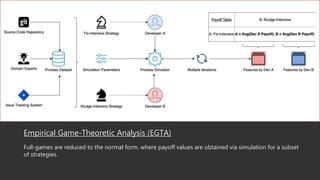
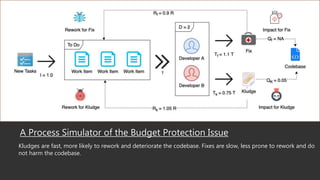
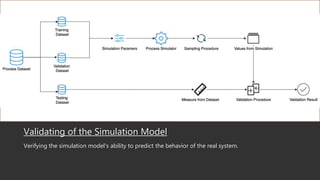
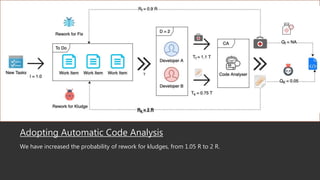
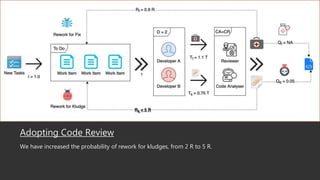
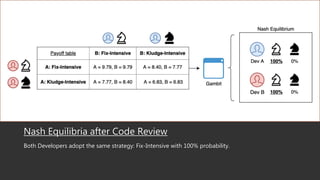
This document summarizes a research paper that uses game theory to analyze software development practices and processes. It describes how game theory can model conflicts and cooperation between decision makers. It then discusses several software development dilemmas, such as a freelancer's dilemma over work quality and a team's dilemma over quick fixes versus proper long term solutions. The researchers built simulation models of these dilemmas and analyzed how different development practices, like code reviews, affect the optimal strategies and outcomes. Their goal is to apply game theory to improve software processes and practices.
More Related Content
Similar to Game-theoretic Analysis of Development Practices: Challenges and Opportunities
Game-theoretic Analysis of Development Practices: Challenges and Opportunities
- 1. Game-Theoretic Analysis of DevelopmentPractices: Challenges and Opportunities Carlos Gavidia-Calderon, Federica Sarro, Mark Harman and Earl T. Barr The Journal of Systems and Software, 2019
- 2. "All the reallystressful times for me have been about process. They haven't been about code. When code doesn't work, that can actually be exciting. Process problems are a pain in the ***. You never, ever want to have process problems ... That's when people start getting really angry at each other.” Linus Torvalds (from The Register)
- 3. Roger Myerson. 2007Nobel Memorial Prize in Economic Sciences) “Game theory can be defined as the study of mathematical models of conflict and cooperation between intelligent rational decision- makers.”
- 4. A Freelancing Contract $50upfront, $50 on component delivery, and a $50 bonus when going live.
- 5. The Freelancer’s Dilemma Althoughmutual cooperation is preferred, the freelancer’s end working individually.
- 6. GTPI (“get pie”;Game-theoretic Software Process Improvement) An end-to-end software process improvement approach based on game-theoretic models.
- 7. The Budget ProtectionIssue “(The) software item was in dire need of a fix. … a fix was estimated at about 20 person- days. The … team instead chose to internally develop … a cheap patch which could be done for about five person-days”
- 8. Empirical Game-Theoretic Analysis(EGTA) Full-games are reduced to the normal form, where payoff values are obtained via simulation for a subset of strategies.
- 9. A Process Simulatorof the Budget Protection Issue Kludges are fast, more likely to rework and deteriorate the codebase. Fixes are slow, less prone to rework and do not harm the codebase.
- 10. Validating of theSimulation Model Verifying the simulation model’s ability to predict the behavior of the real system.
- 11. Current Nash Equilibrium BothDevelopers adopt the same strategy: Kludge-Intensive with 100% probability.
- 12. Adopting Automatic CodeAnalysis We have increased the probability of rework for kludges, from 1.05 R to 2 R.
- 13. Nash Equilibria afterAutomatic Code Analysis In 2 out of 3 equilibria, the kludge-intensive behavior has a significant probability.
- 14. Adopting Code Review Wehave increased the probability of rework for kludges, from 2 R to 5 R.
- 15. Nash Equilibria afterCode Review Both Developers adopt the same strategy: Fix-Intensive with 100% probability.
- 16. The Assessor's Dilemma: ImprovingBug Repair via Empirical Game Theory Carlos Gavidia-Calderon, Federica Sarro, Mark Harman and Earl T. Barr IEEE Transactions on Software Engineering 2019
Editor's Notes
- #2 My name is Carlos Gavidia. I recently graduated as PhD. in Software Engineering from University College London, under the supervision of Earl Barr, Federica Sarro and Mark Harman. Today, I'll be presenting the paper we published in the "New Trends and Ideas" track of the Journal of Systems and Software.
- #3 Software needs to scale to support an increasing number of users; and software development processes need to scale to support large distributed teams, operating over complex codebases. Let's take the Linux kernel as an example: it has more than 13 000 contributors since 2015, adding around 10 000 lines of code daily. When operating at this scale, process problems can take precedence over technical ones, as seen in this quote from Linus Torvalds. The most widely adopted software processes come from the practitioner community, and are based on decades of software engineering experience. In our paper, we complement this empirical approach by including mathematical models in the process improvement effort.
- #4 When we mention mathematical models, we are referring specifically to game-theoretic ones. Roger Myerson, in the slide, defines game theory as the "study of mathematical models of conflict and cooperation". It deals with scenarios where rational-self-interested agents interact, and these interactions affect the agent’s welfare. In game theory, these scenarios are called games, and the agents are called players. The game definition applies to card games, like poker, but also to financial markets and international relations. Game theory can help us understand, and even predict, how players would behave when engaging in a game.
- #5 Let's use an example to show how to apply game theory to a software development context. An organisation hires two freelance developers to build a software system. Bob, who is in charge of developing the web frontend, and Alice, who needs to develop the backend service. They both receive $50 upfront, and an additional $50 when they deliver their component. For the system to be finished the organisation also needs a REST API that manages communication between the backend and the frontend. The development of this API requires the expertise of both Bob and Alice. When the API is ready, both developers would receive a bonus of 50$. Also, if either Bob and Alice have time, they can pursue additional freelancing contracts for a value of $100.
- #6 Now let's build a game-theoretic model of this scenario. We consider Alice and Bob as the players. For the sake of simplicity, let's limit the actions they can perform to: 1) cooperate, represented by an upwards arrow, and 2) to not cooperate, represented by a downwards arrow. In this game, by cooperation we mean a disposition to work together. The payoff table in this slide contains the payoff per player given the actions they perform. For example, the top-left cell corresponds to the scenario where Alice and Bob cooperate. In that case, the system goes live and each receive $150. When neither cooperate, in the bottom-right cell, they deliver their corresponding component without finishing the integration via the API, so each receive $100. When one freelancer cooperates but the other doesn't, the cooperating developer is not able to finish their component obtaining only the initial $50, while the non-cooperating developer finishes their component and even has time to take an additional contract, pocketing $200. Behaviour in game-theoretic models is defined in terms of strategies, where a strategy assigns a probability to each action. Game theory provides insights on how rational players would behave in a game. At an optimal outcome, players adopt a strategy such that there are no incentives for deviating. We can obtain that outcome, also called the Nash Equilibrium, processing the payoff table with an equilibrium algorithm. For this example, at equilibrium both Alice and Bob adopt the same strategy: to not cooperate with a probability of 100%. At equilibrium, both freelancers obtain $100 with no incentives for deviation, since moving to cooperation would diminish their earnings in $50. This outcome is not good for the organisation, since the system is not finished. It is also not good for the freelancers. If both cooperate, besides a happy client they obtain more money. That's the dilemma behind this freelancer game: although the organisation, and the freelancers, would be in a better position if they cooperate, the software process behind the contract forces them to abandon cooperation.
- #7 We believe that many software processes suffer from a similar problem, converging towards unwanted behaviour at equilibrium. To address this issue, in our paper we propose GTPI: a software process improvement approach based on game-theoretic models. GTPI stands for game-theoretic process improvement and is composed of 4 steps. In the first one, we identify a process anomaly, like the freelancers not cooperating. In step 2, we built a game-theoretic model of the process to improve, like the payoff table in the previous slide. Having the model ready, we can obtain its Nash equilibrium and see if it matches the process anomaly identified in step one. If that is the case, in step 3 we can use the game-theoretic model to experiment with process interventions. Once we have found an adequate process intervention, meaning its model shows the desired behaviour at equilibrium, we proceed to the last step of GTPI and deploy and adopt the improved process.
- #8 Next, let's explore how to use GTPI by addressing a software process problem reported by Lavallée and Robillard in their ICSE 2015 paper. In their paper, they describe a development team that found a problem in a software system. Building a permanent fix for this problem would take 20-person days, but building a temporal workaround would demand 5 person-days. To avoid going over budget, this team opted for the workaround. The authors found that 12 other teams have faced the same problem before, and all those teams also choose for the workaround instead of the permanent fix. This scenario, which the author’s called the budget protection issue, is problematic since developing a permanent fix is cheaper than developing 12 workarounds.
- #9 Now that in step 1 we have identified a process anomaly, the budget protection issue, we can move to the empirical game design step. Game representations, like the payoff table, grow exponentially in size with the number of actions and players. In the Lavallee and Robillard paper, they observed 45 people distributed in 13 teams for around 10 months, so we need abstraction to keep a manageable game size. To this purpose, we propose to adopt Empirical Game-Theoretic Analysis, or EGTA. The reduced games produced by EGTA are also payoff tables, with the payoff values obtained via simulation. In EGTA models, the actions are limited to a set of strategies of interest. For our model of the budget protection issue, we consider the two developers as players, with a payoff as the number of features delivered per release. Our model has only two strategies: 1) in a fix-intensive strategy, developers commit proper fixes until a week before the release, when they switch to commit kludges, or workarounds and 2) a kludge-intensive strategy, where a developer switch to committing kludges when work items start accumulating. In the slide, for the table cell corresponding to a fix-intensive strategy against a kludge-intensive strategy, we use the process simulator to obtain the number of features delivered per developer. Over multiple iterations so we can calculate the averages. We select these two strategies arbitrarily for demonstration purposes. In a real setting, they should come from a dataset of the process to model. Building a process dataset is not trivial, considering that data might just not be there. For the budget protection issue, the code repository can be a source of commit behaviour. But then we would need a way to differentiate commits for proper fixes from commits for kludges. As a proxy, we can use a static analysis tool like FindBugs over commits. We can even apply NLP techniques to code review comments, or just ask the Tech Lead which behaviours they believe are relevant. Assembling the process dataset is an essential requisite for GTPI adoption.
- #10 Now let's review the simulation model we use to obtain payoff values. Work items arrive at a given day according to I, where they can be picked by any developer available. The time developers spend on a work item depends if they choose to address it with a fix or a kludge. We want to reflect that kludges are faster to code than fixes, so fixes take 10% more time than T, the average resolution time; while kludges take 25% less than T. We expect kludges to be more likely to require rework, like bug fixing; so their probability of rework is 5% more than R, the average rework probability. For proper fixes, this probability is 10% lower than R. Kludges have a negative impact on codebase quality, so every time a kludge is committed the average resolution time increases in 5%. In a 2016 paper by Mi and Keung, they reported in an Eclipse Platform annual release the average resolution time T is around 30 days, with an R of 7% for bug reopening. We plugged these values in the simulator when obtaining payoff values.
- #11 A step we skipped that is important when applying GTPI is simulation model validation. We need to be certain that the simulation actually reflects the process to improve. There's an extensive literature in software process simulation; here in the slide, we show one of the many validation approaches. We split the process dataset into 3 parts: training, validation and testing. We use the training dataset to obtain simulation parameters, like the values of R, T, and I. The validation dataset is used for model calibration. Let's say that, to ensure accurate payoff values, we want our simulation to predict the average number of features delivered per release. We obtain an estimate from the simulation model and compare it with the features released in the validation dataset. If they do not match, we would then need to improve the simulation design. We use the testing dataset for a final verification: using the simulation we obtain multiple samples of a target measure, like the number of features, and then compare if they match what’s observed in the testing dataset. This comparison can be done via hypothesis testing, confidence intervals or even expert opinion.
- #12 When the simulation model is ready, we can use it to populate the payoff table. After feeding the payoff table to a game solver like Gambit, we see that, at equilibrium, both developers do the same: to adopt the kludge-intensive strategy with 100% probability, matching what was reported by Lavallee and Robillard. We see that this payoff table shares similarities with the model generated for the freelancer's dilemma. Both developers would deliver more features if they adopted the fix-intensive strategy, but this strategy is absent at equilibrium.
- #13 Now that we confirmed the software process anomaly, we can move the third step of GTPI. We will use the game-theoretic model to explore potential solutions. An initial attempt would be to make kludges more expensive by making them more likely to require rework. We can try adopting post-commit analysis with an automatic tool like FindBugs, that can detect problematic code. Let's assume that adopting such a tool would increase the rework probability for kludges, from 1.05 R to 2 R.
- #14 We built a new payoff table using the updated simulation model and used Gambit to obtain the behaviour at equilibrium. Payoff values show the kludge-intensive strategy is now producing fewer features per release. Now we have 3 equilibria instead of 1: while in one we have a 100% probability for the fix-intensive strategy, as desired, in the other two the kludge-intensive strategy is still very dominant. Adopting automatic code analysis is beneficial, but we believe we can do better.
- #15 Given the promising results obtained by increasing the cost of kludges, let's try to go a bit further. If besides automatic code analysis we include a code review made by an actual engineer, let's assume the probability of rework for kludges increases from 2 R to 5 R.
- #16 Here's the new payoff table using the updated simulation model. The equilibrium obtained is now aligned with what the organisation wants: both developers adopt the fix-intensive strategy with a probability of 100%. Also, while in the original process we obtained 18.12 features per release, in the new process at equilibrium we are delivering 19.58 features, an increase of 8% while keeping a healthy codebase. After evaluating this candidate process in the model, we now have some confidence to actually deploy it to the team.
- #17 In our JSS paper the goal was to introduce GTPI and show how we use game-theory to reason formally about software processes. In a later publication in the Transactions on Software Engineering, we use GTPI to improve the prioritisation of software tasks. Using game-theoretic models, we show that industry practices like bug triage are not effective, and we propose a new reputation-based process with truthful prioritisation at equilibrium. If you're interested in this topic, please read this work.
- #18 Besides the budget-protection issue and task prioritisation, we believe there are many other process problems that can be tackled with game-theory. We invite you to use GTPI to improve software processes at your organisation. Thank you very much for your time, and now I'm ready for questions.