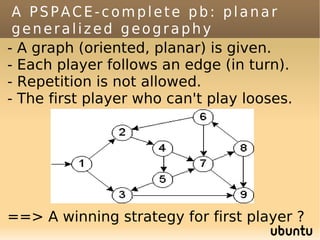
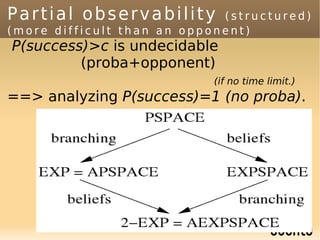
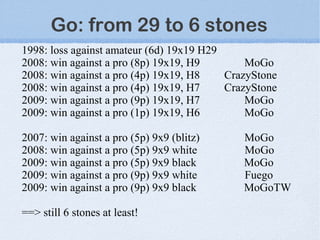
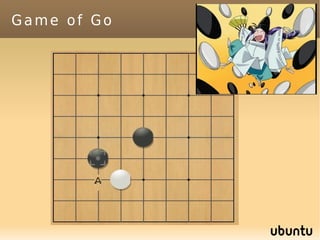
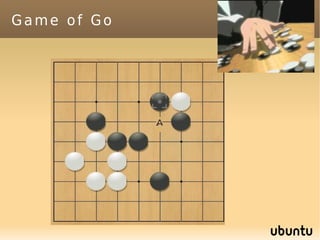
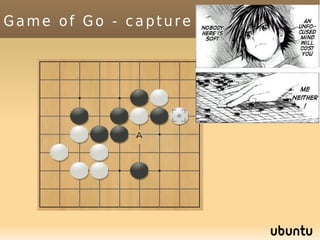
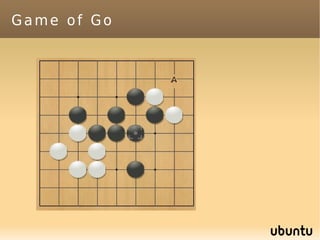
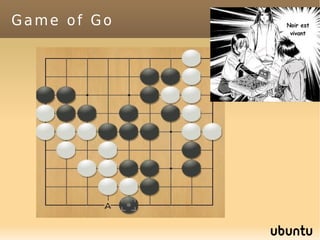
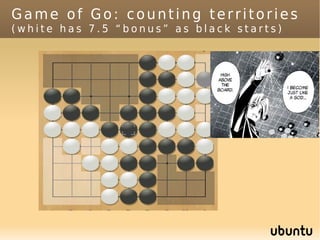
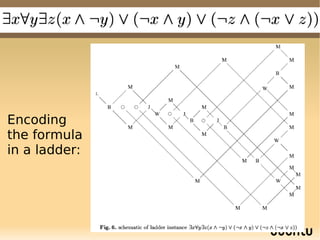
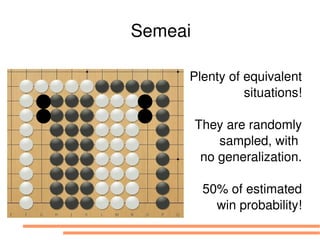
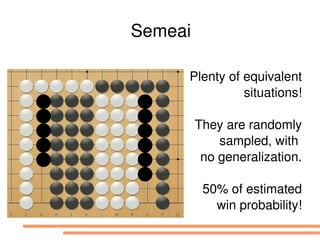
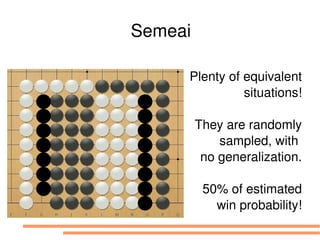
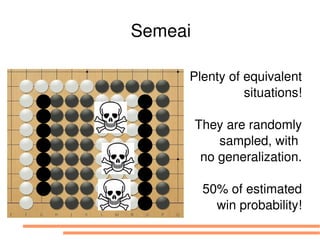
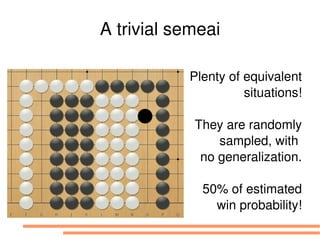
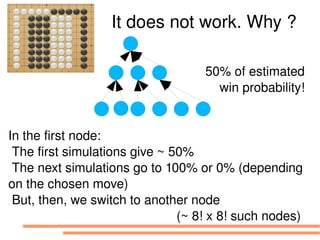
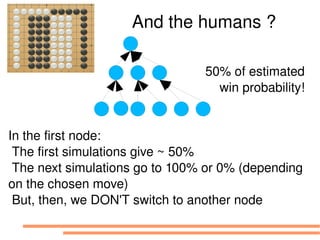
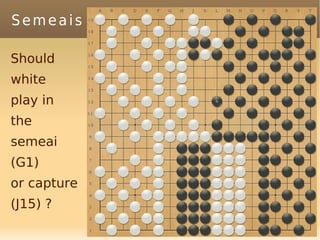
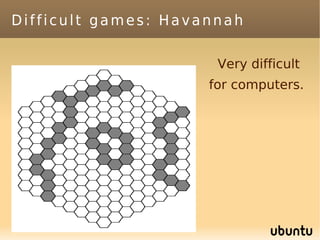
The document discusses bandit-based Monte Carlo planning, focusing on games such as Go, and explores complexity measures, computational complexity, and various game types including partially observable games. It highlights the evolution of AI performance in games like draughts and chess, the intricacies of decision-making in complex game scenarios, and the relationship between game complexity and human versus machine competition. The work also contemplates ongoing challenges for Monte Carlo Tree Search (MCTS) methods in handling large and partially observable game environments.

1. Bandit-based Monte-Carlo planning: the game
of Go and beyond
Games
Olivier.Teytaud@inria.fr + too many people for being all cited. Includes Inria, Cnrs, Univ.
Paris-Sud, LRI, CMAP, Univ. Amsterdam, Taiwan universities (including NUTN)
TAO, Inria-Saclay IDF, Cnrs 8623, Lri, Univ. Paris-Sud,
Digiteo Labs, Pascal Network of Excellence.
Tao,
January 2010+updated 2012.

2. Games
Introduction
Complexity measures
Computational complexity
Partial observability
Zoology

3. Introduction to games
Partially or fully observable
(“phantom” games)
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

4. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

5. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not (reputation)
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

6. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

7. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not
(rengo)

8. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

9. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

10. Introduction to games
Partially or fully observable
Randomized or not
Iterated or not
1,2,3,... players
Decentralized or not
Continuous or not
Infinite time or not

11. Games
Introduction
Complexity measures
Computational complexity
Partial observability
Zoology

12. Complexity measures
(not always well defined)
State-space complexity
Game-tree size
Decision complexity
Game-tree complexity
Computational complexity
Perfect-play complexity
State of the art level

13. Complexity measures
(not always well defined)
State-space complexity = number
of possible states
Game-tree size
Decision complexity
Game-tree complexity
Computational complexity
Perfect-play complexity
State of the art level

14. Complexity measures
(not always well defined)
State-space complexity
Game-tree size = number of leafs
Decision complexity
Game-tree complexity
Computational complexity
Perfect-play complexity
State of the art level

15. Complexity measures
(not always well defined)
State-space complexity
Game-tree size
Decision complexity = min # of
leafs of tree showing perfect play
Game-tree complexity
Computational complexity
Perfect-play complexity
State of the art level

16. Complexity measures
(not always well defined)
State-space complexity
Game-tree size
Decision complexity
Game-tree complexity = # of leafs
for perfect play with constant depth
Computational complexity
Perfect-play complexity
State of the art level

17. Complexity measures
(not always well defined)
State-space complexity
Game-tree size
Decision complexity
Game-tree complexity
Computational complexity (=
complexity classes, later)
Perfect-play complexity
State of the art level

18. Complexity measures
(not always well defined)
State-space complexity
Game-tree size
Decision complexity
Game-tree complexity
Computational complexity
Perfect-play complexity (complexity
of perfect algorithm)
State of the art level

19. Complexity measures
(not always well defined)
State-space complexity
Game-tree size
Decision complexity
Game-tree complexity
Computational complexity
Perfect-play complexity
State of the art level

20. State of the art level
Very weak solving
Means that we know who should win
Typically proved by strategy-stealing
E.g.: hex (first player wins), hex + swap
(second player wins)
Weak solving
Strong solving
Best results so far

21. State of the art
level
Very weak solving
Weak solving
Perfect play reached with reasonnable computation
time
Biggest success: draughts (tenths of years of
computation on tenths of machines)
Strong solving
Best results so far

22. State of the art
level
Very weak solving
Weak solving
Strong solving
Perfect play from any situation in
reasonable time (variants of Tic-Tac-Toe)
Best results so far

23. State of the art level
Very weak solving
Weak solving
Strong solving
Best results so far
Shi-Fu-Mi: humans loose
English draughts: humans + machines reach perfect
play
Chess: nobody can compete with machines
9x9 Go: MoGoTW won with the disadvantageous side
with a top player

24. Games
Introduction
Complexity measures
Computational
complexity
Partial observability
Zoology

25. Computational complexity:
Main reasons for this measure ?
Good feeling of understanding
(disagree if you want :-) )
Explicit families of problems
(extracted by reduction)
Fun
Connections
with classical complexity measures
Much better for looking clever
(when you speak about NP-complete
problems you look clever)

26. Computational complexity:
Drawbacks
Not clearly related to human/computer
comparisons
Trivial games can be very complex (this
measure if a worst case on situations that might never
occur from the start of the game - many solvings are
based on openings restricting the game)
Often based on incredibly long games

27. Computational complexity
Known:
Conjectured: strict inclusions everywhere.
Higher classes include undecidable cases.

28. Computational complexity
Given a class X, a problem q can be
in X
or harder than pbs in X (X-hard)
or both (X-complete)
or neither
NP
NP -difficile
NP -complete

29. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
solved, even with infinite time and
space ?

30. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are The existence of exponential problems is known.
No. there problems solvable in
exponential time but not in polynomial
It means (roughly) “polynomial with a machine which
time ?
can run several branches simultaneously”.
Are there problems solvable in
It means (very roughly) “polynomial in linear time ?
quadratic time but not with a machine which
just has to verify a proof”.
Are there problems which can't be
solved, even with infinite time and
Maybe P = NP is not so interesting as a question :-)
space ?

31. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
solved, even with infinite time and
space ?

32. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
No.
time ? are intermediate problems (if P≠ NP).
There
Are there problems solvable in
quadratic time butNP-problems
Yet, many important not in linear time ?
Are are eitherproblems which can't be
there P or NP-complete.
solved, even with infinite time and
space ?

33. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
solved, even with infinite time and
space ?

34. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
YES, infinite time and
solved, even with YES, and YES.
space ?

35. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
solved, even with infinite time and
space ?

36. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
YES !
solved, even with infinite time and
All P problems do not have
space ? the same complexity.

37. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
Are there problems solvable in
exponential time but not in polynomial
time ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
solved, even with infinite time and
space ?

38. Complexity quizz
NP means non-polynomial ?
Assume P≠ NP. NP=NP-complete U P ?
YES ! Undecidable problem.
Are there problems solvable in
E.g.: time but not in polynomial
exponential
time ? Is there a seg-fault ?
Are there problems solvable in
quadratic time but not in linear time ?
Are there problems which can't be
solved, even with infinite time and
space ?

39. Computational complexity
For evaluating the complexity of your game:
1. Generalize your game to any size
(non trivial for chess)
2. Consider the problem:
- here is a board
- is the situation a win in perfect play ?
NP
NP
NP -complete -difficile

40. How to show X-completeness
The problem is in X: show that you can
solve it with resources allowed in class X.
The problem is complete: show that you
can encode a X-complete problem in your
problem.
NP
NP
NP -complete -difficile

41. Computational complexity
==> cast into a decision problem (binary question)
==> can be used for choosing optimal move
(but not necessary)
==> trivial games can be EXPTIME-hard
==> no clear correlation with the fact that a game is difficult
for a computer (when compared to humans)
NP
NP
NP -complete -difficile

42. A PSPACE-complete pb: planar
generalized geography
- A graph (oriented, planar) is given.
- Each player follows an edge (in turn).
- Repetition is not allowed.
- The first player who can't play looses.
==> A winning strategy for first player ?

43. Another PSPACE-complete pb:
quantified boolean formula
True or false ?

44. A EXPTIME-complete pb: does a
Turing machine halts in n steps ?
- A program is given.
- A number n is given.
- Will the program halt in n time steps ?
Best solution: simulate.
Cost: n (which is exponential in log(n)!)

45. Games
Introduction
Complexity measures
Computational complexity
Partial observability
Zoology

46. Partial observability
Here discussed in the compact case
(i.e. representation by formula)
Usually, compact ==> bigger cost
(e.g. P ==> PSPACE)

47. Partial observability (structured)
(more difficult than an opponent)
P(success)>c is undecidable
(proba+opponent)
(if no time limit.)
==> analyzing P(success)=1 (no proba).

48. Phantom-games >>> POMDP
See Rintanen 03 (case with formulae).

49. Phantom-games >>> POMDP
See Rintanen 03 (case with formulae).

50. Phantom-games >>> POMDP
See Rintanen 03 (case with formulae).

51. Phantom-games >>> POMDP
See Rintanen 03 (case with formulae).

52. Phantom-games >>> POMDP
See Rintanen 03 (case with formulae).

53. Phantom-games & POMDP
with infinite horizon
Madani et al: infinite time POMDP are
undecidable.
Auger, Teytaud: finite time deterministic
games are undecidable.
Undecidability of phantom-Go ?

54. Games
Introduction
Complexity measures
Computational complexity
Partial observability
Zoology

55. PSPACE vs EXPTIME
==> many important games are either PSPACE or EXPTIME
Theorem: If playing = filling a location
for eternity, then it is PSPACE.
(not necessarily PSPACE-complete!)
Proof: Depth-first search.
Applis: Hex, Havannah, Tic-Tac-Toe,
Atari-Go...

56. PSPACE vs EXPTIME

57. Appendix 1: the game of Go

58. Go: from 29 to 6 stones
1998: loss against amateur (6d) 19x19 H29
2008: win against a pro (8p) 19x19, H9 MoGo
2008: win against a pro (4p) 19x19, H8 CrazyStone
2008: win against a pro (4p) 19x19, H7 CrazyStone
2009: win against a pro (9p) 19x19, H7 MoGo
2009: win against a pro (1p) 19x19, H6 MoGo
2007: win against a pro (5p) 9x9 (blitz) MoGo
2008: win against a pro (5p) 9x9 white MoGo
2009: win against a pro (5p) 9x9 black MoGo
2009: win against a pro (9p) 9x9 white Fuego
2009: win against a pro (9p) 9x9 black MoGoTW
==> still 6 stones at least!

59. Game of Go (9x9 here)

60. Game of Go

61. Game of Go

62. Game of Go

63. Game of Go - capture

64. Game of Go

65. Game of Go

66. Game of Go: counting territories
(white has 7.5 “bonus” as black starts)

67. Game of Go: the rules
Black plays at the blue circle: the
white group dies (it is removed)
It's impossible to kill white (two “eyes”).
“Ko” rules: we don't come back to the same situation.
(without ko: “PSPACE hard”
with ko: “EXPTIME-complete”)
At the end, we count territories
==> black starts, so +7.5 for white.

68. NP / PSPACE / EXPTIME in Go
Tsumegos with no ko, forced moves only for
W, 2 moves for B, polynomial length: NP-
complete
Atari Go : PSPACE
Go without ko: PSPACE-hard
Go with ko + japanese rules:
EXPTIME-complete
Go with ko + superko: unknown (EXPSPACE?)
Some phantom-rengo undecidable ?
If Go with ko > Go without ko, then
PSPACE EXPTIME

69. NP / PSPACE / EXPTIME in Go
Encoding
the formula
in a ladder:

70. Appendix 2: what is difficult for
computers ? Visual things ?
70

71. Easy for computers ... because
human knowledge easy to encode.
71

72. Difficult for computers
Muy difícil para las ordenadores.
72

73. A trivial semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

74. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

75. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

76. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

77. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

78. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

79. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

80. Semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

81. A trivial semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

82. A trivial semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

83. A trivial semeai
Plenty of equivalent
situations!
They are randomly
sampled, with
no generalization.
50% of estimated
win probability!

84. It does not work. Why ?
50% of estimated
win probability!
In the first node:
The first simulations give ~ 50%
The next simulations go to 100% or 0% (depending
on the chosen move)
But, then, we switch to another node
(~ 8! x 8! such nodes)

85. And the humans ?
50% of estimated
win probability!
In the first node:
The first simulations give ~ 50%
The next simulations go to 100% or 0% (depending
on the chosen move)
But, then, we DON'T switch to another node

86. Semeais
Should
white
play in
the
semeai
(G1)
or capture
(J15) ?
86

87. Semeais
Should black
play the
semeai ?
87

88. Semeais
Should black
play the
semeai ?
88

89. Semeais
Should black
play the
semeai ?
Useless!
89

90. Difficult games: Havannah
Very difficult
for computers.

91. Conclusions + other
elements
Go complexity:
superko ?
Ishi-no-shita (captures / recaptures) ?
(more generally: characterizing strength /weakness of programs ?)
Huge complexity classes for
structured games
partially observable games (what about phantom-games ?)
decentralized games
Great results for MCTS in GGP + difficult games. Next MCTS-challenges:
Partially observable cases & large horizon : cf Cazenave, Rolet
Solve main weaknesses of MCTS
(learning the MC ? Meta-actions ? Nested MC ?
Mixing with value-function as in amazon ?)

92. Biblio
Complexity: Robson, Tromp, Taylor, Crasmaru, ...
Bandits: Lai, Robbins, Auer, Cesa-Bianchi...
UCT: Kocsis, Szepesvari, Coquelin, Munos...
MCTS (Go): Coulom, Chaslot, Fiter, Gelly, Hoock, Silver, Muller,
Pérez, Rimmel, Wang...
Tree + DP for industrial applicationl: Péret, Garcia...
Bandits with infinitely many arms:
Audibert, Coulom, Munos, Wang...
Applications far from Go: Rolet,
Teytaud (F), Rimmel, De Mesmay
...
Links with “macro-actions” ?
Parallelization, mixing with offline
learning, bias...

93. Paul Veyssière
Hassen Doghmen
Amine Bourki
Matthieu Coulm Contributors Colleagues from
NUTN and CJCU
Bandits: Lai, Robbins, Auer, Cesa-Bianchi...
UCT: Kocsis, Szepesvari, Coquelin, Munos...
MCTS (Go): Coulom, Chaslot, Fiter, Gelly, Hoock, Silver, Muller,
Pérez, Rimmel, Wang...
Tree + DP for industrial applicationl: Péret, Garcia...
Bandits with infinitely many arms:
Audibert, Coulom, Munos, Wang...
Applications far from Go: Rolet,
Teytaud (F), Rimmel, De Mesmay
...
Links with “macro-actions” ?
Parallelization, mixing with offline
learning, bias...