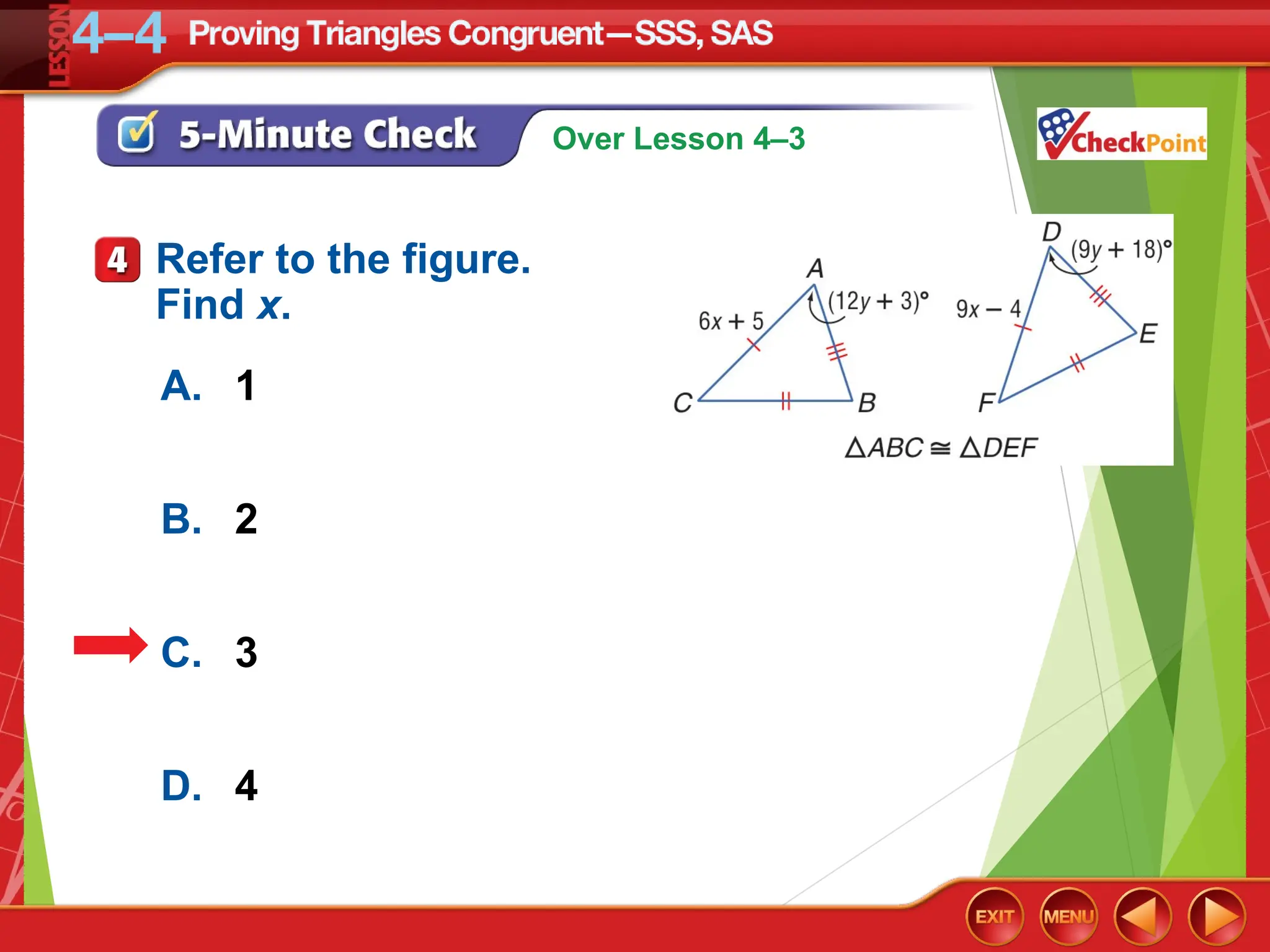
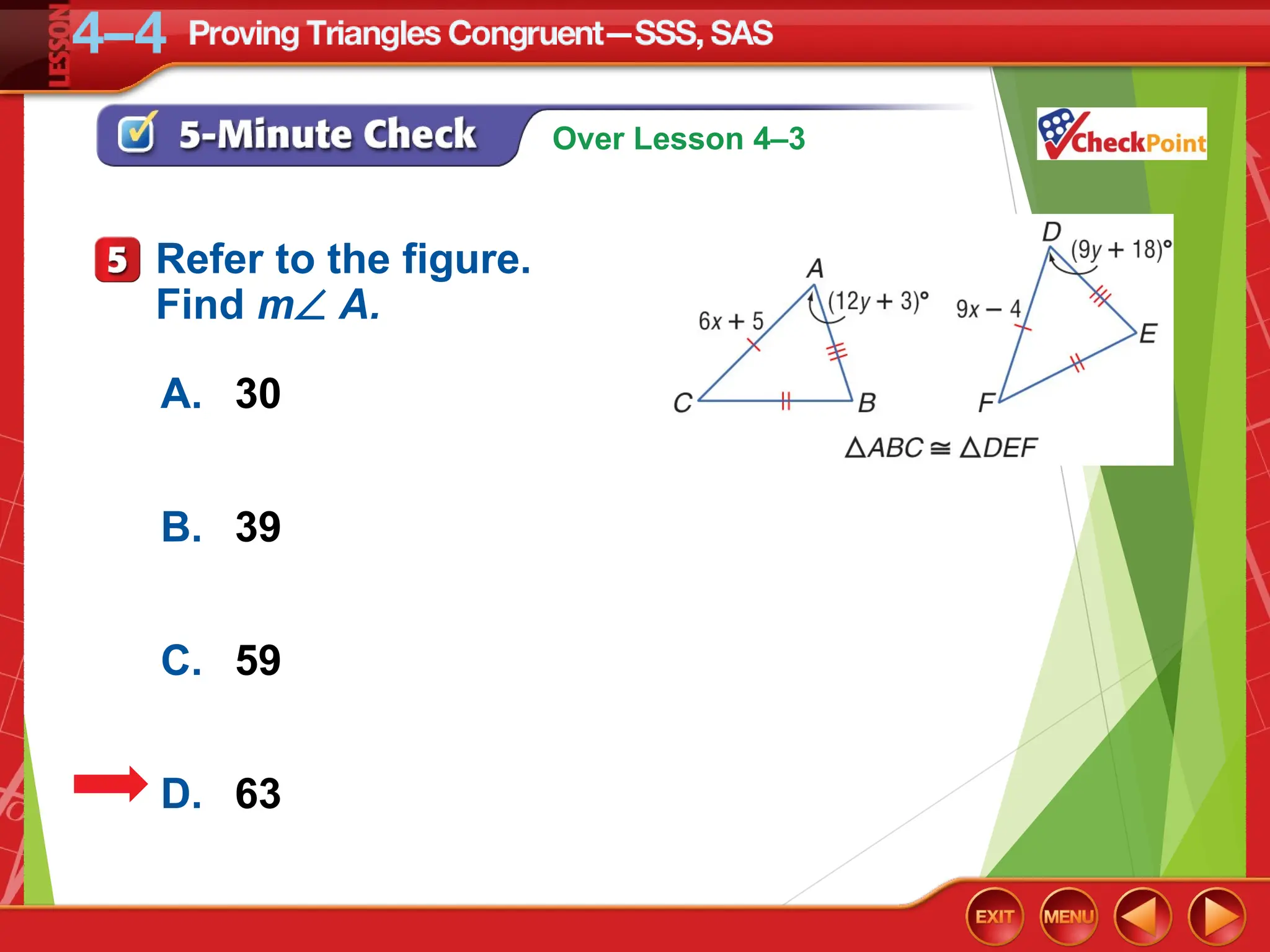
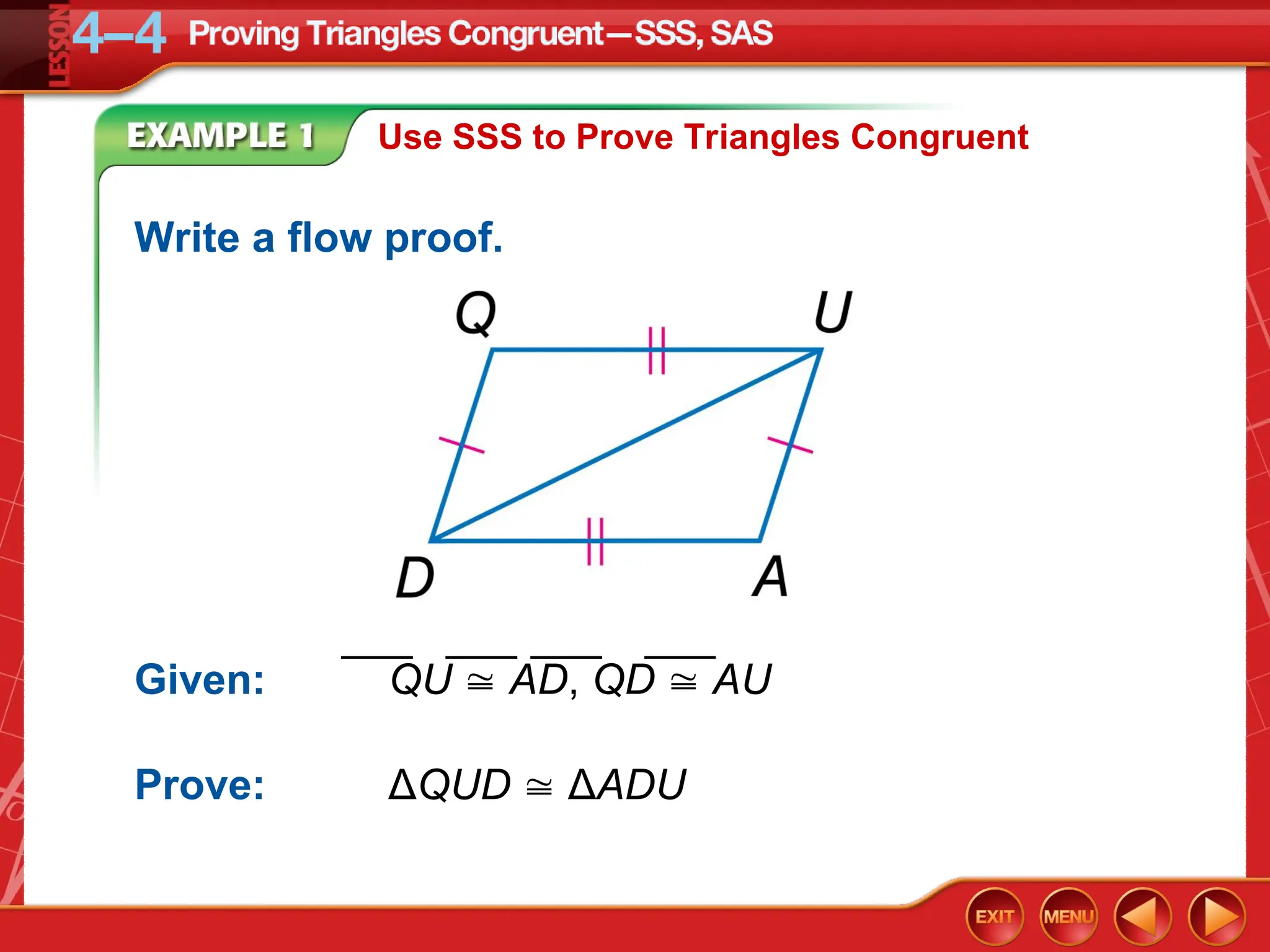
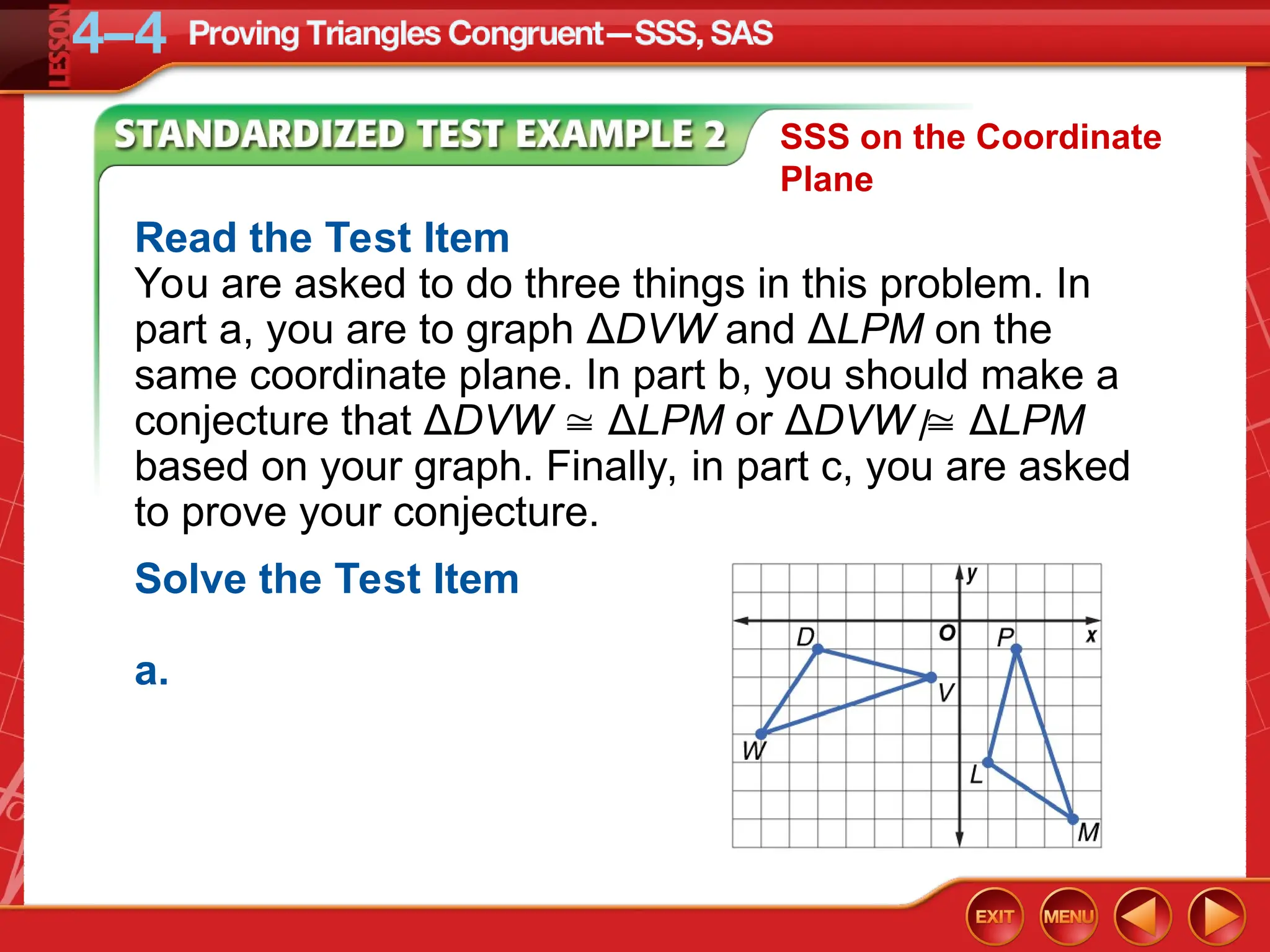
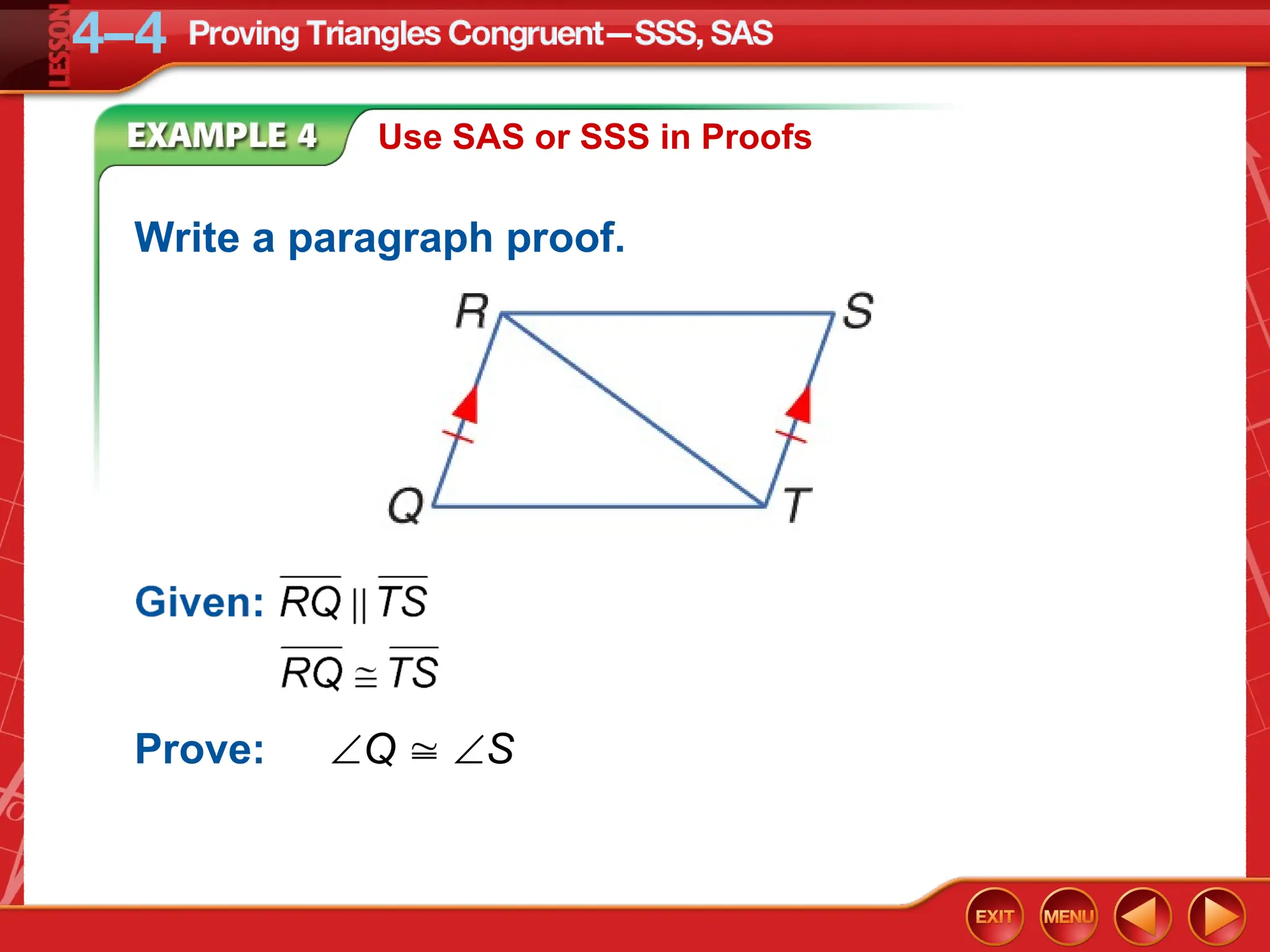
The document focuses on triangle congruence and presents various exercises related to congruence statements, corresponding angles and sides, and proofs using SSS and SAS postulates. It includes instructions to graph triangles, make conjectures, and construct logical arguments to support findings about triangle congruence. The content aligns with geometry standards and incorporates coordinate geometry approaches for solving problems related to triangle relationships.

1. SPLASH SCREEN

2. Over Lesson 4–3
A. ΔLMN  ΔRTS
B. ΔLMN  ΔSTR
C. ΔLMN  ΔRST
D. ΔLMN  ΔTRS
Write a congruence
statement for the
triangles.

3. Over Lesson 4–3
A. L  R, N  T, M  S
B. L  R, M  S, N  T
C. L  T, M  R, N  S
D. L  R, N  S, M  T
Name the corresponding
congruent angles for the
congruent triangles.

4. Over Lesson 4–3
Name the corresponding
congruent sides for the
congruent triangles.
A. LM  RT, LN  RS, NM  ST
B. LM  RT, LN  LR, LM  LS
C. LM  ST, LN  RT, NM  RS
D. LM  LN, RT  RS, MN  ST
___
___ ___ ___
___ ___
___ ___ ___ ___ ___ ___
___ ___
___ ___ ___ ___
___ ___ ___ ___ ___ ___

5. Over Lesson 4–3
A. 1
B. 2
C. 3
D. 4
Refer to the figure.
Find x.

6. Over Lesson 4–3
A. 30
B. 39
C. 59
D. 63
Refer to the figure.
Find m A.

7. Over Lesson 4–3
Given that ΔABC  ΔDEF, which of the following
statements is true?
A. A  E
B. C  D
C. AB  DE
D. BC  FD
___ ___
___ ___

8. CCSS
Content Standards
G.CO.10 Prove theorems about triangles.
G.SRT.5 Use congruence and similarity criteria for
triangles to solve problems and to prove
relationships in geometric figures.
Mathematical Practices
3 Construct viable arguments and critique the
reasoning of others.
1 Make sense of problems and persevere in solving
them.

9. THEN/NOW
You proved triangles congruent using the
definition of congruence.
• Use the SSS Postulate to test for triangle
congruence.
• Use the SAS Postulate to test for triangle
congruence.

10. VOCABULARY
• included angle

11. CONCEPT 1

12. Use SSS to Prove Triangles Congruent
Write a flow proof.
Prove: ΔQUD  ΔADU
Given: QU  AD, QD  AU
___ ___ ___ ___

13. Use SSS to Prove Triangles Congruent
Answer: Flow Proof:

14. Which information is missing from the flowproof?
Given: AC  AB
D is the midpoint of BC.
Prove: ΔADC  ΔADB
___ ___
A. AC  AC
B. AB  AB
C. AD  AD
D. CB  BC
___ ___
___ ___
___ ___
___ ___

15. EXTENDED RESPONSE Triangle DVW has vertices
D(–5, –1), V(–1, –2), and W(–7, –4). Triangle LPM has
vertices L(1, –5), P(2, –1), and M(4, –7).
a. Graph both triangles on the same coordinate
plane.
b. Use your graph to make a conjecture as to
whether the triangles are congruent. Explain
your
reasoning.
c. Write a logical argument that uses coordinate
geometry to support the conjecture you made
in
part b.
SSS on the Coordinate
Plane

16. Read the Test Item
You are asked to do three things in this problem. In
part a, you are to graph ΔDVW and ΔLPM on the
same coordinate plane. In part b, you should make a
conjecture that ΔDVW  ΔLPM or ΔDVW  ΔLPM
based on your graph. Finally, in part c, you are asked
to prove your conjecture.
/
Solve the Test Item
a.
SSS on the Coordinate
Plane

17. b. From the graph, it appears that the triangles have
the same shapes, so we conjecture that they are
congruent.
c. Use the Distance Formula to show all
corresponding sides have the same measure.
SSS on the Coordinate
Plane

18. SSS on the Coordinate
Plane

19. Answer: WD = ML, DV = LP, and VW = PM. By
definition of congruent segments, all
corresponding segments are congruent.
Therefore, ΔDVW  ΔLPM by SSS.
SSS on the Coordinate
Plane

20. A. yes
B. no
C. cannot be determined
Determine whether ΔABC  ΔDEF
for A(–5, 5), B(0, 3), C(–4, 1),
D(6, –3), E(1, –1), and F(5, 1).

21. CONCEPT 2

22. Use SAS to Prove Triangles are
Congruent
ENTOMOLOGY The wings of one type of moth
form two triangles. Write a two-column proof to
prove that ΔFEG  ΔHIG if EI  FH, and G is the
midpoint of both EI and FH.

23. Use SAS to Prove Triangles are
Congruent
3. Vertical Angles
Theorem
3. FGE  HGI
2. Midpoint Theorem
2.
Prove: ΔFEG  ΔHIG
4. SAS
4. ΔFEG  ΔHIG
Given: EI  FH; G is the midpoint of both EI and FH.
1. Given
1. EI  FH; G is the midpoint of
EI; G is the midpoint of FH.
Proof:
Reasons
Statements

24. A. Reflexive B. Symmetric
C. Transitive D. Substitution
3. SSS
3. ΔABG ΔCGB
2. ? Property
2.
1.
Reasons
Proof:
Statements
1. Given
The two-column proof is shown to prove that
ΔABG  ΔCGB if ABG  CGB and AB  CG.
Choose the best reason to fill in the blank.

25. Use SAS or SSS in Proofs
Write a paragraph proof.
Prove: Q  S

26. Use SAS or SSS in Proofs
Answer:

27. Choose the correct reason to complete the
following flow proof.
A. Segment Addition Postulate
B. Symmetric Property
C. Midpoint Theorem
D. Substitution