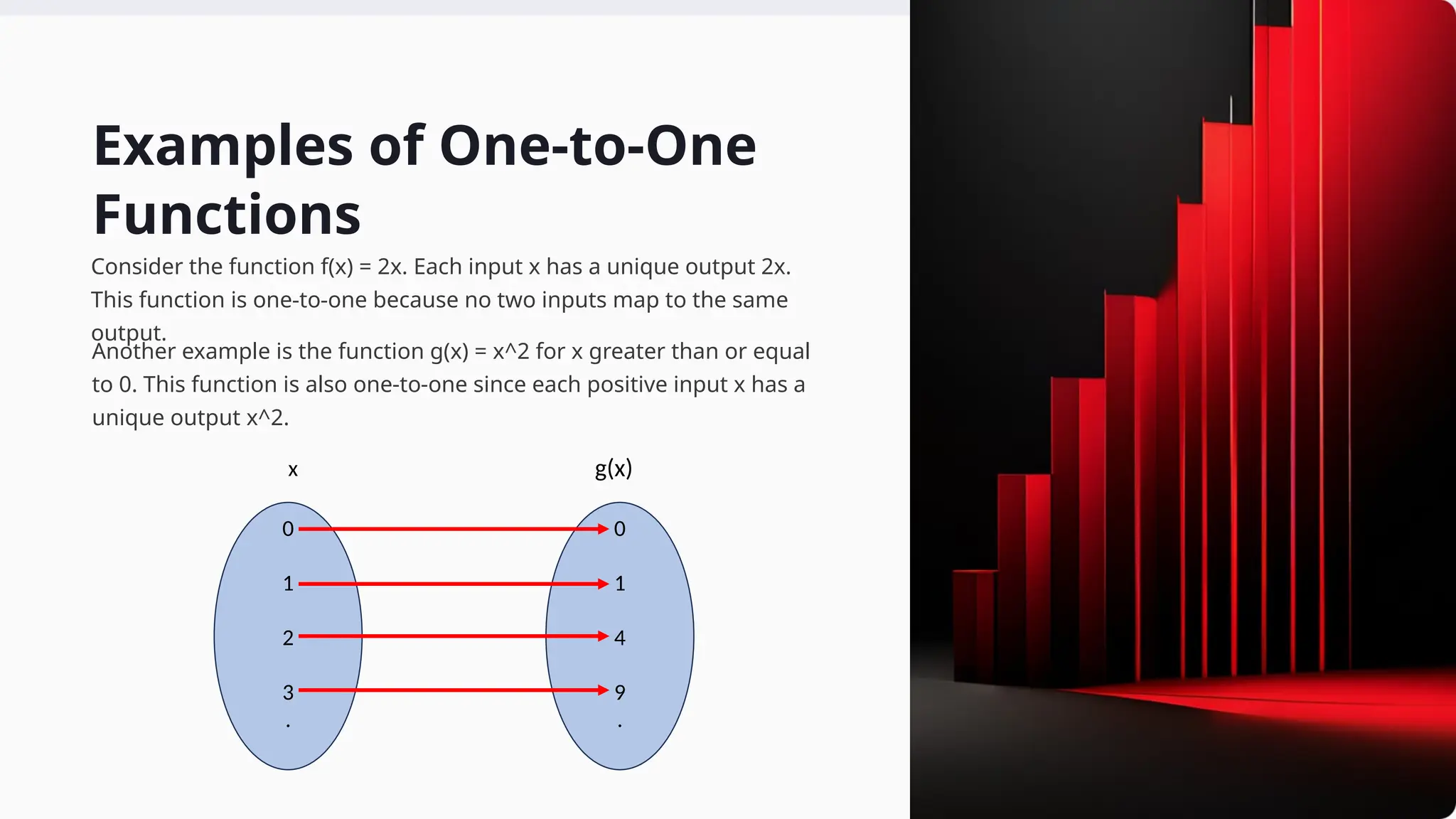
The document discusses the definition and properties of functions, focusing on one-to-one (injective) and onto (surjective) functions, along with their characteristics and examples. It introduces the pigeonhole principle, explaining its mathematical significance and various real-world applications, including scheduling and computer science. The document highlights the importance of these concepts in understanding relationships in mathematics.

1. Functions:
Definition and
Properties
Functions are essential mathematical objects that describe
relationships between sets. They are a core concept in many areas of
mathematics, such as calculus, linear algebra, and analysis.

2. One-to-One Functions (Injective
Functions)
In mathematics, a one-to-one function, also known as an injective function, is a function that maps
distinct elements of its domain to distinct elements of its codomain. This means that no two
distinct elements in the domain are mapped to the same element in the codomain.
Definition
Each element of the domain maps to a unique element of
the codomain.
2
Horizontal Line Test
A horizontal line intersects the graph of a one-to-
one function at most once.
3
Injectivity
For all x1 and x2 in the domain, if f(x1) =
f(x2), then x1 = x2.

3. A function f: A ->B is said to be a one-to-one function from A to B if different
elements of A have different images in B under f. i.e if f(a1)=f(a2) then a1=a2
where a1,a2 A.
∈
One-to-One Functions (Injective
Functions)

4. Examples of One-to-One
Functions
Consider the function f(x) = 2x. Each input x has a unique output 2x.
This function is one-to-one because no two inputs map to the same
output.
Another example is the function g(x) = x^2 for x greater than or equal
to 0. This function is also one-to-one since each positive input x has a
unique output x^2.
0
1
2
3
.
0
1
4
9
.
x g(x)

5. Properties of Functions

6. PROBLEMS:
1) Let A={1,2,3,4} . Determine whether or not the following relations on A are functions:
a) f={(2,3), (1,4), (2,1), (3,2), (4,4)}
b) g={(2,1), (3,4), (1,4), (2,1), (4,4)}
Solu:
a) We see that (2,3) f and (2,1) f
∈ ∈ i.e the element 2 is related to two different elements 3 and 1 under f.
∴ f is not a function.
b) We see that under g , every element of A is related to a unique element of A.
∴ g is a function from A to A.
Range of g = g(A) = {1,4}
(2,1) appears twice which has no special significance.
1
2
3
4
A f(A)
1
2
3
4
1
2
3
4
1
2
3
4

7. PROBLEMS:

8. PROBLEMS:

9. Onto Functions (Surjective Functions)
Definition
An onto function ensures that every element in the codomain has at least one
corresponding element in the domain.
Mapping
In an onto function, every element in the codomain is "mapped to" by at least one
element in the domain.
Visualization
Imagine a mapping where all elements in the codomain are "covered" by arrows from
the domain.

10. Onto Functions (Surjective Functions)

11. Examples of Onto Functions
Consider the function f(x) = x2 from the set of
real numbers to the set of non-negative real
numbers. This function is onto because every
non-negative real number has a square root,
which is its preimage under f.
For instance, the preimage of 9 is 3 (because
3^2 = 9). This means that every element in the
codomain has at least one corresponding
element in the domain.

12. PROBLEMS:

13. PROBLEMS:

14. The Pigeon Hole Principle
Simple Concept
It states that if you have
more items than containers,
at least one container must
have more than one item.
Mathematical Proof
It's a fundamental principle
used in various areas of
mathematics, including
combinatorics and set theory.
Real-World Applications
The principle has practical
applications in fields like
computer science,
cryptography, and even daily
life.

15. The Pigeon Hole Principle
p =[(m-1)
n
[

16. PROBLEMS:

17. PROBLEMS:

18. PROBLEMS:

19. Applications of the Pigeon Hole Principle
Scheduling
The pigeonhole principle can be applied to
scheduling problems. For instance, if you
have more appointments than available
time slots, at least one time slot must have
multiple appointments.
Computer Science
In computer science, the principle is used
to analyze algorithms and data structures.
It can help prove the existence of certain
properties or limitations.
Probability
The pigeonhole principle can be used to
calculate probabilities in certain situations.
For example, if you have a set of items, you
can use it to determine the probability of
picking a specific item.
Everyday Life
It applies to various everyday scenarios,
such as finding duplicates in a set of
objects or proving that two people must
share the same birthday in a group of 367
people.

20. Conclusion and
Key Takeaways
We have explored different types of functions, including one-to-one
and onto functions.
We learned about the Pigeonhole Principle and its applications in
solving real-world problems.