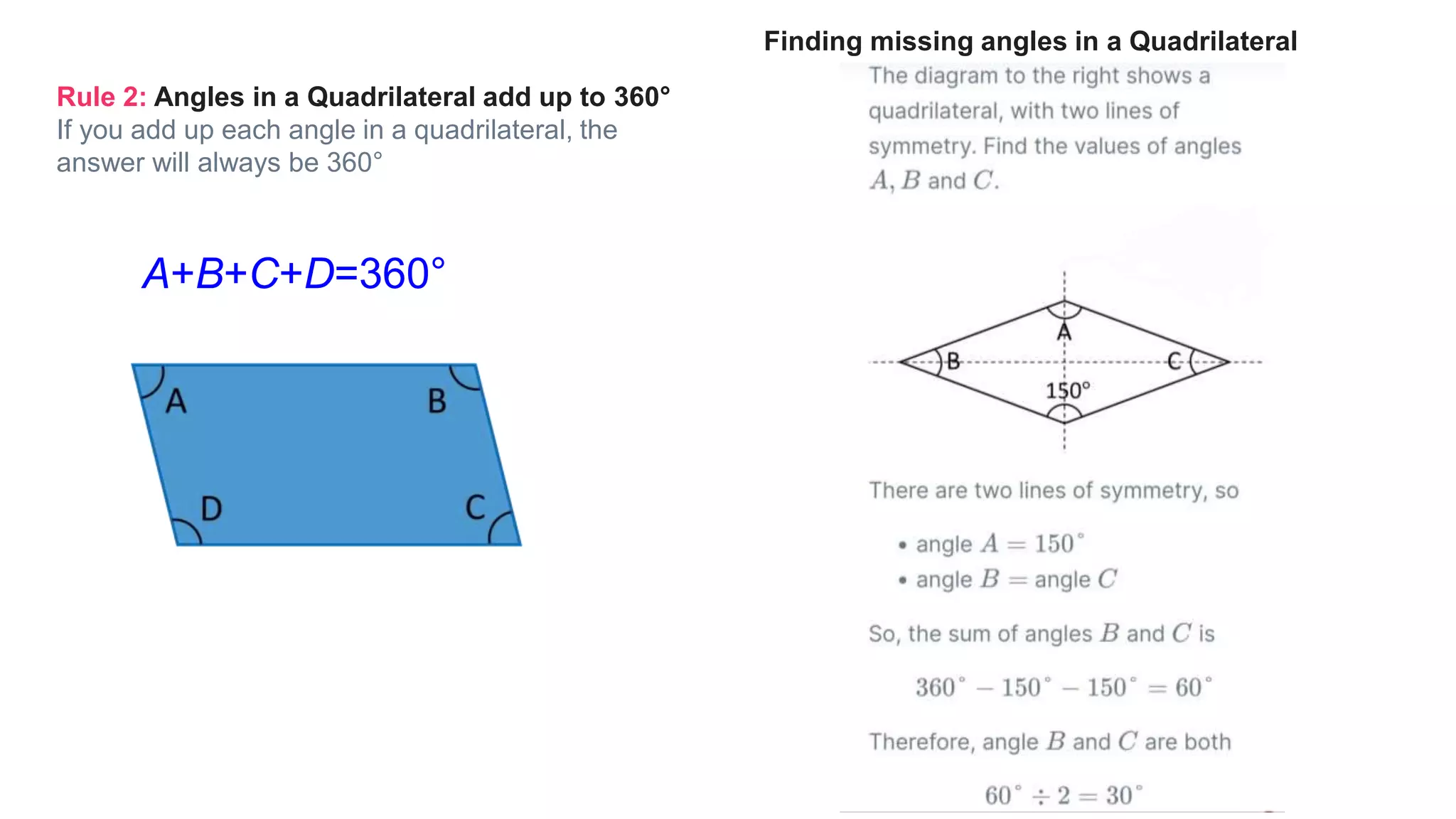
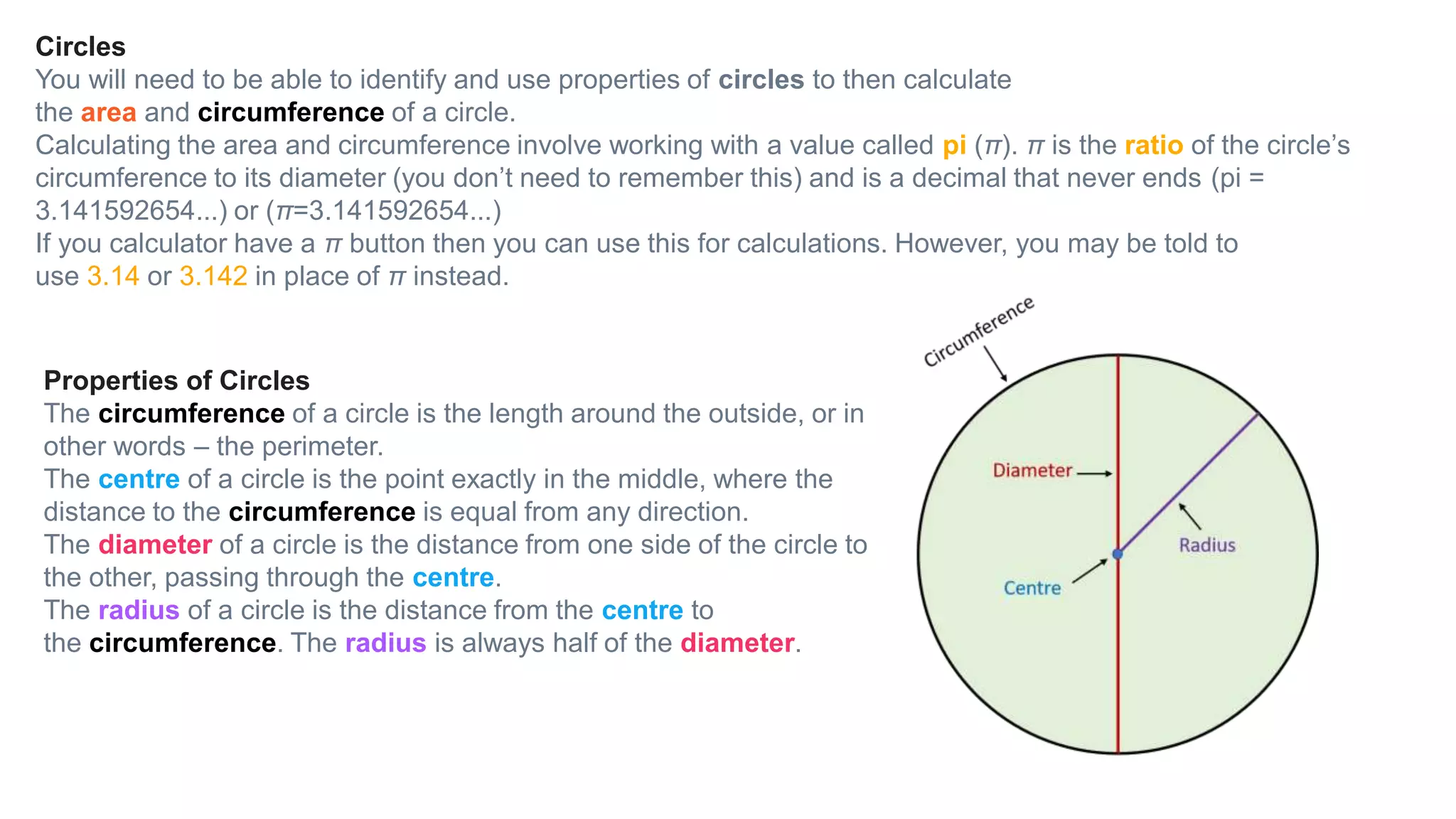
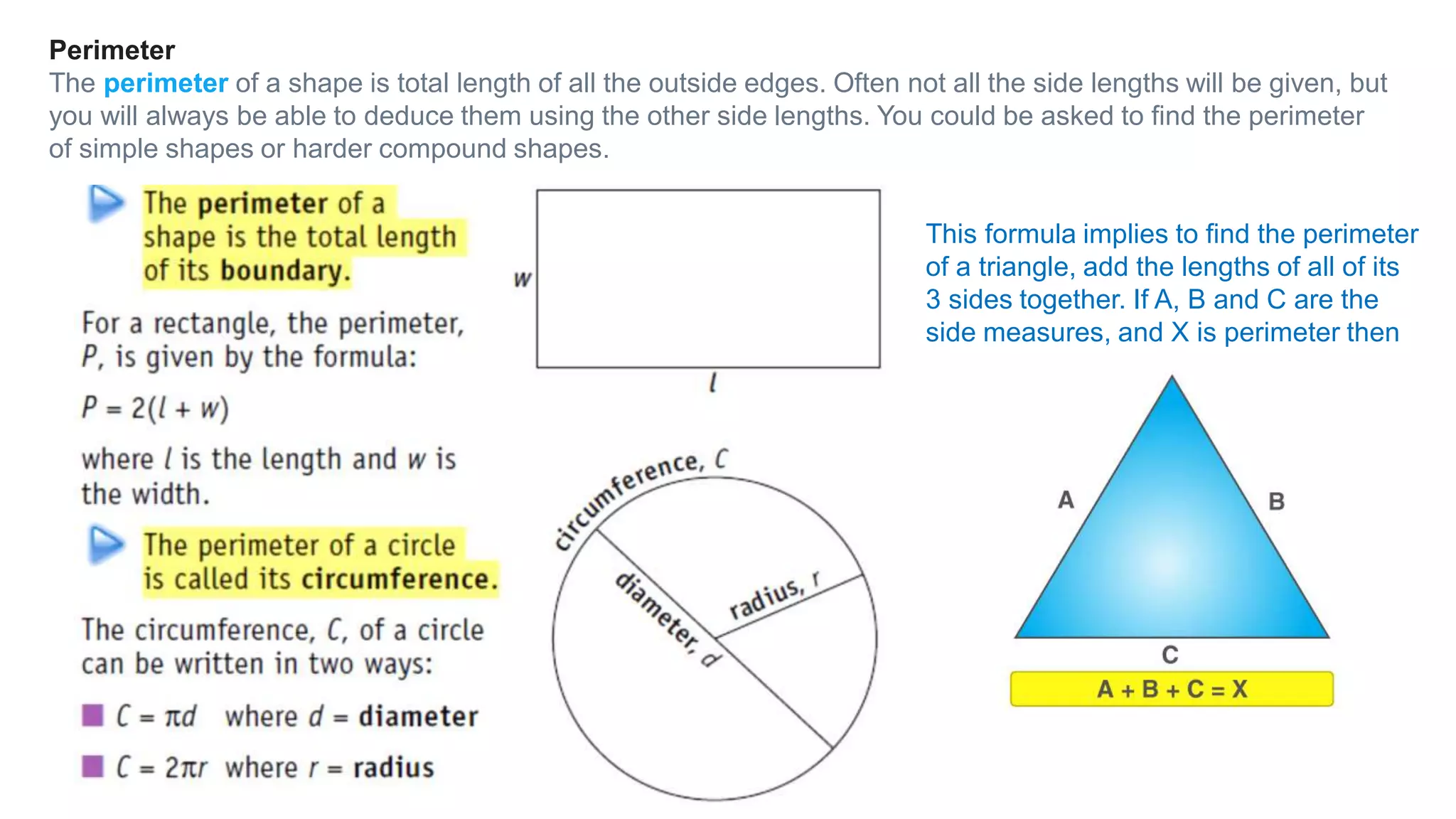
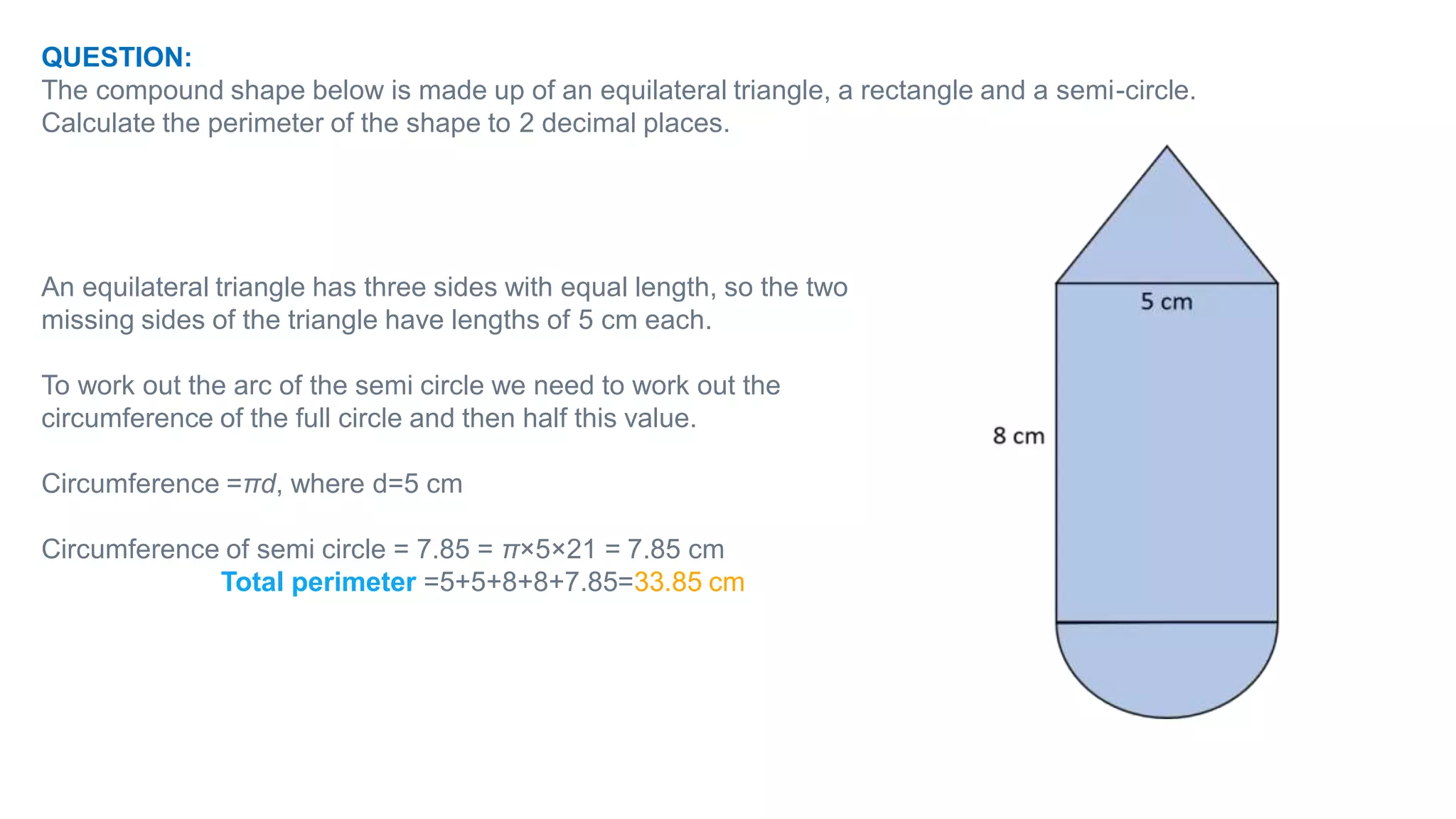
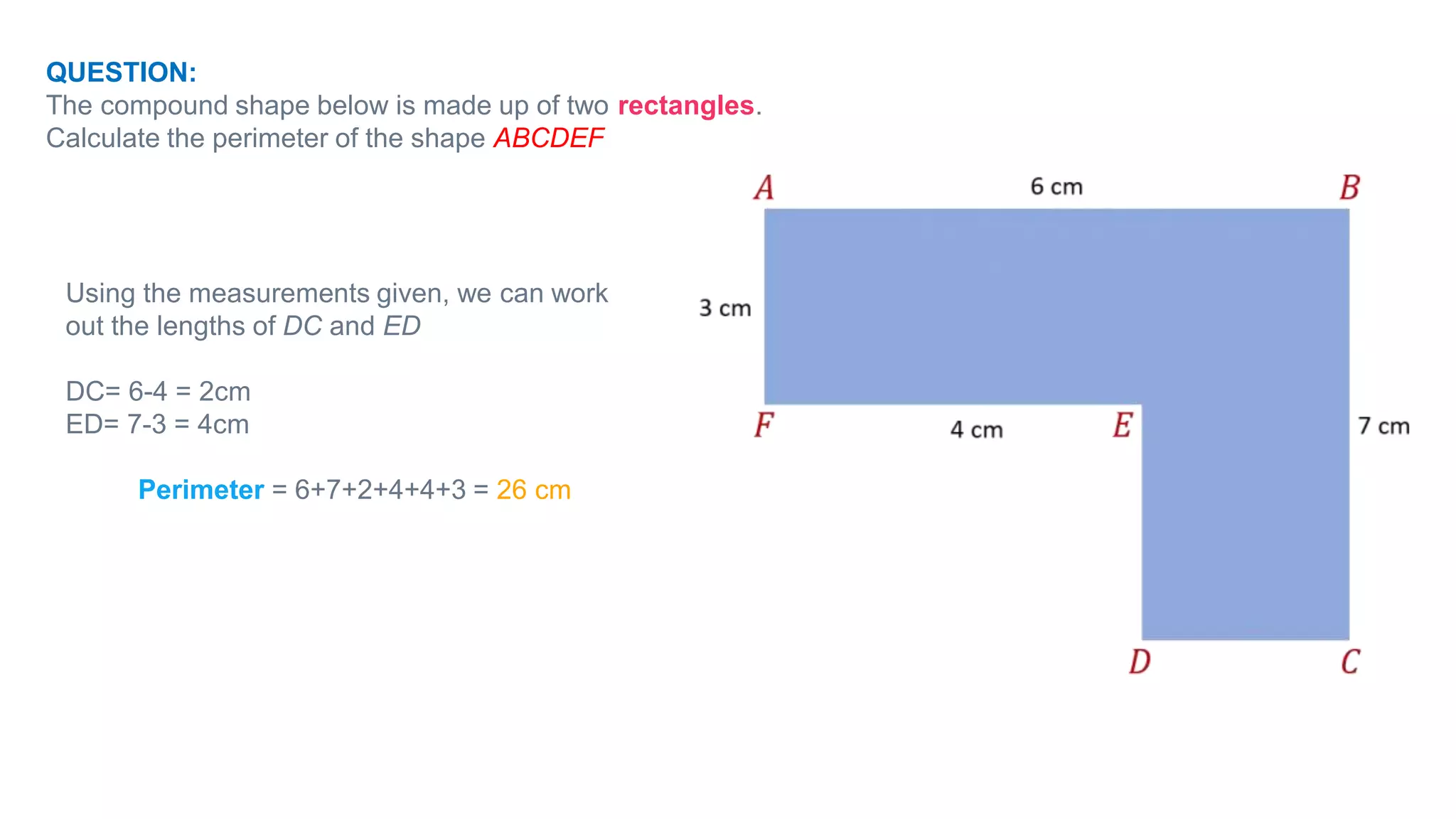
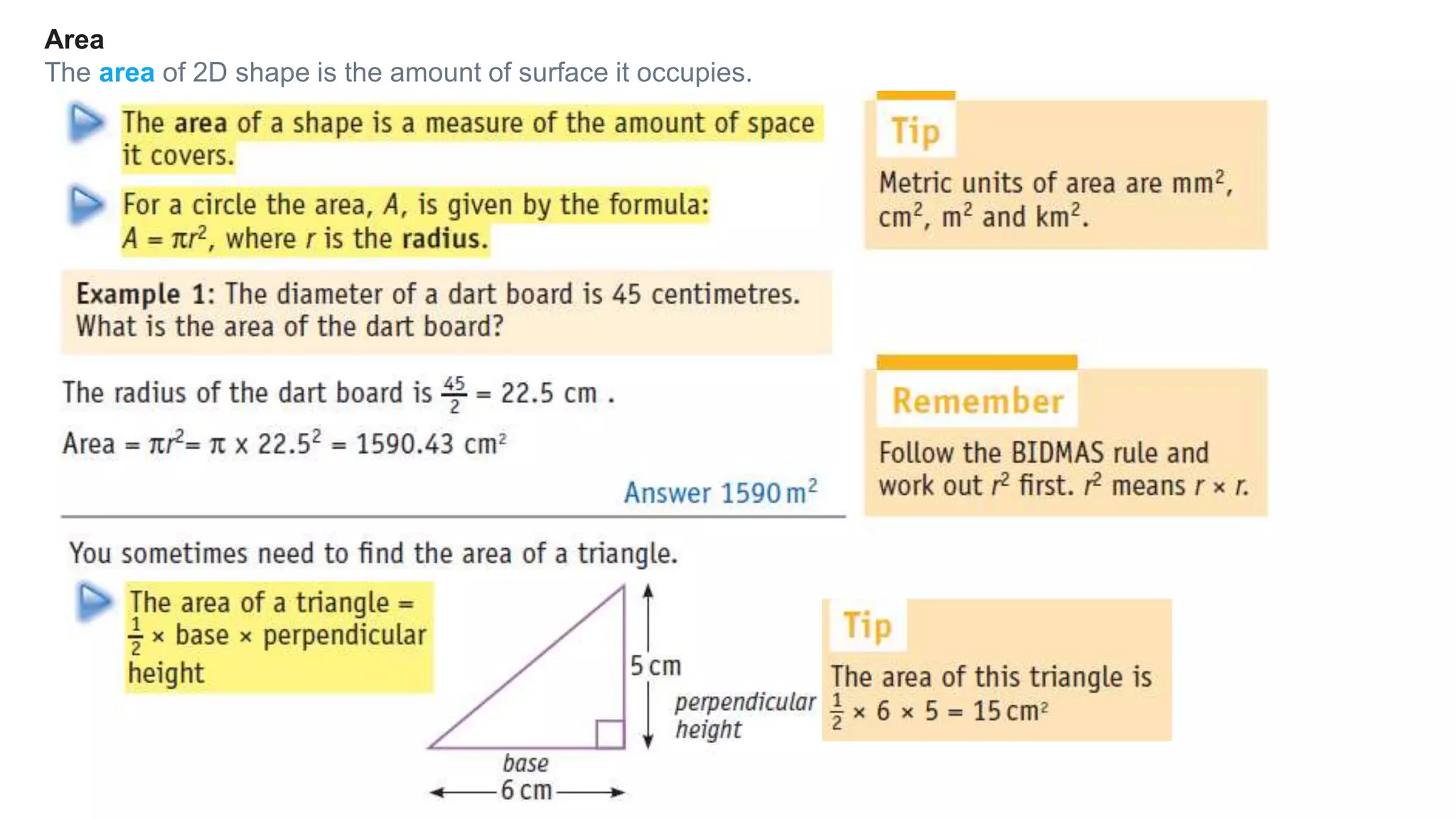
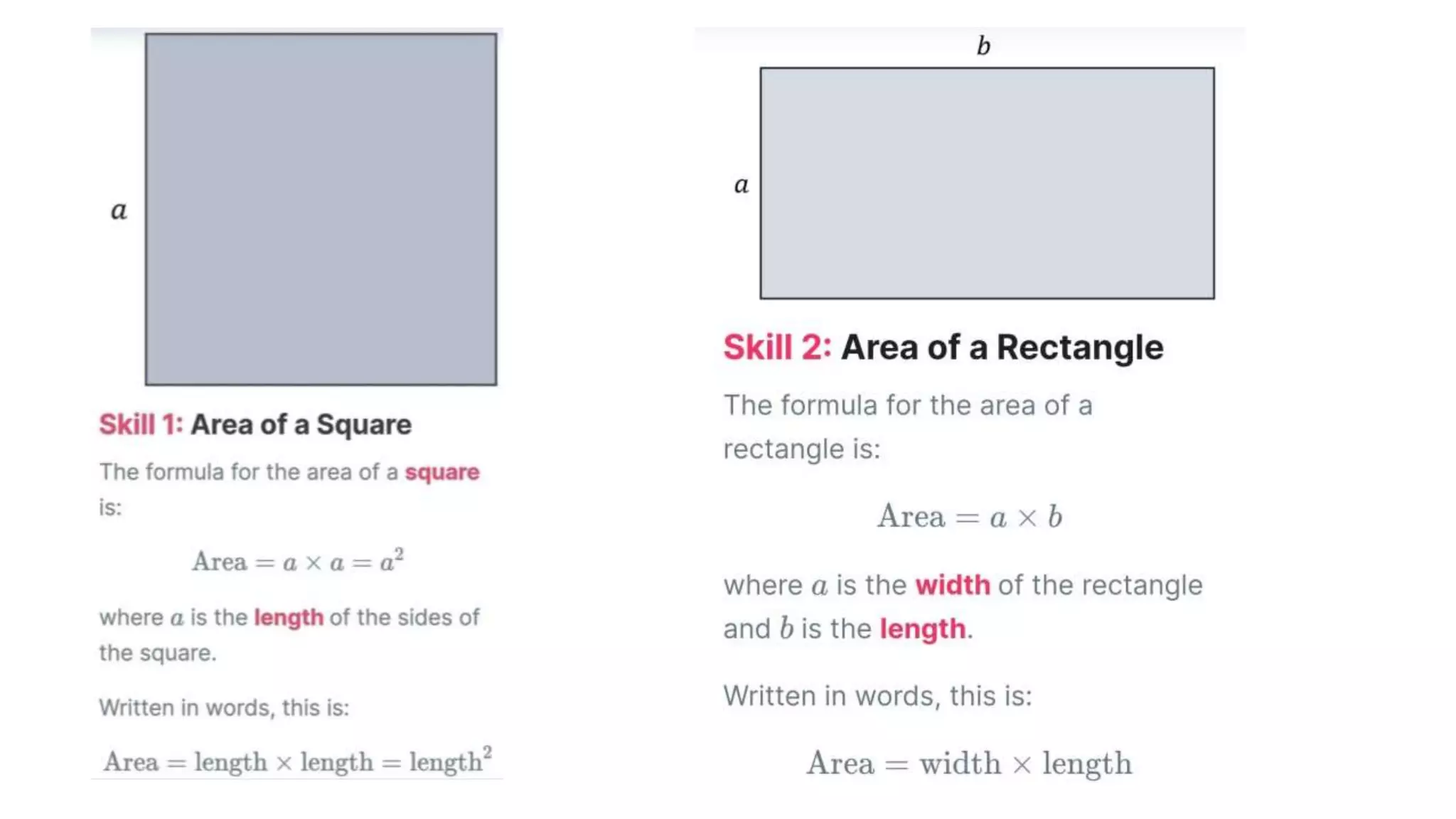
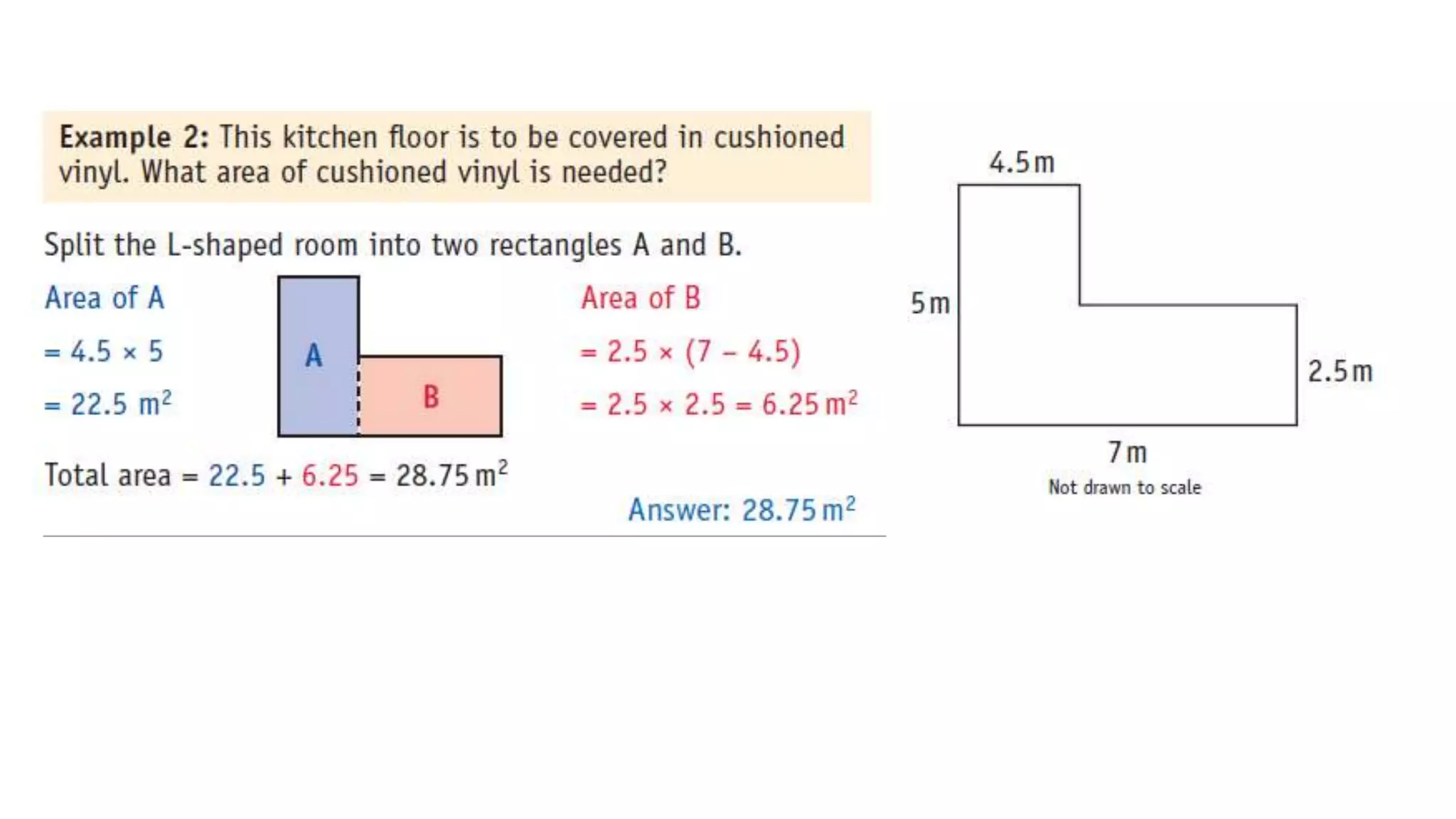
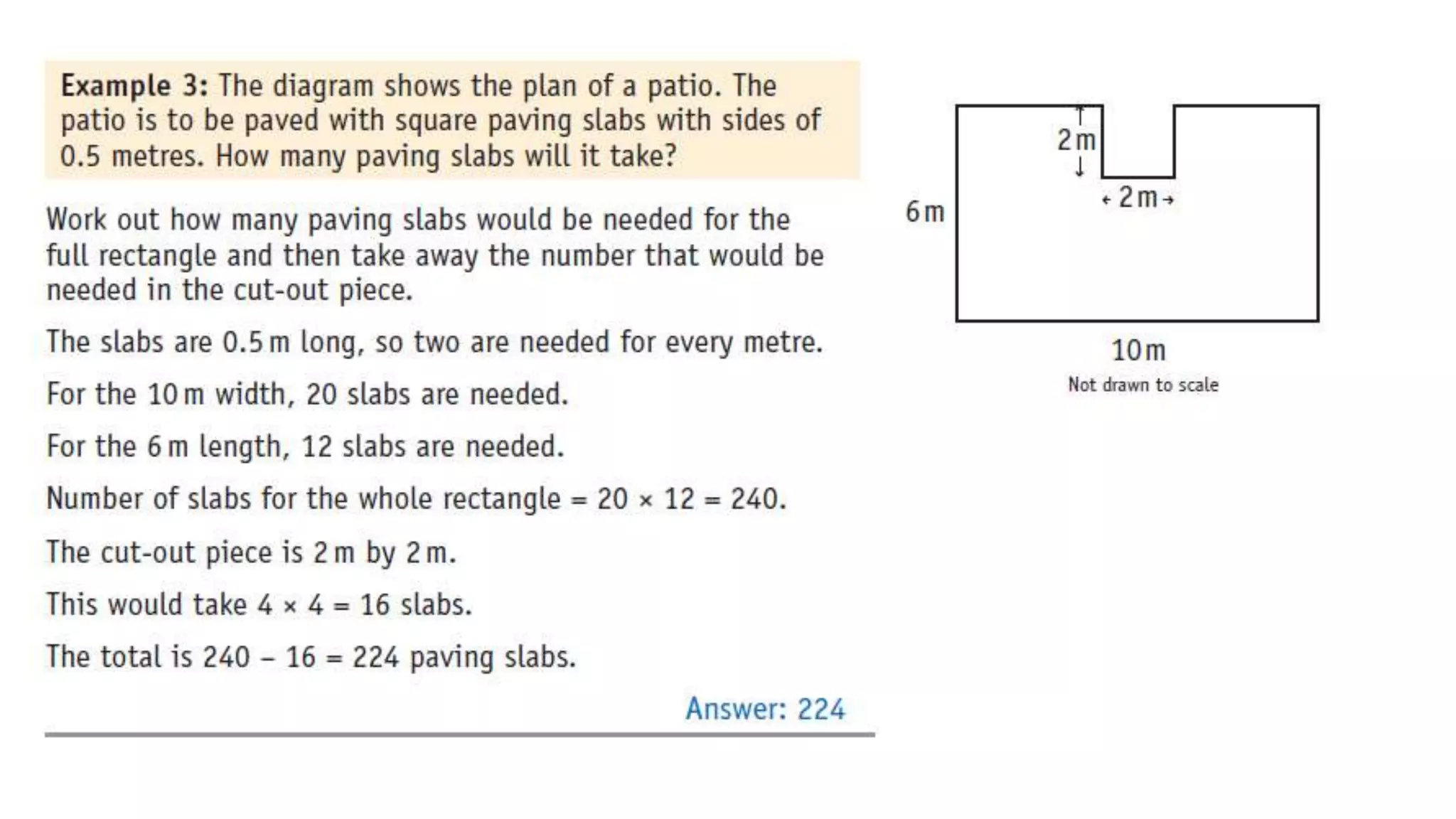
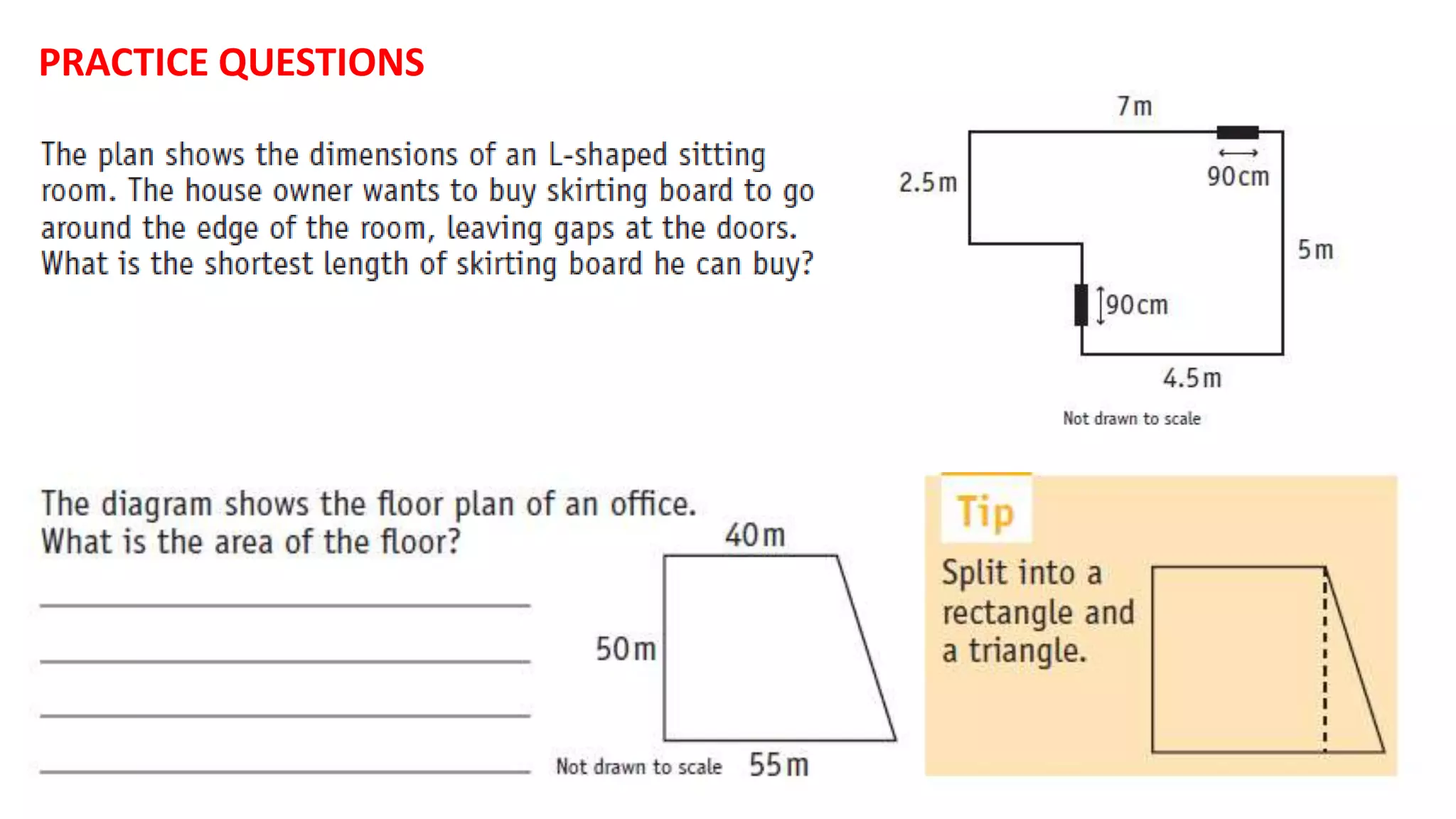
Topics covered in today's class include BIDMAS order of operations, 2D shapes, angles in 2D shapes, circles, and calculating area and perimeter. BIDMAS establishes the order for performing mathematical operations. 2D shapes were discussed along with properties of angles in triangles and quadrilaterals. Key circle properties like circumference, diameter, radius were defined. Calculating area involves using pi while perimeter finds the total length of edges. Practice questions provided calculations for perimeter of compound shapes and areas of rectangles.

1. Topics for today’s class:
BIDMAS
2D shapes
Angles in 2D shapes
Circles
Area
Perimeter

2. BIDMAS
BIDMAS (sometimes known as BODMAS) helps us remember the order in which we perform mathematical
operations. The letters stand for:
•Brackets
•Indices (or Orders)
•Division
•Multiplication
•Addition
•Subtraction
BIDMAS Calculations
Example: Calculate 5 x (2^2 + 4) – 7
Step 1: The first letter of BIDMAS is B, so look inside the brackets first. (If there are no brackets, look at indices,
and then division etc.)
In the brackets there are two operations: an index/power and an addition. The letter I comes before the
letter A in BIDMAS so first work out the result of 2^2 and then add it to 4.
(2^2 + 4) = (4 + 4) = 8
Step 2: There is a multiplication and a subtraction left, so because M comes before S, do the multiplication first
and then the subtraction,
5 x 8 - 7 = 40 - 7 = 33
So,
5 x (2^2 + 4) - 7 = 33

3. Question 1: Calculate 15×(12÷3)^2
Question 2: Calculate (2×3^3) ÷ (17−11)
Question 3: Calculate 3^2−2×3 / 24÷2​

4. 2D shapes
Angles in 2D shapes

5. 2D shapes have sides and corners, and are completely flat. Examples of 2D shapes
are circles, triangles, squares, rectangles, pentagons, hexagons and octagons!
Triangle - 3 Sides Square - 4 Sides
Pentagon - 5 Sides
Hexagon - 6 sides
Heptagon - 7 Sides
Octagon - 8 Sides
Nonagon - 9 Sides
Decagon - 10 Sides
Circle Ellipse

6. Rule 1: Angles in a Triangle add up to 180°
If you add up each angle in a triangle, the answer will
always be 180°.
You can then use this rule to find the missing angles in
triangles.
A+B+C=180°
Finding missing angles in a Triangle

7. Rule 2: Angles in a Quadrilateral add up to 360°
If you add up each angle in a quadrilateral, the
answer will always be 360°
A+B+C+D=360°
Finding missing angles in a Quadrilateral

8. Circles
You will need to be able to identify and use properties of circles to then calculate
the area and circumference of a circle.
Calculating the area and circumference involve working with a value called pi (π). π is the ratio of the circle’s
circumference to its diameter (you don’t need to remember this) and is a decimal that never ends (pi =
3.141592654...) or (π=3.141592654...)
If you calculator have a π button then you can use this for calculations. However, you may be told to
use 3.14 or 3.142 in place of π instead.
Properties of Circles
The circumference of a circle is the length around the outside, or in
other words – the perimeter.
The centre of a circle is the point exactly in the middle, where the
distance to the circumference is equal from any direction.
The diameter of a circle is the distance from one side of the circle to
the other, passing through the centre.
The radius of a circle is the distance from the centre to
the circumference. The radius is always half of the diameter.

9. Area and Perimeter

10. Perimeter
The perimeter of a shape is total length of all the outside edges. Often not all the side lengths will be given, but
you will always be able to deduce them using the other side lengths. You could be asked to find the perimeter
of simple shapes or harder compound shapes.
This formula implies to find the perimeter
of a triangle, add the lengths of all of its
3 sides together. If A, B and C are the
side measures, and X is perimeter then

12. Example: Below is a rectangle with length of 15 cm and a width of 5.5 cm
Calculate the perimeter of the rectangle.
Opposite sides of a rectangle have the same length.
Therefore, the two missing sides are 15 cm and 5.5 cm.
We can now work out the perimeter:
Perimeter = 5.5+5.5+15+15 = 41 cm

13. QUESTION:
The compound shape below is made up of an equilateral triangle, a rectangle and a semi-circle.
Calculate the perimeter of the shape to 2 decimal places.
An equilateral triangle has three sides with equal length, so the two
missing sides of the triangle have lengths of 5 cm each.
To work out the arc of the semi circle we need to work out the
circumference of the full circle and then half this value.
Circumference =πd, where d=5 cm
Circumference of semi circle = 7.85 = π×5×21​ = 7.85 cm
Total perimeter =5+5+8+8+7.85=33.85 cm

14. QUESTION:
The compound shape below is made up of two rectangles.
Calculate the perimeter of the shape ABCDEF
Using the measurements given, we can work
out the lengths of DC and ED
DC= 6-4 = 2cm
ED= 7-3 = 4cm
Perimeter = 6+7+2+4+4+3 = 26 cm

15. Area
The area of 2D shape is the amount of surface it occupies.

19. PRACTICE QUESTIONS