This document discusses formalizing the semantics of SQL and Cypher query languages. It provides an overview of SQL, including its standardization history and ambiguities in its natural language specification. The document then proposes a formal semantics for a core fragment of SQL defined using mathematical notation. It discusses challenges in validating the semantics and extending the approach to Cypher. The goal is to avoid ambiguities, define the languages precisely, and provide implementations with a clear specification.

1. Formal Semantics of SQL
(and Cypher)
Paolo Guagliardo

2. SQL
• Standard query language for relational databases
• $30B/year business
• Implemented in all major RDBMSs (free and commercial)
• First standardized in 1986 (ANSI) and 1987 (ISO)
• Several revision afterwards
(SQL-89, SQL-92, SQL:1999, SQL:2003, SQL:2006, SQL:2008, SQL:2011, SQL:2016)
“The nice thing about standards is that you have
so many to choose from” — Andrew S. Tanenbaum

3. How standard is SQL?
SELECT * FROM R WHERE EXISTS (
SELECT * FROM (
SELECT R.A, R.A FROM R ) S )
Both PostgreSQL and Oracle output R
SELECT * FROM ( SELECT R.A, R.A FROM R ) S
PostgreSQL outputs a table with two columns named “A”
Oracle throws an ERROR: reference to column “A” is ambiguous

4. Who is right?
Let’s have a look at the standard!
A. If the <select list> * is simply contained in a <subquery> that is
immediately contained in an <exists predicate>, then the <select list>
is equivalent to a <value expression> that is an arbitrary <literal>.
B. Otherwise, the <select list> * is equivalent to a <value expression>
sequence in which each <value expression> is a column reference
that references a column of T and each column of T is referenced
exactly once. The columns are referenced in the ascending sequence
of their ordinal position within T.

5. … which means
SELECT * FROM R
WHERE EXISTS (
SELECT *
FROM ( SELECT R.A, R.A
FROM R ) S
)
SELECT *
FROM ( SELECT R.A, R.A
FROM R ) S
SELECT S.A, S.A
FROM ( SELECT R.A, R.A
FROM R ) S
SELECT R.A FROM R
WHERE EXISTS (
SELECT 1
FROM ( SELECT R.A, R.A
FROM R ) S
)
≡
≡

6. The Need for a Formal Semantics
• Avoid ambiguity of natural language
• Clearly defined and not subject to interpretation
• Easy to understand and implement
Previous attempts
• Many simplifying assumptions: no bags, no nulls
• No justification of correctness

7. SELECT R.A FROM R
WHERE R.A NOT IN (
SELECT S.A FROM S)
SELECT R.A FROM R
EXCEPT
SELECT S.A FROM S
SELECT R.A FROM R
WHERE NOT EXISTS (
SELECT S.A FROM S
WHERE S.A=R.A )
A
1
NULL
A
NULLR S
A
1
A
1
NULL
A
Answer

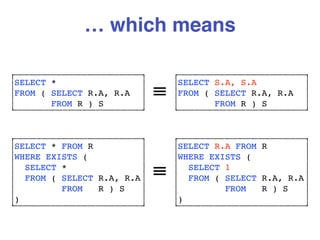
8. Core SQL fragment
⌧ := (T1, . . . , Tk), := (N1, . . . , Nk), k > 0
↵ := (A1, . . . , Am), 0
:= (N0
1, . . . , N0
m), m > 0
Queries:
Q := SELECT [DISTINCT] (↵: 0
| *) FROM ⌧ : WHERE ✓
| Q (UNION | INTERSECT | EXCEPT) [ ALL ] Q
Conditions:
✓ := TRUE | ¯t (= | 6=) ¯t | t IS [ NOT ] NULL
| ¯t [ NOT ] IN Q | EXISTS Q
| ✓ AND ✓ | ✓ OR ✓ | NOT ✓
Figure 1: Syntax of core SQL
tribute), or a pair of names (e.g., R1.A), and values are
either constants in C or NULL.
The field name fi and the field value vi of the i-th
as the only com
arbitrary compa
clause is compu
can simply atta
2.2 Semant
The semantic
database D and
a partial map fr
⌘ provides the
name and attri
fined. One star
the semantics o
vironment gets
the notation JQ
to D and ⌘; th
JQKD,?.
To explain th
definitions rela
tions on relatio
Essentially SQL without arithmetic, grouping and aggregation

9. Formal Semantics: Challenges
Data model
• Base relations / query outputs / intermediate results
• Primitive data manipulation operations
Attribute references
• Binding rules in subqueries
• Environment collects and propagates bindings

10. Proposed Semantics
JRKD,⌘ = RD
J⌧ : KD,⌘ = J(T1, . . . , Tk) : (N1, . . . , Nk)KD,⌘ = N1.JT1KD,⌘ ⇥ · · · ⇥ Nk.JTkKD,⌘
s
FROM ⌧ :
WHERE ✓
{
D,⌘
= ¯a 2 J⌧ : KD,⌘ | J✓KD,⌘;⌘¯a = t
t
SELECT ⇤
FROM ⌧ :
WHERE ✓
|
D,⌘
=
s
FROM ⌧ :
WHERE ✓
{
D,⌘
: 1
t
SELECT ↵ : 0
FROM ⌧ :
WHERE ✓
|
D,⌘
= ⇡↵
s
FROM ⌧ :
WHERE ✓
{
D,⌘
!
: 0
t
SELECT DISTINCT ↵ : 0
| ⇤
FROM ⌧ :
WHERE ✓
|
D,⌘
= "
0
@
t
SELECT ↵ : 0
| ⇤
FROM ⌧ :
WHERE ✓
|
D,⌘
1
A
JTRUEKD,⌘ = t
JtKD,⌘ =
⇢
⌘(A) if t = A
t if t 2 C or t = NULL
Jt1 = t2KD,⌘ =
8
<
:
t if Jt1KD,⌘ = Jt2KD,⌘ and Jt1KD,⌘ 6= NULL and Jt2KD,⌘ 6= NULL
f if Jt1KD,⌘ 6= Jt2KD,⌘ and Jt1KD,⌘ 6= NULL and Jt2KD,⌘ 6= NULL
u if Jt1KD,⌘ = NULL or Jt2KD,⌘ = NULL
Jt IS NULLKD,⌘ =
⇢
t if JtKD,⌘ = NULL
f if JtKD,⌘ 6= NULL
Jt IS NOT NULLKD,⌘ = ¬Jt IS NULLKD,⌘
J(t1, . . . tn) = (t0
1, . . . , t0
n)KD,⌘ =
n^
i=1
Jti = t0
iKD,⌘ J(t1, . . . tn) 6= (t0
1, . . . , t0
n)KD,⌘ =
n_
i=1
Jti 6= t0
iKD,⌘
J¯t IN QKD,⌘ =
8
<
:
t if 9¯r 2 JQKD,⌘ : J¯t = ⌫(¯r)KD,⌘ = t
f if 8¯r 2 JQKD,⌘ : J¯t = ⌫(¯r)KD,⌘ = f
u if @¯r 2 JQKD,⌘ : J¯t = ⌫(¯r)KD,⌘ = t and 9¯r 2 JQKD,⌘ : J¯t = ⌫(¯r)KD,⌘ 6= f
J¯t NOT IN QKD,⌘ = ¬J¯t IN QKD,⌘
JEXISTS QKD,⌘ =
⇢
t if JQKD,⌘ 6= ?
f if JQKD,⌘ = ?
J✓1 AND ✓2KD,⌘ = J✓1KD,⌘ ^ J✓2KD,⌘ J✓1 OR ✓2KD,⌘ = J✓1KD,⌘ _ J✓2KD,⌘ JNOT ✓KD,⌘ = ¬J✓KD,⌘
JQ1 UNION ALL Q2KD,⌘ = JQ1KD,⌘ [ JQ2KD,⌘ : `(JQ1K)
JQ1 INTERSECT ALL Q2KD,⌘ = JQ1KD,⌘ JQ2KD,⌘ : `(JQ1K)
JQ1 EXCEPT ALL Q2KD,⌘ = JQ1KD,⌘ JQ2KD,⌘ : `(JQ1K)
JQ1 ? Q2KD,⌘ = " JQ1 ? ALL Q2KD,⌘ , ? 2 {UNION, INTERSECT}
JQ1 EXCEPT Q2KD,⌘ = "(JQ1KD,⌘) JQ2KD,⌘ : `(JQ1K)
Figure 2: Semantics of core SQL
• Fits in one page
• Non-ambiguous
• Easy to understand
• Easy to implement
• Easy to modify

11. Formal Semantics: Validation
• Cannot prove that semantics is correct
• Provide sufficient experimental evidence
• Implemented in Python
• Validated on 100000+ random SQL queries

12. Formal Semantics of Cypher
• Collaboration between Neo Technology
and the University of Edinburgh
• Preliminary meeting in December
• Legal agreements finalized recently
• Neo Technology sponsors a researcher
(Nadime Francis)

13. Challenges
• Getting the (abstract) data model right
• Intermediate representation (QUIL?)
• Identify core fragment
• Language constantly evolving
• Follow the footsteps of SQL? (nulls)