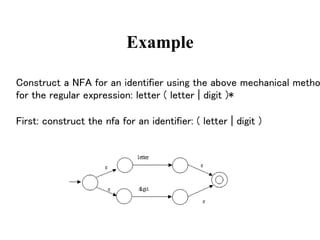
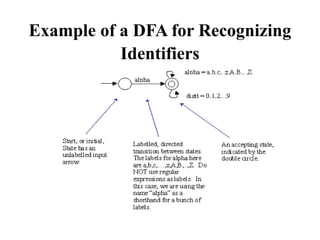
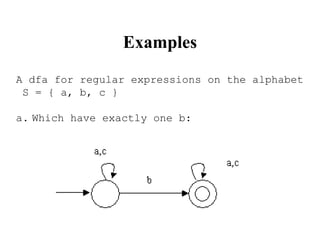
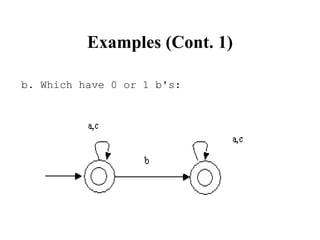
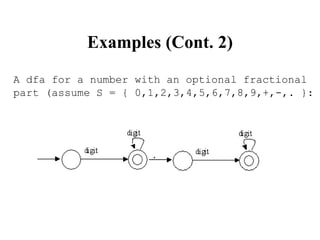
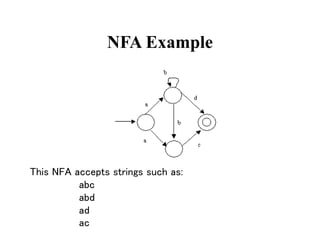
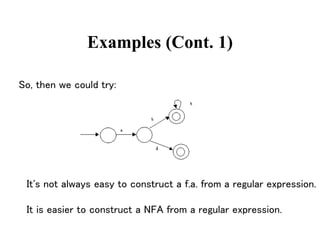
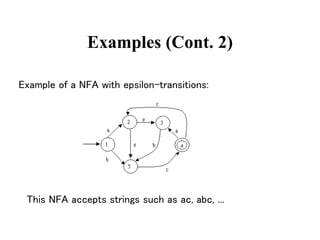
This document discusses deterministic finite automata (DFAs) and how they are used to recognize regular expressions and generate lexical analysis tables. It provides examples of DFAs for specific regular expressions. It also discusses how to construct a nondeterministic finite automaton (NFA) from a regular expression using basic building blocks. The document then gives an example of constructing an NFA for an identifier regular expression using the described mechanical method.

1. ICS312 Set 29
Deterministic Finite Automata
Nondeterministic Finite Automata

2. Deterministic Finite Automata
• A regular expression can be represented (and recognized) by a
machine called a deterministic finite automaton (dfa).
• A dfa can then be used to generate the matrix (or table) used by
the scanner (or lexical analyzer).
• Deterministic finite automata are frequently also called simply
finite automata (fa).

3. Example of a DFA for Recognizing
Identifiers

4. Examples
A dfa for regular expressions on the alphabet
S = { a, b, c }
a. Which have exactly one b:

5. Examples (Cont. 1)
b. Which have 0 or 1 b's:

6. Examples (Cont. 2)
A dfa for a number with an optional fractional
part (assume S = { 0,1,2,3,4,5,6,7,8,9,+,-,. }:

7. Constructing DFA
• Regular expressions give us rules for recognizing the
symbols or tokens of a programming language.
• The way a lexical analyzer can recognize the symbols
is to use a DFA (machine) to construct a matrix, or
table, that reports when a particular kind of symbol
has been recognized.
• In order to recognize symbols, we need to know how
to (efficiently) construct a DFA from a regular
expression.

8. How to Construct a DFA from a
Regular Expression
• Construct a nondeterministic finite automata
(nfa)
• Using the nfa, construct a dfa
• Minimize the number of states in the dfa to get
a smaller dfa

9. Nondeterministic Finite Automata
• A nondeterministic finite automata (NFA) allows
transitions on a symbol from one state to possibly
more than one other state.
• Allows e-transitions from one state to another
whereby we can move from the first state to the
second without inputting the next character.
• In a NFA, a string is matched if there is any path from
the start state to an accepting state using that string.

10. NFA Example
This NFA accepts strings such as:
abc
abd
ad
ac

11. Examples
a f.a. for ab*:
a f.a. for ad
To obtain a f.a. for: ab* | ad We could try:
but this doesn't work, as it matches strings such as abd

12. Examples (Cont. 1)
So, then we could try:
It's not always easy to construct a f.a. from a regular expression.
It is easier to construct a NFA from a regular expression.

13. Examples (Cont. 2)
Example of a NFA with epsilon-transitions:
This NFA accepts strings such as ac, abc, ...

14. Algorithm to employ in getting a
computer program to construct a
NFA for any regular expression
Basic building blocks:
(1) Any letter a of the alphabet is recognized by:
(2) The empty set  is recognized by:

15. Note: it is possible to avoid including some of the ε-productions
employed by the algorithm, but the increase in speed, if any, is
negligible.
(3) The empty string e is recognized by:
(4) Given a regular expression for R and S, assume these boxes
represent the finite automata for R and S:

16. (5) To construct a nfa for RS (concatenation):
(6) To construct a nfa for R | S (alternation):

17. (7) To construct a nfa for R* (closure):

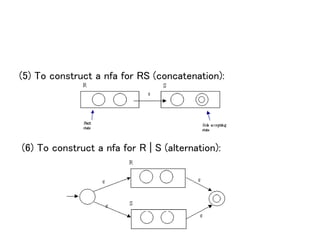
18. NOTE: In 1-3 above we supply finite automata for
some basic regular expressions, and in 4-6 we
supply 3 methods of composition to form finite
automata for more complicated regular expressions.
These, in particular, provide methods for
constructing finite automata for regular expressions
such as, e.g.:
R+ = RR*
R? = R | ε
[1-3ab] = 1|2|3|a|b

19. Example
Construct a NFA for an identifier using the above mechanical metho
for the regular expression: letter ( letter | digit )*
First: construct the nfa for an identifier: ( letter | digit )

20. Example (Cont.1)
Next, construct the closure: ( letter | digit )*
1 2
3
4
5
6
7 8
e
e
e
e
e
e
e
e
letter
digit

21. Example (Cont.2)
Now, finish the construction for: letter ( letter | digit )*