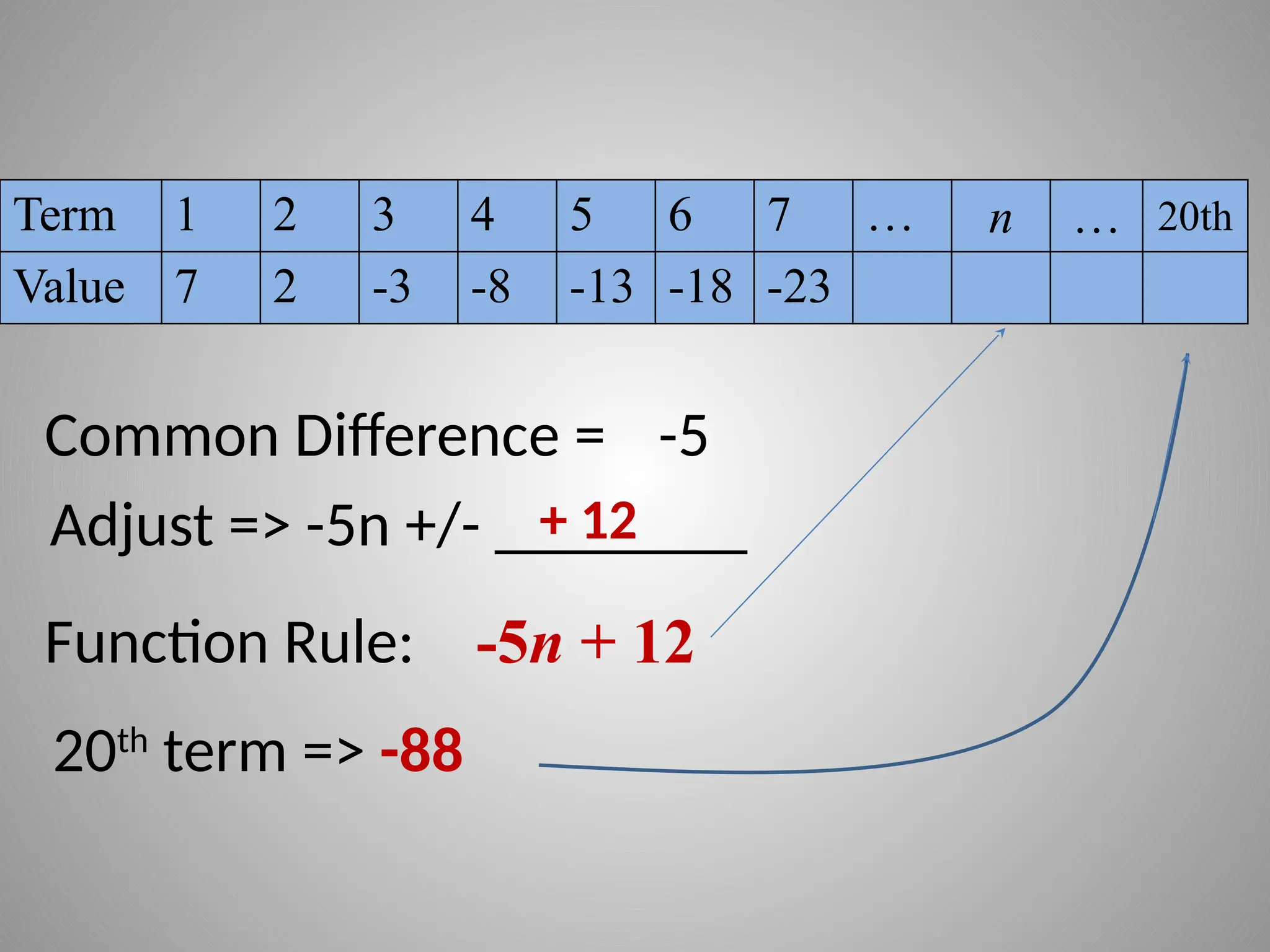
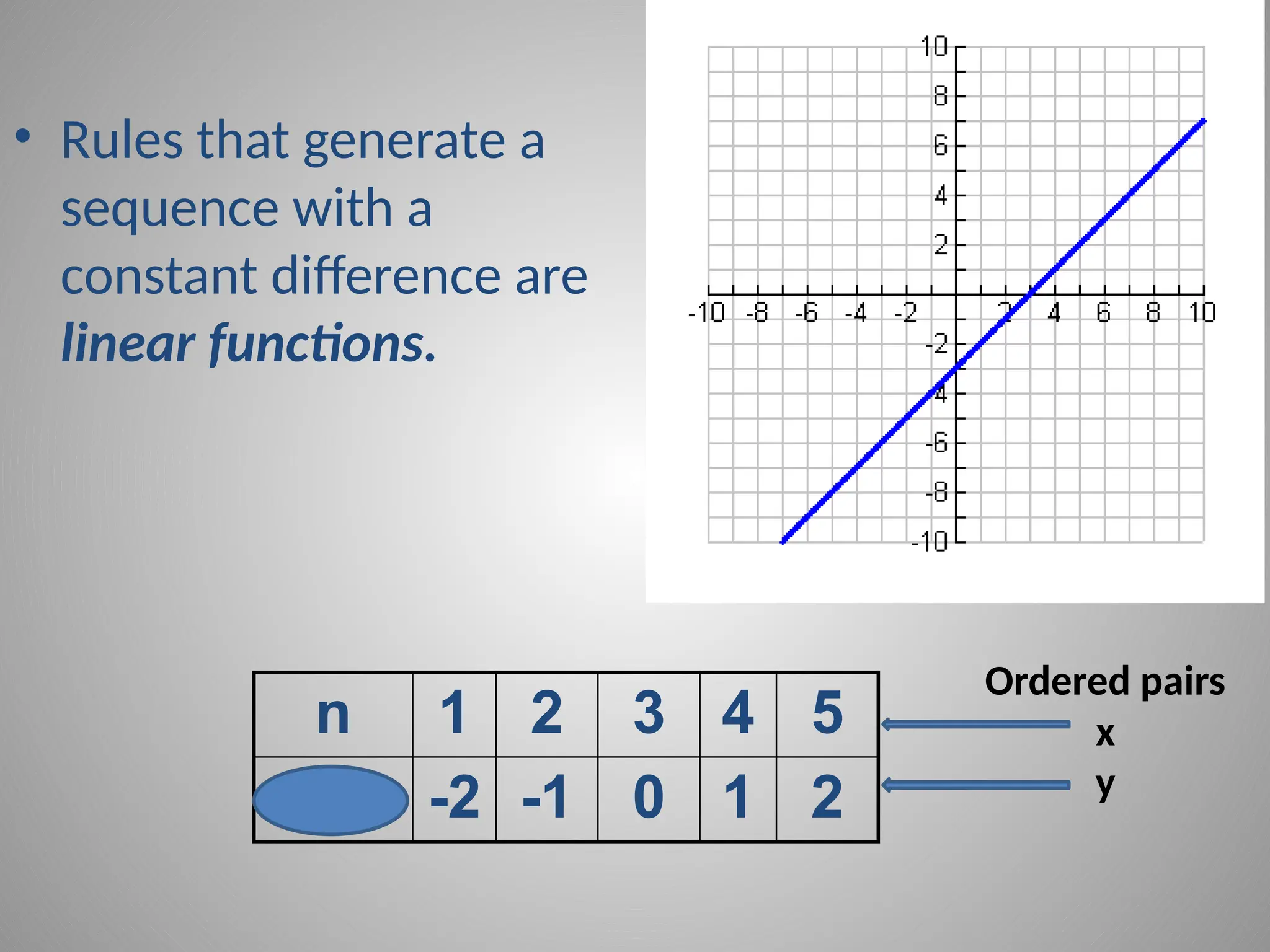
The document covers the process of finding the nth term in linear sequences through inductive reasoning and the use of function rules. It discusses the common difference in sequences and demonstrates how to create rules for predicting terms based on observed patterns. Examples of arithmetic sequences and their corresponding function rules are provided to illustrate the concepts.

1. Lesson 2.2
Finding the nth term
Writing the RULE for a Linear Sequence
Homework: lesson 2.2/1-8

2. Objectives
• Use inductive reasoning to find a pattern
• Create a rule for finding any term/value in
the sequence
• Use your rule to predict any term in the
sequence

3. Function Rule:
The rule that gives the nth term for a sequence.
n = term number (location of a value in the sequence)
20, 27, 34, 41, 48, 55, . . .
Next term?
62
200th
term?
WHY?
How do we find
this 200th
term?

7. n = 200
7n+13 => 7(200)+13
= 1413

8. Looking at 1, 4, 7, 10, 13, 16, 19, .......,
carefully helps us to make the following
observation:
As you can see, each term is found by adding 3, a
common difference from the previous term
Common Difference:

9. Looking at 70, 62, 54, 46, 38, ... carefully helps
us to make the following observation:
This time, to find each term, we subtract 8,
a common difference from the previous
term

10. • Common difference (n) +/- ‘something’
n = 1 2 3 4 5 6
values = 7, 2, -3, -8, -13, -18, …
-5 -5 -5 -5
• -5n +/-
-5(1) = -5 + 12 = 7
• nth term RULE: -5n + 12
Common
Difference
+/- something
Writing the Rule/ nth term
+ 12

11. Finding the nth Term
• Find the Common Difference
• CD becomes the coefficient of n
• add or subtract from that product to find the
sequence value +/- x
• Write the RULE
n 1 2 3 4 5 … n … 25
value 3 9 15 21 27
+6
6n
-3
6n - 3
6n-3
6(25)-3
147

12. Use the Rule to complete the pattern
n 1 2 3 4 5
n-3 -2 -1 0 1 2
n 1 2 3 4 5
2n+1 3 5 7 9 11
n 1 2 3 4 5
-4n+5 1 -3 -7 -11 -15
What pattern do
you see
consistently
emerging from all
these rules?
Are these examples
of linear or
nonlinear patterns?
Common
difference

13. Term 1 2 3 4 5 6 7 … n … 20th
Value 7 2 -3 -8 -13 -18 -23
Function Rule: -5n + 12
20th
term => -88
Common Difference = -5
Adjust => -5n +/- ________
+ 12

14. Use the pattern to find the rule & the
missing term
n 1 2 3 4 5 .. 54
6n 6 12 18 24 30 324
+6 +6 +6 +6
RULE: 6n+ _?__
Common difference = 6
n=1 6(1)+
🡪 _?__ = 6
n=2 6(2)+
🡪 ? =12
? = 0
RULE: 6n

15. n 1 2 3 4 5 .. 37
2x+5 7 9 11 13 15 79
+2 +2 +2 +2
RULE: 2n+ _?__
Common difference = 2
n=1 2(1)+
🡪 _?__ = 7
n=2 2(2)+
🡪 ? =9
? = 5
RULE: 2n+5

16. n 1 2 3 4 5 .. 50
-4n+1 -3 -7 -11 -15 -19 199
-4 -4 -4 -4
RULE: -4n+ _?__
Common difference = -4
n=1 -4(1)+
🡪 _?__ = -3
n=2 -4(2)+
🡪 ? =-7
? = +1
RULE: -4n+1

17. Use a table to find the number of squares
in the next shape in the pattern.
n n 50
# of squares
1
5
2
8
3
11 3n+2 152

18. • Rules that generate a
sequence with a
constant difference are
linear functions.
n 1 2 3 4 5
n-3 -2 -1 0 1 2
Ordered pairs
x
y

19. Rules for sequences can be expressed using
function notation.
f (n) = −5n + 12
In this case, function f takes an input value n,
multiplies it by −5, and adds 12 to produce an
output value.

20. n 1 2 3 4 5
f(n) -3 -1 3 11 27
n 1 2 3 4 5
f(n) 9 6 3 0 -3
n 1 2 3 4 5
f(n) -8 -4 0 4 8
n 1 2 3 4 5
f(n) -2 -1 1 4 8
IS THE PATTERN LINEAR?
NO YES; cd=-3
YES; cd=+4 NO

22. -5
-33
-28
-23
-18
-13
-8
-3
2
-5n + 7
+3
21
19
16
13
10
7
4
1
3n – 2
-2
-11
-9
-7
-5
-3
-1
1
3
-2n + 5
+4
29
25
21
17
13
9
5
1
4n – 3
+1
3
2
1
0
-1
-2
-3
-4
n – 5
Difference
8
7
6
5
4
3
2
1
n
Copy and complete the table
Term
Function Rule
Coefficient

24. • Find the next term in an Arithmetic and
Geometric sequence
• Arithmetic Sequence
• Formed by adding a fixed number to a previous
term
• Geometric Sequence
• Formed by multiplying by a fixed number to a
previous term

26. Arithmetic sequence formula
n represents the term you are calculating
1st
term in the sequence
d the common difference between the terms