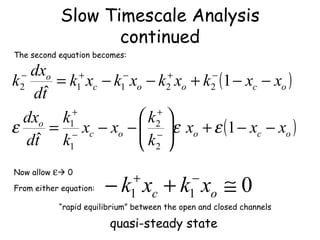
The document discusses using timescale separation to simplify dynamic models with fast and slow processes. It provides two examples: (1) a calcium ion channel model that has fast activation and slower inactivation rates, allowing separation into fast and slow timescales; (2) a reactor wall heat transfer model where the wall thermal mass is small compared to the reactor, allowing separation based on the fast temperature response of the wall and slower temperature change in the reactor. Both examples non-dimensionalize variables, identify a small parameter epsilon as the ratio of timescales, then take the fast timescale limit of epsilon to zero to obtain simplified equations representing each timescale.

1. Dynamic Modeling II Outline Timescale analysis Dynamics of calcium ion Dynamics of reactor walls Multi Compartment & Stage analysis Human skin attached to a rat.

2. Calcium Ion Channel in Cells Consider a Model of a Calcium Ion Channel in a cell membrane Channel has three States Closed Open Inactive Inactive Open Closed k + 1 K + 2 K - 2 K - 1 x i = fraction of channels in a given state i Ca 2+ Ca 2+ =Ca 2+ d Ca 2+ Low High

3. Fast & Slow Timescales If the time scale of activation is much faster than that of inactivation we can use these two different timescales to simplify the problem. k 1 >>k 2 Scale time by the slow reaction constant: Substitute into equations and look for “small parameter”  <<1 ratio of slow to fast timescales

4. Slow Timescale Analysis continued The second equation becomes: Now allow   0 From either equation: “ rapid equilibrium” between the open and closed channels quasi-steady state

5. Slow timescale continued Rapid equilibrium between open and closed, now we need a differential equation independent of  Add the two equations: Let Combined fractions of open and closed channels Have to eliminate x o from this

6. Slow Timescale Ion Channel From algebraic equation: y(0)=1 Differential Equation for y:

7. Fast Timescale Fast Timescale Differential Equations

8. Summary Analyze model parameters (reaction rate constants, heat or mass transfer coefficient) and see if there are opportunities to separate timescales into “fast” and “slow” Define/choose time constants for each scale whose ratio defines a small parameter  Non-dimensionalize the dependent variables using model parameters Non-dimensionalize the time variable at each scale and see what can be neglected by allowing   0 Analyze the simplified equations which represent the two timescales.

9. Another Example T o T R T wo T wi m w C pw m R C pR k w Heat Transfer across a reactor wall State Variables, T W and T R , note T W already lumped. Q R

10. Heat Transfer Continued Rearrange the Equations for T w and T R [time] -1 Slow time scale Transfer Rate across wall small compared to the thermal mass of reactor

11. Heat Transfer Continued The Thermal Mass of Reactor is large compared to the wall,  is ratio of wall to reactor thermal mass . The wall temperature is just the average at slow time scale.

12. Heat Transfer Continued Eliminate T W by using the relationship from the previous result Now solve the ODE

13. Fast Timescale Allow   0 Ratio of rate of heat transfer to thermal mass of the wall is large. Now solve the ODE and substitute into AE Implicitly Q R must also be slow