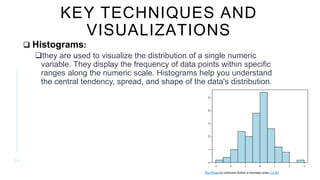
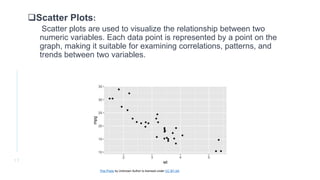
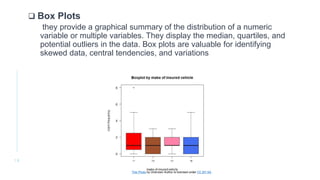
Exploratory data analysis (EDA) is an approach to analyze data using visual techniques to discover trends and patterns. EDA involves understanding the data, detecting issues, discovering patterns, and visualizing relationships. The key steps in EDA are data collection, cleaning, visualization, transformation, summarization, and feature selection. EDA plays a foundational role by assessing data quality, understanding characteristics, and testing assumptions to build accurate statistical models. Common EDA techniques include histograms, scatter plots, box plots, and heatmaps to visualize univariate and bivariate relationships in the data.

1. EXPLORATORY DATA ANALYSIS
IN STATISTICAL MODELING
SUJOY PT

2. AGENDA
2
INTRODUCTION TO EDA
THE EDA PROCESS
WHY EDA MATTERS IN STATISTICAL
MODELING
KEY TECHNIQUES AND VISUALIZATIONS
REAL-LIFE EXAMPLE
CONCLUSION

3. INTRODUCTION TO
EDA
3
Definition of EDA:
•Exploratory Data Analysis (EDA) is an approach to analyze
data using visual techniques.
•Are used to discover trends and patterns with the help of
statistical summary and graphical representation.

4. OBJECTIVES OF
EDA:
• Understand the Data
• provides insights into the dataset's content,
structure,
and characteristics.
• Detect Data Issues
• ensures that the data is clean and reliable for
analysis.
• Discover Patterns
• EDA uncovers patterns, trends, and relationships within
the data, making it easier to spot important insights.
• Detect Outliers
4

5. • Verify Model Assumptions
• checks if the assumptions needed for statistical
modeling are met, ensures that models are suitable
for the data.
• Visualize Data
• It creates charts and graphs to present data visually
and makes it easier to understand and
communicate.
5

6. THE EDA PROCESS
DATA COLLECTION:
This step involves gathering the data you want to analyze. Data can come
from various sources, such as databases, spreadsheets, or online sources.
DATA CLEANING:
Cleaning involves identifying and addressing issues like missing values,
duplicates, outliers, or inconsistencies to ensure data quality.
DATA VISUALIZATION:
Creating visual representations of the data, such as charts and graphs, to
help you understand patterns, trends, and distributions

7. DATA TRANSFORMATION:
Sometimes, data needs to be transformed to meet analysis
requirements. This could involve scaling, normalizing, or encoding
variables.
DATA SUMMARIZATION:
Summarization entails calculating key statistics like mean, median,
and standard deviation to understand the data's central tendencies
and variability
FEATURE SELECTION:
In predictive modeling, this step involves choosing the most
relevant variables (features) that contribute to a model's predictive
accuracy

8. THE ITERATIVE NATURE OF EDA:
EDA is an ongoing process. As you uncover insights or face
new questions, you may need to revisit previous steps,
making EDA iterative and flexible.

9. WHY EDA MATTERS IN
STATISTICAL MODELING
9
 Foundational Role of EDA
• The foundational role of Exploratory Data Analysis (EDA) can be
compared to the fundamental support structure of a building
• forms the base upon which all subsequent data analysis and
statistical modeling activities are built.
• EDA is the process of understanding your data, uncovering its
characteristics, and spotting important patterns and trends.
• EDA provides the stability and structure needed for the rest of the
data analysis and modeling process, ultimately leading to accurate
and trustworthy results.

10.  Data Quality Assessment
• It is the process of evaluating the reliability, accuracy, and consistency
of a dataset
• It involves identifying and addressing data issues that could affect the
validity and effectiveness of any analysis or modeling performed on
that data.
• data quality assessment ensures that the data you work with is clean
and reliable.
• Data quality assessment is a critical step because it helps identify and
rectify data issues before you embark on data analysis or modeling
1 0

11.  Understanding Data Characteristics:
oData Distribution: involves examining how data points are spread
across different values. It helps to identify the shape of the distribution,
whether it's normal, skewed, or exhibits other patterns. This insight is
valuable for selecting appropriate statistical models.
oCentral Tendencies: refers to measures that describe the center or
midpoint of a dataset. Common central tendency measures include the
mean (average), median (middle value), and mode (most frequent
value). Knowing these values provides insights into where most data
points are concentrated.
oVariations: Variations in data describe how individual data points
deviate from the central tendency. Variability is often measured by
standard deviation or variance. Understanding variations helps assess
data consistency and potential outliers.
1 1

12. o Relationships Between Variables: Understanding how different
variables relate to each other is vital in EDA. It involves identifying
correlations, dependencies, or patterns between variables, which can
guide the selection of appropriate modeling techniques.
o Data Outliers: Outliers are data points that significantly deviate from the
typical pattern in the dataset. Identifying and understanding outliers is
essential, as they can influence model performance and should be
carefully handled during data analysis.
o Data Trends: Detecting trends over time or across different categories
can provide valuable insights. Trends may reveal seasonality, growth
patterns, or cyclical behavior, depending on the dataset.
1 2

13.  HYPOTHESIS TESTING IN EDA FOR
STATISTICAL MODELING:
it is a fundamental statistical technique used in EDA to assess
the validity of assumptions, make inferences, and determine
whether observed patterns in data are statistically significant.
It is based on two fundamental principles of statistics
 NORMALIZATION
a common method for normalizing data is called min-max scaling.
Xnormalized =
𝑋 −𝑋𝑚𝑖𝑛
𝑋𝑚𝑎𝑥 −𝑋𝑚𝑖𝑛
1 3

14.  Standard normalization
 it is a technique used to transform data into a standard scale
where the mean is 0, and the standard deviation is 1.
Z =
𝑋−𝜇
𝜎
1 4
PRESENTATION
TITLE

15. 1 5
 Steps in hypothesis testing
Formulating Hypotheses: formulating null hypotheses about the data. These
hypotheses can relate to the presence of patterns, relationships, or differences within
the data.
Collecting and Preparing Data: After formulating hypotheses, data is collected and
prepared for analysis. This includes data cleaning, handling missing values, and
organizing the data for hypothesis testing.
Selecting Significance Levels: The level of significance is the degree of importance
with which we are either accepting or rejecting the null hypothesis.generally it is 0.05 or
5%.
Performing Hypothesis Tests: then perform appropriate hypothesis tests, such as t-
tests, chi-squared tests, ANOVA,Z-test. The results of these tests indicate whether the
observed data supports or rejects the null hypothesis.
Interpreting Results: Based on the results of hypothesis tests, draw conclusions about
the data. They may find evidence to support their hypotheses, which can lead to
actionable insights or guide further analyses. Alternatively, they may reject the

16. KEY TECHNIQUES AND
VISUALIZATIONS
1 6
 Histograms:
they are used to visualize the distribution of a single numeric
variable. They display the frequency of data points within specific
ranges along the numeric scale. Histograms help you understand
the central tendency, spread, and shape of the data's distribution.
This Photo by Unknown Author is licensed under CC BY

17. Scatter Plots:
Scatter plots are used to visualize the relationship between two
numeric variables. Each data point is represented by a point on the
graph, making it suitable for examining correlations, patterns, and
trends between two variables.
1 7
This Photo by Unknown Author is licensed under CC BY-SA

18.  Box Plots
they provide a graphical summary of the distribution of a numeric
variable or multiple variables. They display the median, quartiles, and
potential outliers in the data. Box plots are valuable for identifying
skewed data, central tendencies, and variations
1 8
This Photo by Unknown Author is licensed under CC BY-SA

19.  Heatmaps:
They are used to display data in a matrix format, where colors
represent the magnitude of values. They are particularly helpful for
visualizing the relationships between variables in a dataset, especially
in correlation matrices.
1 9
This Photo by Unknown Author is licensed under CC BY-SA

20. REAL-LIFE EXAMPLE: PREDICTING
HOUSE PRICES WITH EDA
Data Collection:
Gather data on various properties, including features like square footage, number of
bedrooms, neighborhood, and recent sale prices.
2. Data Cleaning:
Remove duplicate listings, handle missing data (e.g., if square footage is missing for a
property), and correct data entry errors.
3. Univariate Analysis:
Create histograms to visualize the distribution of sale prices. This helps identify the
typical price range.
4. Bivariate Analysis:
Use scatter plots to explore the relationship between square footage and sale price.
Visualize how price varies with the size of the property.
2 0

21.  Feature Engineering:
Create a new feature, "price per square foot," to standardize price based on property
size. This may reveal insights.
 Correlation Analysis:
Calculate correlations between features and sale prices. Identify which features have
the strongest relationship with house prices.
 Data Visualization:
Generate box plots to visualize how the neighborhood impacts house prices. This
helps identify neighborhoods with higher or lower median prices.
 Hypothesis Testing:
Conduct hypothesis testing to validate if houses with a swimming pool are significantly
more expensive than those without and assist clients in buying or selling homes at
competitive prices
2 1

22. CONCLUSION
In conclusion, we've explored the fundamental role of
Exploratory Data Analysis (EDA) in the area of
statistical modeling. EDA serves as the foundation for
successful data analysis and modeling, enabling us
to uncover valuable insights and make informed
decisions
2 2

23. THANK YOU