linear algebra

2.  ‘크기와 방향을 갖는 성분’
 물리학적 의미
 벡터공간(vector space)의 원소
 Vector space?

3.  𝑉가 8가지 조건이 만족되면 𝑉를 벡터공간이라 한다.
 덧셈에 대한 항등원 존재
 덧셈에 대한 역원 존재
 교환법칙 성립
 결합법칙 성립
 𝑎 ⋅ 𝑢 + 𝑣 = 𝑎 ⋅ 𝑢 + 𝑎 ⋅ 𝑣
 𝑎 + 𝑏 ⋅ 𝑣 = 𝑎 ⋅ 𝑣 + 𝑏 ⋅ 𝑣
 𝑎𝑏 ⋅ 𝑣 = 𝑎 ⋅ 𝑏 ⋅ 𝑣
 1 ⋅ 𝑣 = 𝑣
 3가지만 확인하자
 0이 있는지, 덧셈과 곱셈에 닫혀있는지

4.  ℝ 𝑛
 연속함수의 집합
 다항식의 집합

5.  수, 기호, 수식 등을 네모 꼴에 배열한 것
 행렬의 응용
 연립일차방정식의 풀이
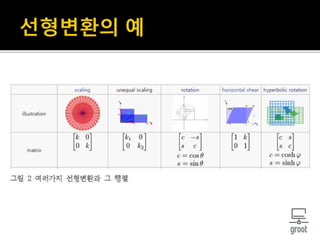
 선형변환

6.  𝑇 ∶ 𝑉 → 𝑊 , 𝑉 𝑎𝑛𝑑 𝑊 𝑎𝑟𝑒 𝑣𝑒𝑐𝑡𝑜𝑟 𝑠𝑝𝑎𝑐𝑒𝑠.
 𝑇 𝑢 + 𝑣 = 𝑇 𝑢 + 𝑇 𝑣
 𝑇 𝑎𝑣 = 𝑎𝑇(𝑣)
 위 두 조건을 만족하는 T를 선형변환이라 한다.
 𝑉가 ℝ 𝑛
과 동치이고 𝑊가 ℝ 𝑚
과 동치일때
 함수 𝑇는 𝑛 × 𝑚행렬로 표현이 가능하다.

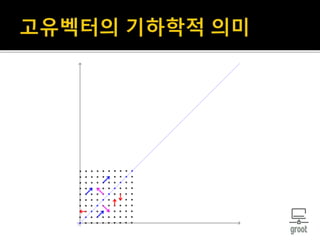
8.  벡터공간 𝑉위에 선형변환 𝑇 ∶ 𝑉 → 𝑉가 주어졌다고 하자.
 𝑣 ∈ 𝑉에 대해 𝑣가 영벡터가 아니고
 𝑇𝑣 = 𝜆𝑣를 만족하면 𝑣를 𝑇의 고유 벡터라 하고,
 𝜆를 𝑣에 대응하는 고유값이라고 한다

10.  Orthogonal matrix
 𝐴 𝑇
𝐴 = 𝐴𝐴 𝑇
= 𝐼
 Diagonalizable
 A 𝑠𝑞𝑢𝑎𝑟𝑒 𝑚𝑎𝑡𝑟𝑖𝑥 𝐴 𝑖𝑠 𝑠𝑎𝑖𝑑 𝑡𝑜 𝑏𝑒 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍𝒊𝒛𝒂𝒃𝒍𝒆 𝑖𝑓 𝑖𝑡 𝑖𝑠 𝑠𝑖𝑚𝑖𝑙𝑎𝑟 𝑡𝑜 𝑠𝑜𝑚𝑒
𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥; (∃ 𝑎𝑛 𝑖𝑛𝑣𝑒𝑟𝑡𝑖𝑏𝑙𝑒 𝑚𝑎𝑡𝑟𝑖𝑥 𝑃 𝑠. 𝑡. 𝑃−1
𝐴𝑃 𝑖𝑠 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙)
 Orthogonally diagonalizable
 A 𝑠𝑞𝑢𝑎𝑟𝑒 𝑚𝑎𝑡𝑟𝑖𝑥 𝐴 𝑖𝑠 𝒐𝒓𝒕𝒉𝒐𝒈𝒐𝒏𝒂𝒍𝒍𝒚 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍𝒊𝒛𝒂𝒃𝒍𝒆 𝑖𝑓 𝑡ℎ𝑒𝑟𝑒
𝑒𝑥𝑖𝑠𝑡𝑠 𝑎𝑛 𝑜𝑟𝑡ℎ𝑜𝑔𝑜𝑛𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥 𝑄 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡 𝑄 𝑇 𝐴𝑄 = 𝐷 𝑖𝑠 𝑎 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥.
 Theorem
 𝐼𝑓 𝐴 𝑖𝑠 𝑎𝑛 𝑛 × 𝑛 𝑚𝑎𝑡𝑟𝑖𝑥, 𝑡ℎ𝑒𝑛 𝑡ℎ𝑒 𝑓𝑜𝑙𝑙𝑜𝑤𝑖𝑛𝑔 𝑎𝑟𝑒 𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡.
▪ 𝐴 𝑖𝑠 𝒐𝒓𝒕𝒉𝒐𝒈𝒐𝒏𝒂𝒍𝒍𝒚 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍𝒊𝒛𝒂𝒃𝒍𝒆.
▪ 𝐴 ℎ𝑎𝑠 𝑎𝑛 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 𝑠𝑒𝑡 𝑜𝑓 𝑛 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟𝑠.
▪ 𝐴 𝑖𝑠 𝒔𝒚𝒎𝒎𝒆𝒕𝒓𝒊𝒄

11.  해결책
feature selection
- selection
feature extraction
- constructing new feature space

12.  차원을 낮춘다(d-dim → k-dim)
 Dataset의 정보를 요약한다.
 많은 양의 데이터를 저장하고 분석하는데
도움(속도, 효율성)

13.  PCA for unsupervised data compression
 LDA, supervised dimensionality reduction
 Kernel principal component analysis
 SVD, Singular Value Decomposition

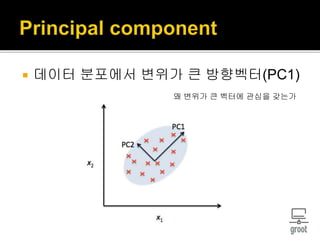
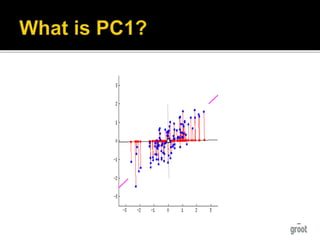
14.  Principal component analysis
 Unsupervised linear transformation
- class label이 없다
 Patterns in data
 Construct d×k matrix
 W : ℝ 𝑑
→ ℝ 𝑘
 d : 원래 차원의 수, k : 줄여진 차원의 수
데이터의 단위가 다르다면 표준화를 한다.

15.  데이터 분포에서 변위가 큰 방향벡터(PC1)
왜 변위가 큰 벡터에 관심을 갖는가

17.  원래 데이터셋(d-features) 에서 orthogonal
unit components를 추출한다.(new bases)
 Variability가 큰 벡터를 찾기
- 거리 유지
 그 축에 맞게 데이터를 새롭게 projection

18. 1. 표준화.
2. 공분산 행렬을 만든다.
3. 그 행렬을 교유벡터, 고유값으로 분해한다.
4. K개의 eigenvector을 고른다.
5. W를 구한다.
6. 변환한다.

19.  Maximize(minimize) f(x) subject to g(x)=0
 𝛻𝑓 𝑥 = 𝜆𝛻𝑔(𝑥)

20.  X는 각 feature에 대해 표준화가 되었다.
- 따라서 평균은 0이고 분산은 1이다.

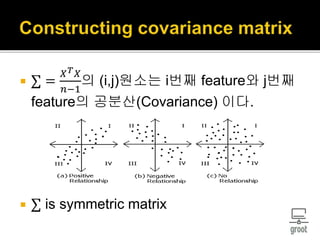
21.  ∑ =
𝑋 𝑇 𝑋
𝑛−1
의 (i,j)원소는 i번째 feature와 j번째
feature의 공분산(Covariance) 이다.
 ∑ is symmetric matrix

22.  Projection onto 𝑒 ∶ 𝑋 𝑒 if ∥ 𝑒 ∥2
= 1.
 𝑉𝑎𝑟 𝑋 𝑒 =
1
𝑛−1
∑(𝑋 𝑒 − 𝐸 𝑋 𝑒 )2
= 𝑒 𝑇
∑ 𝑒
 Maximize 𝑉𝑎𝑟 𝑋 𝑒 𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 ∥ 𝑒 ∥2
= 1
 ∑ 𝑒 = 𝜆 𝑒 𝐵𝑦 𝐿𝑎𝑔𝑟𝑎𝑛𝑔𝑒 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑒𝑟
 𝑉𝑎𝑟 𝑋 𝑒 = 𝜆

23. 공분산행렬은 대칭행렬이다.
따라서 공분산행렬은 직교대각화 가능하다.
1. 공분산행렬은 𝑑개의 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙한 고유벡터를 갖는다.
2. 𝐸𝑣𝑒𝑟𝑦 𝑛𝑜𝑛𝑧𝑒𝑟𝑜 𝑓𝑖𝑛𝑖𝑡𝑒 − 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛𝑎𝑙 𝑖𝑛𝑛𝑒𝑟 𝑝𝑟𝑜𝑑𝑢𝑐𝑡 𝑠𝑝𝑎𝑐𝑒
ℎ𝑎𝑠 𝑎𝑛 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 𝑏𝑎𝑠𝑖𝑠.
따라서 유한개의 고유값 중에 상위 𝑑개 𝜆1 ≥ 𝜆2 ≥ ⋯ ≥ 𝜆 𝑑 > 0
를 뽑을 수 있다.

24.  Eigenvalues 𝜆1, 𝜆2, … , 𝜆 𝑑 of ∑ and corresponding eigenvectors
𝑣1, 𝑣2, … , 𝑣 𝑑, ∥ 𝑣𝑖 ∥2
= 1 𝑓𝑜𝑟 𝑖 = 1,2, … , 𝑑
 𝑍 = 𝑋𝑣1 𝑋𝑣2 … 𝑋𝑣 𝑑 = 𝑋𝑉, linear function
 행 별로 관찰 : 정사영
 𝑍𝑖 = [𝑋𝑖 𝑣1 𝑋𝑖 𝑣2 … |𝑋𝑖 𝑣 𝑑]
 열 별로 관찰
 𝑧𝑗 = 𝑋𝑣𝑗
 𝑉𝑎𝑟 𝑧𝑗 = 𝜆𝑗
 𝐶𝑜𝑣 𝑍 = 𝜆𝑖 𝑖𝑓 𝑖 = 𝑗
= 0 𝑂. 𝑊.

25.  V : X → Z, linear transformation을 구함
 Cov(Z) is a diagonal matrix
 차원을 감소시키진 않았다.

26.  Z에서 𝜆𝑖가 크다는 것은 𝑧𝑖의 분산이 큼을 의미
 우리의 목적은 분산이 큰 PC를 구하는 것
 𝑘개의 𝑓𝑒𝑎𝑡𝑢𝑟𝑒를 고를때 분산이 큰 순서로
뽑자
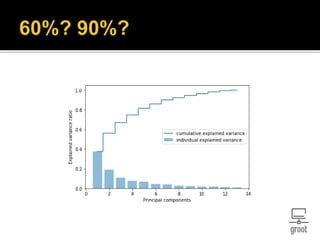
 혹은 전체 데이터의 variance중 90% 만큼 설
명하는 차원까지 감소시키자.
𝑟𝑎𝑡𝑖𝑜 =
𝜆 𝑖
∑𝜆 𝑗

28. 𝑑 − 𝑑𝑖𝑚에서 𝑘 − 𝑑𝑖𝑚으로 줄이기
𝐾 = 𝑣1 𝑣2 ⋯ 𝑣 𝑘 를 만든다.
𝑋 𝑘−𝑑𝑖𝑚
∗
= 𝑋𝐾
끝.

29.  PCA를 ‘비지도 선형변환’이라고 하는 이유
 변환하는데 있어서 class label이 필요 없고, 속
성값에만 의존하기 때문.
 비선형 문제에도 사용할 수 있는가?
 해결책 : KPCA(kernel PCA)