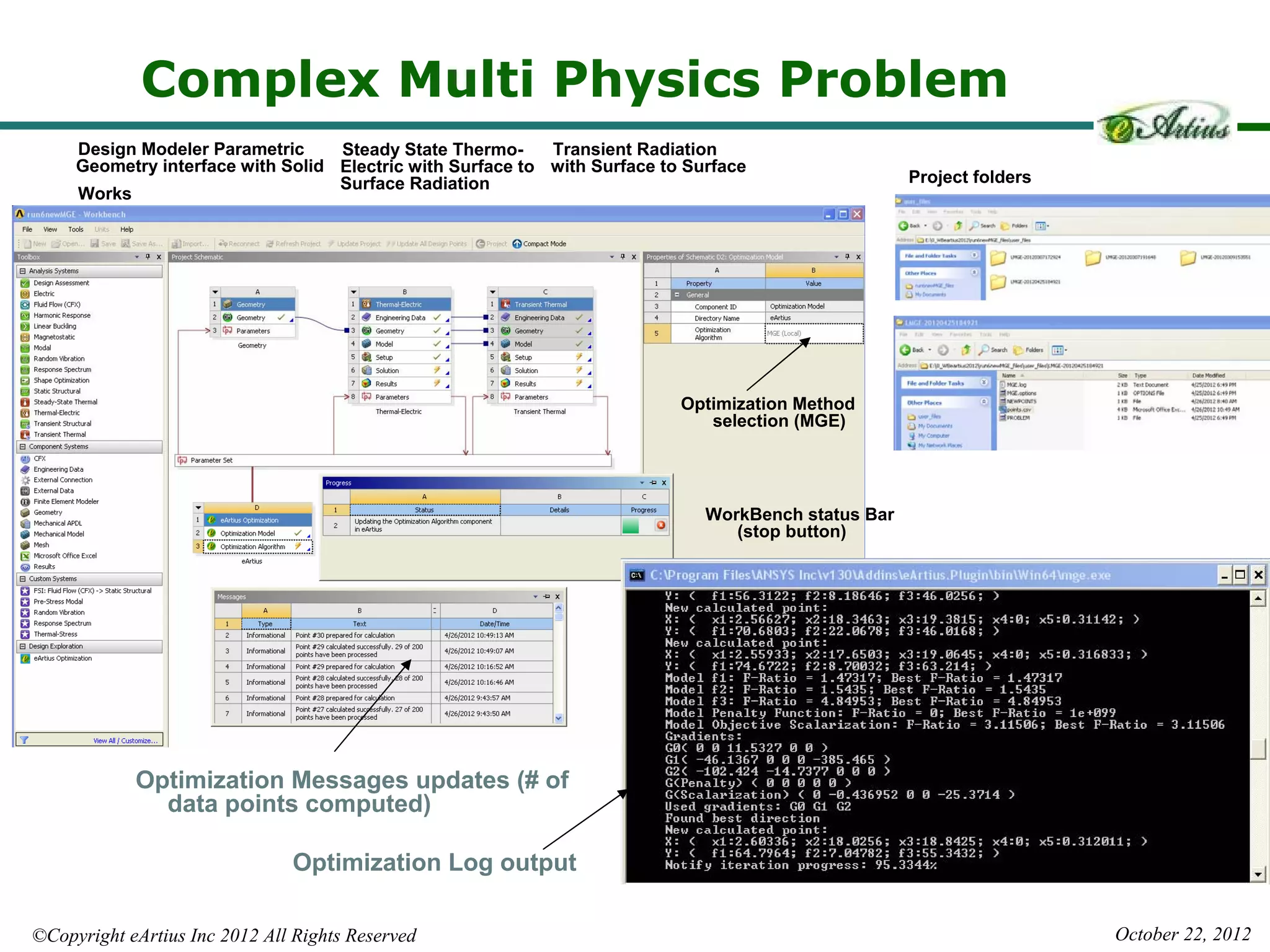
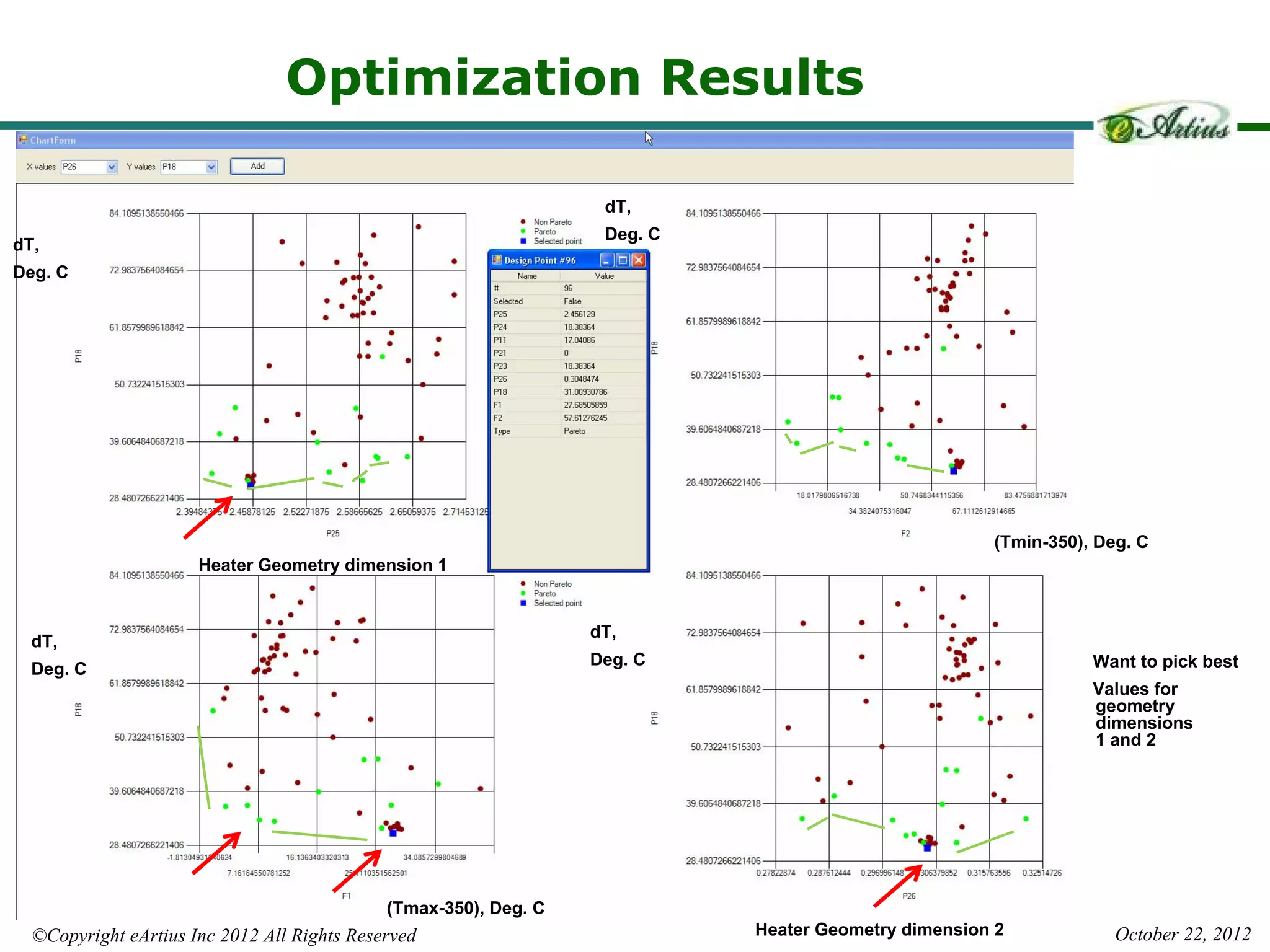
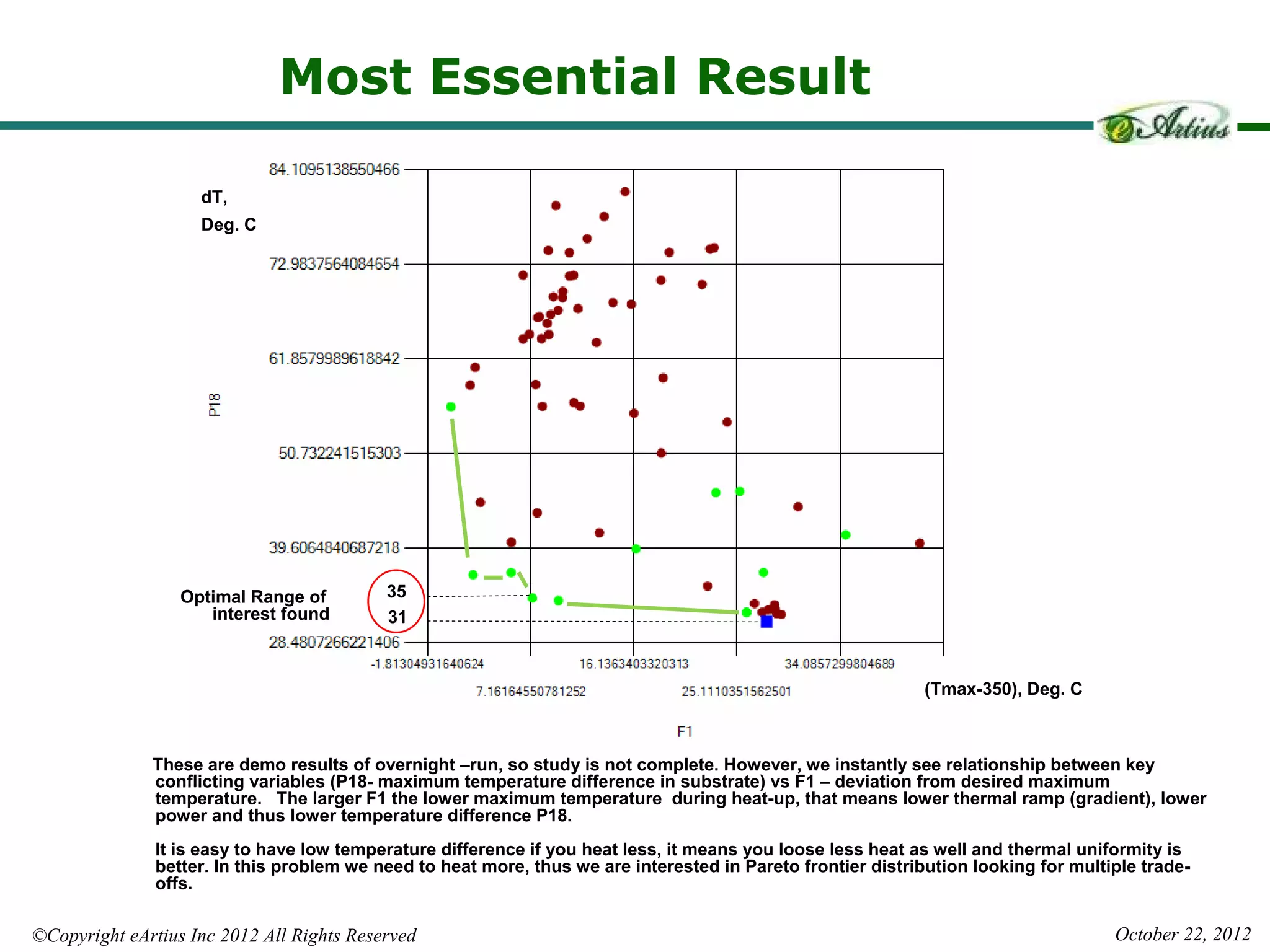
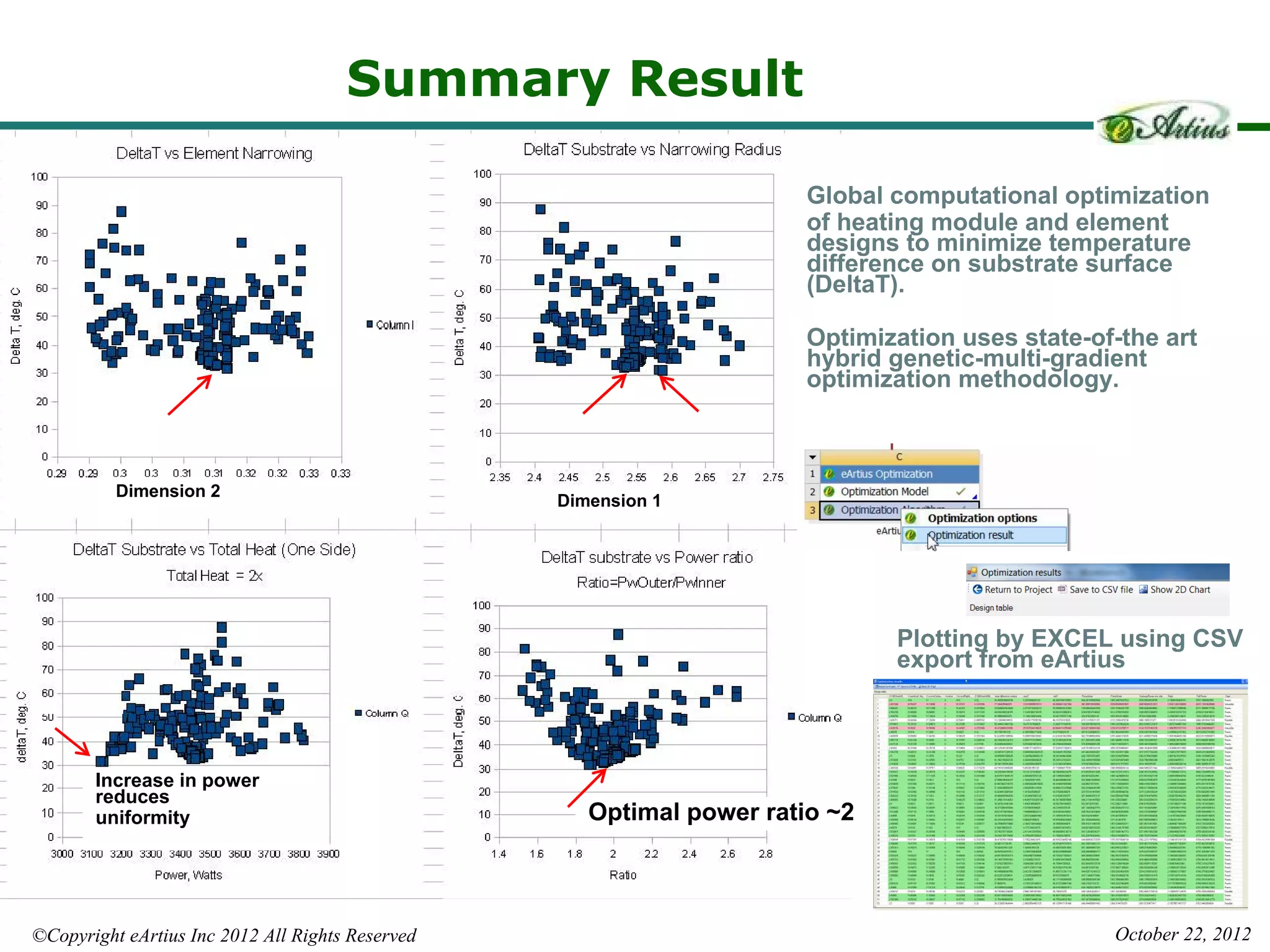
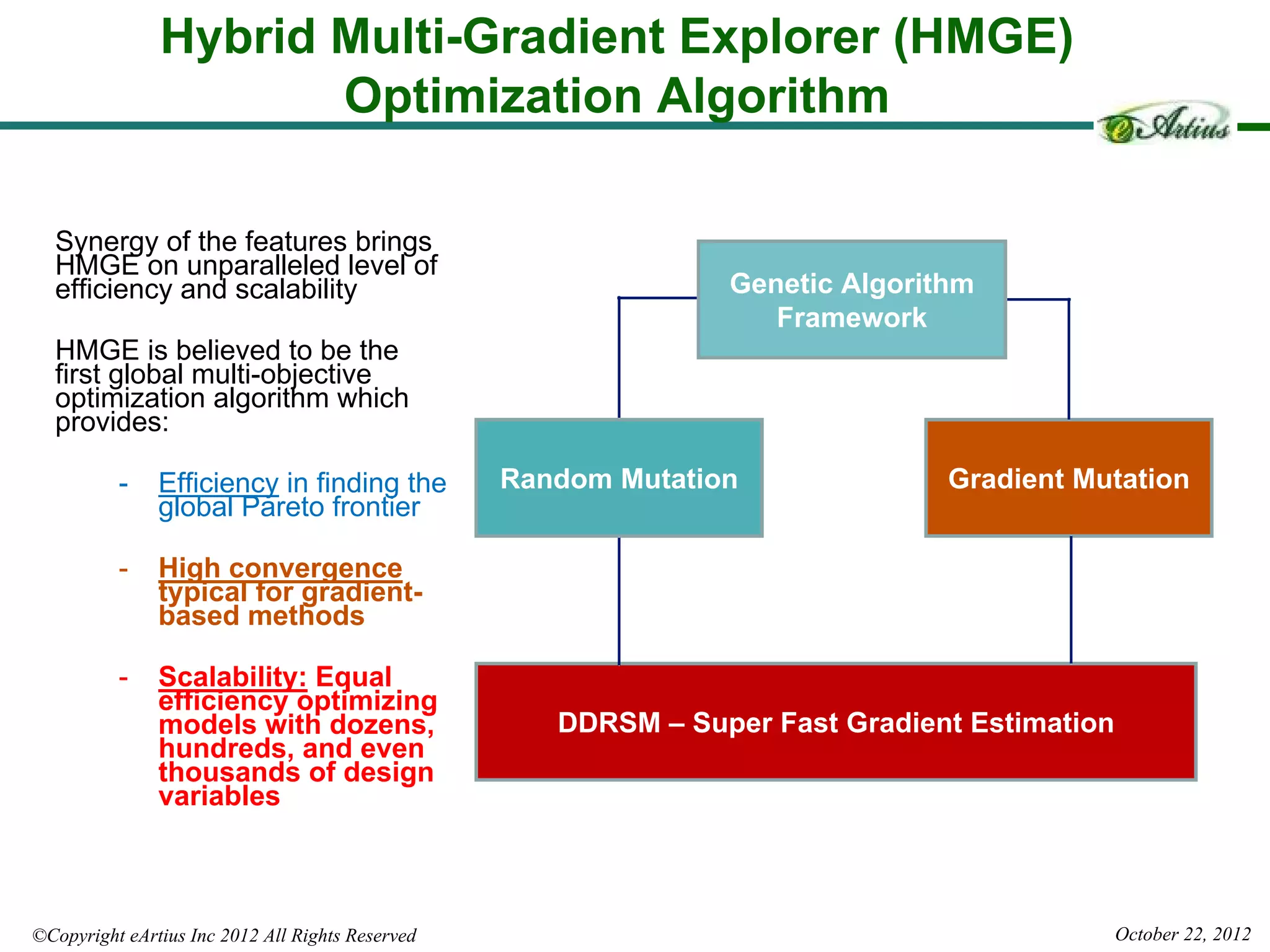
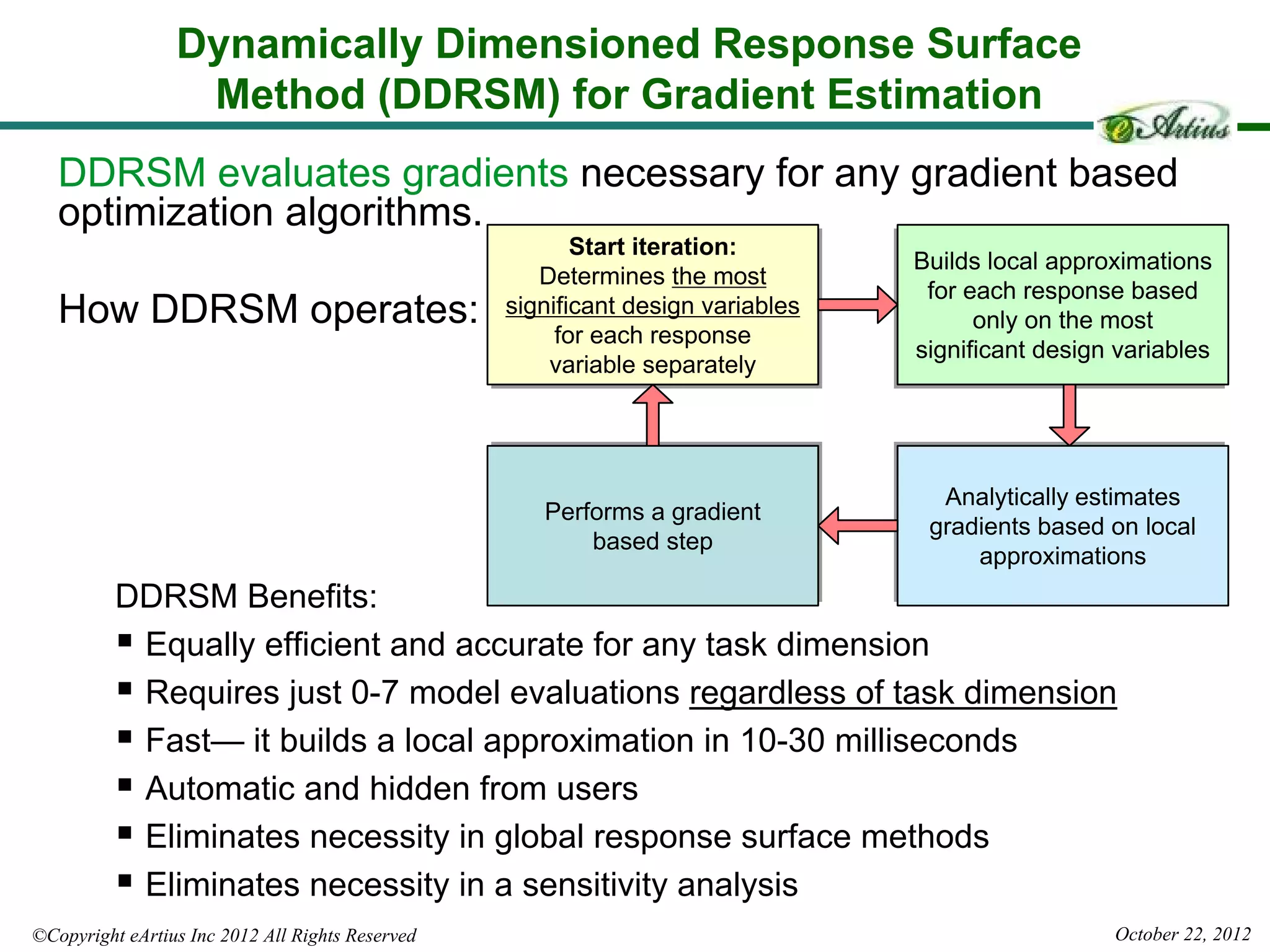
The document outlines Eartius Inc.'s Hybrid Multi-Gradient Explorer (HMGE) optimization algorithm, which efficiently handles optimization tasks with 10,000 design variables and dynamically identifies significant variables. It discusses the algorithm's method of utilizing gradient-based steps to improve convergence and detailing its effectiveness in finding Pareto optimal solutions across various multi-objective problems. Additionally, an applied engineering example demonstrates the algorithm's capability in optimizing complex thermal systems, highlighting its scalability and efficiency in high-dimensional optimization tasks.







![Optimization Results for 7 “Craters”
– 2 objectives to be minimized
– 10,000 design variables with the range [-10, 10]
– 1000 model evaluations
– 53 Pareto optimal solutions
©Copyright eArtius Inc 2012 All Rights Reserved October 22, 2012](https://image.slidesharecdn.com/eartius-highdimension-moo-2-130120201900-phpapp01/75/eArtius-HMGE-Algorithm-Applied-to-Optimization-Tasks-with-10-000-Design-Variables-10-2048.jpg)
![Optimization Results for 8 “Craters”
– 2 objectives to be minimized
– 10,000 design variables with the range [-10, 10]
– 1000 model evaluations
– 97 Pareto Optimal Points
©Copyright eArtius Inc 2012 All Rights Reserved October 22, 2012](https://image.slidesharecdn.com/eartius-highdimension-moo-2-130120201900-phpapp01/75/eArtius-HMGE-Algorithm-Applied-to-Optimization-Tasks-with-10-000-Design-Variables-11-2048.jpg)
![Optimization Results for 10 “Craters”
– 2 objectives to be minimized
– 10,000 design variables with the range [-10, 10]
– 909 model evaluations
– 54 Pareto Optimal Points
©Copyright eArtius Inc 2012 All Rights Reserved October 22, 2012](https://image.slidesharecdn.com/eartius-highdimension-moo-2-130120201900-phpapp01/75/eArtius-HMGE-Algorithm-Applied-to-Optimization-Tasks-with-10-000-Design-Variables-12-2048.jpg)