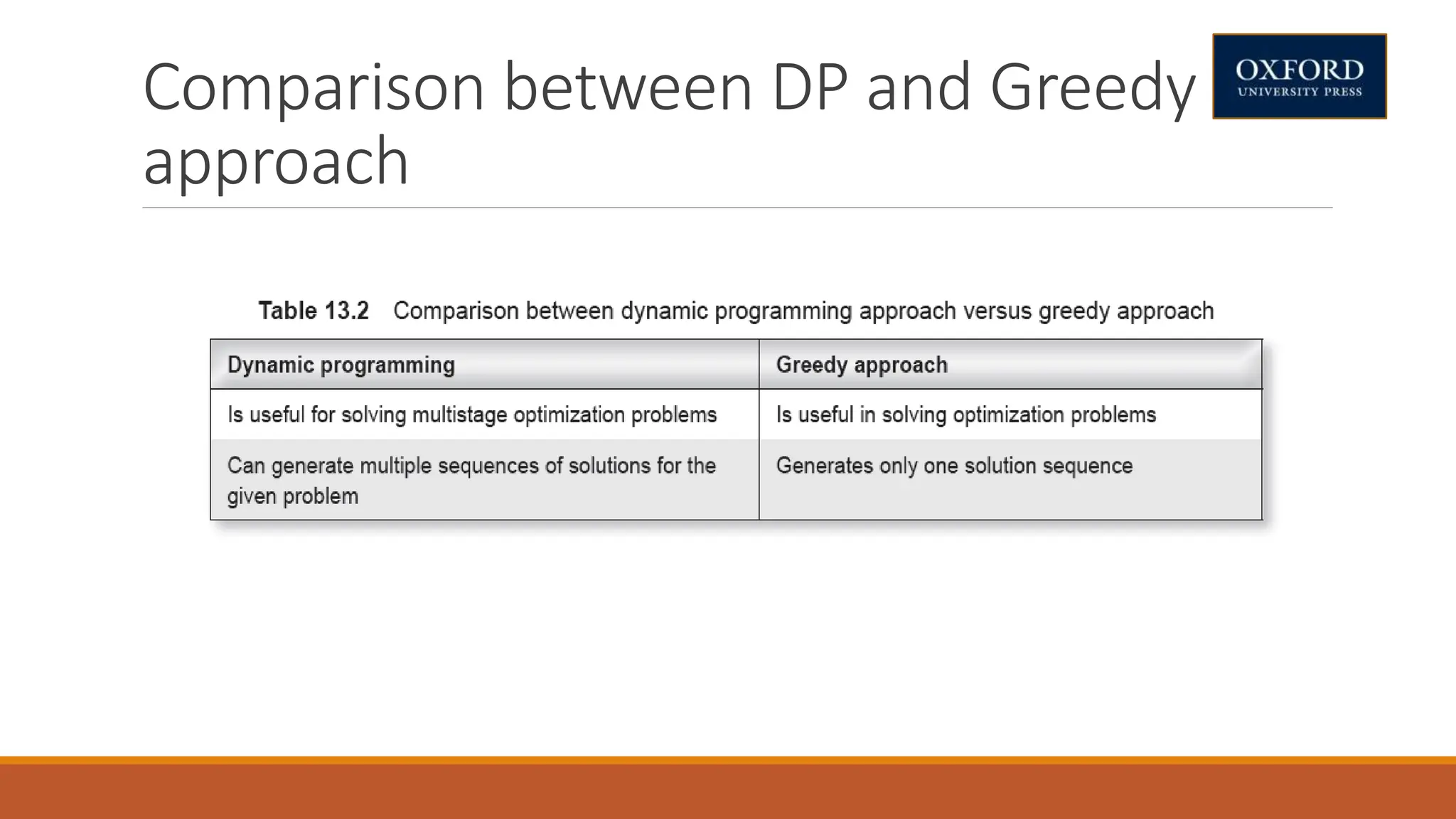
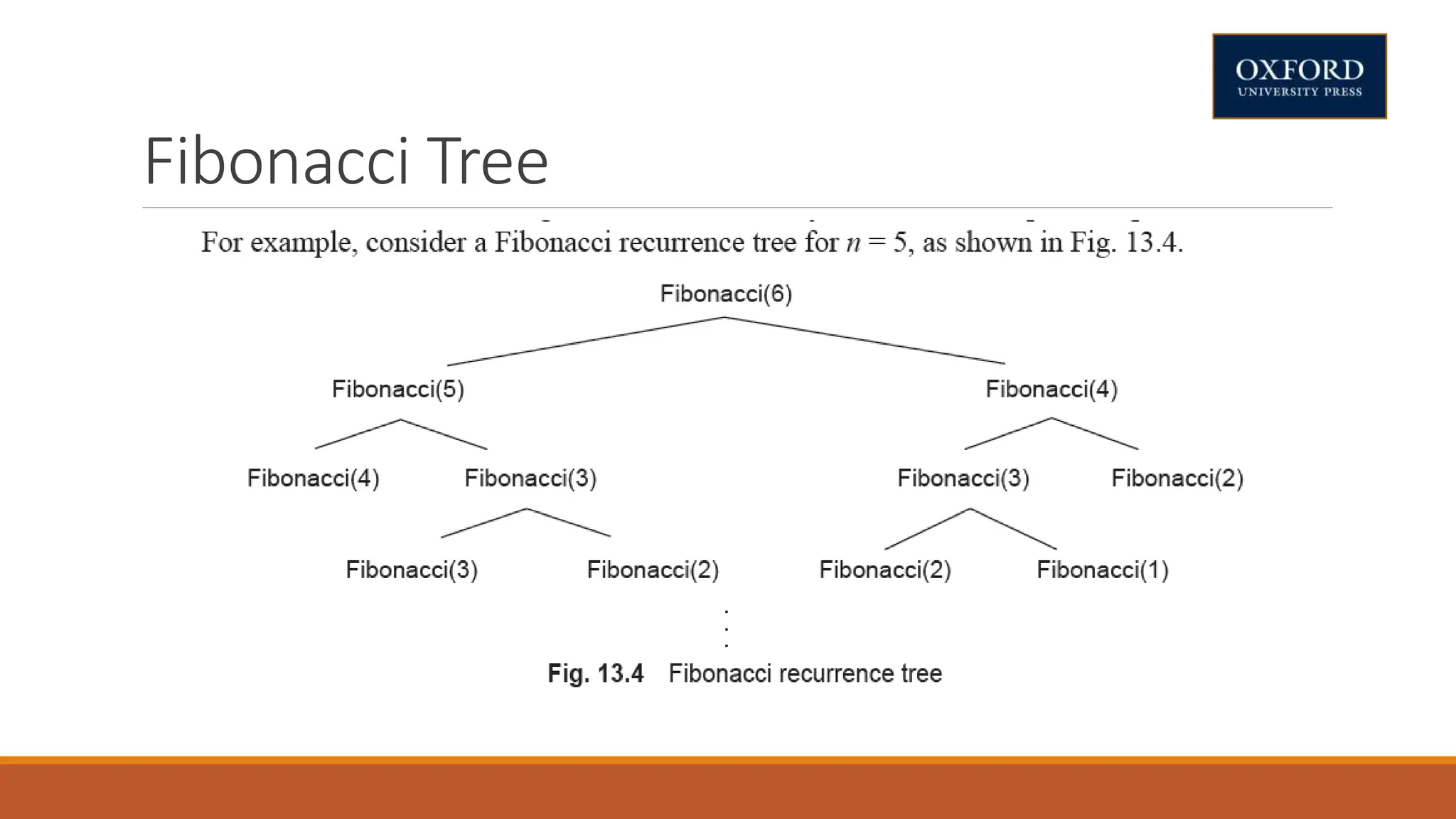
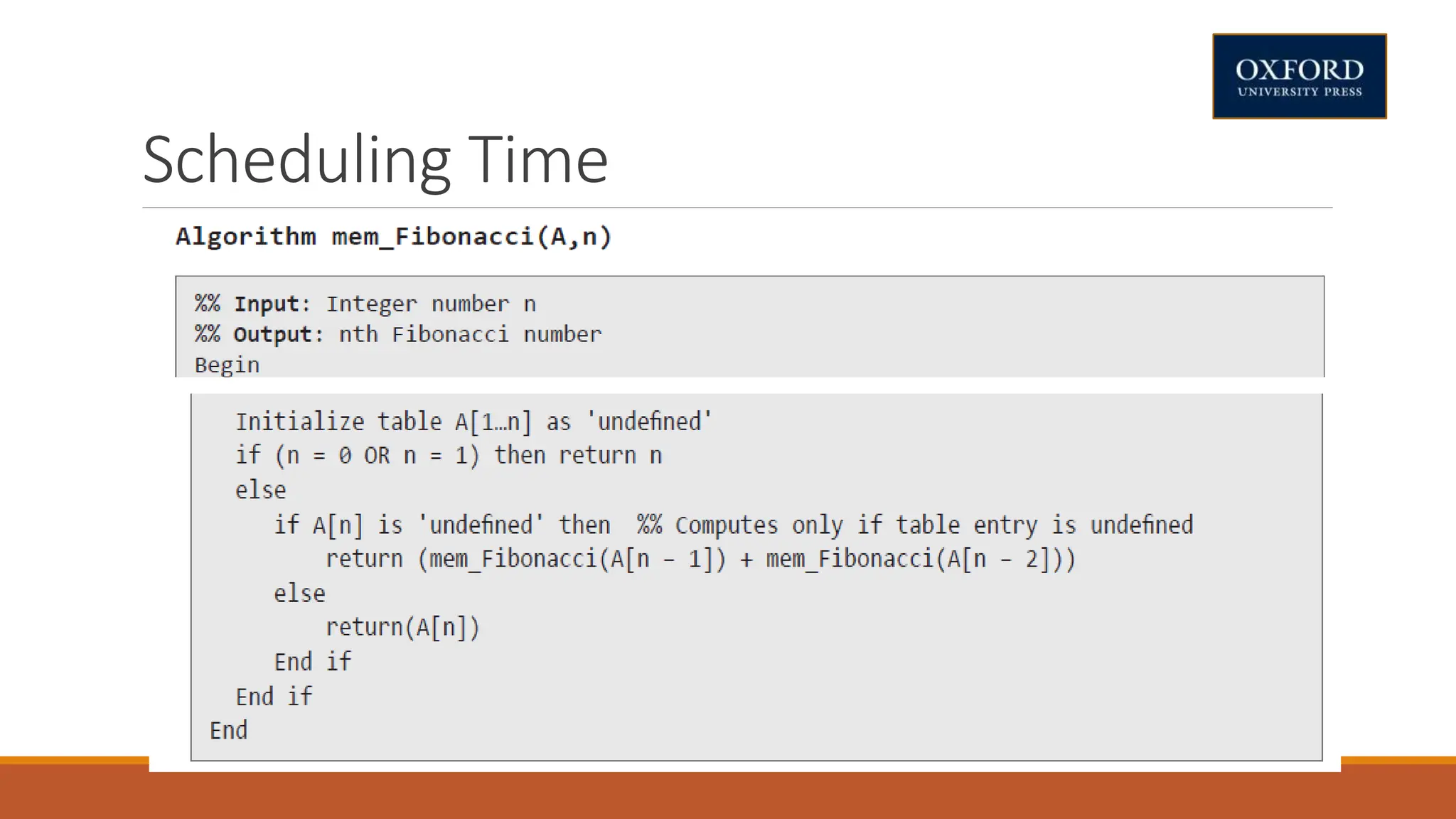
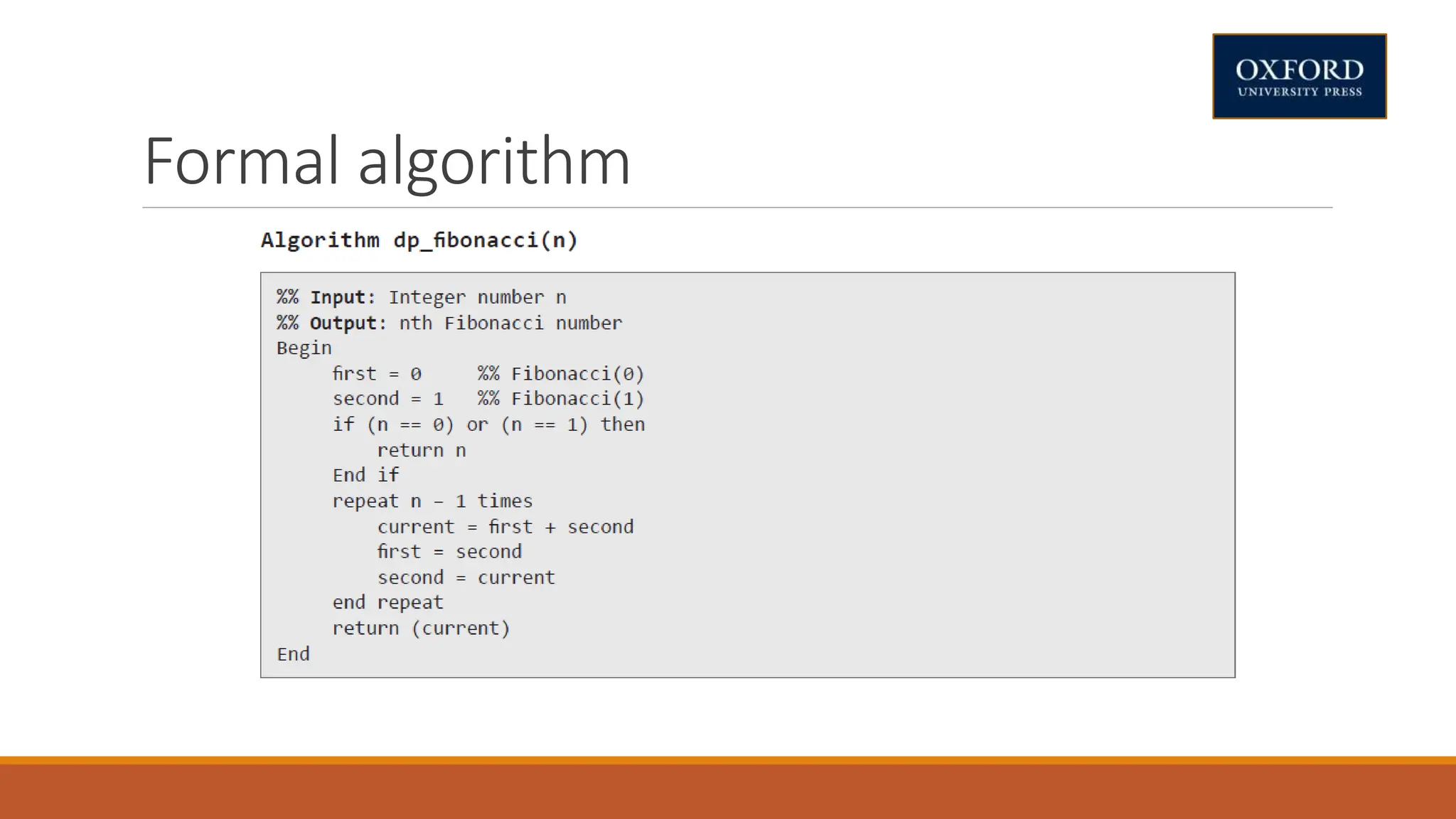
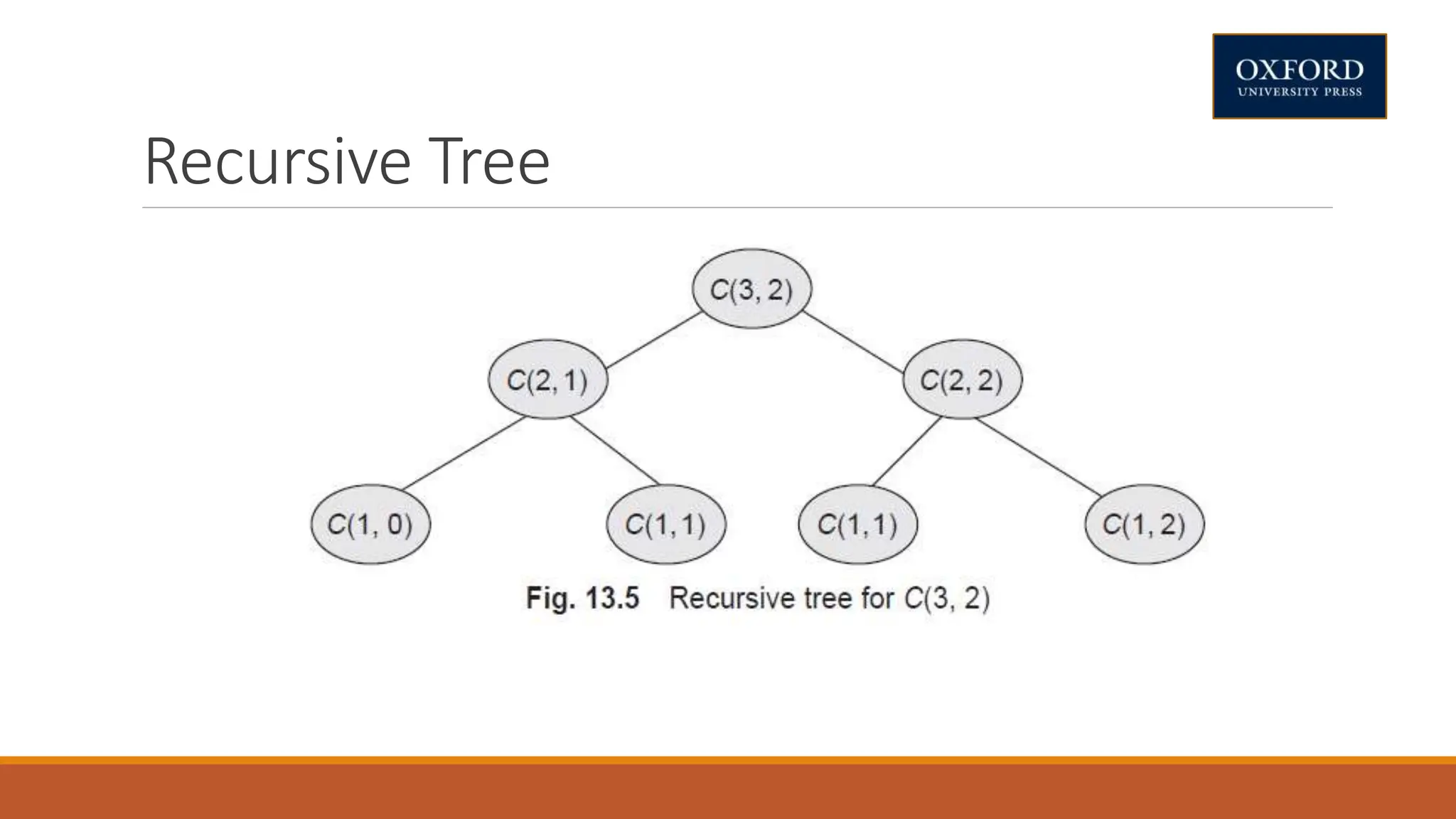
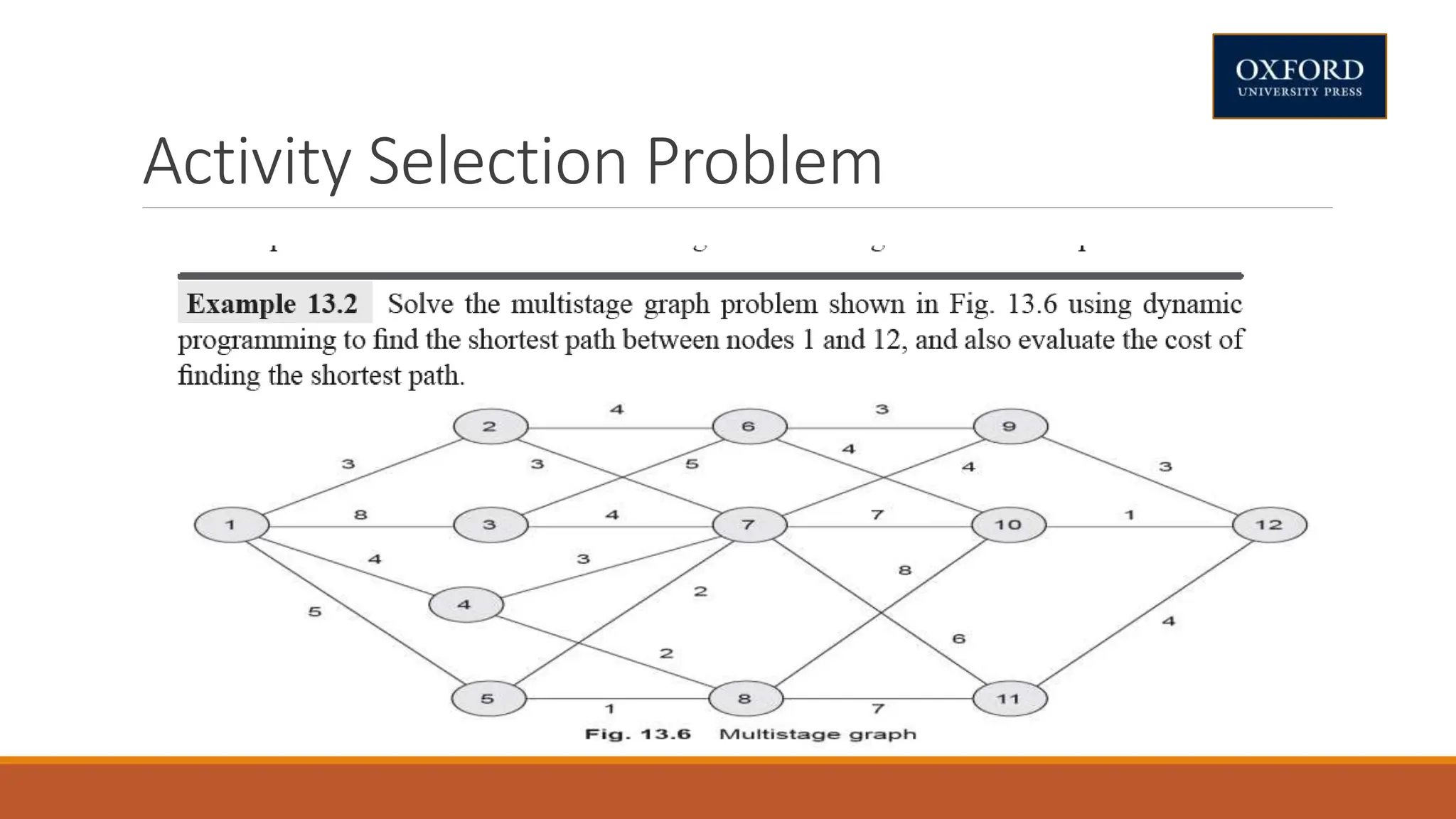
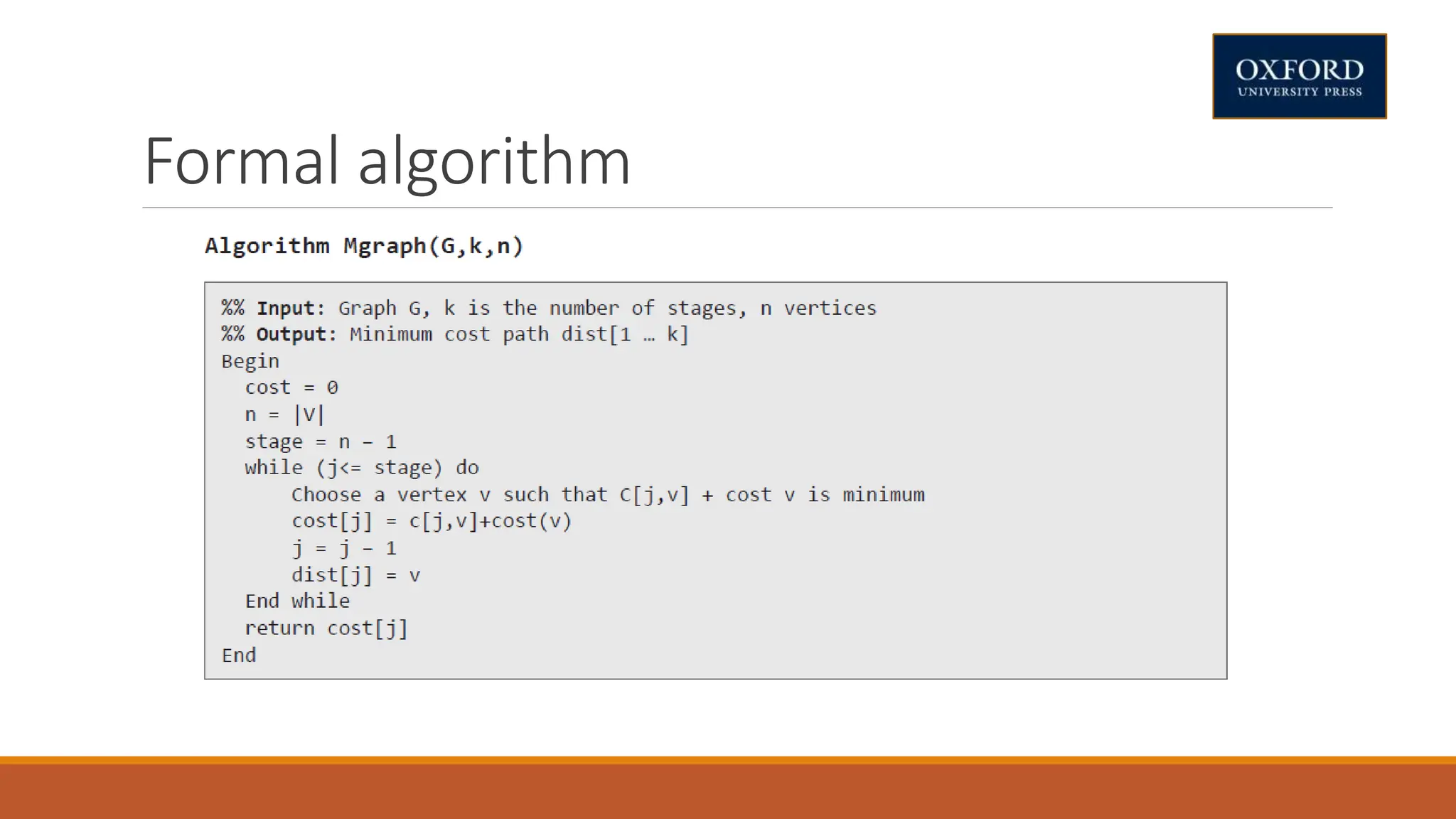
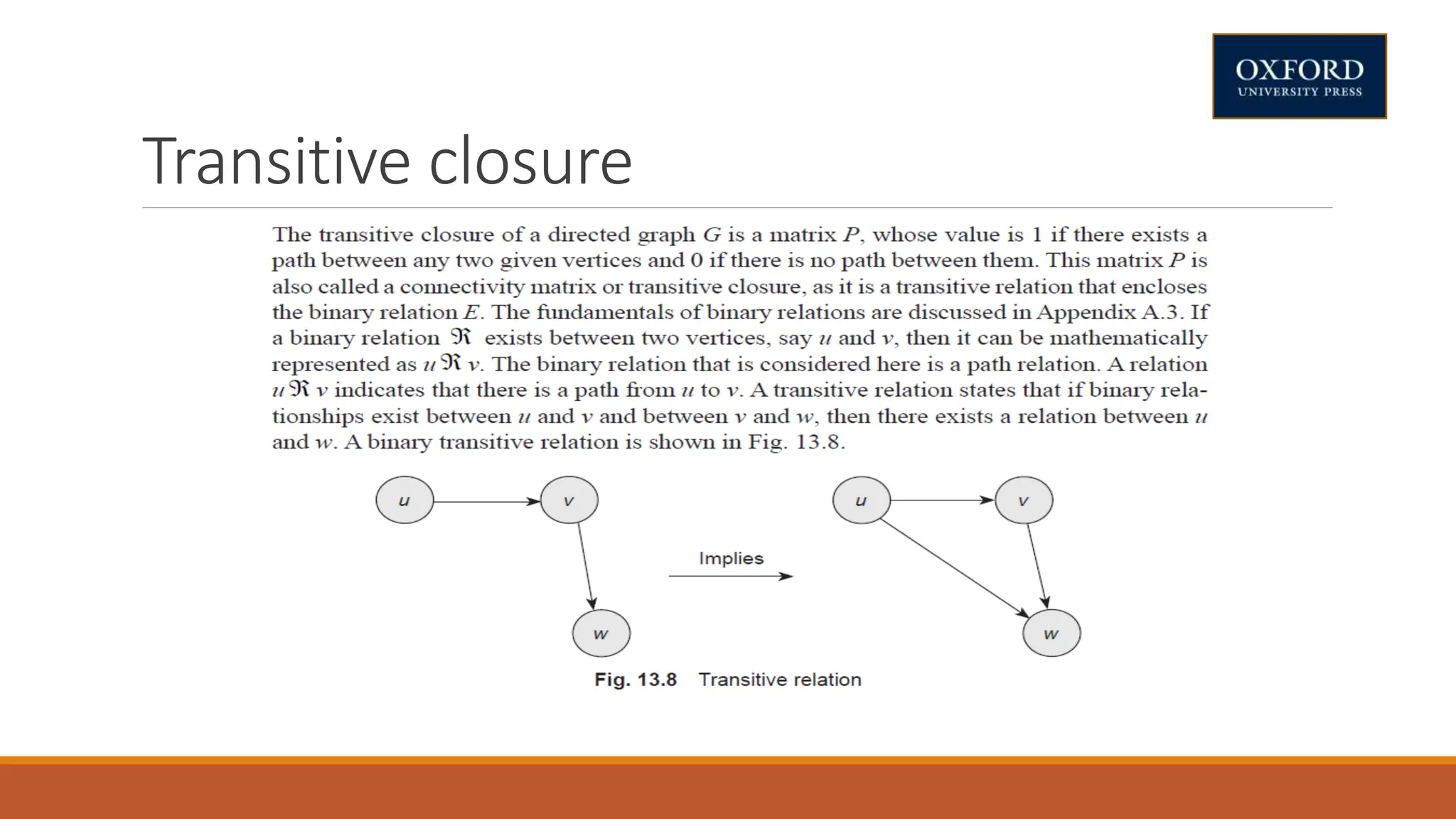
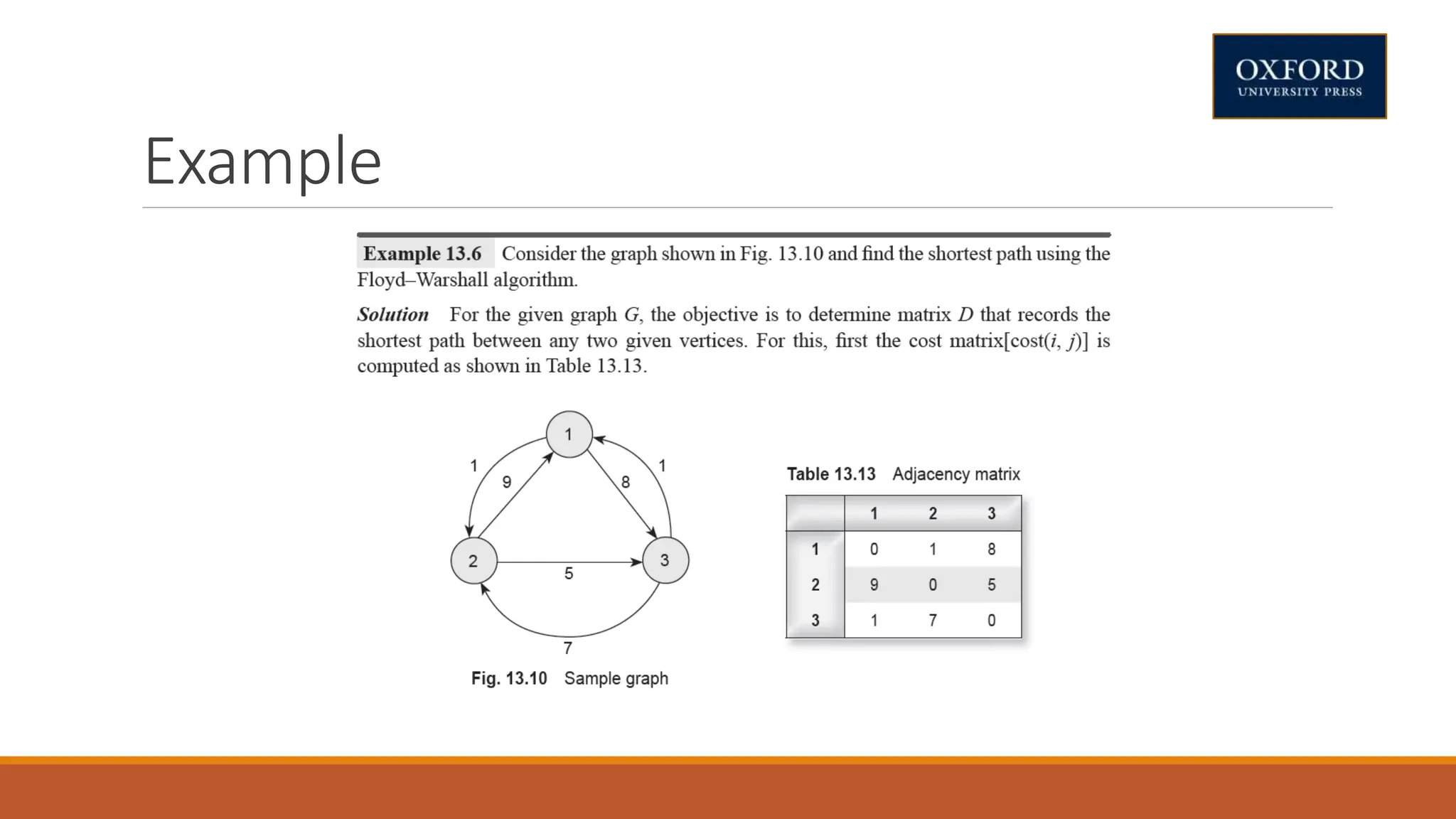
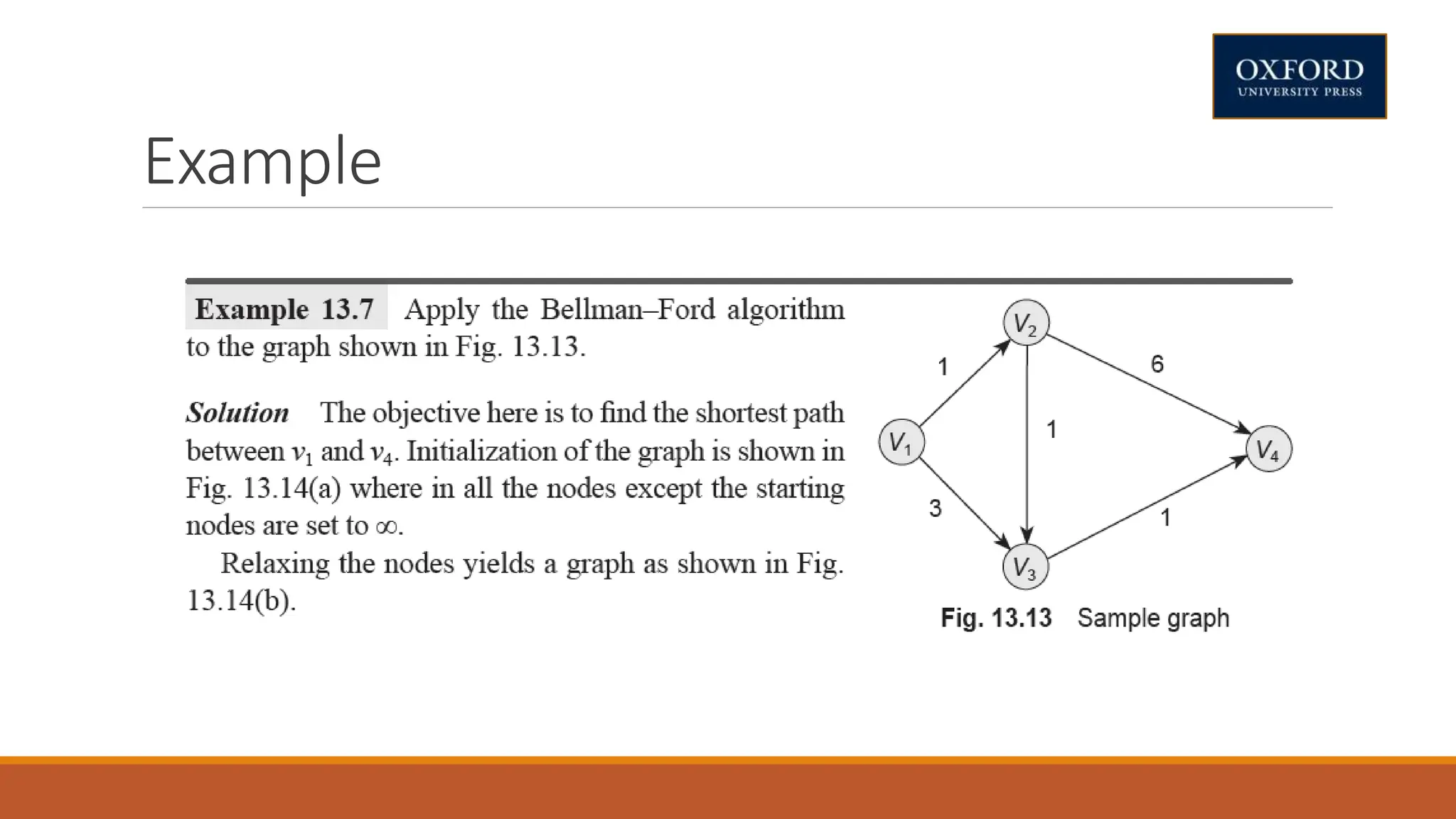
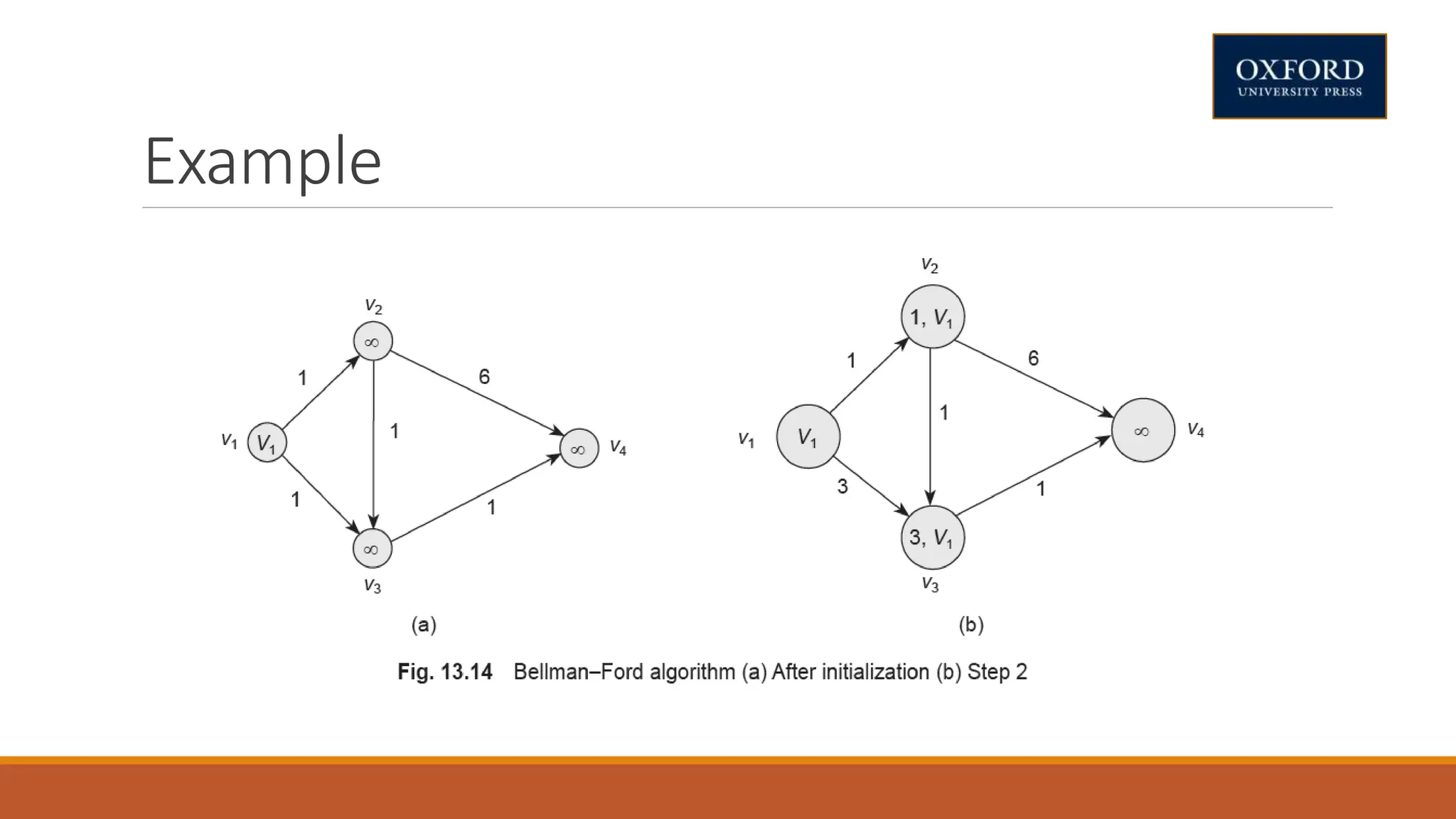
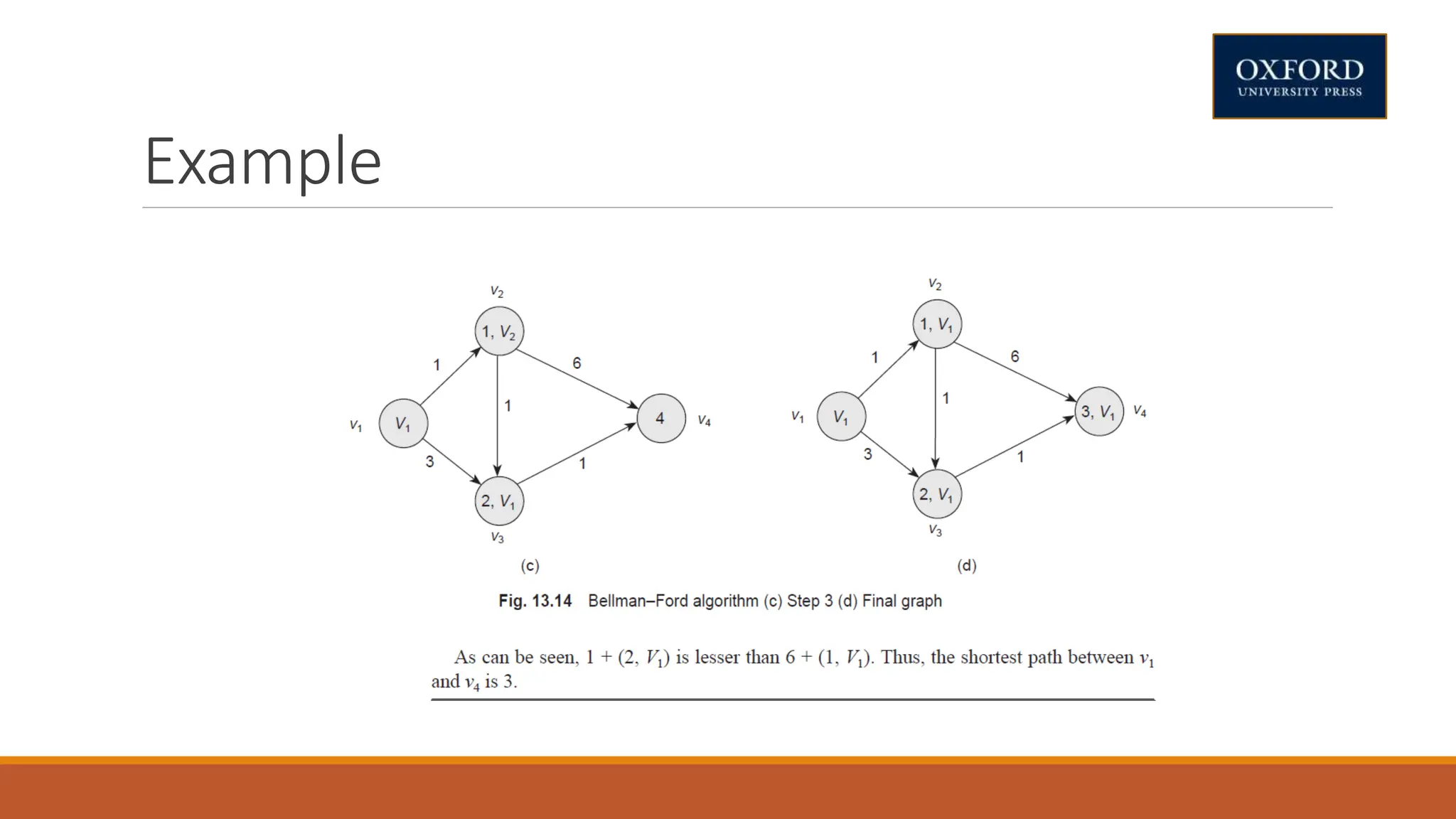
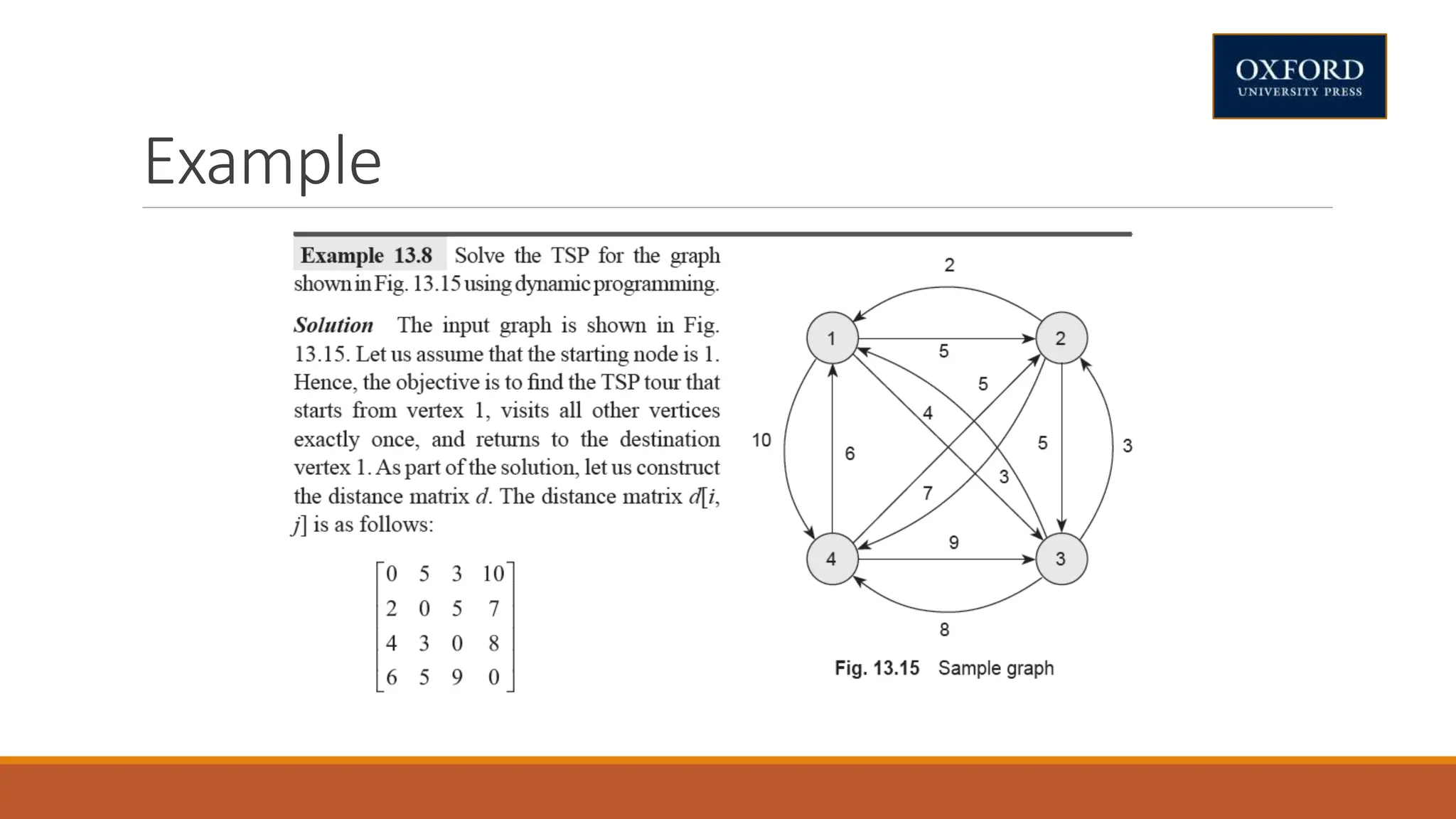
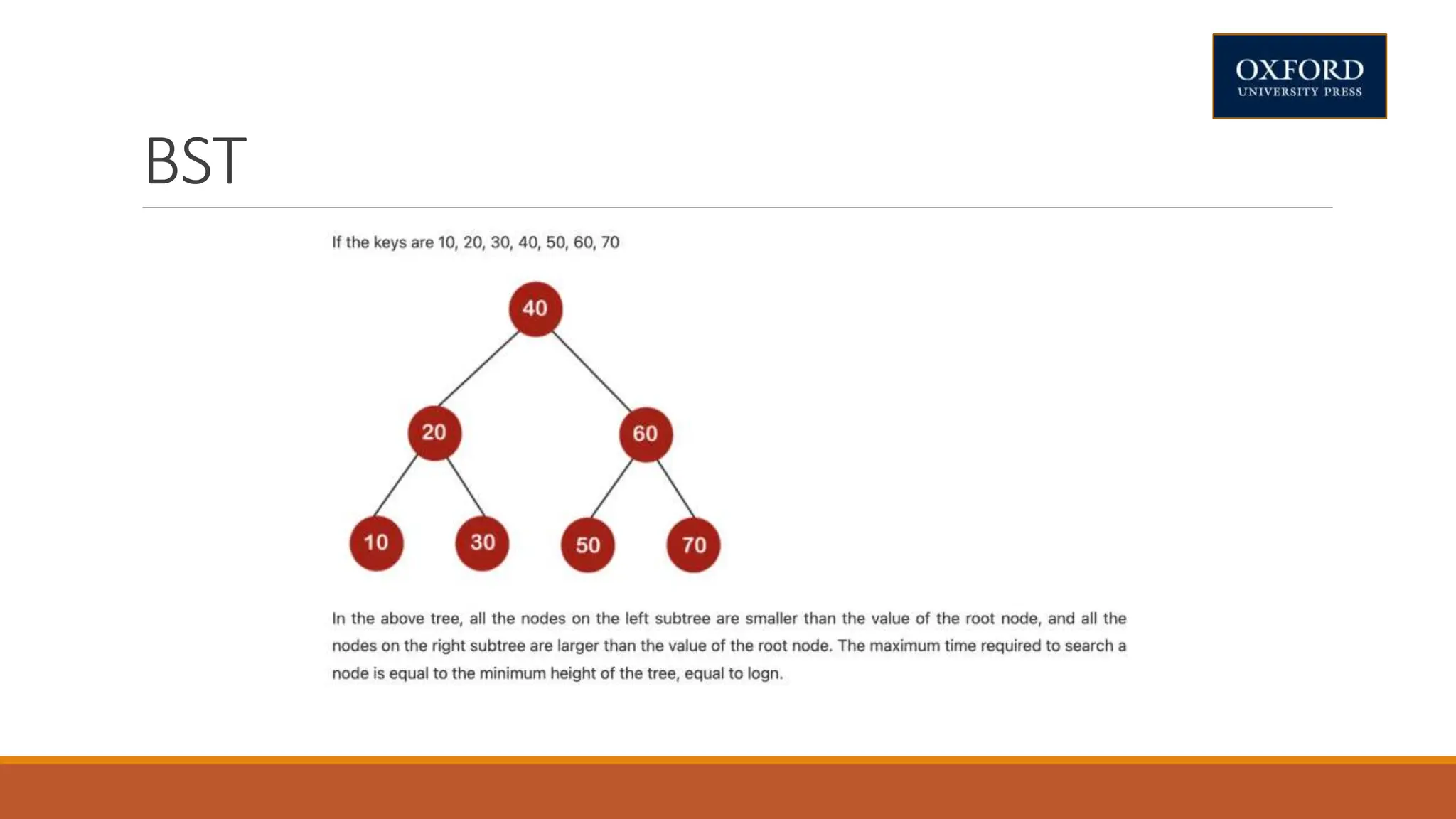
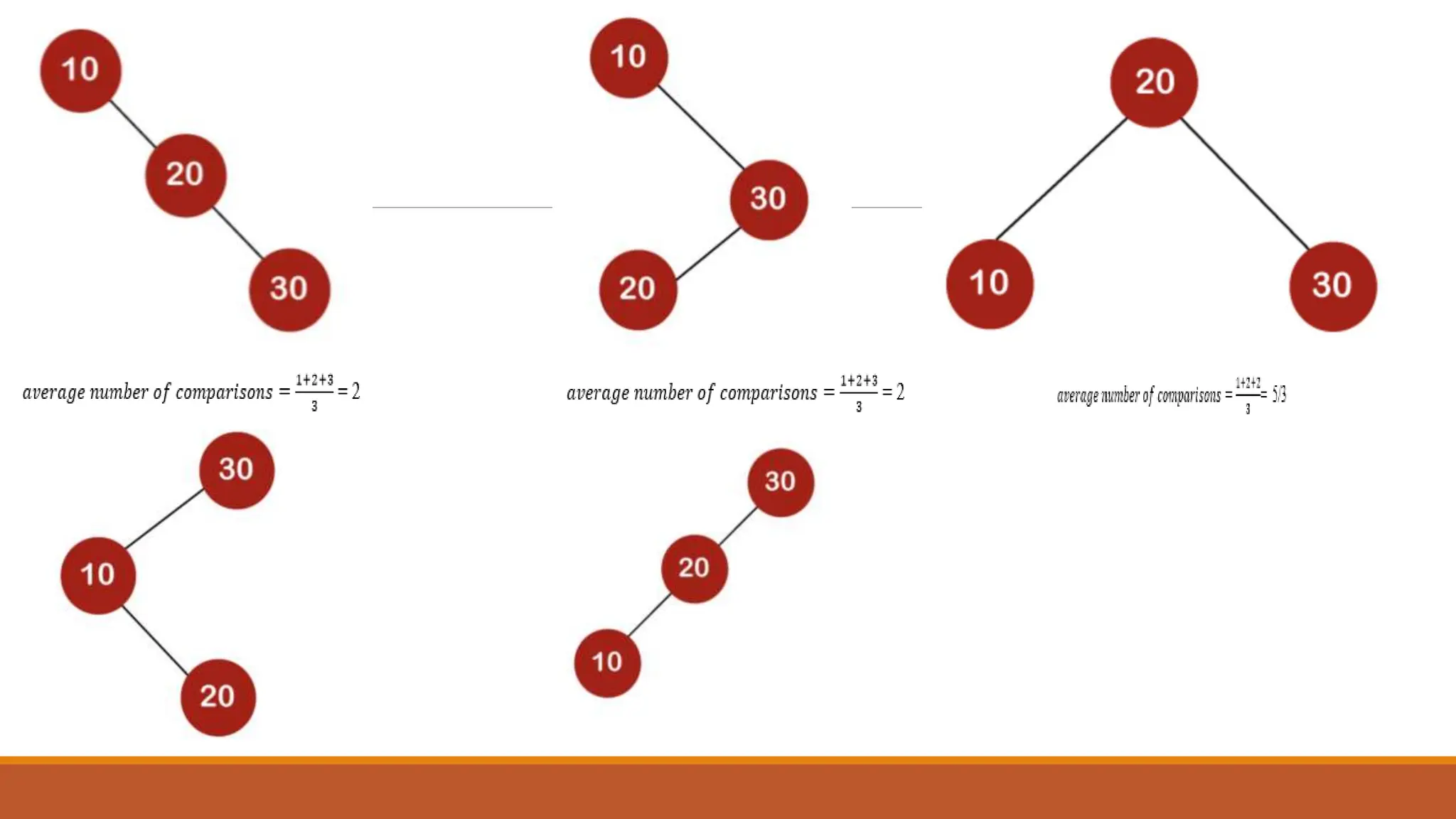
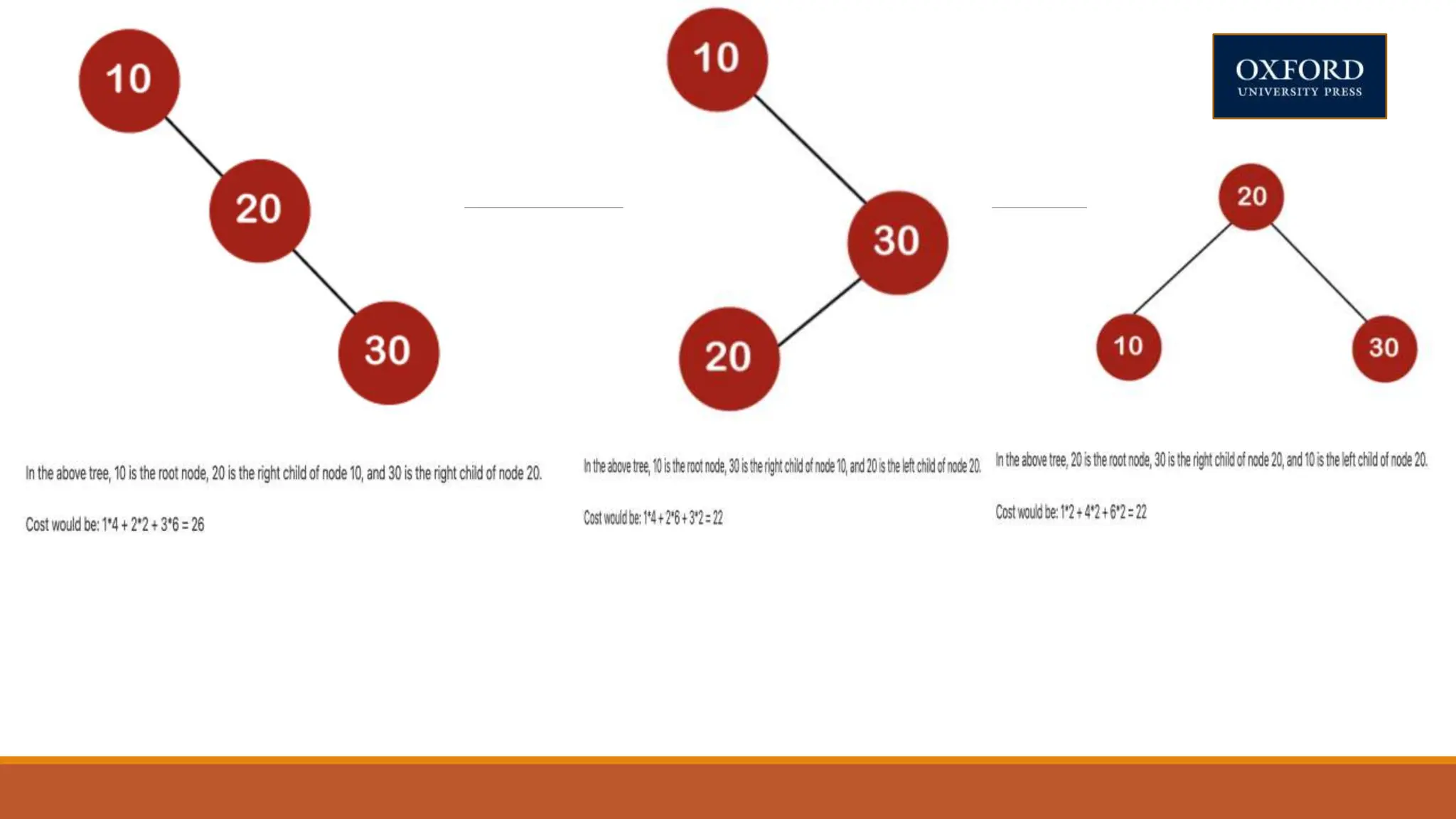
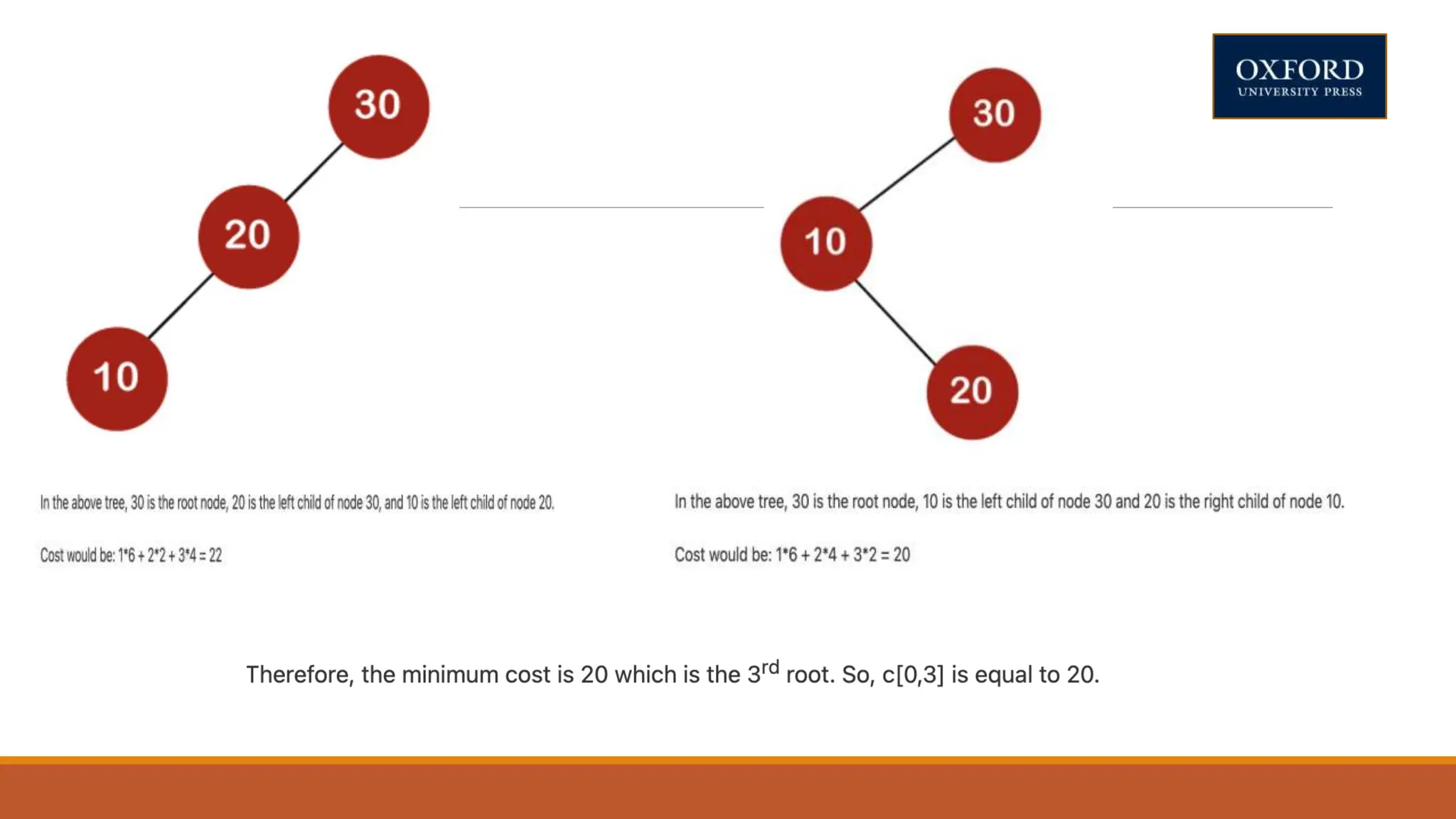
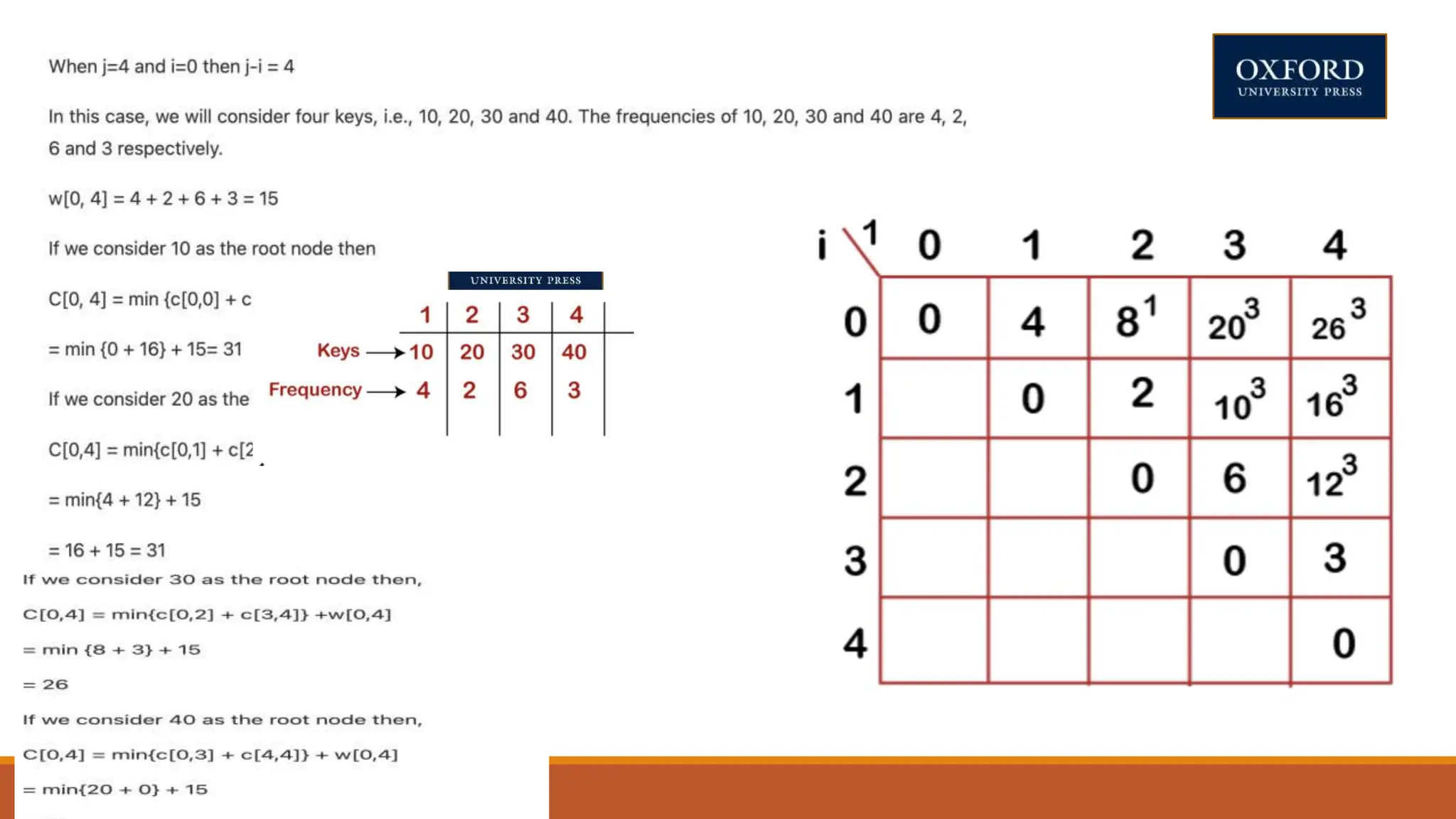
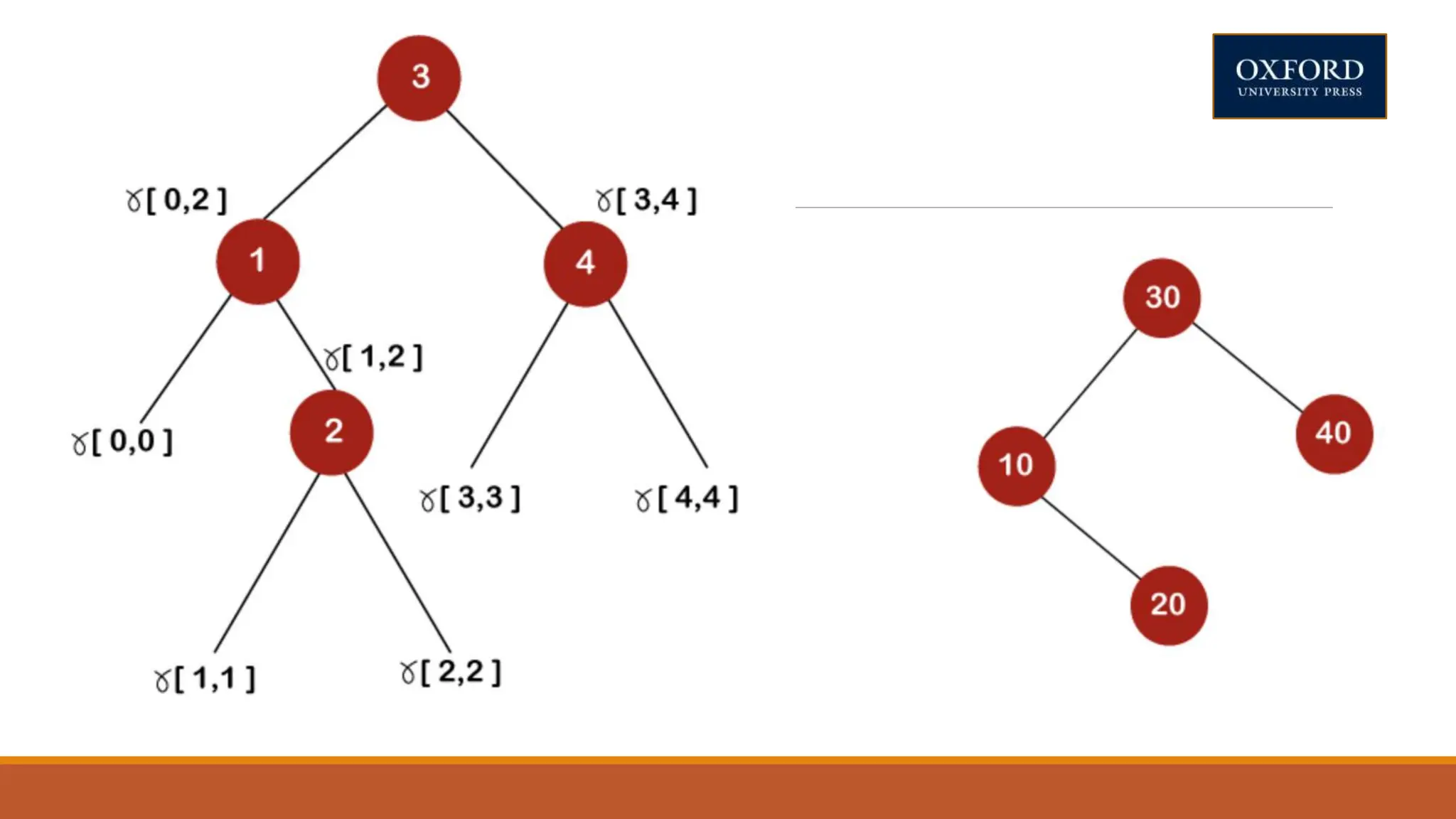
This document covers dynamic programming techniques and algorithms. It discusses topics like the principle of optimality, components of dynamic programming, properties, advantages and disadvantages. It provides algorithms and examples for problems like Fibonacci numbers, binomial coefficients, activity selection, shortest paths, transitive closure, optimal storage, traveling salesperson, chain matrix multiplication, knapsack problem, optimal binary search trees, and flow shop scheduling.

1. Chapter 13: Dynamic
Programming

2. objectives

3. Dynamic Programming

4. Dynamic Programming approach

5. Component of Dynamic Programming
(DP)

6. Components of DP

7. Principle of Optimality

8. Detailed Procedure of DP

9. Forward and Backward Computing
Procedure

10. Properties of DP

11. Properties Contd..

12. Advantages and Disadvantages of DP

13. Comparison between DP and Divide &
Conquer

14. Comparison between DP and Greedy
approach

15. Fibonacci Problem

16. Fibonacci Tree

17. Complexity analysis of Traditional
approach

18. Fibonacci (DP) Approach – Table
approach

19. Scheduling Time

20. Informal modified algorithm

21. Formal algorithm

22. Formal algorithm

23. Complexity Analysis

24. Binomial Coefficient

25. Recursive Tree

26. Formal algorithm

27. Informal algorithm

28. Table

29. Formal algorithm

30. Formal algorithm

31. Complexity analysis

32. Example

33. Multistage Graph Problem

34. Informal algorithm

35. Activity Selection Problem

36. Steps

37. Steps

38. Steps

39. Steps

40. Steps

41. Formal algorithm

42. Formal algorithm for path construction

43. Backward Computation

44. Example

45. Example

46. Example

47. Example

48. Complexity analysis

49. Transitive closure

50. Brute force approach

51. Informal Warshall algorithm

52. Formal algorithm

53. Complexity analysis

54. Example

55. Example

56. Example

57. Example

58. Final conclusion

59. Alternative method

60. Example

61. Formal algorithm

62. Formal algorithm

63. Complexity analysis

64. Example

65. Example

66. Optimal Storage Problem

68. Informal Floyd-Warshall algorithm

69. Example

70. Example

71. Example

72. Example

73. Formal algorithm

74. Formal algorithm

75. Formal algorithm for path construction

76. Complexity Analysis

77. Bellman-Ford algorithm

78. Initialization

79. Relaxation rules

80. Informal algorithm

81. Example

82. Example

83. Example

84. Formal algorithm

85. Complexity analysis

86. Traveling Salesperson Problem

87. Traveling Salesperson Problem

88. Informal algorithm

89. Informal algorithm

90. Example

91. Example

92. Solution

93. Final Solution

94. Final Solution

95. Complexity analysis

96. Chain matrix multiplication

97. Example

98. Dynamic programming formulation

99. Informal algorithm

100. Informal algorithm for optimal order

101. Formal algorithm

102. Complexity analysis

103. Example

104. Example

105. Example

106. Final solution

107. Knapsack Problem

108. Mathematical formulation

109. Informal algorithm

110. Formal algorithm

111. Complexity analysis

112. Example

113. Example

114. Example

115. Example

116. Optimal BST – What is BST?

117. BST

118. OBST

120. Let's assume that frequencies associated with the keys 10, 20, 30 are 3, 2, 5.
The above trees have different frequencies. The tree with the lowest frequency would be considered the
optimal binary search tree. The tree with the frequency 17 is the lowest, so it would be considered as the
optimal binary search tree.
1*3+2*2+3*5=22 1*3+2*5+3*2=19 1*2+2*3+2*5=18
5+6+6=17 5+4+9=18

121. Dynamic Programming Approach

122. First, we will calculate the values
where j-i is equal to zero.

123. Now we will calculate the values
where j-i = 2
20
10

131. Recursive formulation

132. Example

133. Example

134. Example

135. Example

136. Example

137. Final Solution

138. Example

139. Example

140. Formal algorithm

141. Complexity analysis

142. Flow shop scheduling Problem

143. Single machine sequencing problem

144. Terminologies

145. Example

146. Two machine sequence problem

147. Informal algorithm

148. Example

149. Example

150. Example

151. Example

152. Final solution

153. Complexity Analysis

154. Glossary