PUGLIA - DSA e matematica - Imperiale

DISTURBI, DIFFICOLTÀ E…
DINTORNI DELLA MATEMATICA
COME AFFRONTARLI?
Roberto IMPERIALE
(UNIVERSITÀ DELLA VALLE D’AOSTA)

VICEPRESIDENTE NAZIONALE

GRIMeD
GRUPPO RICERCA MATEMATICA e DIFFICOLTÀ
roberto.imperiale@fastwebnet.it
r.imperiale@univda.it
24/11/2011 R. Imperiale, DISCALCULIA 1

UN TESTO DI RIFERIMENTO

A. Biancardi, E. Mariani, M. Pieretti,

LA DISCALCULIA EVOLUTIVA
DAI MODELLI NEUROPSICOLOGICI ALLA RIABILITAZIONE

Franco Angeli, Milano, 2011


Un attore racconta:
- Per una scena del mio ultimo film, il
regista mi aveva chiesto un’espressione
tra il pensieroso e l’inquieto. Ho
cominciato a pensare alla fame nel
mondo, ma non funzionava; allora mi
sono chiesto quanto fa sette per otto: e
così che ho ottenuto la candidatura
all’Oscar.
Dalla Settimana Enigmistica (n° 4152 del 22/10/2011):


DICIAMO SUBITO CHE
1. LA DISCALCULIA
NON RIGUARDA LA MATEMATICA
MA UNA PARTE
ASSAI ESIGUA E STRUMENTALE DI ESSA
IL CALCOLO E I DISTURBI DEL CALCOLO
PERCHÉ LA MATEMATICA NON È IL (SOLO) CALCOLO
E – SOPRATTUTTO -
IL CALCOLO NON È LA MATEMATICA
NÉ IL DISTURBO DEL CALCOLO COINCIDE
CON LE DIFFICOLTÀ DI CALCOLO
2. PER QUESTO LA DISCALCULIA SI MANIFESTA
IN PERCENTUALI ASSAI MODESTE
NELL’UNIVERSO “DISTURBO-DIFFICOLTÀ”

INFATTI, SECONDO L’AIRIPA

ASSOCIAZIONE ITALIANA PER LA RICERCA E L’INTERVENTO
NELLA PSICOPATOLOGIA DELL’APPRENDIMENTO

ESPRIMENDOSI I GRADI DI COMPROMISSIONE DELLE ABILITÀ
LUNGO UN CONTINUUM PRESTAZIONALE

TRA DISTURBO E DIFFICOLTÀ
VIENE ASSUNTO COME PARAMETRO STATISTICO CRITICO
IL 5° PERCENTILE
PERCHÉ
IL DISTURBO PREVEDE UN LIVELLO DI ABILITÀ
INFERIORE AL 5° PERCENTILE
LA DIFFICOLTÀ PREVEDE UN LIVELLO DI ABILITÀ
COMPRESO TRA IL 5° E IL 15° PERCENTILE.


TEST DI VALUTAZIONE

Test di I Livello:
AC-MT (Cornoldi, Lucangeli, Bellina, 2002)
per tutte le classi elementari
↓
fornisce uno screening di base

Test di II Livello:
ABCA (Lucangeli, Tressoldi, Fiore, 1998)
BDE (Biancardi, Nicoletti, 2003)
↓
forniscono profilo di discalculia evolutiva

SECONDO CHRISTINE TEMPLE
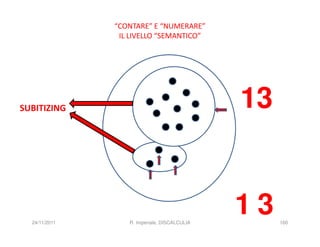
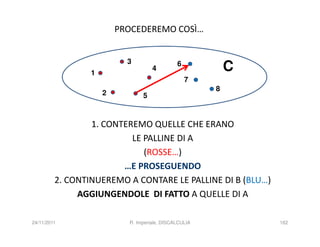
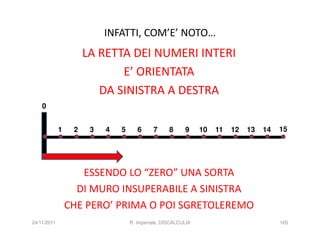
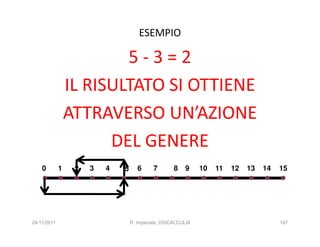
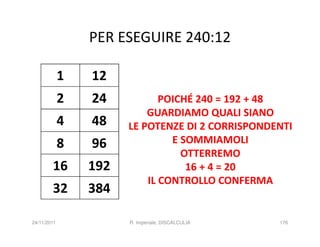
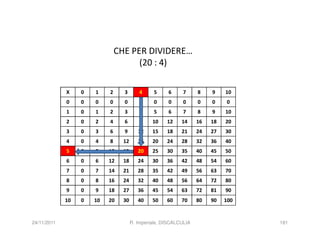
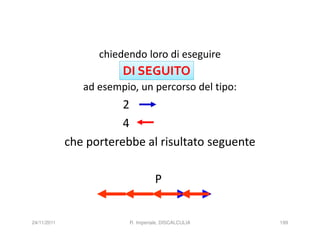
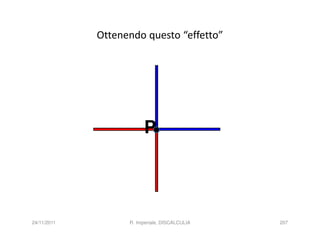
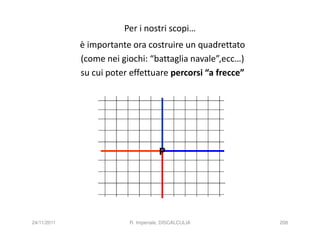
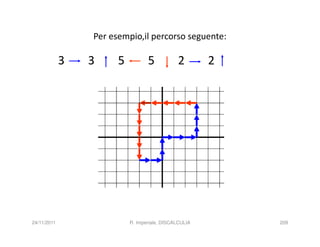
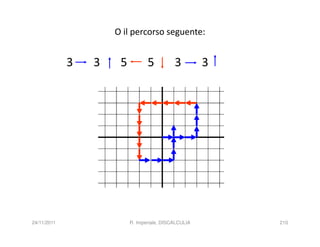
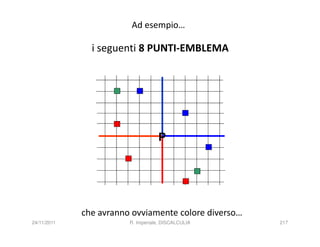
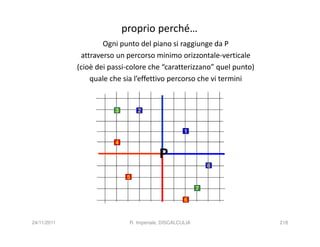
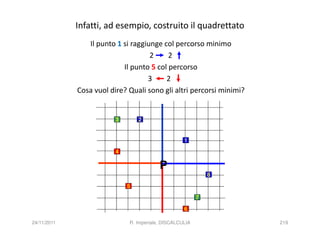
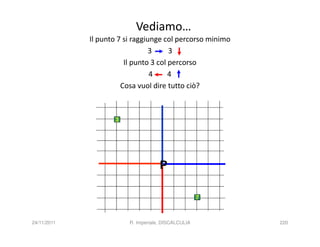
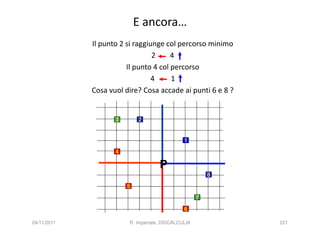
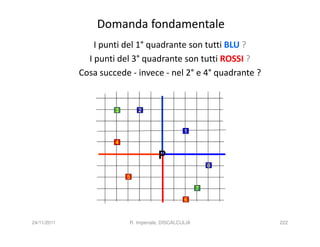
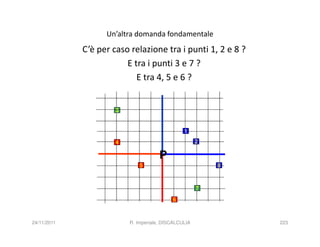
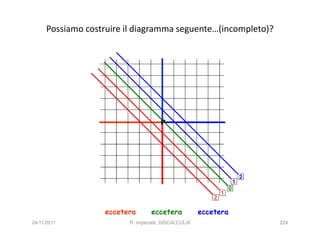
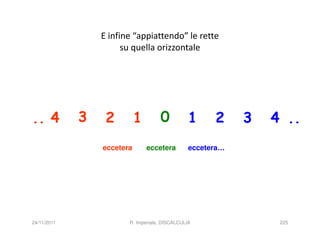
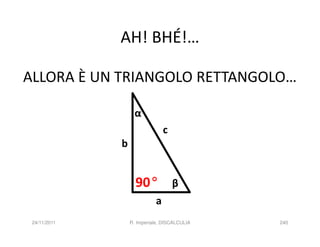
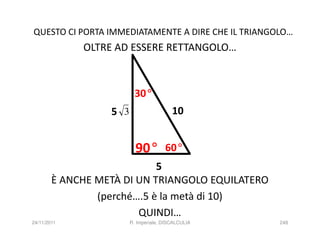
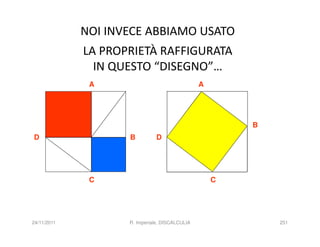
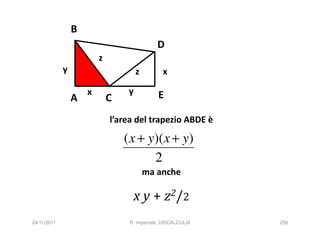
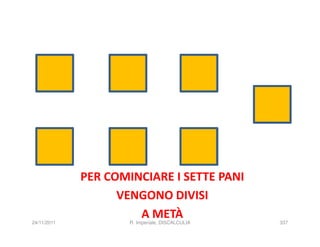
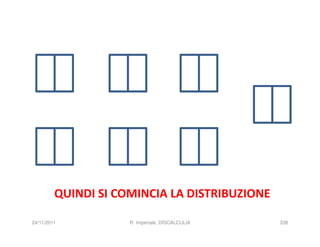
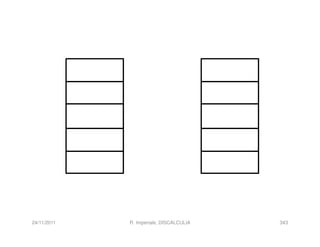
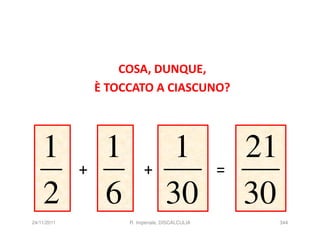
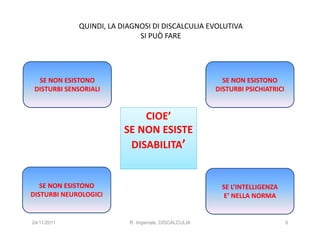
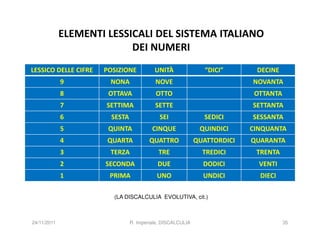
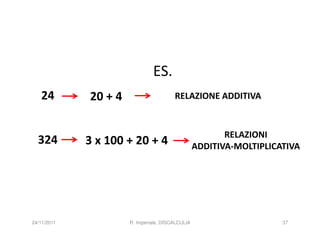
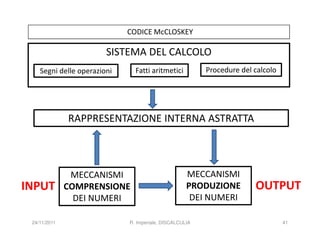
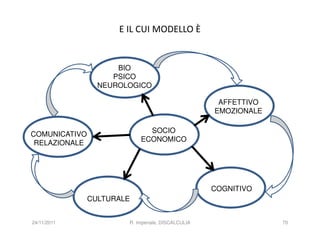
LA DISCALCULIA
È
“UN DISTURBO DELLE ABILITÀ
NUMERICHE E ARITMETICHE
CHE SI MANIFESTA IN BAMBINI
DI INTELLIGENZA NORMALE,
CHE NON HANNO SUBÌTO DANNI NEUROLOGICI.
ESSA PUÒ PRESENTARSI ASSOCIATA A DISLESSIA,
MA È POSSIBILE CHE NE SIA DISSOCIATA”
(LA DISCALCULIA EVOLUTIVA, cit.)


LA DISCALCULIA

È QUASI SEMPRE
ASSOCIATA IN CO-MORBILITÀ
ALLA DISLESSIA
ESSENDO MOLTO RARI
I CASI FINORA NOTI
DI DIASCALCULIA PURA

QUINDI, LA DIAGNOSI DI DISCALCULIA EVOLUTIVA
SI PUÒ FARE

SE NON ESISTONO SE NON ESISTONO
DISTURBI SENSORIALI DISTURBI PSICHIATRICI

CIOE’
SE NON ESISTE
DISABILITA’

SE NON ESISTONO SE L’INTELLIGENZA
DISTURBI NEUROLOGICI E’ NELLA NORMA


SECONDO L’ ICD 10 E IN ACCORDO CON QUANTO DESCRITTO NEL DSM-IV
I SINTOMI DELLE DIFFICOLTÀ ARITMETICHE SAREBBERO LE SEGUENTI
QUANTUNQUE L’ELENCO CONTENGA AFFERMAZIONI
DUBBIE E/O EQUIVOCHE

•INCAPACITÀ DI COMPRENDERE I CONCETTI DI PARTICOLARI OPERAZIONI
•MANCANZA DI COMPRENSIONE DI TERMINI O DI SEGNI ARITMETICI
•MANCATO RICONOSCIMENTO DEI SIMBOLI NUMERICI
•DIFFICOLTÀ AD ATTUARE LE MANIPOLAZIONI ARITMETICHE STANDARD
•DIFFICOLTÀ NEL COMPRENDERE QUALI NUMERI SONO PERTINENTI
AL PROBLEMA ARITMETICO CHE SI STA CONSIDERANDO
•DIFFICOLTÀ AD ALLINEARE CORRETTAMENTE I NUMERI
•DIFFICOLTÀ AD INSERIRE DECIMALI O SIMBOLI DURANTE I CALCOLI
•SCORRETTA ORGANIZZAZIONE SPAZIALE DEI CALCOLI
•INCAPACITÀ AD APPRENDERE LE TABELLINE DELLA MOLTIPLICAZIONE


BISOGNA – INVECE - AVERE CONSAPEVOLEZZA CHE LA DISCACULIA
VADA INQUADRATA E STUDIATA

IN UN QUADRO DI RIFERIMENTO NEUROBIOLOGICO
E NELLA SUA DIMENSIONE EVOLUTIVA
CIOÈ
NON COME PERDITA DI FUNZIONE
PRECEDENTEMENTE ACQUISITA
MA COME
DIFFICOLTÀ AD APPRENDERE E/O AUTOMATIZZARE
ALCUNI COMPITI NUMERICI E ARITMETICI

TUTTO CIÒ IMPLICA MOLTE COSE TRA CUI
IL DISCORSO
SULLE
MISURE COMPENSATIVE
E SULLE MISURE DISPENSATIVE

ESAMINIAMO BREVEMENTE SOLO IL CASO DELLA
«CALCOLATRICE»
E L’ASSOCIATO PROBLEMA
DELL’ORDINE DI GRANDEZZA DEI NUMERI


LA CALCOLATRICE

DEVE OBBLIGATORIAMENTE ESSERE USATA
DOPO AVER IMPARATO AD USARLA
PROBLEMI SCIENTIFICI E DIDATTICI COLLEGATI
1. ORDINE DI GRANDEZZA DEI NUMERI
2. CONFRONTO TRA NUMERI
3. L’ERRORE NELL’APPROSSIMAZIONE
4. I «NUMERI TROPPO GRANDI O TROPPO PICCOLI»
5. HO «DIGITATO BENE»?


L’EZIOLOGIA DEI DISTURBI EVOLUTIVI SPECIFICI
NON È NOTA

MA SI SUPPONE CHE VI SIA
L’INTERVENTO SIGNIFICATIVO
DI FATTORI BIOLOGICI
CHE INTERAGISCONO
SIGNIFICATIVAMENTE
CON FATTORI NON BIOLOGICI

CREDO SIA POSSIBILE IPOTIZZARE
CHE LA CAUSA SIA MULTIFATTORIALE E SIA DA RICERCARE
NELL’INTRECCIO AD INCIDENZA DIVERSIFICATA TRA
DISTURBI DEL LINGUAGGIO

DISTURBI DEL SISTEMA VISUO/PRASSICO

DISTURBI DEL SISTEMA UDITIVO

DISFUNZIONAMENTO DELLE MEMORIE DI LAVORO
E DELLA MEMORIA A LUNGO TERMINE

CAPACITÀ DI AUTOMATIZZAZIONE

DISTURBO DELLA RAPIDITÀ DI ELABORAZIONE
DELL’INFORMAZIONE

ELOGIO DELLA LENTEZZA

prof. di mat: «dai, sbrigati»

allievo disabile: «un momento, sto pensando»


ALCUNI AUTORI INDIVIDUANO LA CAUSE TRA

I DISTURBI LINGUISTICI (61%) COME DISORDINI DI TIPO

METAFONOLOGICO METALINGUISTICO
(46%) MISTO (28%)
(26%)
E I DISTURBI DEL SISTEMA VISUO/PRASSICO (11%)


DOVE LA METAFONOLOGIA

È L’ABILITÀ DI INDIVIDUARE
I SINGOLI SUONI DELLE PAROLE
ANCHE QUANDO SONO COARTICOLATI

È LA CAPACITÀ DI INTERVENIRE
SUI SINGOLI SUONI
PER COMPRENDERE, ANTICIPARE
O MODIFICARE LE PAROLE

OVVERO
1. RICONOSCIMENTO
DELLA STRUTTURA LINGUISTICA DELLA PAROLA

2. RICONOSCIMENTO DI RIME

3. CAPACITÀ DI SEGMENTARE (SILLABE-FONEMI)

4. CAPACITÀ DI FONDERE

5. RICONOSCIMENTO DI FONEMI

COSÌ CHE LA COMPETENZA METAFONOLOGICA
VIENE DEFINITA COME

UNA PARTICOLARE CONOSCENZA
METALINGUISTICA
CHE CONSISTE NELLA
CAPACITÀ DI PERCEPIRE E RICONOSCERE
PER VIA UDITIVA
I FONEMI CHE COMPONGONO LE PAROLE
DEL LINGUAGGIO PARLATO,
OPERANDO CON GLI STESSI ADEGUATE TRASFORMAZIONI
(UMBERTA BORTOLINI, 1995)


E LA COMPETENZA METALINGUISTICA

COME LA CAPACITÀ , PROPRIA DELL’ ESSERE UMANO
DI ELABORARE, FORMULARE, COMUNICARE
PENSIERI E VALUTAZIONI
CHE ABBIANO COME OGGETTO IL LINGUAGGIO IN GENERE,
LINGUE SPECIFICHE, LE VARIETÀ DI UNA LINGUA,
I SIGNIFICATI E LE FORME
DI UN TESTO, DI UNA FRASE, DI UNA PAROLA.
Berretta, Monica, “La competenza metalinguistica nella scuola di base”.
In: AA.VV, L’educazione linguistica dalla scuola di base al biennio della superiore ,
B. Mondadori, Milano 1984


PROBLEMI

DELL’AUTOREFERENZIALITÀ
DELL’AMBIGUITÀ SEMANTICA
DELL’INDECIDIBILITÀ…


TRE ESEMPI…

CHI CREDE
CHE GLI INSEGNANTI
DI QUESTA SCUOLA
NON SIANO BRAVI
DOVREBBE VEDERE
IL PRESIDE

PER TORNARE ALLA CAUSE, ALTRI AUTORI
RITENGONO CHE LE DIFFICOLTÀ SIANO PRODOTTE
DA UN SOLO FATTORE
(SINGLE FACTOR EXPLANATION)
cioè
• DISFUNZIONAMENTO DELLA MEMORIA DI LAVORO
o
• DISTURBO DELLA RAPIDITÀ DI ELABORAZIONE
DELL’INFORMAZIONE
o
• CAPACITÀ DI AUTOMATIZZAZIONE



NOI CREDIAMO, COMUNQUE
CHE QUESTO DERIVI DALL’INTRECCIO COMPLESSO DI CONCAUSE
ASCRIVIBILI - TRA LE ALTRE - ALLA

• GENETICA
• NEURODIVERSITÀ
COME CARATTERISTICA INDIVIDUALE

• ASIMMETRIA CEREBRALE

• FUNZIONE DEI NEURONI-SPECCHIO

ESSENDO LA “NEURODIVERSITÀ”

UN ATIPICO SVILUPPO NEUROLOGICO,
MANIFESTAZIONE DELLA UNICITÀ
E DELLA IRRIPETIBILITÀ
DELLO SVILUPPO INDIVIDUALE
E – IN DEFINITIVA –
DELL’IDENTITÀ INDIVIDUALE


CHE

PUÒ DETERMINARE
PARTICOLARI FUNZIONAMENTI CEREBRALI
COME AD ESEMPIO
QUELLO CHE ORGANIZZA E GOVERNA
LA COPPIA OPPOSITIVA QUASI-TEMPORALE
SINISTRA-DESTRA


E I NEURONI-SPECCHIO

“UN CIUFFO” DI NEURONI MOTORI
SCOPERTI ALL’INIZIO DEGLI ANNI NOVANTA
DEL SECOLO SCORSO
CH CONSENTONO AL NOSTRO CERVELLO
DI CORRELARE
I MOVIMENTI OSSERVATI A QUELLI PROPRI
E DI RICONOSCERNE “IL SIGNIFICATO”.
(G. RIZZOLATTI, C. SINIGAGLIA; SO QUEL CHE FAI, R.CORTINA EDITORE, MILANO, 2006


LA SCOPERTA DEI QUALI

CONSENTE DI ATTIVARE UN’INNOVATIVA INDAGINE
SULL’EVOLUZIONE DI INTELLIGENZA ED EMOZIONE,
DI PENSIERO E LINGUAGGIO.
UN’INDAGINE DESTINATA
A TRASFORMARE IL NOSTRO MODO DI CONCEPIRE
LE FUNZIONI DELLA MENTE
E A INFLUENZARE
PSICOLOGIA, ANTROPOLOGIA, ETICA ED ESTETICA.
“I NEURONI SPECCHIO SARANNO PER LA PSICOLOGIA
QUELLO CHE IL DNA È STATO PER LA BIOLOGIA”
(V.R. RAMACHANDRAN)


SOSTANZIALMENTE LA DISCALCULIA RIGUARDA

IL SISTEMA DI
IL SISTEMA DI
ELABORAZIONE E
E
PROCESSAZIONE CALCOLO
NUMERICA
(SISTEMA DEI NUMERI)

TRA CUI ESISTE “INDIPENDENZA FUNZIONALE”

IL SISTEMA DEI NUMERI SI STRUTTURA SU TRE LIVELLI
LIVELLO LESSICALE NOME DEI NUMERI

REGOLE DI GENERAZIONE
LIVELLO SINTATTICO DEI NUMERI
VALORE POSIZIONALE DELLE CIFRE

REGOLE DI COMPRENSIONE
LIVELLO SEMANTICO
DELLA QUANTITÀ


IL NOME DEI NUMERI

È RAPPRESENTABILE ATTRAVERSO I CODICI:

1. ALFABETICO ORALE (ES. LA PAROLA/NUMERO DETTA “SETTE”)

2. ALFABETICO SCRITTO (ES. LA PAROLA/NUMERO SCRITTA “SETTE”)

3. IL CODICE “ARABICO” (ES. L’IDEOGRAMMA “7”)

IL PASSAGGIO DA UN CODICE ALL’ALTRO SI CHIAMA

“TRANSCODIFICAZIONE NUMERICA”

PER ESEMPIO

•LA SCRITTURA SOTTO DETTATURA DEI NUMERI
•E LA LETTURA AD ALTA VOCE DEI NUMERI
IMPEGNANO LA “TRANSCODIFICAZIONE NUMERICA”

VEDIAMO ALCUNI ERRORI COMPIUTI DURANTE LA SCRITTURA
SOTTO DETTATURA DEI NUMERI

SCRIVI CENTOTRE: “1003”
SCRIVI MILLETRECENTOSEI: “10003006”
SCRIVI CENTOVENTIQUATTRO: “100204”
SCRIVI CENTOSETTE: “1007”

IL SISTEMA DEI

NUMERI
ASSEMBLA GLI ELEMENTI LESSICALI
(PRIMITIVI?)
IN ITALIANO
I NUMERI DALL’UNO AL NOVE
LE DECINE
I NUMERI DALL’UNDICI AL SEDICI
CUI AGGREGA GLI ELEMENTI “MISCELLANEI”
“CENTO” – “MILA” – “MILIONE” (…….)
CHE FUNGONO
DA
“MOLTIPLICATORI”


ELEMENTI LESSICALI DEL SISTEMA ITALIANO
DEI NUMERI
LESSICO DELLE CIFRE POSIZIONE UNITÀ “DICI” DECINE
9 NONA NOVE NOVANTA
8 OTTAVA OTTO OTTANTA
7 SETTIMA SETTE SETTANTA
6 SESTA SEI SEDICI SESSANTA
5 QUINTA CINQUE QUINDICI CINQUANTA
4 QUARTA QUATTRO QUATTORDICI QUARANTA
3 TERZA TRE TREDICI TRENTA
2 SECONDA DUE DODICI VENTI
1 PRIMA UNO UNDICI DIECI



LA COSTRUZIONE SINTATTICA DEI

NUMERI

PREVEDE
PER LA LINGUA ITALIANA
UNA COMPENENTE ADDITIVA
ED UNA MOLTIPLICATIVA
CHE SI POSSONO COMBINARE TRA LORO


ES.
24 20 + 4 RELAZIONE ADDITIVA

RELAZIONI
324 3 x 100 + 20 + 4 ADDITIVA-MOLTIPLICATIVA


LA COSTRUZIONE SINTATTICA DEI

NUMERI

PREVEDE
“LE REGOLE” DI SCRITTURA
DEI NUMERI
SECONDO
LA NOTAZIONE “POSIZIONALE”


IL SISTEMA DI
CALCOLO
RICEVE DAL
SISTEMA DEI NUMERI
L’INPUT - “IL NUMERO” -
LO ELABORA
“LO COMBINA”
E NE RESTITUISCE
L’OUTPUT - “IL RISULTATO” -


SECONDO ALCUNI AUTORI
(McCLOSKEY & al.)
L’USO DEI NUMERI
E
L’EFFETTUAZIONI DI CALCOLI
PRESUPPONE
LA LORO COMPRENSIONE
MEDIANTE “RAPPRESENTAZIONE INTERNA ASTRATTA”
MENTRE PER ALTRI
(CAMPBELL)
ESSA È POSSIBILE
MA NON OBBLIGATA


CODICE McCLOSKEY

SISTEMA DEL CALCOLO
Segni delle operazioni Fatti aritmetici Procedure del calcolo

RAPPRESENTAZIONE INTERNA ASTRATTA

MECCANISMI MECCANISMI
INPUT COMPRENSIONE PRODUZIONE OUTPUT
DEI NUMERI DEI NUMERI


“LA COMBINAZIONE”
FA SUPPORRE CHE IL SISTEMA
DI
CALCOLO
SIA ORGANIZZATO
SECONDO
TRE LIVELLI
(ATTIVATI DAL COMPITO)


CHE SONO
1. L’ELABORAZIONE DELE INFORMAZIONI NUMERICHE
CHE ATTRIBUISCE “SENSO” OPERATIVO
AI SEGNI DELLE OPERAZIONI (“+”, “x”, “<“, “=“..)
2. I COSIDDETTI “FATTI NUMERICI O ARITMETICI”
(LE OPERAZIONI DI BASE)
3. LE PROCEDURE DI CALCOLO
OVVERO IL RISPETTO DELLE REGOLE DI ESECUZIONE
DEGLI ALGORITMI
(ORDINE DELLE OPERAZIONI, INCOLONNAMENTO, RIPORTI, PRESTITI)


IN BREVE ED IN GENERALE,
LA “DISCALCULIA” EVOLUTIVA
SI DELINEA COME
DIFFICOLTÀ NEI COMPITI
NUMERICI ED ARITMETICI DI BASE
• CONTARE

• “GESTIRE” LA LINEA DEI NUMERI

• COMPRENDERE, LEGGERE, SCRIVERE E RIPETERE
I NUMERI

• EGUIRE CALCOLI A MENTE O PER ISCRITTO


PER QUEL CHE ABBIAMO DETTO, OCCORRE, DUNQUE

METTERE IN CAMPO
PROGETTI RIABILITATIVI
CHE TENGANO CONTO
DEI RISULTATI DELLA VALUTAZIONE

E DEI DATI QUOTIDIANI
DELLA DIA-GNOSIS
DELLA QUALE TRA POCO DIREMO


PERCHÉ
L’INTERVENTO RIABILITATIVO
– IN PARTICOLARE DELLE DIFFICOLTÀ -
PUÒ OTTENERE BUONI RISULTATI IN BREVE TEMPO

MENTRE LA RIABILITAZIONE DEL DISTURBO SPECIFICO
ASSUME UNA SPECIFICITÀ - PER TIPO E MODALITÀ -

DELLA QUALE OCCORRE PARLARE CON ASSOLUTA PUNTUALITÀ
E RICHIEDERNE L’IMPIEGO ISTITUZIONALE
CONTINUO E GRATUITO
PER TUTTI (BAMBINI, ADOLESCENTI, ADULTI…)


MA SOPRATTUTTO PERCHÉ
TRA QUELLE MODALITÀ
ED IL NOSTRO
“FAR MATEMATICA” PER LE DIFFICOLTÀ

ESISTONO DELLE INTERESSANTI INTERSEZIONI
DI CUI PARLAREMO

MA ...

PRIMA DI RIPRENDERE IL DISCORSO SULLA

DIA-GNOSIS
OCCORRE FARE ALCUNE PREMESSE


PER COMINCIARE CITIAMO UNA CATEGORIA “NOTA”
MA SPESSO DIMENTICATA…

24/11/2011
LA GRATUITÀ
R. Imperiale, DISCALCULIA 49

CHE È O DOVREBBE ESSERE

IL FILO ROSSO
COL QUALE
SI TENGONO TRA LORO
TUTTI I NOSTRI DISCORSI


IN PARTICOLARE…

LA GRATUITÀ
DEVE ESSERE
LA CONDIZIONE
DELLA VALUTAZIONE

COSA CHE, A MIO PARERE, DOVREBBE GENERARE
IL DIALOGO SEGUENTE…

1. IL MAESTRO AI RAGAZZI:
”IMPARATE E NON ASPETTATEVI ALCUN COMPENSO”
(CHE NON SIA IL PIACERE DI AVER IMPARATO)

2. I RAGAZZI AL MAESTRO:
“INSEGNA E NON ASPETTARTI ALCUNA RESTITUZIONE”
(CHE NON SIA IL PIACERE DI AVER INSEGNATO)


PERCHÉ … VA CONTINUAMENTE RICORDATO CHE

“A SCUOLA SI VA
PER IMPARARE”
(Scuola di Barbiana, Lettera a una professoressa)


DEL QUALE – COME DELL’INSEGNARE – LA SEGUENTE CITAZIONE
È UNA SPLENDIDA METAFORA

Ho intravisto l'angelo

nel blocco di marmo

e ho scolpito

fino a liberarlo.
Michelangelo

E CHE FAR SCUOLA
ABBIA UNA SOLA FINALITÀ…

LA VALORIZZAZIONE
DI CIASCUNO E DI TUTTI
ATTRAVERSO IL COMPIMENTO
DEL DIRITTO DI CITTADINANZA


AGITA

NEL SUO
“NATURALE” CONTESTO
LA RELAZIONE EDUCATIVA
RECIPROCA E ASIMMETRICA
NELLA QUALE L’INSEGNANTE
DEVE SAPER CREARE “BENESSERE”

LA RECIPROCITÀ DELLA RELAZIONE

IMPONE
CHE INSEGNANTE ED ALLIEVO
SI “CONOSCANO”
NEL PARLARSI/ASCOLTARSI


E L’ASIMMETRIA IMPONE:

CHE L’INSEGNANTE NON SIA
AMICO DEI SUOI RAGAZZI

CHE SIA AUTOREVOLE ED ESEMPLARE

CHE SAPPIA GESTIRE IL “PARADOSSO”
DELLA DISTANZA EDUCATIVA


DISTANZA CHE CONTEMPORANEAMENTE
DEVE ESSERE

LA MINORE
E LA MAGGIORE
POSSIBILE

AFFINCHÉ

EGLI SIA VICINISSIMO
AI SUOI RAGAZZI
QUANDO ESSI LO CHIAMINO,
MAGARI PER POTER “ERRARE”


PERCHÉ

“APPRENDERE
DÀ INIZIO ALL’ERRANZA”
(M. Serres, Il mantello di Arlecchino, Marsilio, Venezia, 1992)


E PER

“LASCIARSI
UN BEL GIORNO
SEDURRE”
(M. SERRES, cit.)

DA LUI
CHE DEVE ESSERE
CAPACE DI SEDURRE
(SECUM-DUCERE)


DELLE MODALITÀ
PER
“NEGOZIARNE I SIGNIFICATI”


MA

L’INSEGNANTE CHE VOGLIA
SEDURRE I SUOI RAGAZZI
DEVE NECESSARIAMENTE
DISPORRE DI MOLTE
“PAROLE PER DIRLO”

Modalità contenute nella seguente citazione
«Il metodo che consiste
nel proporre e riproporre
una negoziazione sui significati
con la mediazione
dell'interpretazione narrativa
costituisce a mio avviso
uno dei grandi risultati
dello sviluppo umano
in senso ontogenetico, culturale e filogenetico»
(J. BRUNER, LA RICERCA DEL SIGNIFICATO, BOLLATI BORINGHIERI, TORINO, 1992)

“PERCHÉ È SOLO LA LINGUA
CHE FA EGUALI”
INFATTI

“EGUALE È CHI SA ESPRIMERSI
E INTENDE L’ESPRESSIONE ALTRUI”
(Scuola di Barbiana, LETTERA A UNA PROFESSORESSA)


TUTTO CIÒ
AFFINCHÉ
L’IDENTITÀ INDIVIDUALE
DI CIASCUNO


CHE

E’ UN SISTEMA COMPLESSO DINAMICO
COSTITUITO DA SOTTOSISTEMI
CHE CHIAMO “PROFILI DI IDENTITA’”
CO-EVOLVENTI
TRA LORO IN RECIPROCA
RELAZIONE RETROATTIVA


E IL CUI MODELLO È

BIO
PSICO
NEUROLOGICO

AFFETTIVO
EMOZIONALE

SOCIO
COMUNICATIVO
ECONOMICO
RELAZIONALE

COGNITIVO
CULTURALE


EVOLVA POSITIVAMENTE
E CON ESSA
SI REALIZZI
IL “PROGETTO DI VITA”
DI CIASCUNO
I SUOI SOGNI ED I SUOI DESIDERI


TENDENDO INFINE VERSO
L’IDENTITÀ SOCIALE
CHE È – APPUNTO -
LA SUA CONTESTUALIZZAZIONE
NELLA CIVITAS
OVVERO NELLA
«TRAMA DI RELAZIONI»
CHE DEFINISCE CIASCUNO COME UOMO


PER QUESTO
ESSA È UNICA ED IRRIPETIBILE
E DETERMINA
L’ASSIOMA FONDAMENTALE
DELLA DIDATTICA E DELLA PEDAGOGIA:

OGNI RAGAZZO
È UNICO E IRRIPETIBILE

QUESTO
È IL MOTIVO PER IL QUALE
ANCHE LA DIA-GNOSIS
(DI CUI DIREMO TRA POCO)
È STRUMENTO PARZIALE
NON ADATTO AD ESPRIMERE GIUDIZI “CERTI”
E DEFINITIVI
O FARE “PREVISIONI”


QUESTO
È IL MOTIVO PER IL QUALE
NEMMENO LE SEDUCENTI
“PAROLE PER DIRLO”
BASTANO
SE NON SIANO CONTESTUALIZZATE


CIOÈ SE NON SI DIA
“CONOSCENZA NELLA RELAZIONE”
CHÈ
È PROPRIO
IL SIGNIFICATO NUCLEARE
DELLA PAROLA GRECA
DIA-GNOSIS

INFATTI
“DIAGNOSI”
Deriva dal greco διάγηωσις
(DIA-GNOSIS/DIA-GIGNOSKEIN)
composto di
dia “attraverso” e gnosis “conoscenza”
e vuole – appunto - dire
“CONOSCENZA ATTRAVERSO”
cioè
CONOSCENZA RELAZIONALE

SI ATTIVA “STRADA FACENDO”…

La diagnosi è procedura complessa e dinamica;
È INTERMINABILE e si attiva
“STRADA FACENDO”
e
“GIORNO DOPO GIORNO”


STRADA FACENDO...

Camminante, son le tue orme
il cammino e nulla più;
camminante, non c’è cammino
il cammino si fa nell’andare.
EL CAMINANTE
ANTONIO MACHADO


SE DUNQUE
SI VUOL “FAR SCUOLA”
È INELUDIBILE
IL CONOSCERSI IN RELAZIONE
CHE È IL MOMENTO CENTRALE
OLTRE CHE
LA PREMESSA NECESSARIA
DELL’IMPARARE
E DELL’INSEGNARE


IN DEFINITIVA, IL FAR SCUOLA
È L’ INTRECCIO COMPLESSO TRA

1. LA DIA-GNOSIS/CONOSCENZA

2. L’INSEGNARE

3. L’IMPARARE (COMPRENDERE + APPRENDERE)

4. LA DIA-GNOSIS/VALUTAZIONE


MODELLIZZATO COME SEGUE

DIA-GNOSIS/CONOSCENZA
INSEGNARE IMPARARE
DIA-GNOSIS/VALUTAZIONE


DATO CHE INSEGNARE

È

“ENTRARE NEI SEGNI DI…”


E IMPARARE È

“COMPRENDERE”
+
“APPRENDERE”


INFATTI

“COMPRENDERE” (CUM-PRENDERE)
È
“PRENDERE QUALCOSA INSIEME CON”

“APPRENDERE” (AD-PRENDERE)
È
“ INSERIRE QUELLA COSA NEI PROPRI APPARATI”
(COGNITIVI, AFFETTIVI, MNESTICI)


QUESTO DICE CHE QUANDO
CON ALTRI
SI SIANO SVELATI I SIGNIFICATI DELLE PAROLE
FACENDO DEL COMPRENDERE
UN ATTO SOCIALE
E SI SIANO INSERITI QUEI SIGNIFICATI
NEI NOSTRI SAPERI
FACENDO DELL’APPRENDERE
UN ATTO INDIVIDUALE
ALLORA ABBIAMO IMPARATO


TUTTAVIA L’IMPARARE
INTESO COME COMPRENSIONE + APPRENDIMENTO
NON È ANCORA COMPLETATO.
LEGGETE LA SEGUENTE DICHIARAZIONE,
FATTA DA UN RAGAZZO 15ENNE ALLA SUA INSEGNANTE

QUANDO IMPARO QUALCOSA
SENTO CHE QUELLA COSA NON MI APPARTIENE
FINO A QUANDO NON NE HO PARLATO
CON QUALCUNO.
SOLO ALLORA QUEL SAPERE
DIVENTA MIO PER SEMPRE.


QUINDI, CONCLUDENDO

IL PROCESSO
INSEGNARE/IMPARARE
SI SVOLGE
IN TRE MOMENTI:

SOCIALE INDIVIDUALE SOCIALE


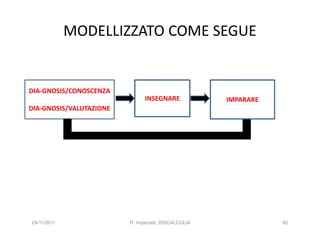
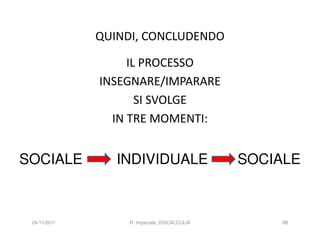
MOMENTI CHE CONNETTONO IL SOCIALE E L’INDIVIDUALE
DI OGNUNO CON UN LEGAME NECESSARIO FINALMENTE
CERTIFICATO (ANCHE) DALLE NEUROSCIENZE
“Il sistema dei neuroni specchio appare così decisivo per
l’insorgere di quell’esperienza comune che è all’origine
della nostra capacità di agire come soggetti non soltanto
individuali ma anche e soprattutto sociali […]. Non solo: la
nostra stessa possibilità di cogliere le reazioni emotive
degli altri è correlata a un determinato insieme di aree […]
specchio. Al pari delle azioni, anche le emozioni risultano
immediatamente condivise […]. Ciò mostra quanto
radicato e profondo sia il legame che ci unisce agli altri,
ovvero quanto bizzarro sia concepire un io senza un noi”
(G. Rizzolatti & C. Sinigaglia, So quel che fai, Raffaello Cortina Editore, Milano 2006)


IN DEFINITIVA

L’INTRECCIO DINAMICO, NON DETERMINISTICO,
CAOTICO, IMPREVISTO, NON PROGRAMMATO,
NON PROGNOSTICO
CHE ISTANTE PER ISTANTE SI CELEBRA
TRA LE “PAROLE” DI OGNI RAGAZZO
E LE “PAROLE” DELL’INSEGNANTE
GRAZIE ANCHE AL MODO
TOTALMENTE CORPOREO E MATERIALE
DELLA RELAZIONE INSTAURATA
E CHE CHIAMIAMO “DIA-GNOSIS”
STABILISCE L’UNIONE-DISTANZA
TRA L’INSEGNARE E L’IMPARARE

CERTO: TROVARE «LE PAROLE PER DIRLO»
COME È FACILE INTUIRE
FA DEL LINGUAGGIO
IL CENTRO DI TUTTO IL NOSTRO DISCORSO
SEBBENE ESSO SIA IL «COLPEVOLE»
MA CONTEMPORANEMENTE
E FORTUNATAMENTE
ANCHE IL «MEDICO»
DI OGNI DISTURBO E DI OGNI DIFFICOLTÀ

DEL RESTO…

IL “PENSIERO MATEMATICO”
ALTRO NON È SE NON
“UN MODO SPECIALIZZATO DI USARE
LA NOSTRA PREDISPOSIZIONE
PER IL LINGUAGGIO”
(K. Devlin, Il gene della matematica, Longanesi, Milano, 2002)


INFATTI, È OVVIO INTUIRE CHE

IL LINGUAGGIO
CONTIENGA E PRESENTI
ALCUNI NODI
CHE VANNO SCIOLTI…
CON IL LINGUAGGIO!

UNO DEI NODI DEL LINGUAGGIO

RIGUARDA

L’INTERPRETAZIONE
DELLE PAROLE, DELLE FRASI, DEI TESTI…


SI CONSIDERI COME CELEBRE ESEMPIO
«LA FRASE» SEGUENTE

(a + b) 2 = a 2+ 2ab+ b 2

IN GENERE ESSA VIENE «VENDUTA»

COME

IL QUADRATO DEL BINOMIO

FERMO RESTANDO IL FATTO
CHE PAROLE COME

«MONOMIO», BINOMIO» ECC..

VANNO, APPUNTO, NEGOZIATE

ED INTERPRETATE…

LA NOSTRA «FRASE»

(a + b) 2 = a 2+ 2ab+ b 2

COM’È NOTO, RAPPRESENTA

IL QUADRATO DEL BINOMIO

SE E SOLO SE a, b SONO «NUMERI»


Se fossero segmenti accadrebbe ciò che segue…
Dato un quadrato, con quattro punti A, B, C e D dividiamone ogni lato
in due parti lunghe rispettivamente “a” e “b”;
quindi congiungiamo A con C e B con D.
A
a b

a

D B

b
C

DUNQUE, L’AREA DEL NOSTRO QUADRATO
RISULTA ESSERE LA SOMMA DI…

a2 ab

ab b2
CIOÈ:
a 2+ 2ab+ b 2

E LA NOSTRA «FRASE»

(a + b) 2 = a 2+ 2ab+ b 2

ORA SI LEGGE:

«L’AREA DEL QUADRATO DI LATO a +b

È UGUALE A….»


MA NON È FINITA…LA «FRASE»

(a + b) 2 = a 2+ 2ab+ b 2
FATTE LE DEBITE PROPORZIONI
POTREBBE ESSERE «RAPPRESENTATA» COSÌ COME SEGUE:

a b

a b a b

a2 ab ba b2

CON UNA TECNICA CHE RITROVEREMO ANCORA

CONSENTENDOCI DI LEGGERE «MOLTE COSE»
AD ESEMPIO
SE a, b FOSSERO RISPETTVAMENTE «PAPÀ» E «MAMMA»
A PARTIRE DA

ME
a b

a b a b

a2 ab ba b2
OTTERREI: IL PAPÀ DI PAPÀ, IL PAPÀ DI MAMMA,
LA MAMMA DI PAPÀ, LA MAMMA DI MAMMA
CIOÈ IL «NOME» DEI MIEI QUATTRO NONNI

E SE
a, b FOSSERO RISPETTVAMENTE «TESTA» E «CROCE» ?
LA MIA «FRASE» SAREBBE LO SPAZIO-EVENTI
DEL LANCIO CONTEMPORANEO DI DUE MONETE, CIOÉ

a b

a b a b

a2 ab ba b2
2 TESTE, 1TESTA-CROCE, 1 CROCE-TESTA, 2 CROCI
OVVERO, I FAMOSI «QUATTRO CASI POSSIBILI»


E SE
a, b FOSSERO RISPETTVAMENTE «ACCESO» E «SPENTO» ?
E SE…? E SE…?
COME S’È VISTO, LA NOSTRA «FRASE»
- SINTATTICAMENTE CORRETTA–
CHOMSKY DIREBBE
«A STRUTTURA SUPERFICIALE INVARIANTE »
PRESENTA NUMEROSE «INTERPRETAZIONI»
CHE VARIANO A SECONDA DEI NOMI
CHE SI DÀNNO AD a, b
IN DEFINITIVA ESSA È UNA POLISEMIA
«QUASI» SIMILE ALLA CELEBRE
«UNA VECCHIA PORTA LA SBARRA»

DUNQUE, FINALMENTE…

PARLIAMO DELLA DIA-GNOSIS

CHE OLTRE A

«CONOSCENZA IN RELAZIONE»


VALE ANCHE

“VALUTAZIONE”
(Cortellazzo & Zolli, DIZIONARIO ETIMOLOGICO)


DUNQUE SI PUÒ AFFERMARE CHE

DIAGNOSI CONOSCENZA
E
DIAGNOSI VALUTAZIONE
SIANO
PER TRANSITIVITÀ SINONIMICA
“LA STESSA COSA”

LA DIAGNOSI/CONOSCENZA
DI FATTO CONSISTE
NELL’ANALISI RELAZIONALE
E QUALITATIVA
DELL’IDENTITA’
INDIVIDUALE E SOCIALE
DI OGNI RAGAZZO

MENTRE…

LA DIAGNOSI/VALUTAZIONE
DI FATTO CONSISTE
NELL’ANALISI RELAZIONALE
E QUALITATIVA
DELLE MODIFICAZIONI
DELL’IDENTITA’ STESSA

DUNQUE, CHI VOGLIA CONOSCERE “GIORNO DOPO GIORNO”
OGNI SUO RAGAZZO DEVE CHIEDERE E CHIEDERSI

1. CIÒ CHE SA
2. CIÒ CHE SA DI SAPERE/CIÒ CHE SA DI NON SAPERE
3. CIÒ CHE NON SA
4. CIÒ CHE NON SA DI SAPERE/CIÒ CHE NON SA DI NON SAPERE
5. CIÒ CHE SA FARE/CHE NON SA FARE
6. CIÒ CHE DESIDERA
7. CIÒ CHE GLI PIACE/CHE NON GLI PIACE
8. CIÒ CHE GLI PIACEREBBE FARE ADESSO
9. CIÒ CHE GLI PIACEREBBE FARE DA GRANDE


E

1. COME PARLA

2. QUANTE PAROLE CONOSCE

3. COME COMUNICA

4. COME SI RELAZIONA

E QUALI SIANO LE MODALITÀ D’IMPIEGO
DELLE FUNZIONI SUPERIORI

1. IL PENSIERO
CONVERGENTE-DIVERGENTE-RIFLESSIVO
O PIÙ PRECISAMENTE
AUTODIAGNOSTICO/METACOGNITIVO

2.LA MEMORIA
(RECENTE-CRITICA/PROFONDA)

QUINDI VERIFICARE

LA PRESENZA
DI ALCUNE FONDAMENTALI
CAPACITÀ/ABILITÀ
(CHE “SI USANO ANCHE IN MATEMATICA”)
MA CHE DEFINIAMO TRASVERSALI
CHE TROVANO IL NUCLEO
DEL LORO CONSISTERE…
NEL LINGUAGGIO…

TUTTO CIÒ CONTRASTA
CON QUEL CHE REALMENTE
AVVIENE
NELLE NOSTRE SCUOLE
VEDIAMOLO
ATTRAVERSO UNA BREVE ANALISI
DELLE «CONSUETE»
PROCEDURE DI VALUTAZIONE

SPESSISSIMO ACCADE CHE

ALLA VALUTAZIONE SI DIANO
SIGNIFICATI TEORICI E PROCEDURALI
ASSAI DIVERSI
a. VALUTAZIONE COME INDAGINE SUI PROCESSI
vs
b. VALUTAZIONE COME MISURAZIONE DEI
PRODOTTI

CHE NON SI CONOSCANO
NÉ TEORIE
NÉ IPOTESI EPISTEMOLOGICHE
O ALMENO QUALCHE MODALITÀ PROCEDURALE
CONDIVISA E AFFIDABILE
NEL TEMPO
CHE NON FACCIA CAMBIARE
“PARERE”, GIUDIZIO”
O
“VALUTAZIONE


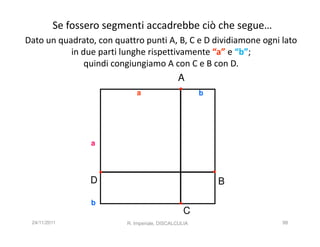
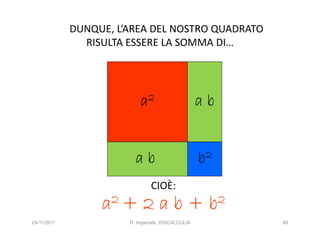
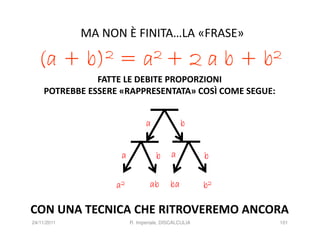
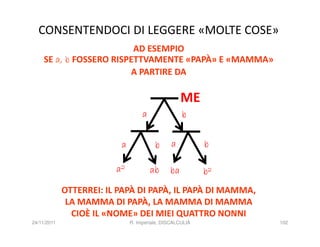
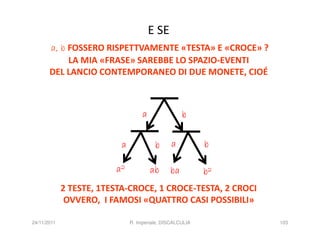
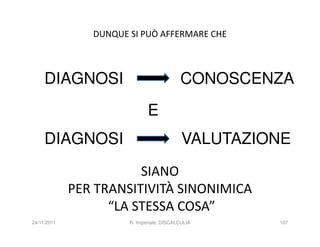
INFATTI, ALCUNE RICERCHE
SULL’AFFIDABILITÀ DEI VOTI ASSEGNATI
DIMOSTRANO

“[..] NON SOLO CHE LO STESSO COMPITO
(SAGGIO, PROVA SCRITTA DI VARIE MATERIE)
VIENE VALUTATO DIVERSAMENTE
DA DIVERSI INSEGNANTI,
MA CHE VIENE VALUTATO DIVERSAMENTE
PERFINO DALLO STESSO INSEGNANTE
IN UN DIVERSO MOMENTO”.
(M. LICHTNER)


CHE ALCUNI PENSINO CHE
I LORO STRUMENTI DI VALUTAZIONE
SIANO
“CERTAMENTE OGGETTIVI”
DIMENTICANDO CHE QUANDO SI “CONFRONTANO”
LE SEMANTICHE DI CHI “PREPARA” LE PROVE
AMMESSO CHE ESSE SIANO LEGITTIME
CON QUELLE DEL RAGAZZO CHE DEVE
“SUBIRLE”
SI GENERA SCARTO DI SIGNIFICATI
CHE RENDE SOGGETTIVE
RISPOSTA E VALUTAZIONE.


E NON QUELLA DELLA «FAMOSA»
INSUFFICIENZA NEL COMPITO DI GEOMETRIA
OVVERO:

I SOLIDI IGNOTI
Dalla Settimana Enigmistica (n° 4152 del 22/10/2011):


A PROPOSITO DI PROVE LEGITTIME VON FOERSTER SCRIVE :
«DEFINIRÒ 'DOMANDA ILLEGITTIMA'
QUELLA DOMANDA DI CUI SI CONOSCA GIÀ LA RISPOSTA.
NON SAREBBE AFFASCINANTE IMMAGINARE
UN SISTEMA DI ISTRUZIONE
CHE CHIEDA AGLI STUDENTI DI RISPONDERE SOLO
A 'DOMANDE LEGITTIME',
CIOÈ A DOMANDE LE CUI RISPOSTE SIANO IGNOTE?
NON SAREBBE ANCORA PIÙ AFFASCINANTE IMMAGINARE UNA SOCIETÀ
DISPOSTA A CREARE UN SIMILE SISTEMA DI ISTRUZIONE?
LA CONDIZIONE NECESSARIA DI QUESTA UTOPIA SAREBBE
CHE I MEMBRI DI UNA SIMILE SOCIETÀ SI PERCEPISSERO RECIPROCAMENTE
COME ESSERI AUTONOMI, NON-BANALI.
SE UNA SOCIETÀ DEL GENERE ESISTESSE,
SONO CERTO CHE VI SI FAREBBERO LE PIÙ STRAORDINARIE SCOPERTE».
[Heinz von Foerster, Sistemi che osservano, Astrolabio, Roma, 1987, pag. 130]

L’UNICA FORMA PRATICATA
DI VALUTAZIONE
SIA LA COSIDDETTA
“VALUTAZIONE SOMMATIVA”
CHE È TEORICAMENTE POSSIBILE


INFATTI
“FARE LA MEDIA” TRA NUMERI/VOTI
(FORSE) SI PUÒ.
“FARE LA MEDIA”
TRA
“AGGETTIVI QUALIFICATIVI”
E LORO IMMAGINIFICHE ALTERAZIONI
NON SI POTREBBE.


MA ILLECITA
PERCHÉ CONSISTE
NEL METTERE INSIEME
“FONDENDOLI”
RISULTATI DIVERSI
OTTENUTI IN TEMPI DIVERSI


SAREBBE COME PRENDERE
LE VARIE IDENTITÀ DEI RAGAZZI
E MESCOLARLE PER DAR LUOGO
AL COSIDDETTO
“ALLIEVO MEDIO”
NOTORIAMENTE INESISTENTE
MA SUL QUALE SI SONO COSTRUITI – APPUNTO -
I CONCETTI DI
PROGRAMMA
E DI
VALUTAZIONE


LE STESSE INDICAZIONI NAZIONALI DEL 2007
FANNO A QUESTO PROPOSITO
UN’AFFERMAZIONE NETTA:
“Le trasmissioni standardizzate e normative
delle conoscenze
che comunicano CONTENUTI INVARIANTI
pensati per
INDIVIDUI MEDI
non sono più adeguate”


QUESTA SAREBBE STATA
ANCORA PIÙ NETTA
E TOTALMENTE CONDIVISIBILE SE AVESSE DICHIARATO:
“Le trasmissioni standardizzate e normative
delle conoscenze
che comunicano
PAROLE INVARIANTI
PENSATE per
INDIVIDUI MEDI
non sono più adeguate”

DA QUESTO
POSSIAMO FAR DISCENDERE
ALCUNE CONSIDERAZIONI
SULL’INDIVIDUALIZZAZIONE
E
SULLA PERSONALIZZAZIONE
DELLA DIDATTICA

IN BREVE, PER QUEL CHE MI RIGUARDA
L’INDIVIDUALIZZAZIONE
È L’IMPIEGO CONSAPEVOLE
DI METODOLOGIE E DI «PAROLE»
ADATTE ALL’IDENTITÀ INDIVIDUALE
LA PERSONALIZZAZIONE
È LA SCELTA DI CONTENUTI DISCIPLINARI
RITENUTI CONFACENTI
A QUELL’IDENTITÀ
(Vedi legge 170/2010 e linee guida)

MESCOLANDO
“CAOTICAMENTE”
TUTTO QUANTO ABBIAMO DETTO
CONCLUDIAMO CHE
LA
“VALUTAZIONE OGGETTIVA”
È IMPOSSIBILE
PER CARENZA ONTOLOGICA
ED EPISTEMOLOGICA


ANCHE PERCHÉ…

“È SINTATTICAMENTE E SEMANTICAMENTE CORRETTO DIRE
CHE LE ASSERZIONI SOGGETTIVE
SONO FATTE DA SOGGETTI.
ALLORA, IN MODO CORRISPONDENTE,
POTREMMO DIRE CHE LE ASSERZIONI OGGETTIVE
SONO FATTE DA OGGETTI.
DISGRAZIATAMENTE
QUESTE DANNATE COSE NON FANNO ASSERZIONI”

(H. VON FOERSTER, cit.)

E ALLORA

ADDIO AL FANTASMA
DELLA VALUTAZIONE “OGGETTIVA”
AI DEBITI, AI CREDITI
ALLA MERCIFICAZIONE DEL SAPERE
CHE INVECE “DEVE” ESSERE
“DISINTERESSATO”
E ADDIRITTURA «IN-UTILE»


E (poiché) DIO DISSE:
“SIANO LE COMPETENZE” E LE COMPETENZE
INVASERO LE MENTI E I CUORI DI TUTTI GLI
UOMINI. NON SI TROVÒ COSÌ PIÙ NULLA CHE
NON AVESSE UNA COMPETENZA. ANCHE IL
RIPOSO, E DIO SI CHIESE SE IL SUO RIPOSO
FOSSE UNA COMPETENZA, SE LUI IN REALTÀ
“SAPESSE RIPOSARE”. COSÌ SUBENTRÒ UN
TERRIBILE DUBBIO.
(LUCIO GUASTI, Competenze e formazione; in: ScuolaInsieme, n° 5/2006)


ADDIO ALLE COMPETENZE
QUANDO NON SIANO
L’INDICE DELLA TRASFORMAZIONE
DELLE CAPACITÀ IN ABILITÀ
OVVERO DEI
SAPERI/ISTRUZIONE
IN
SAPERI/IDENTITÀ


NON È UNA COMPETENZA
“SAPERE” IL TEOREMA DI PITAGORA
MENTRE
APPROSSIMA LA COMPETENZA
“SCOPRIRE”
SE L’ANGOLO FORMATO DA DUE SPIGOLI
SIA O NO RETTO
DISPONENDO SOLO
DI QUALCHE CORDICELLA
E DI UN RIGHELLO

COME SI FA?


DI CHE “COSA CI SIAMO SERVITI”?

PROCEDURA 90°

30 cm


PERCIÒ RI-PROPONGO

CHE LA VALUTAZIONE
PERDA IL SUO CARATTERE DI
OPERAZIONE EXTRADIDATTICA
E SI CON-FONDA NEL
“FAR SCUOLA”
PER DIVENTARNE
“IL MOMENTO FONDAMENTALE”


PERCHÉ ANCH’IO HO SOGNATO

“DI POTER UN GIORNO FONDARE UNA
SCUOLA IN CUI SI POTESSE APPRENDERE
SENZA ANNOIARSI, E SI FOSSE STIMOLATI A
PORRE PROBLEMI E A DISCUTERLI; UNA
SCUOLA IN CUI NON SI DOVESSERO SENTIRE
RISPOSTE NON SOLLECITATE A DOMANDE
NON POSTE; IN CUI NON SI DOVESSE
STUDIARE AL FINE DI SUPERARE GLI ESAMI.”
(K.L. POPPER)


MA NON C’È DUBBIO CHE

ESSA DEBBA ESSERE
LA DECLINAZIONE
DELLO SCARTO
TRA IL PROGETTATO
ED IL REALIZZATO


PERCHÉ

QUELLO SCARTO
È
L’ERRANZA


E

«L’ERRARE»
DECLINA
LA GRANDE SCOMMESSA,
LA SEGUENTE:

NELL’ERRARE
OGNI RAGAZZO
VUOL ESSERE GUIDATO MA
“SENZA INTERFERENZE”

CIOÈ

SENZA CHE SI ESERCITI
IL “POTERE PEDAGOGICO”
DEI GIUDIZI
E DELLE PREVISIONI

INFATTI

LA RICERCA VERA
È
L’ANDARE SENZA SAPERE DOVE
MA MUOVENDOSI CON ALTRI
CIOÈ
CUM-MOVENDOSI


TUTTO CIÒ…PREMESSO
POSSIAMO FINALMENTE PARLARE
DELL’IMPARARE/INSEGNARE MATEMATICA
ALLE PERSONE DISABILI
ALLE PERSONE CON DSA
ALLE PERSONE CON DIFFICOLTÀ
ALLE PERSONE CON DISAGIO

ALLE PERSONE

DICENDO SUBITO CHE

UNA DELLE CAUSE CHE IMPEDISCE L’IMPARARE
STA NELLE INTERFERENZE
DELLE EMOZIONI E DELL’AFFETTIVITÀ
SUL PROFILO COGNITIVO.
LA PIÙ CONOSCIUTA È LA FAMOSA
“PAURA DELLA MATEMATICA”
(v. R. Imperiale, Chi ha paura della matematica? Io…o forse no; in: Matematica e Difficoltà;
Atti del Convegno Nazionale n°7, Pitagora Editrice, Bologna, 1998)


E CHE…

La parola MATEMATICA
deriva dal greco
μάθημα (máthema),
traducibile con i termini
"scienza", "conoscenza" o "apprendimento“
μαθηματικός (mathematikós)
significa dunque
"incline ad apprendere"

LA QUALE, COME AVEVAMO ANTICIPATO

SI “COSTRUISCE”
GRAZIE ALL’USO DI ALCUNE
CAPACITÀ/ABILITÀ
CHE DICIAMO TRASVERSALI:


CHE, NON ESAUSTIVAMENTE, SONO

1. SAPERSI ORIENTARE NELLO SPAZIO/TEMPO
2. SAPER METTERE IN RELAZIONE
(analogica, causale, implicativa…)
3. SAPER CLASSIFICARE E ORDINARE
4. SAPER COMBINARE OGGETTI
5. SAPER RISOLVERE PROBLEMI


E CHE RIASSUMONO IL PENSIERO DI K. DEVLIN.
SECONDO LUI, INFATTI, PER FARE MATEMATICA OCCORRONO:

1. IL SENSO DEL NUMERO
2. LA CAPACITA’ NUMERICA
3. LA CAPACITA’ ALGORITMICA
4. LA CAPACITA’ DI DESTREGGIARSI CON L’ASTRAZIONE
5. UNA PERCEZIONE DELLA CAUSA E DELL’EFFETTO
6. LA CAPACITA’ DI COSTRUIRE E SEGUIRE
UNA CONCATENAZIONE CAUSALE DI EVENTI
7. LA CAPACITA’ DI RAGIONAMENTO LOGICO
8. LA CAPACITA’ DI RAGIONARE IN TERMINI DI RELAZIONI
9. LA CAPACITA’ DI RAGIONAMENTO SPAZIALE
(K. DEVLIN, IL GENE DELLA MATEMATICA, cit.)

SERVE A QUALCOSA
INSEGNARE E IMPARARE MATEMATICA? SERVE

ALLA CONQUISTA DELL’AUTONOMIA:
1. DI GIUDIZIO

2. DI PRASSI

3. DI COMUNICAZIONE/RELAZIONE


Matematica: Perché? Cosa?
La matematica ha uno specifico ruolo La competenza matematica
nello sviluppo della capacità generale
è la capacità di un individuo
di operare
di
e comunicare significati […]
per rappresentare identificare e comprendere il ruolo
e che la matematica
costruire modelli di relazioni gioca nel mondo reale,
fra oggetti ed eventi. di operare valutazioni fondate
In particolare, la matematica dà strumenti per e di utilizzare la matematica
la descrizione scientifica del mondo
e confrontarsi con essa
e per affrontare
in modi che rispondono
problemi utili nella vita quotidiana;
inoltre contribuisce a sviluppare
alle esigenze della vita
la capacità di comunicare e discutere, di quell’individuo in quanto cittadino
di argomentare in modo corretto, che esercita un ruolo costruttivo,
di comprendere impegnato e basato sulla riflessione.
i punti di vista e le argomentazioni degli altri. (OCSE-PISA 2003)
(Indicazioni Nazionali 2007)


DUNQUE

“SERVE” A VALORIZZARE
LA DIVERSITÀ DI CIASCUNO
(E DI TUTTI)
IN UN QUADRO DI
“UGUAGLIANZE SOSTANZIALI”
E PERCIÒ
A GARANTIRE IL DIRITTO
ALLA “CITTADINANZA”

MA

DI CIÒ
SI DIRÀ POI…


PER PIACERE,

VORREI CONTARE…


PRIMA DI PROCEDERE BISOGNA TENER CONTO CHE
“L’ACCESSO ALLA QUANTITÀ”
È ADDIRITTURA PRE-VERBALE
E – ALCUNI (NON IO!) PENSANO – INNATO
E CHE ESSO PRESIEDE ALL’APPRENDIMENTO
DELLA LETTURA E SCRITTURA DEI NUMERI
E AI SISTEMI DI CONTEGGIO,
DA CUI POSSONO AVERE ORIGINE
I MECCANISMI DI CALCOLO E DI MANIPOLAZIONE
DEL SISTEMA NUMERICO
DI CUI ABBIAMO DETTO


E CHE
“L’ACCESSO ALLA QUANTITÀ”
SI BASA ANCHE
SU ALTRE CAPACITÀ/ABILITÀ
SPECIFICHE CHIAMATE
“SUBITIZING”
CIOÈ
IL RICONOSCIMENTO VISIVO
INTUITIVO E “IMMEDIATO”
DELLA QUANTITÀ/NUMEROSITÀ


IN COSA CONSISTE IL CONTARE?

METTERE IN
CORRISPONDENZA BIUNIVOCA
GLI ELEMENTI “DA CONTARE”
CON GLI ELEMENTI
CHE “CONTANO”


DALLE TACCHE SUGLI ALBERI

AI “CALCULI”


DAI CALCULI…ALLE MANI

0 1 2 3 4 5 6


“CONTARE” E “NUMERARE”
IL LIVELLO “SEMANTICO”

SUBITIZING 13

24/11/2011 R. Imperiale, DISCALCULIA
13 160

IL SISTEMA DI CALCOLO
SE SI VUOL CONOSCERE IL NUMERO TOTALE DI ELEMENTI
CONTENUTI UN UN INSIEME OTTENUTO
UNENDO DUE ALTRI INSIEMI
SI SCOPRE CHE IL SEMPLICE CONTARE NON BASTA PIÙ.
SUPPONIAMO INFATTI DI VOLER CONOSCERE
QUANTI ELEMENTI CONTIENE
“UN CONTENITORE TRASPARENTE”
NEL QUALE “VENGANO INTRODOTTI”
PRIMA 5 ELEMENTI E POI ALTRI 3
AD ES. 5 PALLINE ROSSE E 3 BLU …


PROCEDEREMO COSÌ…

3
1
4
6
C
7
8
2 5

1. CONTEREMO QUELLE CHE ERANO
LE PALLINE DI A
(ROSSE…)
…E PROSEGUENDO
2. CONTINUEREMO A CONTARE LE PALLINE DI B (BLU…)
AGGIUNGENDOLE DI FATTO A QUELLE DI A


Così facendo…

ABBIAMO OTTENUTO LA RISPOSTA:
8 PALLINE
ATTRAVERSO L’OPERAZIONE DI
ADDIZIONE


QUESTO CI PORTA A DIRE CHE…

L’ADDIZIONE
E’
“IL CONTINUARE A CONTARE”
“VERSO DESTRA”


INFATTI, COM’E’ NOTO…
LA RETTA DEI NUMERI INTERI
E’ ORIENTATA
DA SINISTRA A DESTRA
0

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

ESSENDO LO “ZERO” UNA SORTA
DI MURO INSUPERABILE A SINISTRA
CHE PERO’ PRIMA O POI SGRETOLEREMO

DI SEGUITO…

LA SOTTRAZIONE
E’
“IL CONTINUARE A CONTARE”
“VERSO SINISTRA”


ESEMPIO

5-3=2
IL RISULTATO SI OTTIENE
ATTRAVERSO UN’AZIONE
DEL GENERE
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15


Come la neve al sol si disigilla
Così al vento nelle foglie lievi
Si perdea la sentenza di Sibilla…
(Paradiso, canto 33°, vv. 64-66)

IL RESPONSO E LE STRANE ANALOGIE

IBIS, REDIBIS, NON MORIERIS IN BELLO

IBIS, REDIBIS NON, MORIERIS IN BELLO


CHE NE DITE
DI QUESTA DISUGUAGLIANZA?

(10 – 7) – 2 ≠ 10 – (7 – 2)
Nei libri di testo c’è scritto che
LA SOTTRAZIONE NON GODE
DELLA PROPRIETA’ ASSOCIATIVA


ORA VEDREMO UNA STRANA TABELLA….

CHE TUTTAVIA CI SERVIRÀ
A MOLTIPLICARE
(SOMMARE RIPETUTAMENTE)
AD ESEMPIO
25 x 19

ESSA È COSTRUITA COME SEGUE:
SULLA COLONNA SINISTRA
1 25
PONIAMO
2 50 LE POTENZE DEL NUMERO 2
SULLA COLONNA DI DESTRA
4 100 UNO DEI DUE FATTORI,
8 200 IN GENERE IL MAGGIORE
E A SEGUIRE IL PRODOTTO
16 400 DI QUEL FATTORE
PER OGNUNA DELLE POTENZE
32 800 DI DUE


PER ESEGUIRE 19 X 25 OPERIAMO COME SEGUE

1 25
POICHÉ 19 = 16 + 2 +1
2 50 GUARDIAMO IN CORRISPONDENZA
DI ESSI
4 100 QUALI SIANO
8 200 I MULTIPLI DI 25 CORRIPONDENTI
E SOMMIAMOLI
16 400 OTTERREMO
400 + 50 + 25 = 475
32 800 IL CONTROLLO CONFERMA


STRANA TABELLA….
CHE TUTTAVIA CI SERVIRÀ A DIVIDERE
(SOTTRARRE RIPETUTAMENTE)
– QUANDO SIA POSSIBILE -
UN NUMERO PER UN ALTRO
AD ESEMPIO
240 : 12

STESSA PROCEDURA…SUL DIVISORE

1 12
2 24
4 48
8 96
16 192
32 384


PER ESEGUIRE 240:12

1 12
2 24 POICHÉ 240 = 192 + 48
GUARDIAMO QUALI SIANO
4 48 LE POTENZE DI 2 CORRISPONDENTI
8 96 E SOMMIAMOLI
OTTERREMO
16 192 16 + 4 = 20
IL CONTROLLO CONFERMA
32 384


DIAGRAMMA DELLE OPERAZIONI

CONTARE

ADDIZIONE SOTTRAZIONE

MOLTIPLICAZIONE DIVISIONE

MA, DI PIÙ…

NOI ABBIAMO
A DISPOSIZIONE
UNA FAMOSISSIMA
TABELLA

X 0 1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 10
2 0 2 4 6 8 10 12 14 16 18 20
3 0 3 6 9 12 15 18 21 24 27 30
4 0 4 8 12 16 20 24 28 32 36 40
5 0 5 10 15 20 25 30 35 40 45 50
6 0 6 12 18 24 30 36 42 48 54 60
7 0 7 14 21 28 35 42 49 56 63 70
8 0 8 16 24 32 40 48 56 64 72 80
9 0 9 18 27 36 45 54 63 72 81 90
10 0 10 20 30 40 50 60 70 80 90 100

CHE SI PUÒ “USARE” SIA PER MOLTIPLICARE
(4 x 3 = 3 x 4)

X 0 1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 10
2 0 2 4 6 8 10 12 14 16 18 20
3 0 3 6 9 12 15 18 21 24 27 30
4 0 4 8 12 16 20 24 28 32 36 40
5 0 5 10 15 20 25 30 35 40 45 50
6 0 6 12 18 24 30 36 42 48 54 60
7 0 7 14 21 28 35 42 49 56 63 70
8 0 8 16 24 32 40 48 56 64 72 80
9 0 9 18 27 36 45 54 63 72 81 90
10 0 10 20 30 40 50 60 70 80 90 100


CHE PER DIVIDERE…
(20 : 4)

X 0 1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 10
2 0 2 4 6 8 10 12 14 16 18 20
3 0 3 6 9 12 15 18 21 24 27 30
4 0 4 8 12 16 20 24 28 32 36 40
5 0 5 10 15 20 25 30 35 40 45 50
6 0 6 12 18 24 30 36 42 48 54 60
7 0 7 14 21 28 35 42 49 56 63 70
8 0 8 16 24 32 40 48 56 64 72 80
9 0 9 18 27 36 45 54 63 72 81 90
10 0 10 20 30 40 50 60 70 80 90 100


PRIMA DI PROCEDERE ACCENNIAMO
ALL’EMBODIMENT

TERMINE CHE POSSIAMO
LIBERAMENTE TRADURRE CON

«IMPARARE ATTRAVERSO IL CORPO»


CHE VUOL DIRE
CHE IL CORPO È MEDIATORE
E STRUMENTO «PRIMO»
DI OGNI NOSTRO ATTO
DI CONOSCENZA
…E IL GIOCO L’AMBIENTE
CHE PIÙ DI OGNI ALTRO
FAVORISCE L’IMPARARE

DEL RESTO, UN INSOSPETTABILE EMPIRISTA
FECE PROPRIO L’ASSIOMA PERIPATETICO

NIHIL EST NULLA È
IN INTELLECTU NELL’INTELLETTO
QUOD PRIUS CHE PRIMA
NON FUERIT NON SIA STATO
IN SENSU NEI SENSI
TOMMASO D’AQUINO

CHE, CON LE DOVUTE PROPORZIONI,

SINTETIZZA BENE

CIÒ CHE VOGLIAMO DIRE


ALLORA: CONTIAMO ALL’INDIETRO?


ANDIAMO A PASSEGGIO

SUL ROSSO E SUL BLU


CONTARE IN “AVANTI-DESTRA”
È “PIÙ FACILE”
CHE NON CONTARE IN “INDIETRO-SINISTRA”

PERCHÉ
IL CERVELLO È ASIMMETRICO
E
LO SPAZIO È ORIENTATO
DA SINISTRA A DESTRA
E QUINDI OCCORRE – PER COSÌ DIRE –
RISIMMETRIZZARLO


PRENDIAMO SPUNTO…

DA UN GIOCO
CHE ORA VI RACCONTO


E CHE MI FECE PENSARE…

ALL’ATTIVITÀ
CHE SEGUE


DESTINAZIONE
I NOSTRI RAGAZZI
CON PROBLEMI DI ORIENTAMENTO
SPAZIO-TEMPORALE
NEGOZIAZIONE:
DESTRA-SINISTRA
RELATIVE E ASSOLUTE
I BRACCIOLI COLORATI
E LO SPAZIO ROSSO-BLU

Così…

“i passi avanti / indietro” dei giocatori di Regina Reginella
diventarono
la parte BLU
e
la parte ROSSA

di qualsiasi “cammino” sul quale
è “la stessa cosa” muoversi
in un verso o nell’altro.

PRIMO PASSO

MUTARE
AVANTI-DIETRO
IN
SINISTRA-DESTRA


QUINDI

(dopo aver colorato il cammino di blu e di rosso)
individuato su di esso un punto di partenza P

P

ci si poteva muovere andando a DESTRA o a SINISTRA
“seguendo” ad es. istruzioni del tipo:

3

3

Ottenendo il seguente effetto:

3
P
e poi, RIPARTENDO da P
3
P

in definitiva, questo:
P


Fin qui…

niente di nuovo…
anzi, banale e facile da “fare”.
Per “andare avanti” bisogna fare
un “salto logico”
chiedendo ai bambini di eseguire
DI SEGUITO
le istruzioni a frecce del tipo
appena esaminato.


La richiesta si esaudisce abbastanza facilmente…

quando le istruzioni sono per es. del tipo:
3 2
oppure
2 3
Infatti, i percorsi si eseguono così
P
oppure
P


Il problema sorge…

quando si chiede ai ragazzi
di eseguire
istruzioni
con frecce di
colore diverso


chiedendo loro di eseguire
DI SEGUITO
ad esempio, un percorso del tipo:
2
4
che porterebbe al risultato seguente

P


Ma, tutto ciò…

non è affatto facile.
Perché – si chiedono i ragazzi-
un’istruzione
ROSSA
si deve eseguire
sulla parte
BLU ?


Si evidenzia così il contrasto…

tra la facilità di esecuzione
di un percorso costituito da istruzioni
DELLO STESSO COLORE
e la difficoltà di esecuzione
di un percorso costituito da istruzioni

di

COLORE DIVERSO

Allora...

ricordando che nel gioco ripartivi da
“dove eri arrivato il turno prima”
cosa che regola il «di seguito»
si chiede di “negoziare”

l’ulteriore definitivo

“salto logico”:

Quando le istruzioni hanno DIVERSO COLORE

il colore della seconda istruzione
IN PIU’ SIGNIFICA :

“PRIMA DI ESEGUIRMI RICORDATI

DI FARE MEZZO GIRO SU TE STESSO

E POI DI FARE IL NUMERO DI PASSI CHE DEVI”


Superato questo “scoglio”…

si può cominciare a far notare

ciò che accade in questo caso.


Dopo aver effettuato, supponiamo,
il percorso
2
4
il punto di arrivo viene a trovarsi
nella “zona rossa” a 2 passi (ROSSI)
dal punto di partenza P


Da qui in avanti…

il lavoro può ampliarsi.
Si “sdoppia” – per così dire –
la retta orizzontale bi-orientata:
SINISTRA-DESTRA
se ne fa ruotare la sua “gemella”
di 90° antiorari,
inducendo il bi-orientamento
ALTO-BASSO


Ottenendo questo “effetto”

P


Per i nostri scopi…
è importante ora costruire un quadrettato
(come nei giochi: “battaglia navale”,ecc…)
su cui poter effettuare percorsi “a frecce”

P


Per esempio,il percorso seguente:

3 3 5 5 2 2


O il percorso seguente:

3 3 5 5 3 3


Dei due percorsi visti…

il PRIMO possiamo definirlo
CHIUSO
perché il punto d’arrivo coincide
col punto di partenza
mentre il SECONDO
lo diremo
APERTO
perché i due punti non coincidono.


DOMANDA:

E’ possibile - in modo univoco -
assegnare ad ogni percorso
un numero
magari “colorato”
che – come un’etichetta -
lo descriva
e
che ne descriva le caratteristiche?

PRIMA RISPOSTA:

Nei percorsi CHIUSI
punto d’arrivo e punto di partenza coincidono.
Inoltre
i passi ROSSI (sinistra-basso)
sono esattamente quanto
i passi BLU (destra-alto).
In modo “quasi naturale”
diciamo che il numero-etichetta
dei percorsi CHIUSI…
è lo ZERO.

SECONDA RISPOSTA:

Nei percorsi APERTI
punto d’arrivo e punto di partenza
non coincidono
ei
passi ROSSI (sinistra-basso)
sono in numero diverso dai
passi BLU (destra-alto).
Vedremo che il numero-etichetta dei percorsi APERTI
varia a seconda della posizione
del punto di arrivo sul piano.

Asseriamo che

per individuare il “numero-etichetta” di ogni percorso
bisogna eseguire
in orizzontale-verticale
IL PERCORSO MINIMO
che porti dal punto di partenza P
al punto d’arrivo di quel percorso
e poi
SOMMARE ALGEBRICAMENTE
i passi/colore.
(che in seguito chiameremo COORDINATE del punto)

Per mostrare quello che intendiamo

Fissiamo sul piano alcuni punti di arrivo
di “percorsi aperti”
ed assumiamoli
come
PUNTI-EMBLEMA


Ad esempio…

i seguenti 8 PUNTI-EMBLEMA

P

che avranno ovviamente colore diverso…

proprio perché…
Ogni punto del piano si raggiunge da P
attraverso un percorso minimo orizzontale-verticale
(cioè dei passi-colore che “caratterizzano” quel punto)
quale che sia l’effettivo percorso che vi termini

3 2

1
4

P
8

5
7

6


Infatti, ad esempio, costruito il quadrettato
Il punto 1 si raggiunge col percorso minimo
2 2
Il punto 5 col percorso
3 2
Cosa vuol dire? Quali sono gli altri percorsi minimi?

3 2

1
4

P
8

5
7

6


Vediamo…
3 3
4 4
Cosa vuol dire tutto ciò?

3

P

7


E ancora…
2 4
4 1
Cosa vuol dire? Cosa accade ai punti 6 e 8 ?

3 2

1
4

P
8

5
7

6


Domanda fondamentale
I punti del 1° quadrante son tutti BLU ?
I punti del 3° quadrante son tutti ROSSI ?
Cosa succede - invece - nel 2° e 4° quadrante ?

3 2

1
4

P
8

5

7
6


Un’altra domanda fondamentale
C’è per caso relazione tra i punti 1, 2 e 8 ?
E tra i punti 3 e 7 ?
E tra 4, 5 e 6 ?

3

1
4 2

P
5 8

7
6


Possiamo costruire il diagramma seguente…(incompleto)?

P

2
1
0
1
2

eccetera eccetera eccetera

E infine “appiattendo” le rette
su quella orizzontale

.. 4 3 2 1 0 1 2 3 4 ..
eccetera eccetera eccetera…


RISOLVERE PROBLEMI


PORSI PROBLEMI E – SOPRATTUTTO –
“RISOLVERE PROBLEMI
SI PUO’ CONSIDERARE
L’ATTIVITA’ PIU’ CARATTERISTICA
DEL GENERE UMANO”
(G. Polya, Come risolvere i problemi di matematica, Feltrinelli, Milano, 1993)


Ed ecco il problema d’una povera lumaca…
Una lumaca deve scalare un muro alto 11 metri.
Di giorno sale di 4 metri, di notte scende di 3 metri.
Quanto impiegherà per giungere in cima al muro?

ANALIZZARE
I DUE PUNTI DI VISTA


SOLUZIONE
SOLUZIONE NON-STANDARD
O DELLA DIVERGENZA
RISPOSTA STANDARD

(4-3)x11=11

RISPOSTA NON STANDARD: 1 2 3 4 5 6 7

7 giorni e ½ e infine
24/11/2011 R. Imperiale, DISCALCULIA 7 + 4 = 11 229

SOLUZIONE
“PASSO DOPO PASSO”
O
“EURISTICA”
“dal greco: ευρισκω,
“scopro, trovo”


LA GENERALIZZAZIONE
E
I SUOI ERRORI


PRIMO PROBLEMA…

Posseggo due monete.
la loro somma è 3 €.
Una delle due monete NON È 2 €.
Quanto vale ciascuna delle due monete
che posseggo?

?€ ?€
Il problema ammette soluzione?

SOLUZIONE

UNA DA…
1€
E UNA DA…
2€

E ancora…

In un incidente stradale il padre muore sul colpo,
mentre suo figlio, pur gravemente ferito, si salva.
Viene condotto in ospedale per essere operato;
ma non appena il chirurgo lo vede esclama:

Oh no! Non posso
operarlo…
…questo è mio
figlio…!
figlio…!

E’ possibile tutto ciò?

E’ POSSIBILE…
IL CHIRURGO
E’ LA MADRE
DEL RAGAZZO


UN COMPITO…
IN CLASSE
O UN COMPITO…
DI CLASSE?


PROBLEMA

RISOLVERE IL TRIANGOLO
c = 10
a + b = 5 ( 3 + 1)


PROBLEMA: QUALE TRIANGOLO?
QUESTO

O
QUESTO ?


CI PENSA IL PROFESSORE…TRAMITE LIBRO DI TESTO

c = 10
a + b = 5 ( 3 + 1)
SUGGERIMENTO: PORRE
a = c cos β
b = c sen β

AH! BHÉ!…

ALLORA È UN TRIANGOLO RETTANGOLO…

α
c
b

β

90° β
a

PERCHE’…

LE DUE RELAZIONI
a = c cos β
b = c sen β
VALGONO SOLO SE IL TRIANGOLO
È – APPUNTO -
RETTANGOLO

MA ALLORA…
SE DI TRIANGOLO RETTANGOLO SI TRATTA
c = 10
SARÀ – COME DA TEOREMA SUGGERITO -
L’IPOTENUSA
E, QUINDI
a, b
LEGATI DALLA RELAZIONE

a + b = 5 ( 3 + 1)
SARANNO I CATETI

DA QUI IN POI…
POSSIAMO COMINCIARE A “DIVERTIRCI”
CIOÈ A “CAMBIARE STRADA” (“DI-VERTERE”)
A “IMMAGINARE”, ANCHE SE

“Nella scuola italiana l’immaginazione
occupa la stessa posizione di Babbo Natale,
viene una volta all’anno, al dì di festa”

(L. Marchetti, L’umanesino e i compiti di una scienza ≪nuova≫ della formazione;
≫
in (a cura di P. Bevilacqua): A che serve la storia, Donzelli, Roma, 2011)


MA NOI NON DEMORDIAMO…
POSSIAMO PER CASO “IMMAGINARE”
CHE SI POSSA SCRIVERE:

a + b = 5 3+ 5
E, QUINDI

a=5 3 E b=5
O QUALCOSA DI SIMILE?


PER PROVARLO…

DOBBIAMO VERIFICARE
UNA “CERTA” RELAZIONE

c2 = a 2 + b2


COMINCIAMO…
c2 = 102 = 100

a 2 = (5 3 )2 = 75

b2 = 52 = 25
E FINIAMO… c2 = a 2 + b 2

DUNQUE È PROPRIO
QUEL CHE ABBIAMO IMMAGINATO…

a=5 3
b=5


QUESTO CI PORTA IMMEDIATAMENTE A DIRE CHE IL TRIANGOLO…
OLTRE AD ESSERE RETTANGOLO…

30°
5 3 10
β

90° 60°
5
È ANCHE METÀ DI UN TRIANGOLO EQUILATERO
(perché….5 è la metà di 10)
QUINDI…

COSÌ IL PROBLEMA
c = 10
a + b = 5 ( 3 + 1)
È … RISOLTO
SENZA FAR RICORSO AD AMBITI ALTRI


MA IL PROBLEMA…
ERA
NEL CAPITOLO
“TRIGONOMETRIA”…
QUINDI BISOGNAVA DISTURBARE
IL SENO E IL COSENO…


NOI INVECE ABBIAMO USATO
LA PROPRIETÀ RAFFIGURATA
IN QUESTO “DISEGNO”…
A A

B
D B D

C C


QUESTA…

…CHE ABBIAMO APPENA VISTO
COM’È NOTO
È UNA – LA - DIMOSTRAZIONE DEL
“CELEBRE PROBLEMA DI PITAGORA”
CHE SI COMPRENDE SOLO
SE SI È CONSOLIDATO UN PRINCIPIO…

DOVE C’È PIÙ ERBA?

A QUESTA DOMANDA SI RISPONDE:
SOTTRARRE FIGURE “UGUALI”
DA FIGURE “UGUALI”
IN GENERE GENERA
FIGURE “EQUIVALENTI”

DOVE C’È PIÙ ERBA?

QUALCUNO, AL DI LÀ DEL PERCEBIBILE
DIREBBE ANCHE CHE
SI CONSERVANO
LE QUANTITA’ DISCRETE


PER CURIOSITÀ…

DIMOSTRAZIONE DEL TEOREMA DI PITAGORA
DATA DA
JAMES GARFIELD (1831-1881),
XX° PRESIDENTE DEGLI STATI UNITI D’AMERICA


B
D
z
y z x

x y E
A C
l’area del trapezio ABDE è

( x + y)( x + y)
2
ma anche

x y + z2/2

Quindi
( x + y)( x + y)
= x y + z2/2
2
CIOÈ:
x2 + 2xy + y2 = 2xy + z2

DA CUI DERIVA

x 2+ y 2= z 2

MA, PER TORNARE AI NOSTRI PROBLEMI….

3
CHI È?
…SARÀ UGUALE A QUALCOSA ?

PROVIAMO A RISPONDERE
1 COSTRUENDO
1
LA SEGUENTE SPIRALE…
1
3 4 1
2
1 5
90°
1 6

E COSÌ VIA
ORA CHIEDIAMOCI:
QUANTO È LUNGO IL SEGMENTO ROSSO ?
COME S’È VISTO … È “FACILE” A DIRSI: 3


BHÉ…!

ANCORA NON SAPPIAMO CALCOLARE 3

MA ALMENO…

L’ABBIAMO VISTO…


COM’È NOTO:

3
È UN IRRAZIONALE COSÌ COME

2
CHE HA DATO TANTI…PROBLEMI

LE PARENTELE
IMPREVISTE


ANCORA…PROBLEMI! ABBIAMO SETTE PANI

COME FACCIAMO A DIVIDERLI
TRA DIECI PERSONE?
24/11/2011
QUANTO TOCCA A CIASCUNA?

PRIMA IPOTESI
RICORRIAMO AD UN MIRACOLO

SEBBENE DI MODESTE DIMENSIONI

RISPETTO AD ALTRI

PIÙ CELEBRI E PIÙ MIRACOLI

SECONDA IPOTESI

PRENDIAMO ATTO

DEI NOSTRI LIMITI

E COMINCIAMO A “PENSARCI”


MA SENZA QUELLA FRETTA…
CHE CI “OBBLIGHEREBBE”
A RISPONDERE IMMEDIATAMENTE:

7
10

CHE È LA RISPOSTA “OVVIA”

MA NON QUELLA
“NEGOZIATA”

NEGOZIAMO
PRIMA DOMANDA:
COME DEVONO ESSERE TRA LORO
LE PARTI NELLE QUALI
RISULTERANNO “DIVISI” I PANI?
RISPOSTA OVVIA (O NON TANTO…?)


NON TANTO…SOPRATTUTTO SE…
NEL PROBLEMA
QUESTA OVVIETÀ
NON VENGA ESPLICITATA
INFATTI ESSA È
- FORSE – IMPLICITAMENTE ACCETTATA
MA BISOGNA COMUNQUE ACCERTARSENE
PERCHÉ NON SEMPRE
L’IMPLICITO…RISULTA FAMILIARE….

SOPRTATTUTTO SE ESSO…
SIA STATO OGGETTO
DI DIDATTICA
A SUA VOLTA IMPLICITA…
OVVERO LO SI SIA DATO
“PER SCONTATO”


SI VEDA INFATTI QUESTO PROBLEMA

QUAL È ILNUMERO MASSIMO DI PARTI IN CUI
RISULTA DIVISA UNA TORTA CIRCOLARE

DA TRE TAGLI RETTILINEI
EQUIVALENTI A TRE CORDE?

SOLUZIONE ?


O SOLUZIONE ?


DEL RESTO….
UN SASSO LANCIATO CONTRO UN VETRO
LO IN-FRANGE IN
“MILLE” PEZZI
CIASCUNO DEI QUALI
È – QUINDI - UNA “FRAZIONE”
MA CON UNA PROBABILITÀ QUASI NULLA
DI ESSERE
“UGUALE AD UN ALTRA”

CHE FIGURA SI OTTIENE
CONGIUNGENDO I PUNTI

6 1

5 2

4 3


CHE FIGURA SI OTTIENE
CONGIUNGENDO I PUNTI

6 1

5
2
4 3


IN ENTRAMBI I CASI
LA FIGURA È UN ESAGONO

REGOLARE, NEL PRIMO CASO

IRREGOLARE, NEL SECONDO


DA COSA DIPENDE?
OVVIO:
NEL PRIMO CASO
LE TRE CORDE DIVIDONO IL CERCHIO
IN PARTI “UGUALI”
NEL SECONDO, NO…

NEGOZIARE
AMPIEZZA
DI UN SETTORE CIRCOLARE
AREA DI UN SETTORE CIRCOLARE
FRAZIONI EQUIVALENTI
2
1


NEGOZIARE

LA FRAZIONE È…
1. “RAPPORTO”
2. OPERATORE
3. NUMERO
4. NUMERO DI NUMERO

LA FRAZIONE COME

RAPPORTO


NEGOZIARE

LA FRAZIONE GENERATRICE…

CON RACCONTO
PERCHÉ SI METTE IL 9
AL DENOMINATORE?


PERCHÉ

1 2 3 4
= 0,1 = 0,2 = 0,3 = 0,4
9 9 9 9

E COSÌ VIA….FINO A

9
= 0,9 …… OPPURE = 1 ?
9

Il numero 6, 2

Si può anche scrivere
6,2222 ………
Ponendo x = 6,2222…
Sarà 10x = 62,2222…
E quindi
10x – x = 62,2222…- 6,2222… = 56
Cioè 9x = 56, quindi

56
X =
9

Il numero 1,23456
Si scrive anche
x = 1,23456456456…
100x = 123,456456456…
100000x = 123456,456456456…
100000x – 100x = 123456 - 123
Cioè 99900x = 123456 – 123 = 123.333
E quindi

123456 − 123 123333
X = =
99900 99900

IL COMBINARE


DOMANDA
IN QUANTI MODI SI PRESENTA
IL LANCIO CONTEMPORANEO DI DUE MONETE?
COM’È NOTO, CÀPITA CHE :

LA PRIMA MONETA
MOSTRI DUE MODI: T-C
PER OGNUNO DI QUESTI CASI
LA SECONDA MONETA
MOSTRA DUE MODI : T-C

IN DEFINITIVA:

T QUINDI
T IL LANCIO
C CONTEMPORANEO
DI DUE MONETE
T SI PRESENTA IN 4 MODI
C 1. T – T
C 2. T – C
3. C – T
4. C – C

VI RICORDATE CHE ABBIAMO DETTO CHE SE…
a, b FOSSERO RISPETTVAMENTE «TESTA» E «CROCE»
LA «FRASE» (a + b)2 = a2 + 2 a x b + b2
SAREBBE LO SPAZIO-EVENTI
DEL LANCIO CONTEMPORANEO DI DUE MONETE, CIOÉ

a b

a b a b

a2 ab ba b2
2 TESTE, 1TESTA-CROCE, 1 CROCE-TESTA, 2 CROCI
OVVERO, GLI APPENA VISTI «QUATTRO MODI POSSIBILI»
IL CUI NUMERO SI OTTIENE ANCHE SOMMANDO I COEFFICIENTI
1, 2, 1,……CHE COMPAIONO NELLA «FRASE»?

UN…RICORDO CHE RIAFFIORA (NEWTON?)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

ECC…


E CHE CI DICE CHE
1 1
1 1 2
1 2 1 4
1 3 3 1 8
1 4 6 4 1 16
ECC…

CIOÈ, (a+b)n
a b

QUESTO È IL NOTO TRIANGOLO DI….?
1
1 1
TRA L’ALTRO
1 2 1 INVENTORE
DELLA
1 3 3 1 PASCALINA

1 4 6 4 1
ECC…

PASCAL

E QUEST’AFFARE COS’È?
LA MACCHINA DI GALTON
È UN DISPOSITIVO INVENTATO DA F. GALTON
PER DIMOSTRARE IL TEOREMA DEL LIMITE
CENTRALE E VISUALIZZARE LA DISTRIBUZIONE
NORMALE. CONSISTE IN UN PIANO SUL QUALE
SONO PIANTATI DEI CHIODI. DA UNA FESSURA,
POSTA IN CIMA A TALE PIANO, VENGONO
FATTE CADERE DELLE PALLINE (CHE,
TOCCANDO I CHIODI, SI DIRIGONO VERSO
LA MACCHINA DI GALTON DESTRA O VERSO SINISTRA). SUL FONDO
SONO COLLOCATI DEI CONTENITORI
CILINDRICI, DOVE LE PALLINE SI DEPOSITANO
L'UNA SULL'ALTRA, FORMANDO DELLE PILE, LE
CUI ALTEZZE ASSUMONO ALL’INCIRCA LA
FORMA DI UNA CURVA A CAMPANA. ALLE
TESTE DEI CHIODI SI PUÒ SOVRAPPORRE
PERFETTAMENTE IL TRIANGOLO DI PASCAL.

TRIANGOLO DI PASCAL

MACCHINA DI GALTON

PER CHI NE VOGLIA SAPERE DI PIÙ

n k (1 – p)n-k
 
k p
 

QUESTA È LA FUNZIONE DI PROBABILITÀ
DELLA DISTRIBUZIONE BINOMIALE


DIAGRAMMI AD ALBERO…
TABELLE A DOPPIA ENTRATA…

STRUMENTI PER DESCRIVERE…
PER ANALIZZARE…
PER GIOCARE…

CHISSÀ SE L’ANNO VENTURO
SARÒ GRANDE ABBASTANZA
PER GOCARE CON LE PAROLE
DI QUATTRO LETTERE…

A VIGNETTA…
M PEDAGOGICA

0

IL PROBLEMA DEGLI ANAGRAMMI

L’ANAGRAMMA
TRASFORMA UNA PAROLA IN UN’ALTRA
(NON NECESSARIAMENTE DI SENSO COMPIUTO)
E SI OTTIENE
PER SPOSTAMENTO (TOTALE O PARZIALE)
DELLE LETTERE DI QUELLA PAROLA


QUINDI, AL DI LA’ DEL SIGNIFICATO, SI CHIEDE, AD ESEMPIO:

QUANTI SONO
TUTTI GLI ANAGRAMMI
DI UNA PAROLA
DI 4 LETTERE?


PER RISPONDERE RAGIONIAMO COME SEGUE
1. AL PRIMO POSTO POSSIAMO INSERIRE OGNUNA
DELLE 4 LETTERE CHE COMPONGONO LA NOSTRA PAROLA
2. PER OGNUNA DI ESSE AL SECONDO POSTO
POSSIAMO INSERIRE CIASCUNA DELLE 3 LETTERE RESIDUE
3. PER OGNUNA DI ESSE AL TERZO POSTO
POSSIAMO INSERIRE CIASCUNA DELLE 2 LETTERE RESIDUE
3. PER OGNUNA DI ESSE AL QUARTO POSTO
POSSIAMO INSERIRE L’ULTIMA LETTERA RESIDUA

4 3 2 1
X X X

IN DEFINITIVA

TUTTI GLI ANAGRAMMI
DI UNA PAROLA
DI 4 LETTERE
SONO 24


CONSIDERIAMO AD ESEMPIO LA PAROLA….

ROMA


E VEDIAMONE I PRIMI SEI…..

M A
O
A M
O A
R M
A O
O M
A
M O


PER ESERCIZIO

COSTRUIRE
LO SCHEMA
COMPLETO

IL METAGRAMMA O DOUBLET
QUESTO GIOCO, INVENTATO DA CHARLES DODGSON, IL CUI
PSEUDONIMO ERA LEWIS CARROLL - DICE NULLA IL NOME?
– E ALICE NEL PAESE DELLE MERAVIGLIE DICE NULLA? –
CONSISTE NEL PRENDERE DUE PAROLE CHE ABBIANO TRA
LORO UNA QUALCHE ATTINENZA E LO STESSO NUMERO DI
LETTERE (LA STESSA LUNGHEZZA…); E PASSARE DA UNA
ALL’ALTRA ATTRAVERSO IL CAMBIO DI UNA LETTERA PER
VOLTA. È VIETATA LA PRESENZA CONTEMPORANEA DI
MASCHILE E FEMMINILE, SINGOLARE E PLURARE. VINCE
CHE PASSA DA UNA ALL’ALTRA DELLE DUE PAROLE SCELTE
COL MINOR NUMERO DI PASSI. UNA CURIOSITÀ…MICA
TANTO…: DODGSON ERA PROFESSORE DI MATEMATICA E DI
LOGICA…!

METAGRAMMA

SOLE
SALE DUE
SALA
SANA
TUE
LANA TRE
LUNA

Come si fa a mettere il

POLLO nel FORNO
?


così
POLLO
COLLO
CALLO
CARLO
CARRO
CORRO
CORNO
FORNO

METAFONOLOGIA
SILLABA FINALE/INIZIALE
GIOCO DEL DOMINO

PE-RA RA-NA NA-VE VE-LA LA-NA NA-SO


Dal: Musikalisches Wurfelspiel K516f
di


SEMPRE PROBLEMI….


SALVAR CAPRA E CAVOLO
Un contadino abita in una piccola casetta, al di qua del
ruscello. Per sfamarsi, coltiva dei cavoli in un campicello al di
là di esso; ogni sera se ne porta uno con sé. Nella stalla vicino
alla sua casetta, inoltre, alleva una capra che gli dà il latte; e ci
tiene un lupo per sua difesa: legati, e lontani l’uno dall’altra.
Ogni mattina, per andare al campo, passa il fiume su una
piccola e sgangherata barchetta che può portare – oltre a lui –
solo un altro “essere”: o il lupo, o la capra o il cavolo. Fin qui la
cosa è facile: conduce al campo prima il lupo e poi la capra,
perché sarebbe un grave errore portarvi la capra stessa prima
del lupo, per via del feeling dell’ovino con le povere
brassicacee. Al mattino, quindi, nessun problema, per
nessuno. Ma, giunto a sera, come farà il contadino a tornare
nella sua casetta, salvando capra e cavolo ?
(Alcuino da York, Propositiones Alcuini Doctoris C.M.
Imperatoris ad Acuendos Juvenes)

SOLUZIONE: IL CONTADINO…
1. PORTA A CASA LA CAPRA
2. RITORNA AL CAMPO
3. PORTA A CASA IL LUPO
4. RITORNA AL CAMPO
RIPORTANDO CON SE’ LA CAPRA
5. LASCIA LA CAPRA AL CAMPO
E PORTA A CASA IL CAVOLO
6. RITORNA AL CAMPO
24/11/2011
7. RIPORTA A CASA LA CAPRA

IL PROBLEMA DEGLI OTTO SCOMPARTI

IN UNO DEGLI OTTO SCOMPARTI IN CUI È SUDDIVISA UNA SCATOLA
NASCONDIAMO UN OGGETTO.
DIRE QUAL È IL NUMERO MINIMO DI DOMANDE
– CUI SI POSSA RISPONDERE SOLAMENTE CON UN SI’ O CON UN NO –
PER ESSERE CERTI DI INDIVIDUARE
LO SCOMPARTO IN CUI L’OGGETTO È CELATO.

0 1 2 3 4 5 6 7


IL PROBLEMA DELLE PESATE

IN UN SACCHETTO CI SONO NOVE MONETE D’ORO
UNA DI QUESTE MONETE
CONTIENE MENO ORO DELLE ALTRE OTTO
E QUINDI PESA DI MENO.
QUAL E’ IL NUMERO MINIMO DI PESATE
MEDANTE LE QUALI POSSIAMO ESSERE SICURAMENTE CERTI
DI INDIVIDUARE LA MONETA FALSA
DISPONENDO DI UNA BILANCIA A DUE BRACCI?


COSA HANNO IN COMUNE
IL PROBLEMA DEGLI OTTO SCOMPARTI
ED IL PROBLEMA
DELLE PESATE CON UNA BILANCIA
A DUE BRACCI?


VEDIAMO
LE RISPETTIVE
SOLUZIONI


SOLUZIONE
DIVIDIAMO LA SCATOLA IN DUE PARTI A, B;
INDI CIASCUNA DI QUESTE IN DUE PARTI, A1, A2, B1, B2;
E INFINE OGNUNA DI ESSE ANCORA IN DUE PARTI. OTTERREMO:

0 1 2 3 4 5 6 7
A B
A1 A2 B1 B2
0 1 2 3 4 5 6 7
E DA QUI SI VEDE CHE “BASTANO” TRE DOMANDE PER SCOPRIRE L’OGGETTO.


DEL RESTO

SE DUE SONO LE POSSIBILI RISPOSTE
ALLE NOSTRE DOMANDE
PER RAGGIUNGERE OGNI SCOMPARTO
BASTANO 3 DOMANDE.
INFATTI

23= 8

LO SI VEDE ANCHE USANDO UN DIAGRAMMA AD ALBERO

1.a domanda

NO SI

2.a domanda

NO SI NO SI

3.a domanda
NO SI NO SI NO SI NO SI

0 1 2 3 4 5 6 7

0 = NO - NO - NO
COMPLETARE…….

ORA, INVECE CHE NO-SI USEREMO 0-1, OTTENENDO

1.a domanda

0 1

2.a domanda

0 1 0 1

3.a domanda
0 1 0 1 0 1 0 1

0 1 2 3 4 5 6 7

0 = 0–0–0
COMPLETARE…….

RISULTA CHIARO, ORA, PERCHE’ LE CASELLE SONO
STATE NUMERATE PARTENDO DALLO ZERO?
PERCHE’, SICCOME…

0=000 4=100
1=001 5=101
2=010 6=110
3=011 7= 1 1 1

ESSI RAPPRESENTANO
LA NOTAZIONE BINARIA
DEI NUMERI NATURALI
0, 1, 2, 3, 4, 5, 6, 7.


COSI’ FACENDO, PER ALTRO….

ABBIAMO Se, infatti, per qualche
ragione, rispondendo ad
una domanda, si dovesse

CREATO indicare una delle otto
caselle, potremmo certo
usare la notazione “araba”

UN “CODICE” ma anche la sua traduzione
binaria, che in più descrive
il percorso effettuato per
1. FINITO raggiungere la casella
detta.
2. NON AMBIGUO
3. IMPERATIVO


SOLUZIONE

EQUILIBRIO 1
4
4 SI È CERTO DEVOTI DI UN CELEBRE SANTO!

IL NUMERO MINIMO
SQUILIBRIO

DI PESATE
È 3…!

SQUILIBRIO
2 1
2 1

Quando si parte il gioco della zara,
Colui che perde si riman dolente,
Repetendo le volte, e tristo impara…
(Purgatorio, canto 6°, vv. 1-3)

LA ZARA È IL GIOCO DEI “TRE DADI”

PERCHE’ CONVIENE PUNTARE
SULl’ 11 E SUL 10 E NON SUL 9?


ALLA DOMANDA RISPOSE GALILEO GALILEI

11 (m) 10 (m) 9 (m)
641 6 631 6 621 6
632 6 622 3 531 6
551 3 541 6 522 3
542 6 532 6 441 3
533 3 442 3 432 6
443 3 433 3 333 1
27 27 25

L’ANALOGIA
dal greco
αναλογια
in italiano:
PROPORZIONE

PER ALCUNI AUTORI

L’ANALOGIA
E’ L’UNICA FORMA
DEL PENSIERO
E COINCIDE CON ESSO.

(D. Hofstadter)

LE METAFORE

AL MARE HO VISTO

“UN BOSCO DI OMBRELLONI”


L’ANALOGIA … E UN RACCONTO
Quanto è alta questa piramide..?
chiesero a Talete….

Ed egli rispose
sebbene
non avesse
altro su cui
CONTARE
se non
il suo bastone

L’ANALOGIA … E UN RACCONTO

L’OROLOGIO ANALOGICO
E LA STORIA DI UN “ERRORE…”


OSSERVANDO IL “CERCHIO” DEL SOLE
GLI ANTICHI SAPIENTI
AVEVANO “MISURATO”
IN 360 ALBE
E 360 TRAMONTI
IL TEMPO INTERCORRENTE
TRA DUE PASSAGGI
SUCCESSIVI DEL SOLE
SULLA VERTICALE
DI UN POZZO NEI PRESSI
DI ALESSANDRIA D’EGITTO
Pienza, città utopia


CONCLUDENDO CHE IL SOLE…

IMPIEGANDO, APPUNTO,
360 GIORNI
PER COMPIERE UN GIRO COMPLETO
SALISSE UN GRAD(IN)O AL GIORNO
(GRADIOR = IO SALGO)
DA QUI IL GRADO COME UNITÀ DI MISURA
DELL’ANGOLO GIRO
E L’ERRORE CHE ANCORA
“GIRA” NEL TEMPO.


TORNANDO…
…ALLA DIVISIONE
DEI SETTE PANI IN DIECI PERSONE
(PROBLEMA NR. 4 DEL PAPIRO)
E CON L’ESPLICITA RICHIESTA
CHE ESSI SIANO
EVANGELICAMENTE DIVISI
IN PARTI UGUALI
“COSTRUIAMONE LA PROCEDURA”

PER COMINCIARE I SETTE PANI
VENGONO DIVISI
24/11/2011
A METÀ

QUINDI SI COMINCIA LA DISTRIBUZIONE


RESTANO QUATTRO METÀ
DA SOLE INSUFFICIENTI
A SODDISFARE L’EVANGELICO COMPITO
QUINDI, ESSE VANNO A LORO VOLTA DIVISE
IN PARTI UGUALI
IN QUANTE PARTI
DOVREMO DIVIDERE CIASCUNA METÀ?

IN TANTE QUANTE SIANO SUFFICIENTI
PER ESSERE DISTRIBUITE
AI DIECI AFFAMATI SENZA SALTARNE ALCUNO…
QUINDI…IN TRE PARTI OGNUNA


DOPO L’ULTERIORE DISTRIBUZIONE,
RESTANO…


CHE, NATURALMENTE
VANNO DIVISE COME SI DEVE
LA VISIONE…
È INGRANDITA PER OVVIE RAGIONI
SULLE QUALI SARÀ UTILE UNA NEGOZIAZIONE
NEGOZIARE: “INGRANDIMENTO” – “RIDUZIONE”


COSA, DUNQUE,
È TOCCATO A CIASCUNO?

1 1 1 21
+ + =
2 6 30 30

COSA CHE, ABBONDANTEMENTE NOTA,
PUÒ SCRIVERSI COME SEGUE

21 7
=
30 10

IL PROBLEMA DEI 39 CAMMELLI
(DA: LE MILLE E UNA NOTTE)

UN RICCO ARABO, MORENDO, LASCIÒ AI SUOI 4 FIGLI
39 CAMMELLI E LA SEGUENTE INDICAZIONE:
1
DI ESSI DOVEVANO ANDARE AL PRIMO FIGLIO
2

1
DI ESSI DOVEVANO ANDARE AL SECONDO FIGLIO
4

1
8 DI ESSI DOVEVANO ANDARE AL TERZO FIGLIO
1
DI ESSI DOVEVANO ANDARE AL QUARTO FIGLIO

IN SOSTANZA

DATO CHE

1 1 1 1 39
+ + + =
2 4 8 10 40
SI TRATTA DI VEDERE SE SIA POSSIBILE
DIVIDERE
39 OGGETTI IN 40 PARTI UGUALI

COL METODO RHIND OTTERREMMO

1 1 1 1 1 1 39
+ + + + + =
2 4 8 16 32 160 40
MA QUESTO RISULTATO CONTRASTA CON LA VOLONTÀ
DEL PADRE
CHE VOLEVA DIVIDERE I SUOI CAMMELLI
TRA QUATTRO FIGLI


A MENO CHE IL PADRE NON SAPESSE CHE

1 1 1 1
+ + =
16 32 160 10
COME IMMAGINIAMO CHE SIA STATO

E SIA STATO DA LUI VOLUTO


CERTAMENTE CONOSCEVA BENE IL PROBLEMA
QUEL SAPIENTE CHE
GIUNTO IN GROPPA AL SUO CAMMELLO
E VEDENDO I FRATELLI DISCUTERE VANAMENTE
SI PROPOSE DI RISOLVERLO
AGGIUNSE IL SUO CAMMELLO AI 39 CHE DIVENNERO 40
NE DIEDE 20 AL PRIMO (UN MEZZO…)
10 AL SECONDO (UN QUARTO…)
5 AL TERZO (UN OTTAVO…)
4 AL QUARTO (UN DECIMO…)
POI, DATO CHE 20+10+5+4=39,
SI RIPRESE IL SUO E SE NE ANDÒ…

IL PROBLEMA DEI 35 CAMMELLI
UN PADRE, MORENDO, LASCIÒ AI SUOI 3 FIGLI
35 CAMMELLI E LA SEGUENTE INDICAZIONE:

1
2
DI ESSI DOVEVANO ANDARE AL PRIMO FIGLIO

1
DI ESSI DOVEVANO ANDARE AL SECONDO FIGLIO
3

1
DI ESSI DOVEVANO ANDARE AL TERZO FIGLIO
9

SOLUZIONE
UN SAGGIO GIUNTO IN GROPPA AL SUO CAMMELLO
E VEDENDO I FRATELLI LITIGARE
SI PROPOSE DI RISOLVERLO
AGGIUNSE IL SUO CAMMELLO AI 35, CHE DIVENNERO 36
NE DIEDE 18 AL PRIMO (UN MEZZO…)
12 AL SECONDO (UN TERZO…)
4 AL TERZO (UN NONO…)
POI, DATO CHE 18+12+4=34,
SI RIPRESE IL SUO
SCELSE TRA I 35 IL PIÙ BELLO E ROBUSTO
E SE NE ANDÒ…
MORALE: I LAVORI SI PAGANO…E BENE!


LE RUOTE
UNA MACCHINA DEVE PERCORRERE 500 Km
OGNI 100 Km
SI DOVRÀ MUTARE
LA POSIZIONE DELLE RUOTE
FACENDO ENTRARE NEL CAMBIO
ANCHE LA RUOTA DI SCORTA
QUANTI Km PERCORRERÀ OGNI RUOTA?

PROBLEMA
IL RETTANGOLO APPENA VISTO
È DIVISO IN 9 QUADRATI.
CALCOLARE LE SUE DIMENSIONI
SAPENDO CHE IL QUADRATO NERO
HA IL LATO LUNGO CM. 1.


PONIAMO X = LATO QUADRATO BIANCO
l. Q.B. = x
l. Q.Ve. = x+1
l. Q.Gi. = x+2 ;
l. Q.Gr. = x+3 ;
l. Q.A. = x+4-x = 4
l. Q. Az. = x+7;
l. Q.R. = 2x+1 ;
l. Q.Vi. = x+11

Viola+Azzurro=Rosso+Verde+Giallo

E QUINDI
Viola + Azzurro = Rosso + Verde + Giallo

x + 11 + x + 7 = 2x + 1 + x + 1 + x + 2

2x + 18 = 4x + 4

2x = 14

x=7

ecc….ecc…

CI SAREBBE MOLTO ALTRO DA DIRE, MA CI FERMIAMO
AUSPICANDO CHE GRAZIE A CIÒ – FORSE -
QUALCHE DIFFICOLTÀ, QUALCHE DISTURBO
QUALCHE “SEMPLICE” DISAGIO
SARANNO STATI SUPERATI
E I NOSTRI RAGAZZI
CI RINGRAZIERANNO SUBITO
O – MEGLIO - DOPO TANTI ANNI
DA ADULTI AD ADULTI
QUANDO LA RELAZIONE EDUCATIVA – SEMPRE RECIPROCA -
SI SARÀ DEFINITIVAMENTE SIMMETRIZZATA
PROPRIO COME ADESSO ABBIAMO FATTO CON LO SPAZIO FISICO
E COME ABBIAMO SEMPRE FATTO CON QUELLO DEGLI AFFETTI
GRAZIE!

PUGLIA - DSA e matematica - Imperiale

More Related Content

Similar to PUGLIA - DSA e matematica - Imperiale

More from Associazione Italiana Dislessia

PUGLIA - DSA e matematica - Imperiale