DSA_Big_O_ Data_Structure_and_Algorithm.pptx

© Dot Net Tricks Innovation Pvt. Ltd. | All rights Reserved.
Agenda
• What are Data Structures?
• Linear Data Structures
• Non-Linear Data Structures
• Common Data Structure Operations
• Abstract Data Types
• What is an Algorithm?
• Analysis of an Algorithm
• Asymptotic Notations
• Big-O Notations
• Problem Solving Techniques
DSA and Big-O

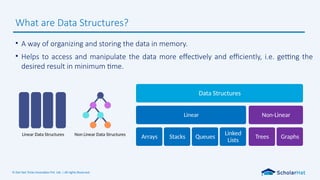
• A way of organizing and storing the data in memory.
• Helps to access and manipulate the data more effectively and efficiently, i.e. getting the
desired result in minimum time.
What are Data Structures?
Data Structures
Linear
Arrays Stacks Queues
Linked
Lists
Non-Linear
Trees Graphs
Linear Data Structures Non Linear Data Structures

• Arrange the elements in sequential or linear fashions.
• Each element is attached to its previous and next adjacent element.
• Static Data Structure has a fixed memory size. The Array is an example.
• Dynamic Data Structures size can change dynamically at runtime. They are efficient
in memory as compared to the static data structure. Stack, Queue, and Linked list
are examples of dynamic data structures.
• The elements are present at the same level which allows traversing in a single run.
• The time complexity increase as data size increase.
• Work well mainly in the development of application software.
Linear Data Structures

• Arrange the elements in non-sequential order (a hierarchical order).
• The linear data structures are Trees, Graphs, Tables, Sets etc.
• The elements are present at various levels, so you can’t traverse them in a single run.
• Time complexity remains the same.
• Work well in image processing and Artificial Intelligence.
Non Linear Data Structures

• Language independent
• Improves logic building
• Improved problems solving approach
• Enables to solving real-world problems
• Helps in writing optimize code
• Improves adaptability to emerging tech stacks
• Helps to get jobs in top tech companies (MAANG)
DSA Advantages

• Insertion: Insert a new element to a data structure.
• Deletion: Delete an existing element from a data structure.
• Searching: Search an element inside a data structure.
• Sorting: Arranging the elements of a data structure in a specific order.
• Traversal: Visit each element inside a data structure exactly once.
• Merging: Combining two similar data structures together.
Common Data Structures Operations

• Abstract data types are data structures that define the declaration of Data and
Operations but not how these operations are implemented.
• The example of ADT are Array, Linked List, Stack, Queue, Binary Tree, Graphs etc.
• The implementation of ADT will be decided based on the programming language you
will use.
Abstract Data Types (ADTs)

• A step-by-step procedure to solve a given problem.
• There are two main criteria to judge an algorithm:
• There are two main criteria to analyze an algorithm:
• Effectiveness: How many steps it will take to give the desired result?
• Efficiency: How much time and memory it will take to execute?
• An algorithm which takes the minimum steps to produce the desired result is
considered the most effective.
• An algorithm which takes the minimum time and less space to execute is considered
the most efficient.
What is an Algorithm?

• Step 1: Start
• Step 2: Declare variables num1, num2 and sum.
• Step 3: Read the values of num1 and num2.
• Step 4: Add the value of num1 and num2 and assign the result to sum.
sum = num1+num2
• Step 5: Display the value of sum.
• Step 6: Stop
An Algorithm For Adding Two Numbers

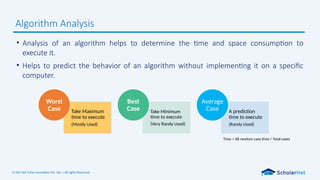
• Analysis of an algorithm helps to determine the time and space consumption to
execute it.
• Helps to predict the behavior of an algorithm without implementing it on a specific
computer.
Algorithm Analysis
Take Maximum
time to execute
(Mostly Used)
Worst
Case Take Minimum
time to execute
(Very Rarely Used)
Best
Case A prediction
time to execute
(Rarely Used)
Average
Case
Time = All random case time / Total cases

• Asymptotic analysis is a way of understanding how an algorithm behaves or performs
with the change in the input size.
• For example: In bubble sort, when the input array is in reverse order, the algorithm
takes the maximum time (quadratic) to sort the elements i.e. the worst case.
• But, when the input array is already sorted, the time taken by the algorithm is linear
i.e. the best case.
• When the input array is neither sorted nor in reverse order, then it takes average
time i.e. average case.
• These durations are denoted using asymptotic notations.
Asymptotic Analysis

• Big-O Notation (O-notation): Represents the upper bound of the running time of an
algorithm. It gives the worst-case complexity of an algorithm.
• Omega notation (Ω-notation): Represents the lower bound of the running time of an
algorithm. It provides the best-case complexity of an algorithm.
• Theta notation (Θ-notation): Represents the upper and the lower bound of the running
time of an algorithm. It is used for analyzing the average-case complexity of an
algorithm.
Asymptotic Notations

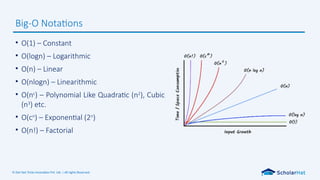
• O(1) – Constant
• O(logn) – Logarithmic
• O(n) – Linear
• O(nlogn) – Linearithmic
• O(nc
) – Polynomial Like Quadratic (n2
), Cubic
(n3
) etc.
• O(cn
) – Exponential (2n
)
• O(n!) – Factorial
Big-O Notations

• Always take the same amount of time to be executed
• Input size doesn’t matter, complexity remains the same.
• For example, accessing an element from an array at a given index. This will run only
once which is a constant.
O(1)- Constant Runtime Complexity
int[] numbers = new int[]
{10,20,30,40};
System.out.println(numbers[1]);

• Complexity goes up linearly while the input goes up exponentially.
• O(log n) notation is more scalable than O(n) and O(n²) as the input size grows larger
and larger.
• For example, Log to base 3
O(logn) – Logarithmic Runtime Complexity
int n=10;
for (int i = 1; i < n; i = i *
10){
System.out.println(i);
}

• The time to execute the algorithm is directly proportional to the input size n.
• Complexity grows linearly over time as the number of inputs increases i.e. Higher the
number of inputs, the higher the complexity.
• For example, Looping over all the items of an array.
O(n)- Linear Runtime Complexity
int[] numbers = new int[] {10,20,30,40};
for (int i=0; i< numbers.length; i++)
{
System.out.println(numbers[i]);
}

• The time to execute the algorithm will grow at a rate that is between linear and
exponential.
• Faster than linear but slower than exponential.
• For example: merge sort, quicksort and Heapsort.
O(nlogn) - Linearithmic Runtime Complexity
int n=10;
for (int i = 1; i <= n; i++){
for(int j = 1; j < n; j = j * 2) {
System.out.println( i + " " + j);
}
}

• The time to execute the algorithm is directly proportional to the power (c) of the input
size n.
• Like in Quadratic it is the square of input size n.
• For example, Iteration of Nested Loops.
O(nc
)- Polynomial Runtime Complexity
int n=10;
for (int i=0; i< n; i++)
{
for(int j=0; j<=i; j++)
{
System.out.println(n);
}
}

• The time to execute the algorithm becomes double with each addition to the input
dataset.
• These are often recursive algorithms that solve a problem of size n by recursively
solving two smaller problems of size n-1.
• For example, Generating a Fibonacci numbers using recursion.
O(cn
)- Exponential Runtime Complexity: O(2n
)
public int Fibonacci(int n){
if(n<=1){
return n;
}
else{
return Fibonacci(n-2) + Fibonacci(n-1);
}
}

• The runtime for calculating factorials grows exponentially with the number of inputs.
For example, 5! is 120, while 10! is 3628800.
• Grows pretty quickly, this algorithm has the worst time complexity.
• For example:
• Permutations of a string.
• Solving the travelling salesman problem with a brute-force search
O(n!)- Factorial Runtime Complexity
int n=10;
for (int i = 1; i <= factorial(n); i++)
{
System.out.println(i);
}

• In the case of multiple complexities take the worst case and that would be your
algorithm complexity.
• For example, o(n) + o(n2
) == o(n2
)
Multiple Runtime Complexity

• Constant O(1) – Accessing an element in an Array by index number.
• Linear O(n) – Linear Search.
• Logarithmic O(logn) – Binary Search.
• Linearithmic O(nlogn) – Heap Sort, Merge Sort.
• Polynomial O(n^c) – Bubble Sort, Selection Sort, Insertion Sort, Bucket Sort.
• Exponential O(c^n) – Tower of Hanoi.
• Factorial O(n!) – Permutations of a string, Brute force Search algorithm for Traveling
Salesman Problem.
Big-O Notation Algorithms Examples

• Single and Nested Loops
• Decrease and Conquer, Divide and Conquer, Transform and Conquer
• Binary Search
• Two Pointers and Sliding Window
• Breath First Search and Depth First Search
• Data Structures: Stack, Queue, Hash Table, Trie, Heap, BST etc.
• Dynamic Programming
• Greedy Algorithms
Problem Solving Techniques

DSA_Big_O_ Data_Structure_and_Algorithm.pptx

More Related Content

Similar to DSA_Big_O_ Data_Structure_and_Algorithm.pptx

Recently uploaded

DSA_Big_O_ Data_Structure_and_Algorithm.pptx

Editor's Notes