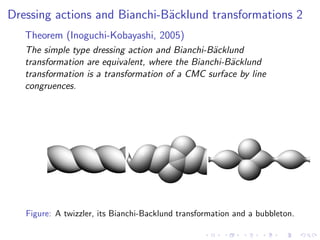
This document discusses dressing actions on integrable surfaces. Specifically, it examines: 1) Dressing actions and their relationship to Bianchi-Bäcklund transformations for constant negative Gauss curvature surfaces. 2) Extending these ideas to complex constant mean curvature surfaces and real forms through double loop group decompositions and dressing actions on complex extended frames. 3) How these techniques can be used to classify different classes of integrable surfaces.

1. Dressing actions on integrable surfaces
This is a joint work with Nick Schmitt at T¨bingen University.
u
Shimpei Kobayashi, Hirosaki University
6/21, 2011

2. Introduction
Overview
(Bianchi) B¨cklund transformation
a
Harmonic maps into symmetric spaces
Loop groups
Dressing actions and Bianchi-B¨cklund transformations
a
Factorizations and dressing actions
Dressing actions and Bianchi-B¨cklund transformations
a
Complex CMC surfaces and real forms
Complex CMC surfaces
Real forms
Integrable surfaces
Dressing action on complex extended frames
Double loop group decomposition
Dressing action on complex extended frames
Dressing action on integrable surfaces

3. Overview1: Motivation
◮ Understand transformation theory of surfaces in terms of
modern language; flat connections, harmonic maps and loop
groups.
◮ More specifically: Why do constant positive Gauss curvature
surfaces have only Bianchi-B¨cklund transformation? Note!
a
Constant negative Gauss curvature surfaces have also
B¨cklund transformation.
a
Remark
◮ B¨cklund transformation is a transformation by tangential line
a
congruences and Bianchi-B¨cklund transformation is an
a
extension of the B¨cklund transformation by Bianchi.
a
◮ Classical theorem by B¨cklund says that if two surfaces are
a
related by B¨cklund transformation, then they are constant
a
negative Gauss curvature surfaces.

4. Overview 2: Previous works
Remark
◮ Uhlenbeck considered dressing action on extended frame of
harmonic maps into Lie groups, J. Diff. Geom. 1989.
◮ Uhlenbeck proved that the simple factor dressing action on
extended frames of negative CGC surfaces is equivalent to the
B¨cklund transformation, J. Geom. Phys. 1992.
a
◮ Terng and Uhlenbeck generalized the dressing action to
U/K-system, Comm. Pure Appl. Math. 2000.

5. B¨cklund transformation
a
Theorem (Backlund)
S, S ′ ⊂ R3 : a surface in Euclidean three space
S and S ′ are related by the tangential line congruences with
constant angle and distance.
⇓
S and S ′ are constant negative Gauss curvature surfaces.
Remark
◮ Tangential line congruences ℓ are line congruences which
tangent to both surfaces.
◮ ˜
Angle between S and S ′ are determined by N, N = c,
˜
where N and N are the unit normal fields of S and S ′ .

6. Bianchi-B¨cklund transformation
a
Theorem (Bianchi)
Let S ⊂ R3 be a CGC surface. There exits a surface S ′ in
complex Euclidean three space such that S and S ′ are related by
tangential line congruences with complex constant angle. This
transformation is called a Bianchi-B¨cklund transformation.
a
Moreover, twice of the Bianchi-B¨cklund transformation with
a
suitable angle conditions gives a CGC surface in R3

7. Permutability and superposition formula
∗
β,β = S β ∗ ,β
Sκ κ .
β
θ β∗
u u
ˆ
β∗ β
θ∗
The superposition formula:
u−u
ˆ β − β∗ θβ − θβ∗
tanh = tanh tanh ,
2 2 2
ˆ ˆ
where u = θβ,β∗ = θβ∗ ,β .
ˆ

8. A family of flat connections
Theorem (Pohlmeyer 1976)
Let M be a simply connected open Riemann surface and G/K a
symmetric space. The followings are equivalent.
1. Φ : M → G/K is a harmonic map.
2. There exist a Fλ : M → ΛGσ such that
F−1 dFλ = λ−1 α′ + αk + λα′′ and π ◦ F|λ=1 = Φ.
λ p p
Corollary
The set of extended frames, Fλ.
The family of CMC surfaces, fλ.

9. Loop groups
ΛGC := {H : S1 → GC | σH(λ) = H(−λ)},
σ
ΛGσ := {H ∈ ΛGC | H(λ) = H(λ) on λ ∈ S1 },
σ
H± can be extend holomorphically
Λ±GC :=
σ H± ∈ ΛGC |
σ ,
to D (or E).
Λ±GC := H± ∈ Λ±GC | H+ (0) = id (or H−(∞) = id) ,
∗ σ σ
ΛgC := {h : S1 → gC | σh(λ) = h(−λ)}.
σ

10. Loop groups
ΛGC := {H : S1 → GC | σH(λ) = H(−λ)},
σ
ΛGσ := {H ∈ ΛGC | H(λ) = H(λ) on λ ∈ S1 },
σ
H± can be extend holomorphically
Λ±GC :=
σ H± ∈ ΛGC |
σ ,
to D (or E).
Λ±GC := H± ∈ Λ±GC | H+ (0) = id (or H−(∞) = id) ,
∗ σ σ
ΛgC := {h : S1 → gC | σh(λ) = h(−λ)}.
σ
Fourier expansions of H ∈ ΛGσ and H± ∈ Λ±GC :
σ
H = · · · + λ−2 H−2 + λ−1 H−1 + H0 + λH1 + λ2 H2 + · · · ,
H± = H±,0 + λ±1 H±,1 + λ±2 H±,2 + · · · ,
where Hj = H−j , σHj = (−1)j Hj , and σH±,j = (−1)j H±,j .

11. Loop groups factorizations
Theorem (Birkhoff and Iwasawa decompositions)
1. Birkhoff decomposition:
Λ+ GC × Λ−GC → ΛGC
∗ σ σ σ
is a diffeomorphism onto the open dense subset
Λ+ GC · Λ−GC of ΛGC .
∗ σ σ σ
2. Iwasawa decomposition: Assume that G is compact.
ΛGσ × Λ−GC → ΛGC
σ σ
C
is a diffeomorphism onto ΛGσ .
Remark
The Iwasawa decomposition is obtained from the Birkhoff
decomposition and a real from.

12. Dressing actions and Bianchi-B¨cklund transformations 1
a
Let F be an extended framing and g an element in Λ+ GC .
σ
Decompose gF according to the Iwasawa decomposition as
˜
ΛGC ∋ gF = FV+ ∈ ΛGσ × Λ+ GC .
σ σ
Then
˜
◮ F is again the extended framing. Thus Λ+ GC acts, the
σ
dressing action, that is, Id#F = F and
˜ −1
g(#(f#F)) = (gf)#F, where g#F = F = gFV+ .
◮ Bianchi permutability theorem is just associativity of the
action:
g2 #(g1 #F) = g2 #(ˆ1 #F),
ˆ g
where g2 g1 = ˆ2 g1 .
g ˆ
◮ The dressing action by rational loops with simple pole is called
the simple type dressing action.

13. Dressing actions and Bianchi-B¨cklund transformations 2
a
Theorem (Inoguchi-Kobayashi, 2005)
The simple type dressing action and Bianchi-B¨cklund
a
transformation are equivalent, where the Bianchi-B¨cklund
a
transformation is a transformation of a CMC surface by line
congruences.
Figure: A twizzler, its Bianchi-Backlund transformation and a bubbleton.

14. Recall that a simple factor dressing by g:
−1
g#F = gFV+ .
This action corresponds to the twice of Bianchi-B¨cklund
a
transformation.
The g has two simple poles at λ1 , λ2 , which are related
¯
λ2 = 1/λ1 ∈ C× S1 .
◮ Is is possible to factor g to
g = g2 g1
so that each gj corresponds to once Bianchi-B¨cklund?
a
◮ Answer: Yes, but one needs an extension of the dressing
action.

15. Constant negative Gauss curvature surfaces
Fact
There exists a similar dressing action on constant negative Gauss
curvature surfaces. Try to unify negative and positive Gauss
curvature surfaces.
⇓
◮ Complex CMC surfaces (Dorfmeister-Kobayashi-Pedit 2010).
◮ Real form surfaces (Kobayashi 2011).

16. Ruh-Vilms type theorem
Theorem
The following two conditions are equivalent:
1. The complex mean curvature H is constant.
2. There exist a Fλ : D2 → ΛGσ (= ΛSL2 Cσ ) such that
C
F−1 dFλ = λ−1 α′ + αk + λα′′ and π ◦ F|λ=1 = Φ, where
λ p p
Φ is the unit normal to f. Here ′ (resp. ′′) denotes dz-part
and (resp. dw-part).
◮ Fλ (F in short) is called the complex extended framing.
◮ The complex CMC surfaces are given by Sym formula for F.

17. Almost compact real forms
Theorem (Kobayashi, 2011)
Let cj for j ∈ {1, 2, 3, 4} be the following involutions on Λsl2 Cσ :
t
¯
c1 : g(λ) → −g(−1/λ) , ¯
c2 : g(λ) → g −1/λ ,
t √ t
¯ 1/ i 0 ¯
c3 : g(λ) → −g 1/λ , c4 : g(λ) → −Ad √ g(i/λ) ,
0 i
where g ∈ Λsl2 Cσ . Then, the almost compact real forms of
Λsl2 Cσ are the following real Lie subalgebras of Λsl2 Cσ :
Λsl2 C(c,j) = {g ∈ Λsl2 Cσ | cj ◦ g(λ) = g(λ) } .
σ

18. Almost split real forms
Theorem (Kobayashi, 2011)
Let sj for j ∈ {1, 2, 3} be the following involutions on Λsl2 Cσ :
t
¯
s1 : g(λ) → −g(−λ) , ¯
s2 : g(λ) → g −λ ,
t
s3 : g(λ) → −Ad λ 0 ¯
g λ ,
0 λ−1
where g ∈ Λsl2 Cσ . Then, the almost split real forms of Λsl2 Cσ
are the following real Lie subalgebras of Λsl2 Cσ :
Λsl2 C(s,j) = {g ∈ Λsl2 Cσ | sj ◦ g(λ) = g(λ) } .
σ

19. Integrable surfaces
Theorem (Kobayashi, 2011)
The real forms induce the following integrable surfaces.
Surfaces class Gauß curvature Gauß curvature : Parallel CMC
R3 K(s,3) = −4|H|2 K(c,3) = 4|H|2 : H(c,3) = |H|
Spacelike R1,2 K(s,1) = 4|H|2 K(c,1) = −4|H|2 : H(c,1) = |H|
Timelike R1,2 K(c,2) = −4|H|2 K(s,2) = 4|H|2 : H(s,2) = |H|
H3 * : H(c,4) = tanh(q)

20. Double loop group decomposition
The following r-loop group and its loop subgroups will be used.
Hr,R = Λr SL2 C × ΛR SL2 C,
H+ = Λ+ SL2 C × Λ−SL2 C ⊂ Hr,R ,
r,R r R
g1 and g2 extends holomorphically
H− = (g1 , g2 ) ∈ Hr,R .
r,R to Ar,R and g1 |Ar,R = g2 |Ar,R

21. Theorem
The multiplication map
H− × H+ → H
is a diffeomorphism on an open dense subset of H, which is called
the big cell. On the big cell, an element (gr , gR ) ∈ H can be
decomposed as
(gr , gR ) = (F, F)(h+ , h−),
r R
where (F, F) ∈ H− denotes the boundary values on Cr and CR of
the map F : Ar,R → ΛSL2 Cσ and (hr , h−) is an element in H+ .
+
R

22. Dressing action on complex extended frames
Let F be a diagonal set of complex extended frames:
F = {(F, F) | F is a complex extended frames.}
Then H acts F as follows:
˜ ˜
Let (gr , gR ) ∈ H and (F, F) ∈ F. Define (F, F)
˜ ˜
(F, F) = (gr F, gR F)Ar,R ,
where the subscript Ar,R denotes the H− part of the double loop
˜ ˜
group decomposition. Denote (F, F) by
˜ ˜
(F, F) = (gr , gR )#(F, F).
It is easy to see that (Id, Id)#(F, F) = (F, F) and
(˜r , gR )#((gr , gR )#(F, F)) = ((˜r , gR ) · (gr , gR ))#(F, F).
g ˜ g ˜

23. ρ dressing action on complex extended frames
We generalized H to K as
˜
K = {(gr , gR ) | gr ∈ Λr SL2 C and gR ∈ ΛR SL2 C.}.
Let (gr , gR ) ∈ K and
√
0 λ
ρ= √ −1 .
− λ 0
˜ ˜
Define (F, F) by
˜ ˜
(F, F) = (gr F, gR Fρj )Ar,R ,
where j = 4 if gR is single valued and j = 1 if gR is double valued.
˜ ˜
part of the double loop group decomposition. Denote (F, F) by
˜ ˜
(F, F) = (gr , gR )#ρ(F, F).

24. Theorem (Kobayashi-Schmitt)
1. #ρ defines an action and it is an extension of the dressing
action.
2. If F and g satisfy CMC (positive CGC) reality condition, then
the dressing action reduces to the CMC dressing action.
3. If F and g satisfy negative CGC reality condition, then the
dressing action reduces to the negative CGC dressing action.
Remark
◮ ¯
The CMC case, the simple poles must be pair λ1 , 1/λ1 . Thus
Bianchi-B¨cklund transformation can only be applied.
a
◮ The CMC case, the simple poles need not to be pair. Thus
B¨cklund and Bianchi-B¨cklund transformation can be
a a
applied.