DOMINIO DE UNA FUNCION

1. DOMINIO DE UNA FUNCION
Determina el dominio y el recorrido de estas funciones en R
a). 𝒈( 𝒙) =
𝒙
𝒙−𝟏
𝑥 − 1 ≠ 0
𝑥 ≠ 1
Dominio: R – {1}
𝑔( 𝑥) = 𝑦 =
𝑥
𝑥 − 1
𝑦(𝑥 − 1) = 𝑥
𝑥𝑦 − 𝑦 = 𝑥
𝑥𝑦 − 𝑥 = 𝑦
𝑥( 𝑦 − 1) = 𝑦
𝑥 =
𝑦
𝑦 − 1
𝑦 − 1 ≠ 0 → 𝑦 ≠ 1
𝑦 ≠ 1
Recorrido:R – {1}
b). 𝒇( 𝒙) =
𝟐𝒙
𝒙+𝟑
𝑥 + 3 ≠ 0
𝑥 ≠ −3
Dominio: R – {-3}
𝑓( 𝑥) = 𝑦 =
2𝑥
𝑥 + 3
𝑦( 𝑥 + 3) = 2𝑥
𝑥𝑦 + 3𝑦 = 2𝑥
𝑥𝑦 − 2𝑥 = −3𝑦
𝑥( 𝑦 − 2) = −3𝑦
𝑥 =
−3𝑦
𝑦 − 2
𝑦 − 2 ≠ 0 → 𝑦 ≠ 2
Rango: R – {2}

2. DOMINIO DE UNA FUNCION
c). 𝒇( 𝒙) = √𝟏 − 𝒙 𝟐
1 − 𝑥2
≥ 0
(1 − 𝑥)(1+ 𝑥) ≥ 0
1 − 𝑥 ≥ 0 1+ 𝑥 ≥ 0
−𝑥 ≥ −1 𝑥 ≥ −1
𝑥 ≤ 1
Dominio: [-1, 1]
𝑓( 𝑥) = 𝑦 = √1 − 𝑥2
𝑦2
= 1 − 𝑥2
𝑥2
= 1 − 𝑦2
𝑥 = √1 − 𝑦2
1 − 𝑦2
≥ 0
(1 − 𝑦)(1+ 𝑦) ≥ 0
1 − 𝑦 ≥ 0 1+ 𝑦 ≥ 0
−𝑦 ≥ −1 𝑦 ≥ −1
𝑦 ≤ 1
Rango: [0,1)
d). 𝒓( 𝒙) = √ 𝒙 𝟐 − 𝟏
𝑥2
− 1 ≥ 0
(𝑥 − 1)(𝑥 + 1) ≥ 0
𝑥 − 1 ≥ 0 𝑥 + 1 ≥ 0
𝑥 ≥ 1 𝑥 ≥ −1
Dominio: [1, ∞+)
𝑟( 𝑥) = 𝑦 = √ 𝑥2 − 1
𝑦2
= 𝑥2
− 1
𝑦2
+ 1 = 𝑥2

3. DOMINIO DE UNA FUNCION
𝑥 = √ 𝑦2 − 1
𝑦2
− 1 ≥ 0
(𝑦 − 1)(𝑦 + 1) ≥ 0
𝑦 − 1 ≥ 0 𝑦 + 1 ≥ 0
𝑦 ≥ 1 𝑦 ≥ −1
Dominio: [0, ∞+)
e). 𝒈( 𝒙) =
𝟐
√| 𝒙−𝟐|−𝟏
| 𝑥 − 2| − 1 ≥ 0
| 𝑥 − 2| ≥ 1
𝑥 − 2 ≥ 1 𝑥 − 2 ≤ −1
𝑥 ≥ 3 𝑥 ≤ 1
Dominio: (∞-,1]U[3,∞+)
f). 𝒇( 𝒙) =
𝒙 𝟐−𝟏
𝒙 𝟐+𝟏
𝑥2
+ 1 ≠ 0
𝑥2
≠ −1
𝑥 = √−1 No existe
Dominio: R

4. DOMINIO DE UNA FUNCION
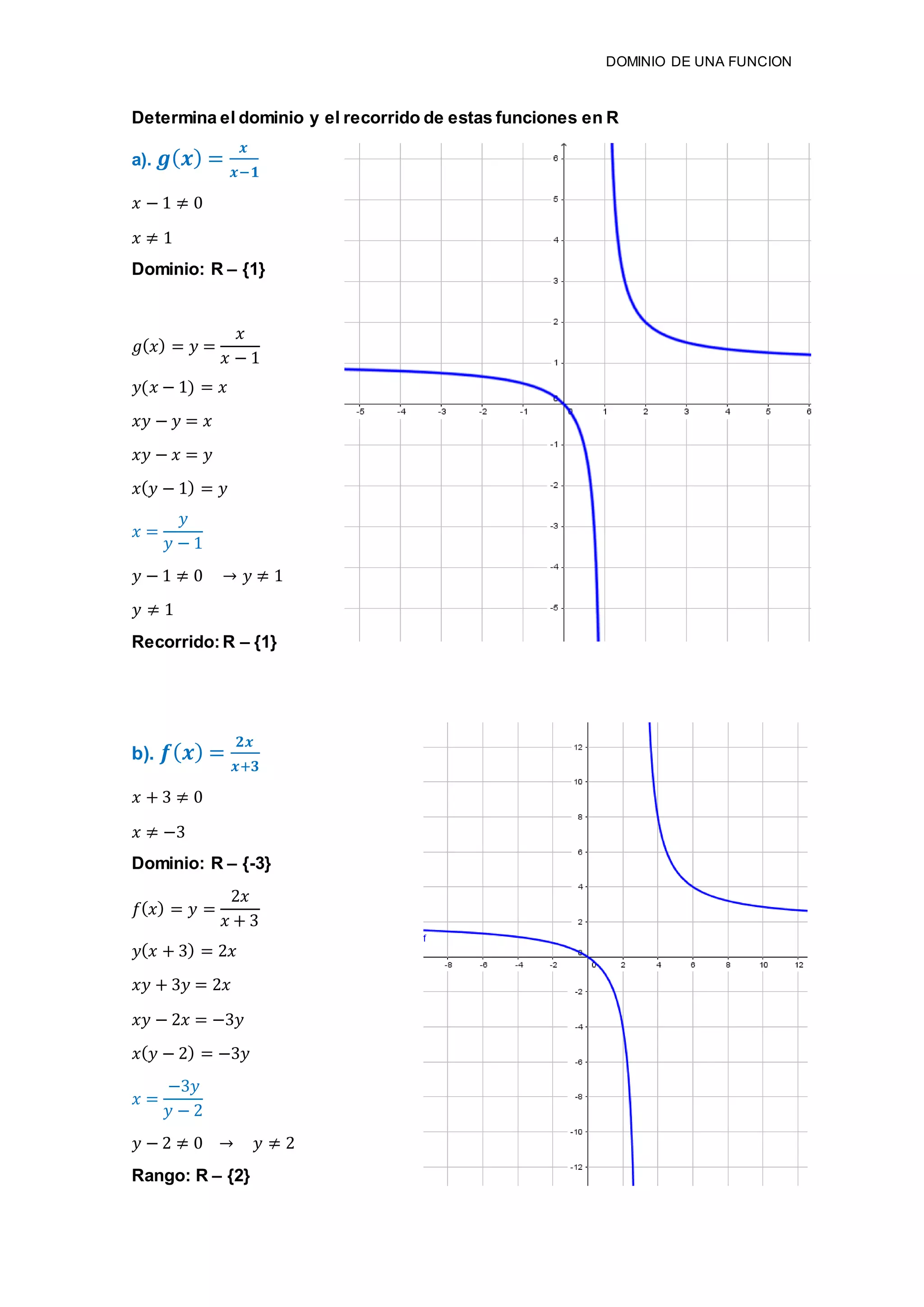
g). 𝒇( 𝒙) =
𝟏
𝒙−𝟏
+
𝟏
𝒙−𝟐
𝑥 − 1 ≠ 0 𝑥 − 2 ≠ 0
𝑥 ≠ 1 𝑥 ≠ 2
Dominio: R – {1,2}
h). 𝒉( 𝒙) = √ 𝒙 − 𝟏 + √ 𝒙 − 𝟐
𝑥 − 1 ≥ 0 𝑥 − 2 ≥ 0
𝑥 ≥ 1 𝑥 ≥ 2
Dominio: [2, ∞+)