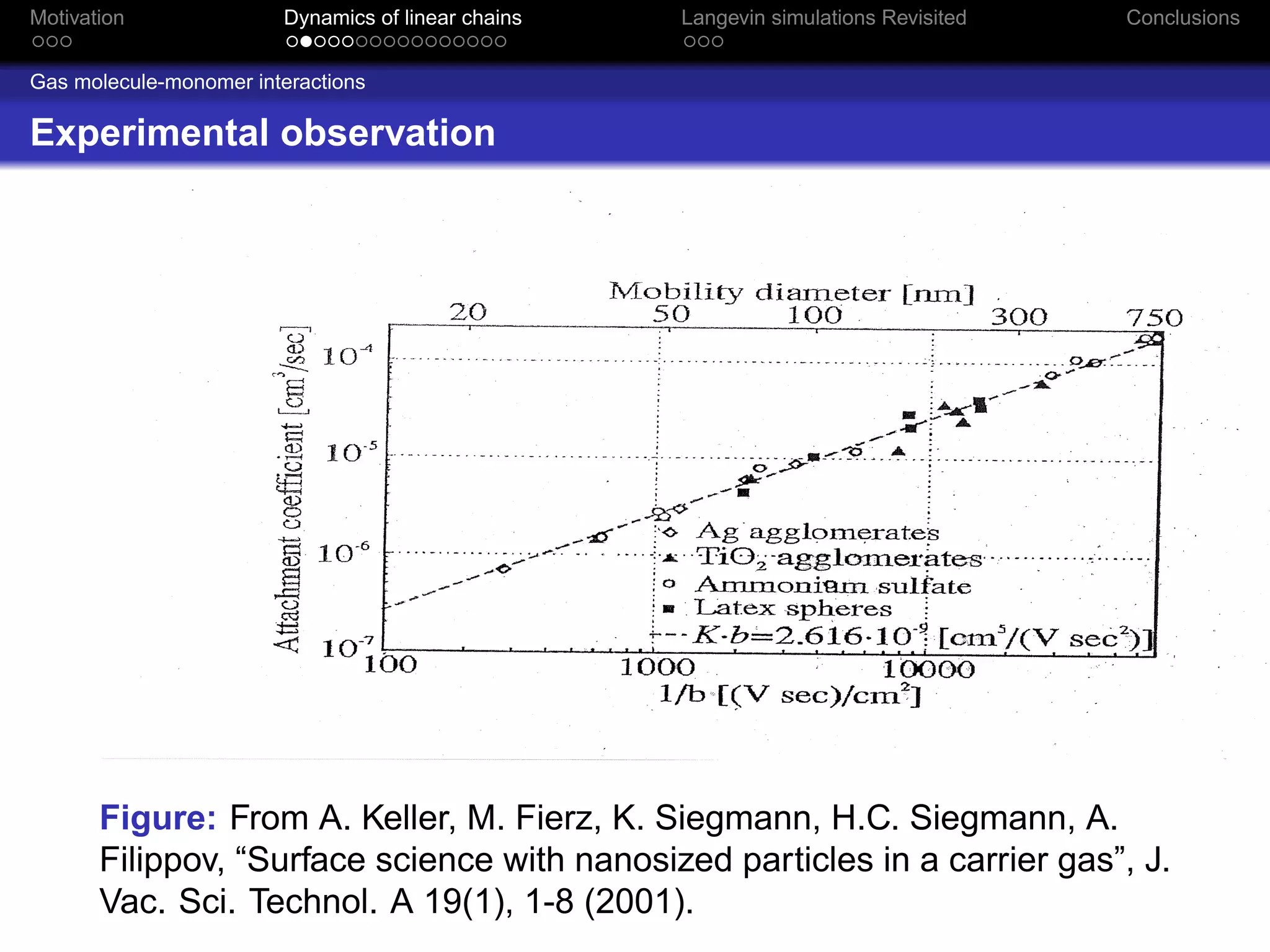
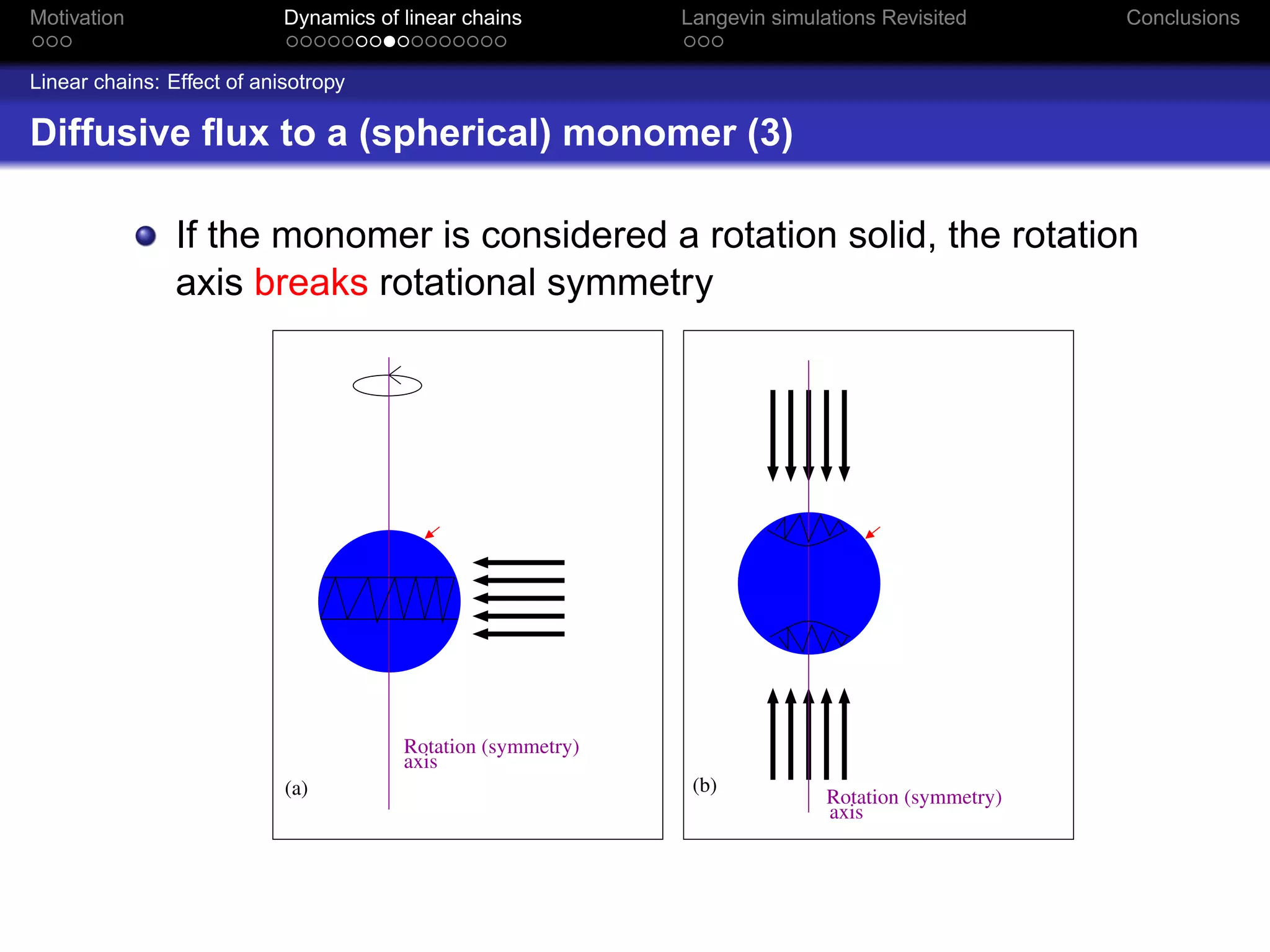
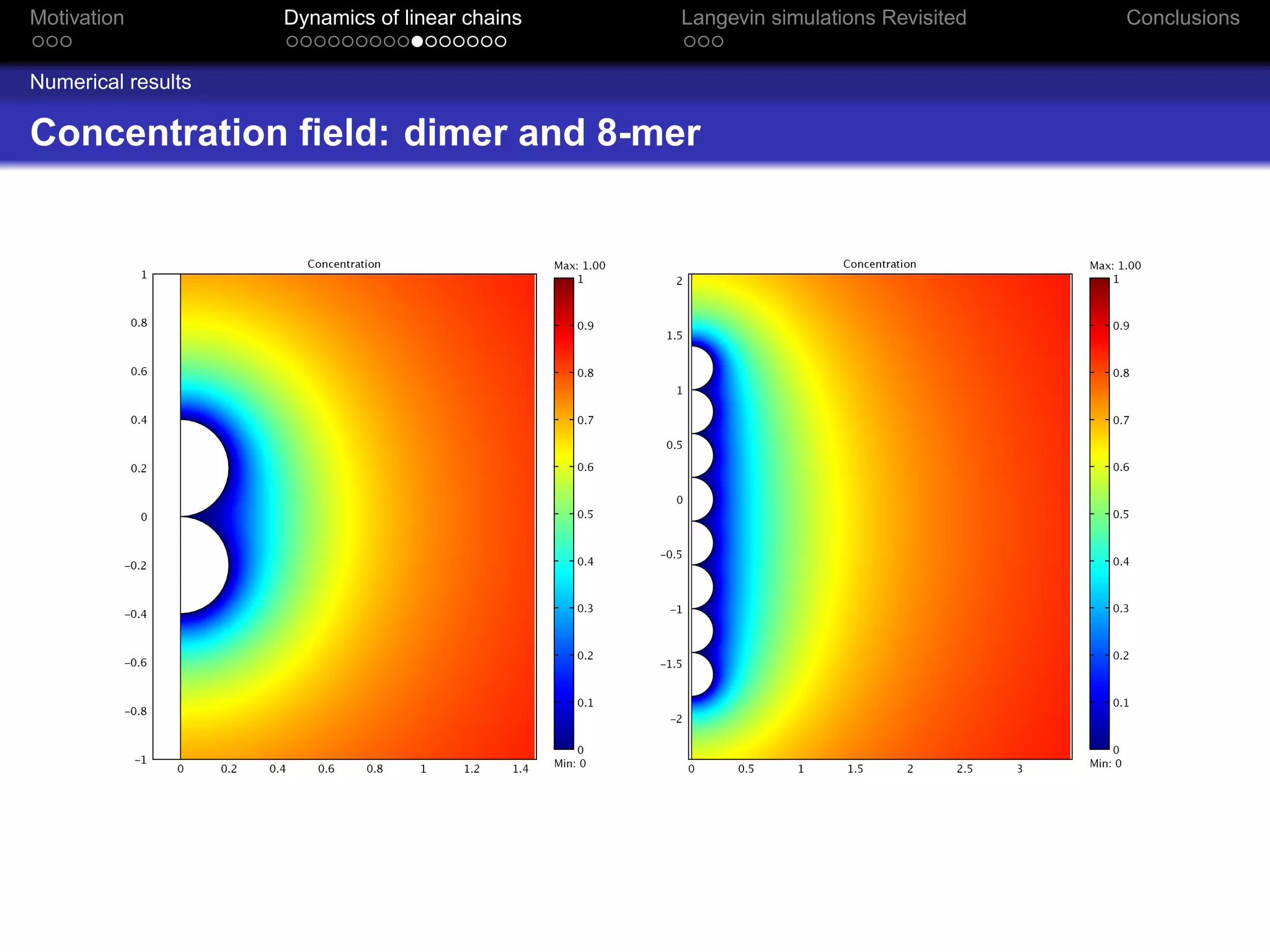
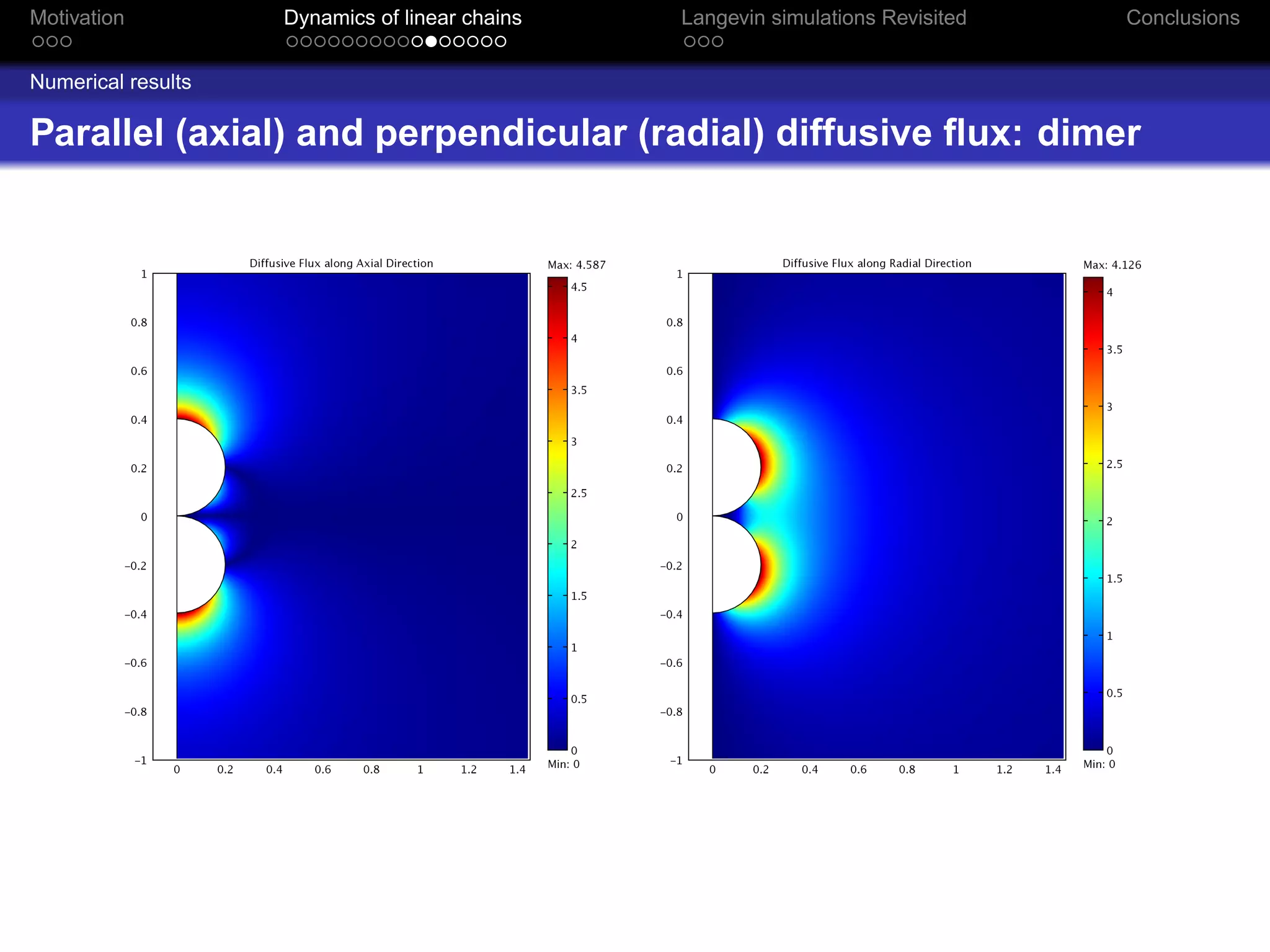
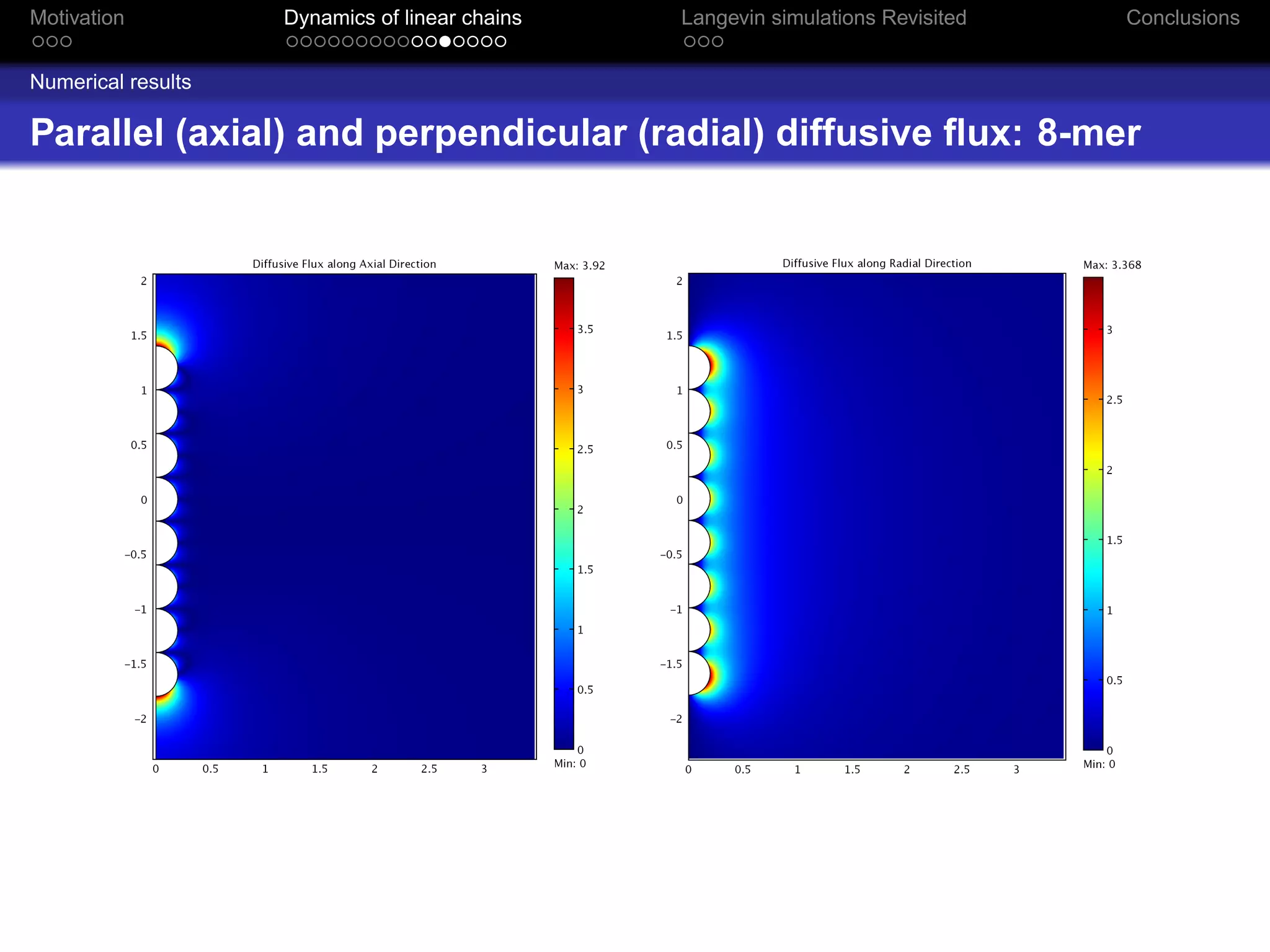
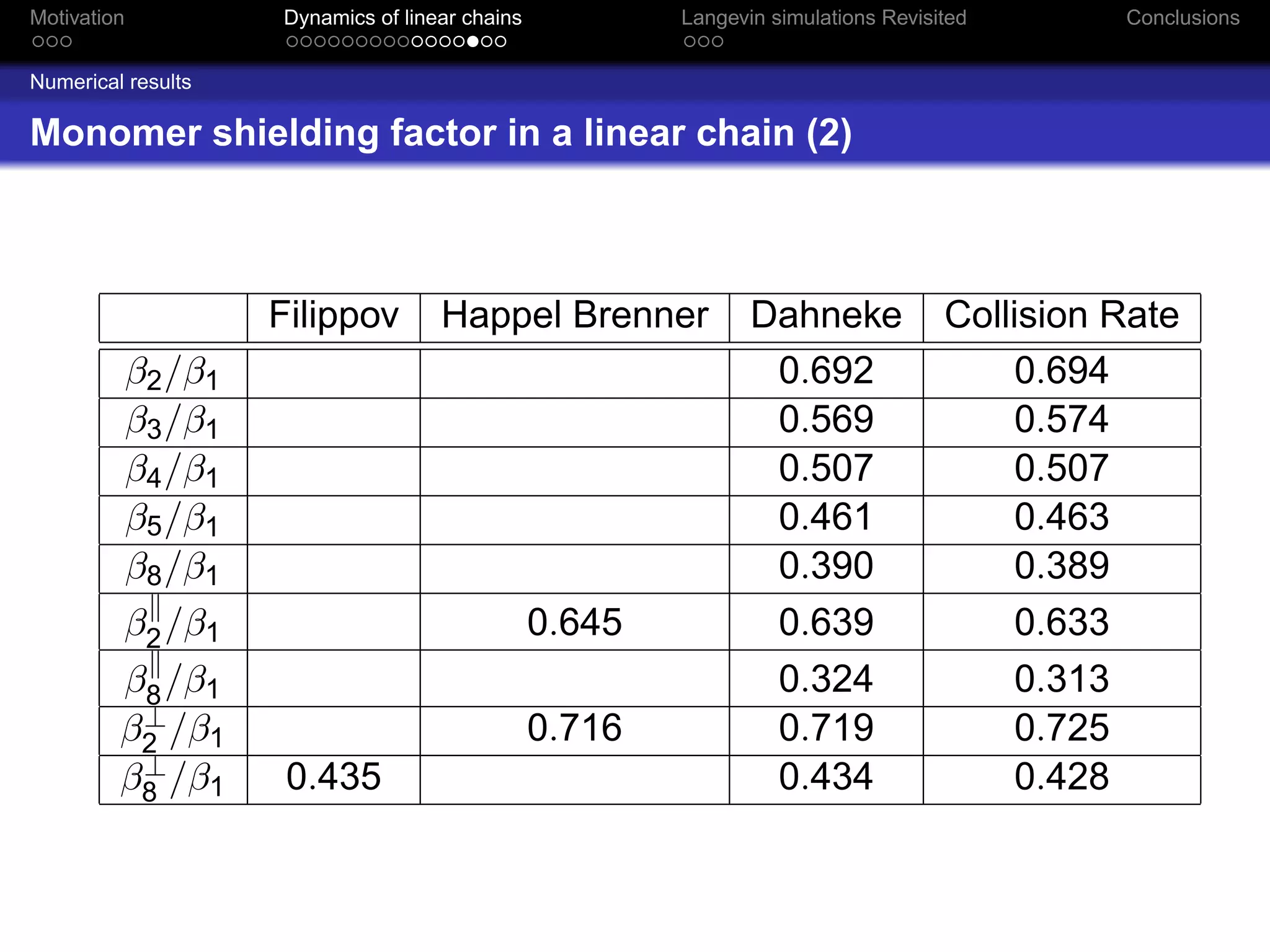
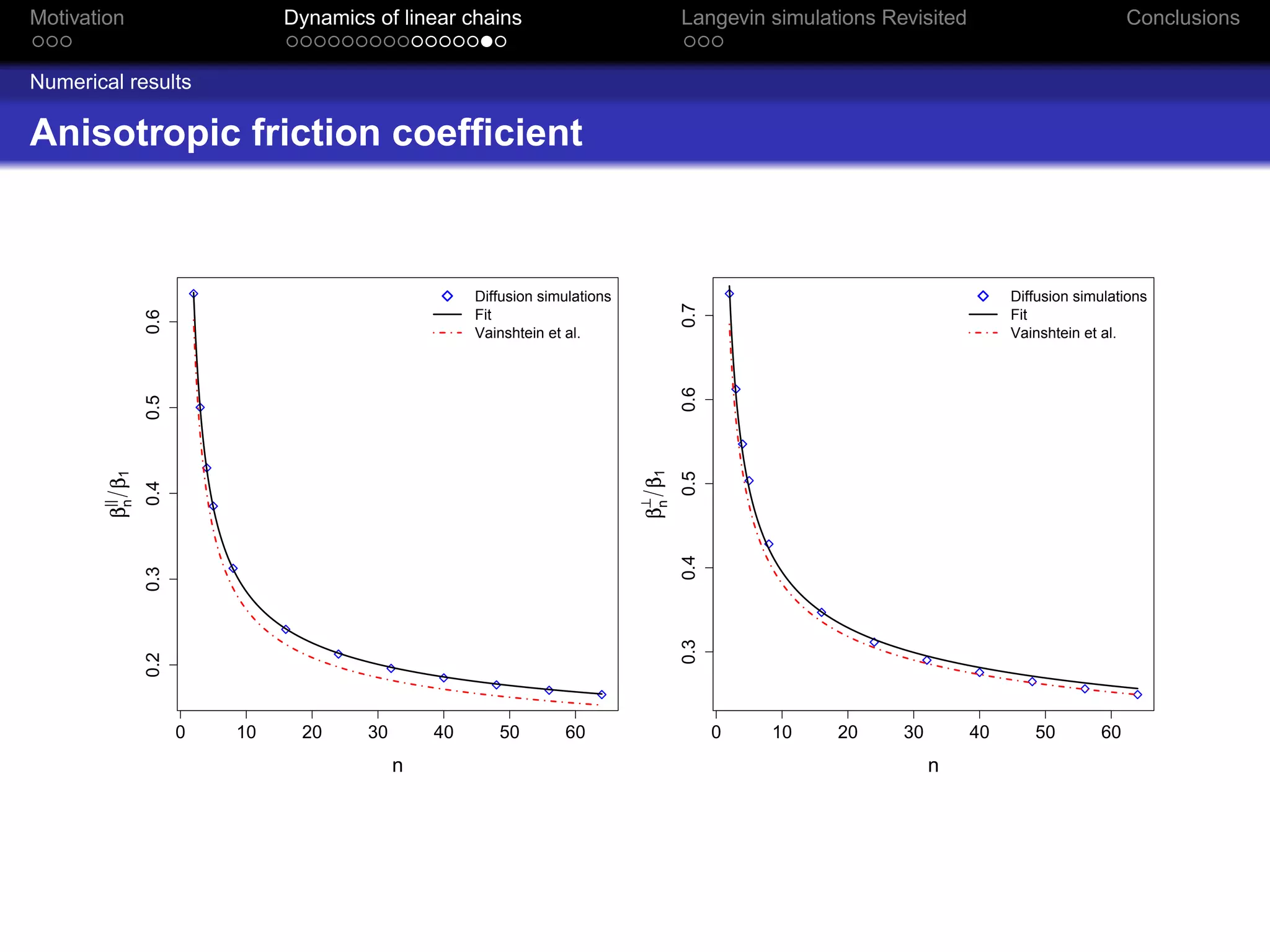
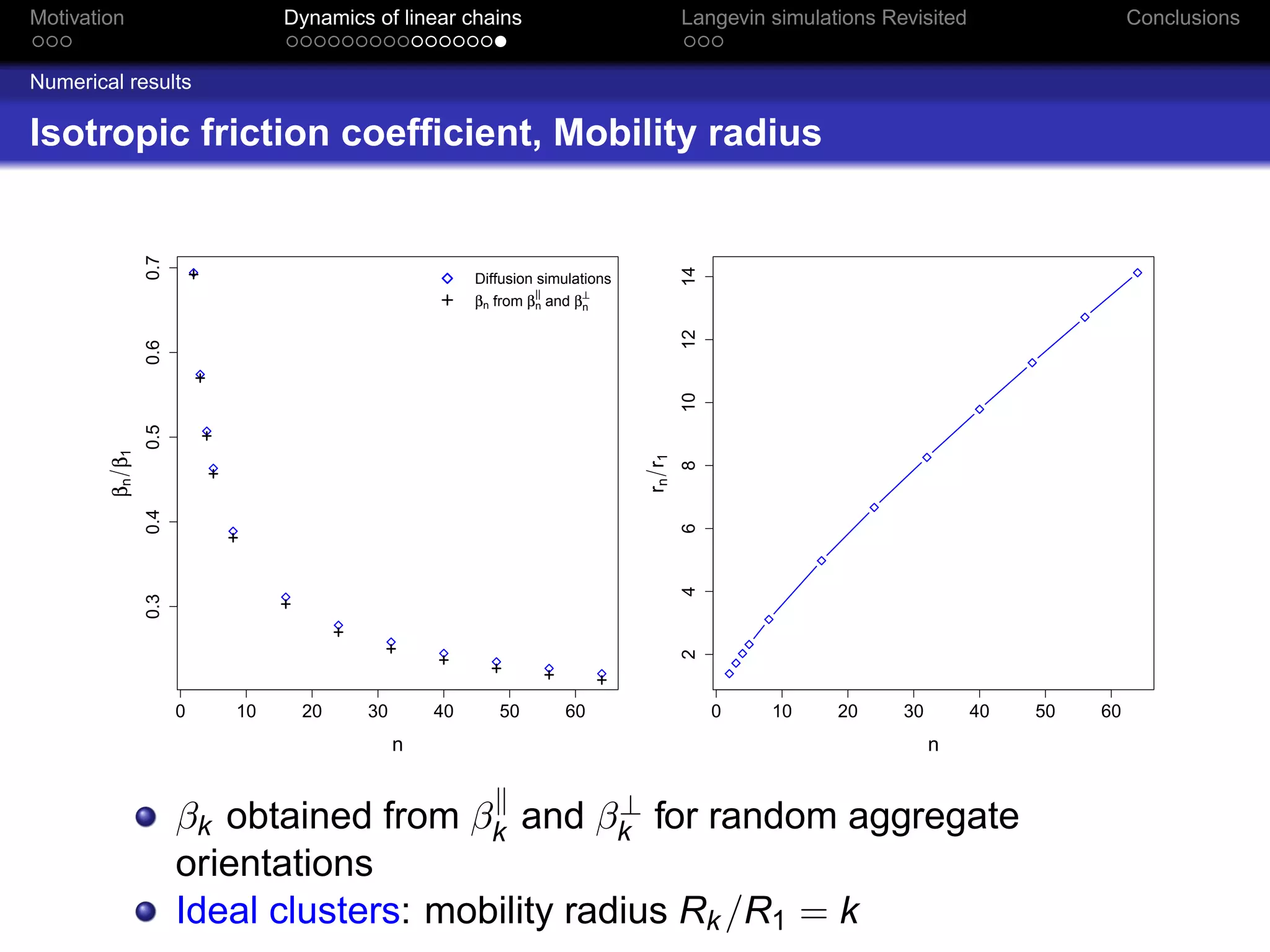
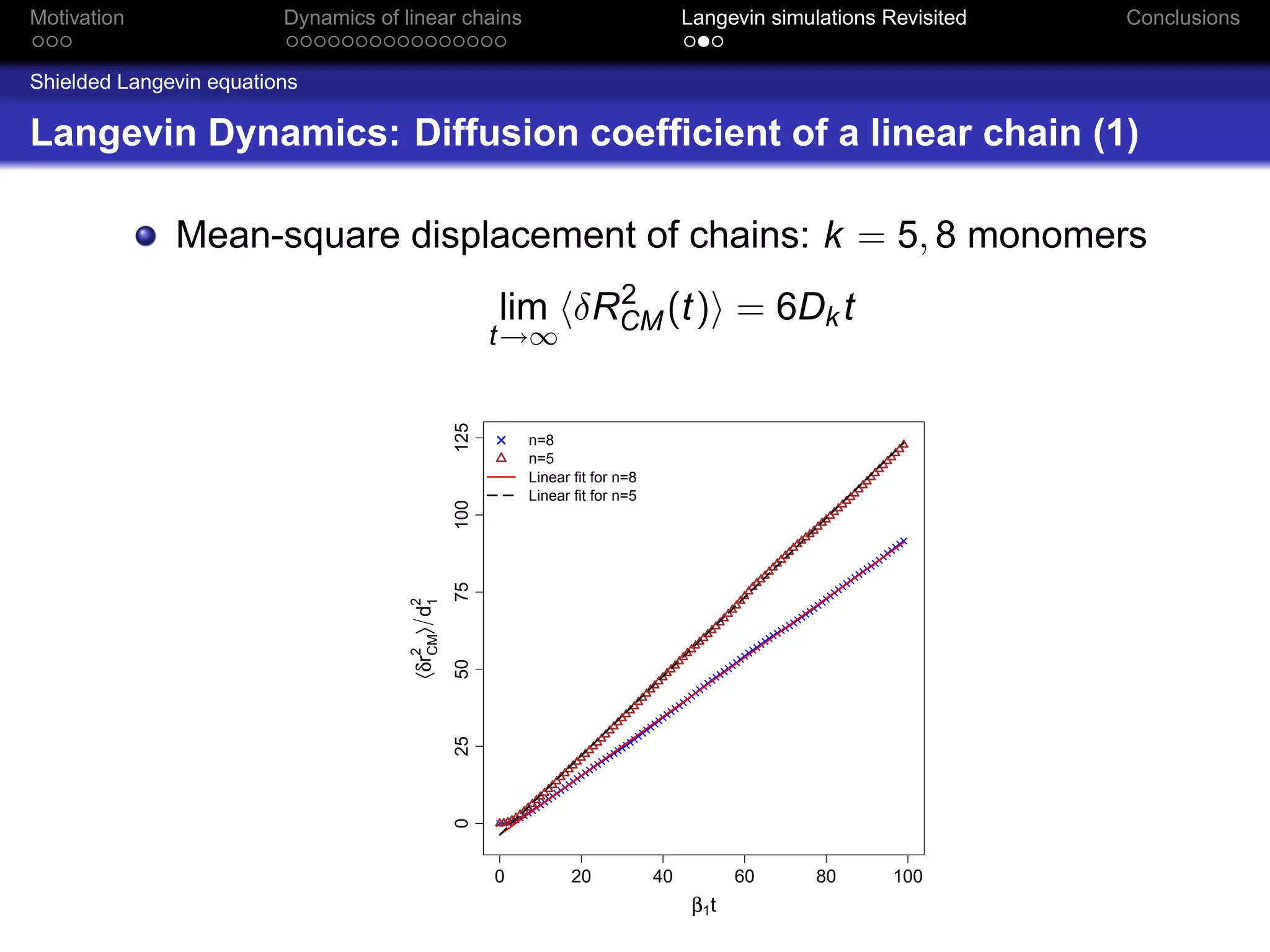
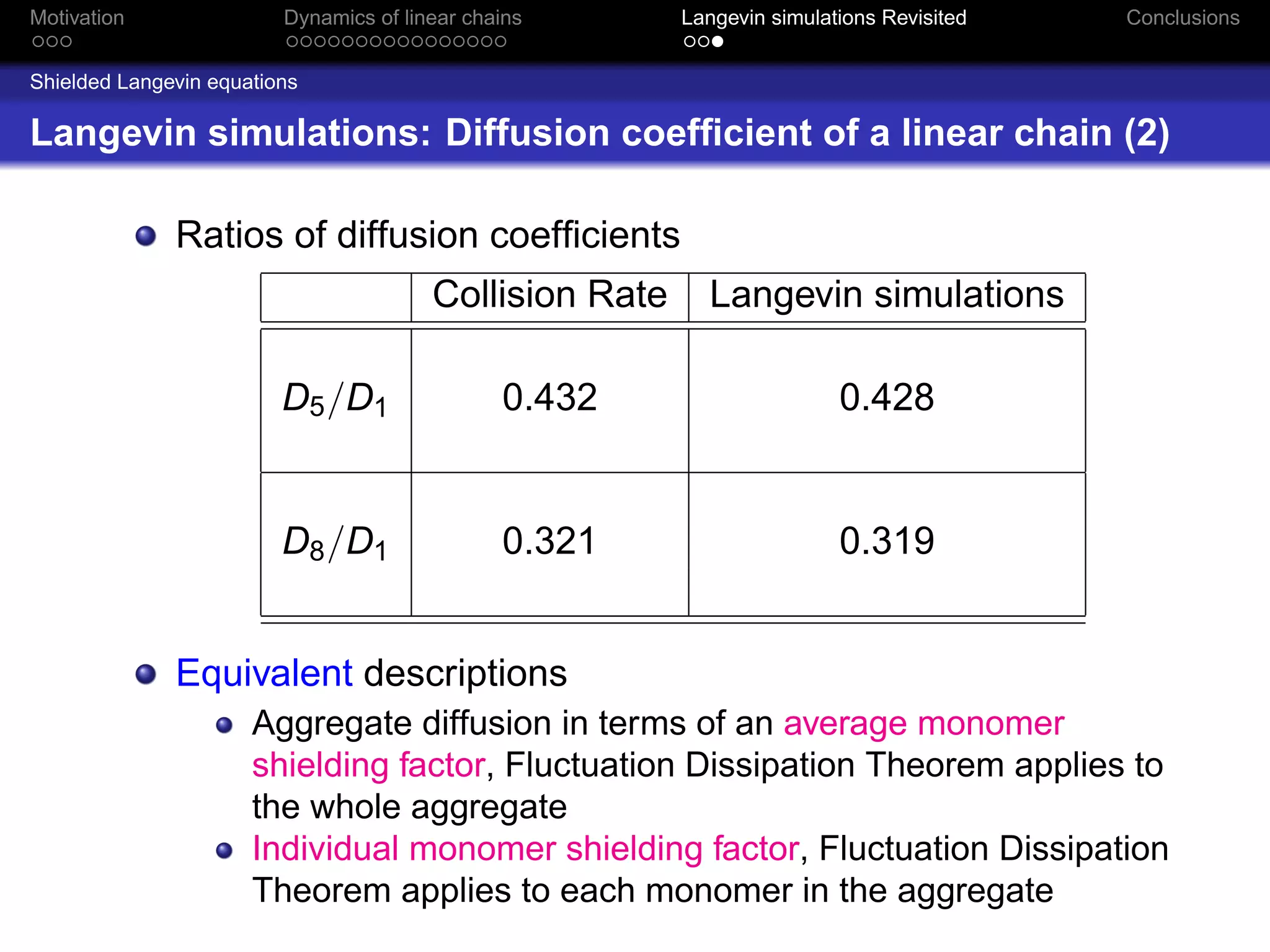
The document revisits the dynamics of linear chains in Langevin simulations, focusing on the calculation of friction coefficients for monomers in aggregates. It discusses the active surface concept and its impact on diffusion and friction coefficients, emphasizing the relationship between molecular collision rates and the performance of aggregates. The findings suggest that the shielding factor of monomers is significant, providing insights that align with previous theoretical models while acknowledging limitations in momentum transfer treatment.

1. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Diffusion coefficient of linear chains
Is active surface a useful concept?
Lorenzo Isella Yannis Drossinos
European Commission
Joint Research Centre
Ispra (VA), Italy
European Aerosol Conference 2009, Karlsruhe

2. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Objectives
Physical system
Fractal aggregate (e.g., soot particle) composed of k
(spherical) monomers
Brownian motion in a quiescent fluid
Continuum regime
Motivation
Monomers in an aggregate are shielded
Langevin simulation with unshielded monomers generate
ideal clusters
Aim
to determine an algorithm for the calculation of the friction
coefficient of a monomer of a k -monomer aggregates
to use it in Langevin simulations of aggregate formation in
terms of monomer properties

3. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Friction coefficient of a k -aggregate
Aggregate equation of motion
dvk
mk = −fk vk + F(t)
dt
Stokes drag force arises from collisions with carrier-gas
molecules
Aggregate friction coefficient fk = k m1 βk
βk average friction coefficient per monomer (unit mass)
Random force models fluctuating force resulting from
thermal motion of carrier gas molecules
Stokes drag and friction coefficient similar origin:
Fluctuation Dissipation Theorem relates them

4. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Shielding factor
Average monomer shielding factor ηk in a k -aggregate
fk km1 βk βk
= = ≡ ηk
kf1 km1 β1 β1
Stokes-Einstein diffusion coefficient
kB T 1
Dk = = D1
km1 βk k ηk
Mobility radius Rk defined through Dk ≡ kB T /(6πµRk )
Rk
= k ηk
R1
Ideal clusters: ηk = 1

5. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Gas molecule-monomer interactions
Active surface
Description of (carrier gas) molecule-monomer interactions
in term of Active Surface (or Fuchs surface)
Fraction of geometrical surface area directly accessible
(exposed) to gas molecules
Active surface determines condensational growth,
adsorption kinetics
Surface area active in mass and momentum transfer
Experimentally measurable: attachment rate of diffusing
ions (diffusion charger) or radioactively labelled atoms
(epiphaniometer)

6. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Gas molecule-monomer interactions
Experimental observation
Figure: From A. Keller, M. Fierz, K. Siegmann, H.C. Siegmann, A.
Filippov, “Surface science with nanosized particles in a carrier gas”, J.
Vac. Sci. Technol. A 19(1), 1-8 (2001).

7. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Gas molecule-monomer interactions
Scaling law (1)
˜
Mass transfer coefficient Kk (∝ attachment probability)
times agglomerate mobility bk is independent of k for a
variety of aggregate sizes and shapes
˜
Kk
˜
Kk × bk = = constant
fk
Argument:
Attachment probability ∝ active surface, the surface area
accessible to diffusing molecules
Friction coefficient (inversely proportional to particle
mobility), ∝ active surface

8. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Gas molecule-monomer interactions
Scaling law (2)
Attachment probability is the gas-molecule monomer
collision probability (stricking coefficient of unity)
Molecular collision rate Kk with an aggregate consisting of
k monomers
Kk = ˆ
J · s dS
S
ˆ
J (steady-state) diffusive flux towards the aggregate, s unit
vector perpendicular to S
From the experimental scaling law
Kk fk βk
= = = ηk
kK1 kf1 β1
The calculation of the average monomer shielding factor
(and the ratios of the friction coefficients) reduces to
calculating relative molecular diffusive fluxes

9. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Gas molecule-monomer interactions
Diffusive flux
Molecular diffusive flux
J = −Dg ρ
Gas density from steady-state diffusion equation
(continuum regime)
2
Dg ρ(r) = 0
Boundary conditions
ρ → ρ∞ for |r| → ∞, and ρsur = 0 for r=S
Sticking probability unity, no multiple scattering events:
absorbing boundary conditions at the aggregate surface

10. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Linear chains: Effect of anisotropy
Linear chains: Numerical method (1)
Use the scaling law to determine the diffusion coefficient of
linear chains
The approach mimics closely the experimental procedure
Steady-state diffusion equation, with appropriate boundary
conditions, solved with the finite-element software Comsol
Multiphysics in cylindrical co-ordinates
Collision rate obtained by numerical integration of the
diffusive flux over the aggregate geometrical surface
Linear chains of up to k = 64

11. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Linear chains: Effect of anisotropy
Linear chains: Anisotropic friction coefficients
Linear chains are anisotropic
⊥
Anisotropic friction coefficients: βk , βk
Random orientations (Brownian motion)
⊥
3βk βk
βk =
⊥
βk + 2βk
Does the diffusive flux to a monomer have different
perpendicular and parallel components (anisotropic
fluxes)?

12. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Linear chains: Effect of anisotropy
Diffusive flux to a (spherical) monomer (3)
If the monomer is considered a rotation solid, the rotation
axis breaks rotational symmetry
Rotation (symmetry)
axis
(a) (b)
Rotation (symmetry)
axis

13. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Linear chains: Effect of anisotropy
Diffusive flux to a (spherical) monomer (2)
Perpendicular collision rate: diffusive flux perpendicular to
the rotation axis
⊥
K1 = ˆ
J · s⊥ dS = J⊥ dS = π 2 Dg R1 ρ∞
S S
Parallel collision rate: molecular flux parallel to the
symmetry axis
K1 = ˆ
J · s dS = J dS = 2πDg R1 ρ∞
S S
⊥
Explicit calculation confirms K1 = K1
Anisotropic shielding factors
⊥
βk K⊥ βk K
⊥
ηk = = k⊥ , ηk = = k
β1 kK1 β1 kK1

14. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Concentration field: dimer and 8-mer

15. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Parallel (axial) and perpendicular (radial) diffusive flux: dimer

16. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Parallel (axial) and perpendicular (radial) diffusive flux: 8-mer

17. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Monomer shielding factor in a linear chain (1)
Comparison with previous calculations (linear chains,
continuum regime)
Analytical solutions of the velocity field for steady-state
viscous flow (Stokes)
Happel and Brenner (1991): dimer
Filippov (2000): arbitrary aggregates of k spheres
Extrapolated experimental data: Dahneke (1982)
Creeping flow coupled to Darcy flow within the porous
aggregate
Vainshtein, Shapiro, and Gutfinger (2004)
Garcia-Ybarra, Castillo, and Rosner (2006)
and many others . . .

18. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Monomer shielding factor in a linear chain (2)
Filippov Happel Brenner Dahneke Collision Rate
β2 /β1 0.692 0.694
β3 /β1 0.569 0.574
β4 /β1 0.507 0.507
β5 /β1 0.461 0.463
β8 /β1 0.390 0.389
β2 /β1 0.645 0.639 0.633
β8 /β1 0.324 0.313
⊥
β2 /β1 0.716 0.719 0.725
⊥
β8 /β1 0.435 0.434 0.428

19. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Anisotropic friction coefficient
Diffusion simulations Diffusion simulations
0.7
Fit Fit
0.6
Vainshtein et al. Vainshtein et al.
0.6
0.5
β⊥ β1
β|| β1
0.5
0.4
n
n
0.4
0.3
0.3
0.2
0 10 20 30 40 50 60 0 10 20 30 40 50 60
n n

20. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Numerical results
Isotropic friction coefficient, Mobility radius
0.7
14
Diffusion simulations
βn from βn and β⊥
||
n
12
0.6
10
0.5
βn β1
rn r1
8
0.4
6
4
0.3
2
0 10 20 30 40 50 60 0 10 20 30 40 50 60
n n
⊥
βk obtained from βk and βk for random aggregate
orientations
Ideal clusters: mobility radius Rk /R1 = k

21. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Shielded Langevin equations
Monomer Langevin equations of motion (1)
3d equations of motion for the i-th monomer in a
k -monomer linear chain
m1¨i = Fi − β1i m1 ri + Wi (t)
r ˙
Intra-chain isotropic friction coefficient β1i
β1i K1i 1
= ≡ η1i ; ηk = η1i
β1 K1 k
i=1,k
Steady-state collision rate K1i on the i-monomer
Fluctuation Dissipation Theorem
Wij (t)Wij (t ) = Γi δii δjj δ(t − t )
Γi = 2β1i m1 kB T = 2η1i β1 m1 kB T

22. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Shielded Langevin equations
Langevin Dynamics: Diffusion coefficient of a linear chain (1)
Mean-square displacement of chains: k = 5, 8 monomers
2
lim δRCM (t) = 6Dk t
t→∞
125
n=8
n=5
Linear fit for n=8
Linear fit for n=5
100
75
〈δr2 〉 d2
CM 1
50
25
0
0 20 40 60 80 100
β1t

23. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Shielded Langevin equations
Langevin simulations: Diffusion coefficient of a linear chain (2)
Ratios of diffusion coefficients
Collision Rate Langevin simulations
D5 /D1 0.432 0.428
D8 /D1 0.321 0.319
Equivalent descriptions
Aggregate diffusion in terms of an average monomer
shielding factor, Fluctuation Dissipation Theorem applies to
the whole aggregate
Individual monomer shielding factor, Fluctuation Dissipation
Theorem applies to each monomer in the aggregate

24. Motivation Dynamics of linear chains Langevin simulations Revisited Conclusions
Conclusions
Importance of the shielding factor of a monomer in an
aggregate
Active surface may be a useful concept
Diffusion and friction coefficients may be obtained from the
calculation of the molecular collision rate to an aggregate
Calculated coefficients in reasonable agreement with
previous theoretical calculations
Approach is based on mass transfer only, momentum
transfer is treated approximately
Not clear whether this approach may be coupled to
simulations of aggregate formation by Langevin dynamics