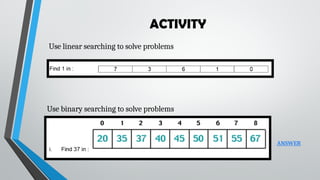
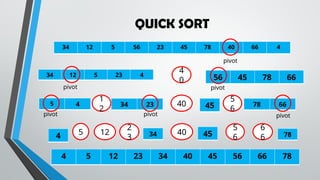
The document explains sorting and searching algorithms, detailing various sorting methods such as selection sort, merge sort, bubble sort, quick sort, and insertion sort, along with their advantages and disadvantages. Additionally, it covers searching techniques including linear search and binary search, highlighting their applicability based on data organization. Students are encouraged to learn these algorithms and apply them through various activities.

1. DFC30233
DATA STRUCTURES
CHAPTER 6
SORTING & SEARCHING
Prepared by: Ts. Maznah
Ahmad

2. LEARNING OUTCOME
Student should able to:
Define sorting
Explain various method of sorting
Selection sort
Merge Sort
Bubble Sort
Quick Sort
Insertion Sort
Define Searching
Explain types of searching:
Linear
Binary

3. PART 1 - SORTING

4. What can you conclude from the image?

5. Why we need to sort data?
• Sorting a large number of items can take a substantial
amount of computing resources.
• For small collections, a complex sorting method may be
more trouble than it is worth.

6. DEFINITION
• Sorting is the process of arranging a list of elements in a
particular order (Ascending or Descending).

7. VARIOUS TYPE OF SORTING
• Selection Sort
• Merge Sort
• Bubble Sort
• Quick Sort
• Insertion Sort

8. SELECTION SORT
•Selection sort is a sorting algorithm, specifically an in-
place comparison sort.
•Selection sort is noted for its simplicity, and also has
performance advantages over more complicated
algorithms in certain situations.
•Step: 1. Find the smallest element, and put it to
the first position.
•2. Find the next smallest element, and put it to
the second position.
•3. Repeat until all elements are in the right
positions.

9. SELECTION SORT

10. INSERTION SORT
• Insertion sort is a comparison sort in which the sorted array (or list)
is built one entry at a time.
• It is much less efficient on large lists than more advanced algorithms.
• Step:
1.Take the first element as a sorted sub-array.
2. Insert the second element into the sorted sub-array (shift
elements
if needed).
3. Insert the third element into the sorted sub-array.
4. Repeat until all elements are inserted.

11. INSERTION SORT
34 12 5 56 23 45
34 12 5 56 23 45
12 34 5 56 23 45
5 12 34 56 23 45
5 12 34 56 23 45
5 12 23 34 56 45
5 12 23 34 45 56

12. MERGE SORT
•Merge sort is a comparison-based sorting algorithm.
•Merge sort is a divide and conquer algorithm. The
divide-and-conquer paradigm involves:
• Conceptually, a merge sort works as follows:
1. Divide the n-element sequence to be sorted into
two subsequences of n/2 elements each.
2. Sort the two subsequences recursively by re-applying
merge sort.
3. Merge the two sorted subsequences to produce the
sorted answer.

13. MERGE SORT
45 21 5 17 84 56 14
45 21 5 17 84 56 14
45 21 5 56 14
17 84
5 14
56
84
17
21
45
21 45 5 17 84 14 56
5 21 45 14 17 56 84
5 14 17 21 45 56 84

14. BUBBLE SORT
• The bubble sort works by repeatedly swapping adjacent elements
that are not in order until the whole list of items is in sequence.
• Step:
1. Scan the array, swapping adjacent pair of elements if
they are not in relative order. This bubbles up the largest
element to the end.
2. Scan the array again, bubbling up the second largest
element.
3. Repeat until all elements are in order.

15. ADVANTAGES & DISADVANTAGES
ADVANTAGES DISADVANTAGES
The primary advantage of the
bubble sort is that it is popular
and easy to implement.
the fact that it does not deal well with a list
containing a huge number of items. This
is because the bubble sort requires n-
squared processing steps for every n
number of elements to be sorted
Furthermore, in the bubble sort,
elements are swapped in place
without using additional
temporary storage, so the space
requirement is at a minimum.
As such, the bubble sort is mostly suitable
for academic teaching but not for real-life
applications.

16. BUBBLE SORT

17. BUBBLE SORT

18. BUBBLE SORT

19. QUICK SORT
• The basic concept is to pick one of the elements in the array as a
pivot value around which the other elements will be rearranged.
• Everything less than the pivot is moved left of the pivot (into the
left partition).
• Similarly, everything greater than the pivot goes into the right
partition. At this point each partition is recursively quick sorted.

20. ADVANTAGES & DISADVANTAGES
ADVANTAGES DISADVANTAGES
This is faster sorting
method among all.
It is complex method of
sorting so, it is little hard to
implement than other
sorting methods.
Its efficiency is also
relatively good.
It requires relatively
small amount of
memory.

21. QUICK SORT
34 12 5 56 23 45 78 40 66 4
4
0
34 12 5 23 4
56 45 78 66
40
5
6
1
2
5 4 34 23 78 66
45
40
5
6
12
5
2
3
6
6
4 34 45 78
4 5 12 23 34 40 45 56 66 78
pivot
pivot
pivot
pivot pivot
pivot

22. ACTIVITY
1. Show the procedure to sort the items below using selection sort.
2. Show the procedure to sort the items below using merge sort.
3. Show the procedure to sort the items below using bubble sort.
4. Show the procedure to sort the items below using quick sort.
13 6 21 18 9 4 8 20
6 1 2 3 4 5
5 8 1 3 7 10 2
42 16 84 12 77 26 53

23. PART 2 - SEARCHING

24. DEFINITION
•Process of finding an element within the list of elements
in order or randomly.
•Retrieval: Successful Search
•A table of records in which a key is used for retrieval is
often called a SEARCH TABLE or DICTIONARY.
•Internal Searching – Whole data in main memory
•External Searching – Most data is kept in auxiliary
memory

25. SEARCHING METHODS
•Sequential or Linear Searching
•Binary Search
•Hashing

26. LINEAR SEARCH
• The linear Search is can be used whenever the list is in order or
not ordered.
• It is simple and good for small lists.
• Mostly used when data is not sorted.
• Less efficient if list is large.
• In linear search, we start searching for the target at the beginning
of the list and continue until we find the target or we are sure
that it is not in the list.

27. LINEAR SEARCH
ADVANTAGES DISADVANTAGES
It is simple and conventional
method of searching data.
The linear or sequential name
implies that the items are
stored in a systematic manner.
This method is insufficient when
large number of elements is
present in list.
The elements in the list can be
in any order. i.e. The linear
search can be applied on
sorted or unsorted linear data
structure.
It consumes more time and
reduces the retrieval rate of the
system.

28. LINEAR SEARCH

29. LINEAR SEARCH

30. LINEAR SEARCH

31. LINEAR SEARCH

32. Linear Search

33. BINARY SEARCH
• This technique works on sorted lists and can be applied only on
sorted list.
• Not applied on Linked Lists.
• Requires less number of comparisons than linear search.
• The binary search starts by testing the data in the element at the
middle of the array to determine if the target is in the first or
second half of the list.
• If it is in the first half, we do not need to check the second half.
• If it is in the second half, we do not need to test the first half. In
other words, we eliminate half the list from further consideration

34. BINARY SEARCH
Let say, we want to search whether 21 is in the list
4 7 8 10 14 21 22 36 62 77
First determine the middle(pivot) of the list using this formula:
middle = (lowest index) + ( highest index) /2
In this example it will be :
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
4 7 8 10 14 21 22 36 62 77
(0 + 9)/ 2 = 4.5
M= 4

35. BINARY SEARCH
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
4 7 8 10 14 21 22 36 62 77
F M L
Key = 21
M = 14
21 != 14
21>14
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
4 7 8 10 14 21 22 36 62 77

36. BINARY SEARCH
[5] [6] [7] [8] [9]
21 22 36 62 77
(5 + 9)/ 2 = 7
M= 7
Key = 21
M = 36
21 != 36
21<36
[5] [6] [7] [8] [9]
21 22 36 62 77
F M L

37. BINARY SEARCH
[5] [6]
21 22
(5 + 6)/ 2 = 5.5
M= 5
Key = 21
M = 21
21 = 21
Searching stop and successful
F M L

38. ACTIVITY
Use linear searching to solve problems
ANSWER
Use binary searching to solve problems

39. ACTIVITY
Determine whether 75 is in the list or not.

40. • http://interactivepython.org/courselib/static/pythonds/
SortSearch/Hashing.html