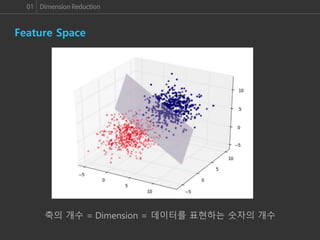
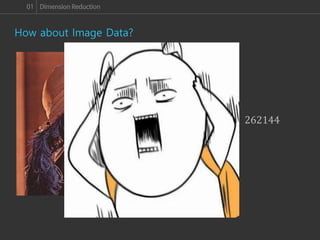
패턴을 인식하는 데 있어서 가장 기본적으로 알아야 하는 개념은 바로 Feature 공간입니다. 이미지 패턴 인식을 할 때에도 각 이미지를 Feature 공간 안에 배치한 후에 패턴을 인식하게 되는데, 불행히도 이미지는 고차원의 정보이기 때문에 우리가 실제로 느낄 수 있는 차원을 훨씬 뛰어넘는 공간에 배치 되어, 직관적인 패턴 분석이 많이 어렵습니다.
그렇기 때문에 PCA처럼 고차원 데이터를 저차원의 공간으로 Projection 하여 Visualization 하기 위한 수많은 연구들이 진행되어 왔고, 실제로 논문에서 실험 결과를 Visualization 하여 이해를 돕거나, 패턴을 분석하기 전에 데이터들이 어떠한 모양으로 분포하고 있는지에 대한 정보를 얻어 분석 방향을 결정하기도 하였습니다.
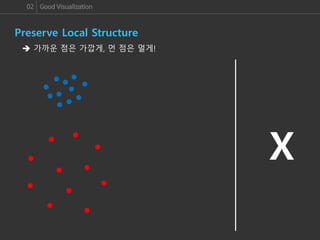
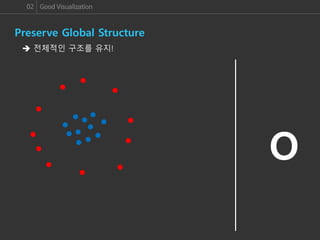
이번 세미나에서는 여러 Dimension Reduction 알고리즘들을 알아보고, 그 중에서도 좋은 성능을 자랑하는 알고리즘 중의 하나인 Nonlinear & Non-parametric Visualization 알고리즘인 t-SNE 알고리즘에 대해 살펴보겠습니다. 그리고 이러한 알고리즘들이 Dimension Reduction의 중요한 Point인 Global & Local 관계의 유지와 Manifold data의 Visualization을 얼마나 잘 수행하는지 알아보도록 하겠습니다.