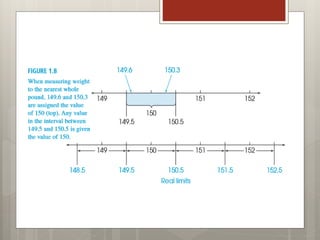
The document defines key concepts in data classification including scores, data sets, variables, and levels of measurement. It explains that a score is a measurement of an individual, the data set is the complete set of scores, and a variable is a characteristic that can differ between individuals. Variables can be qualitative or quantitative, discrete or continuous. The levels of measurement are nominal, ordinal, interval, and ratio. The document also introduces common statistical notations used to represent variables, sample sizes, and sums.