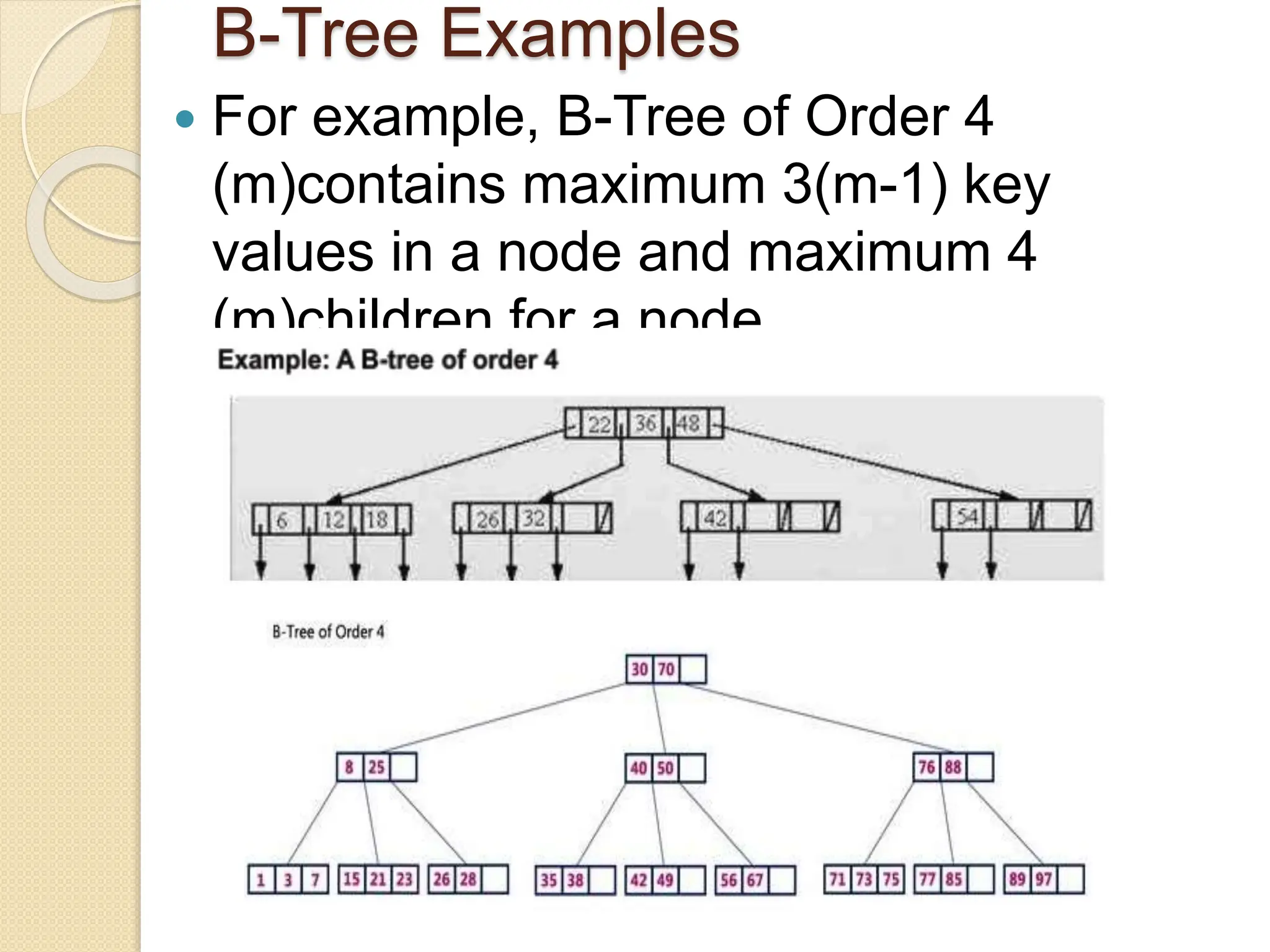
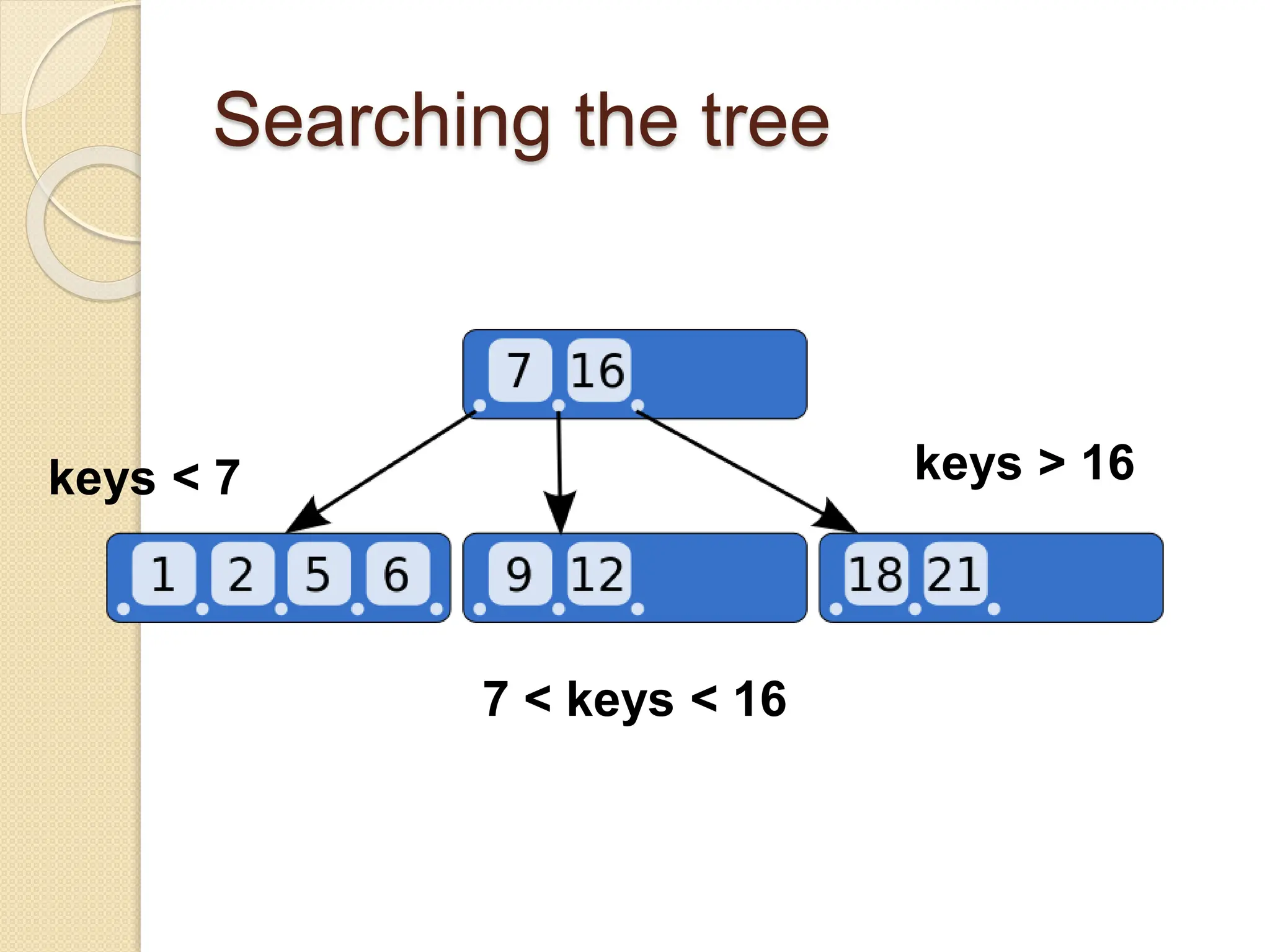
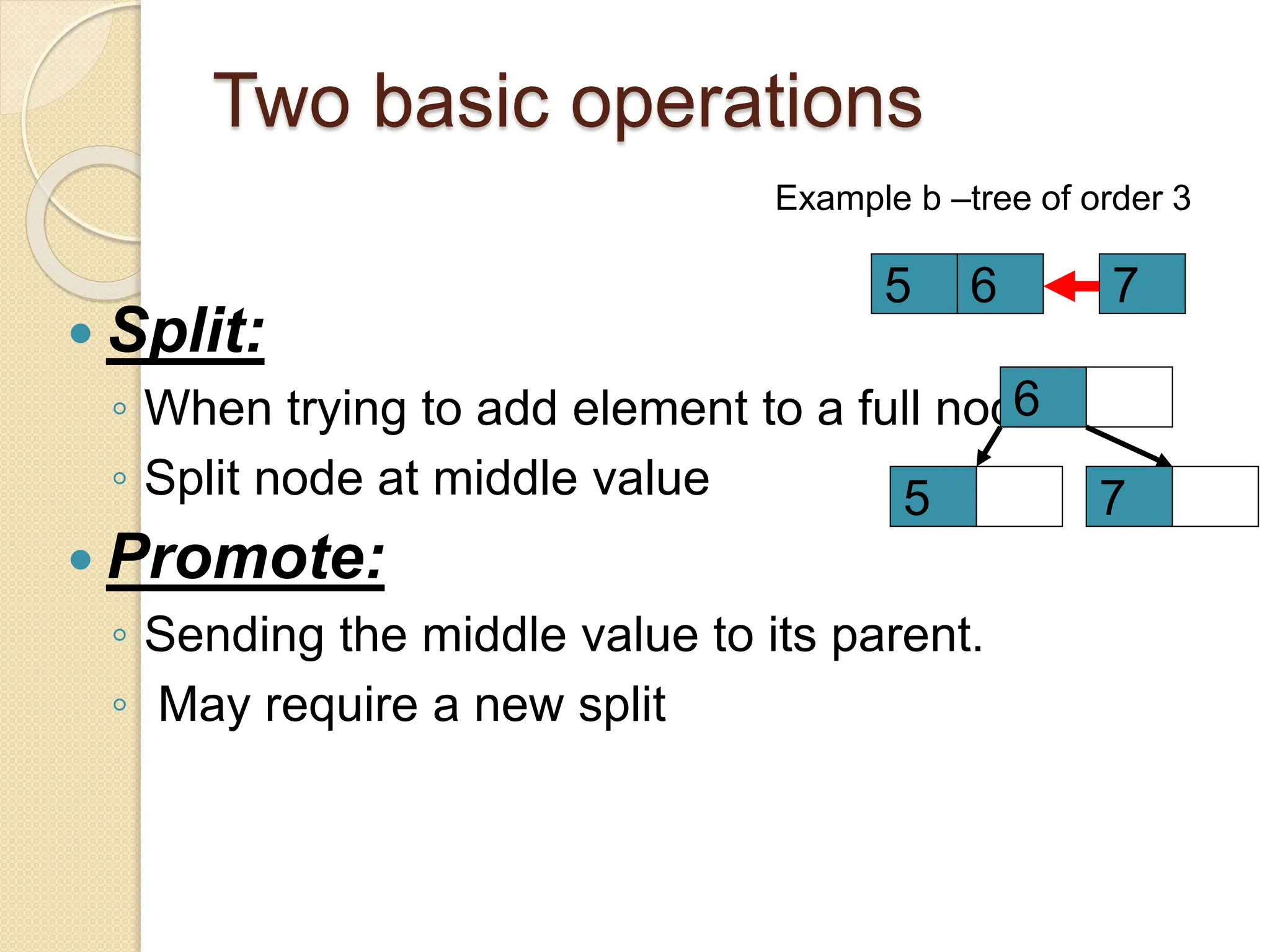
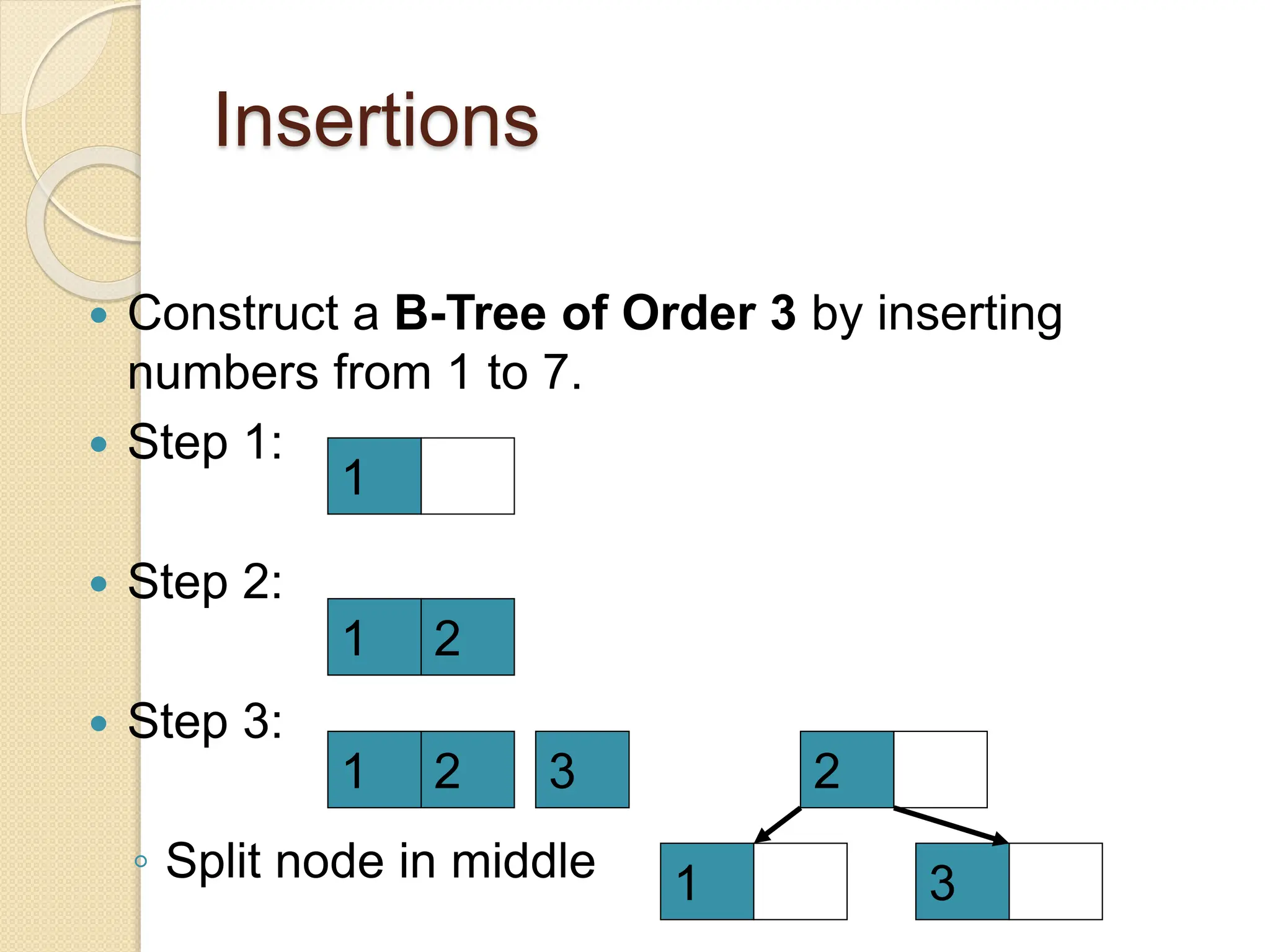
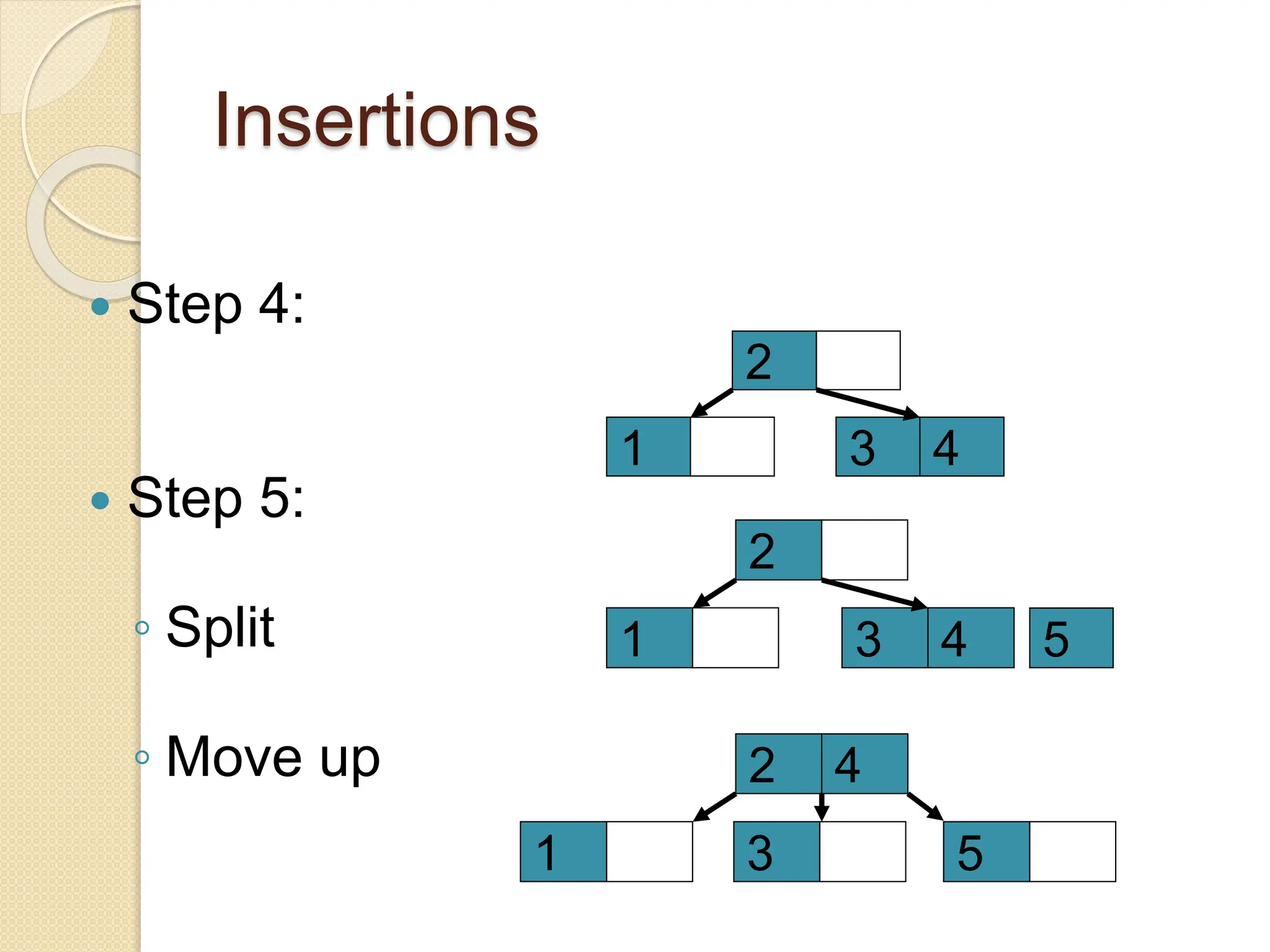
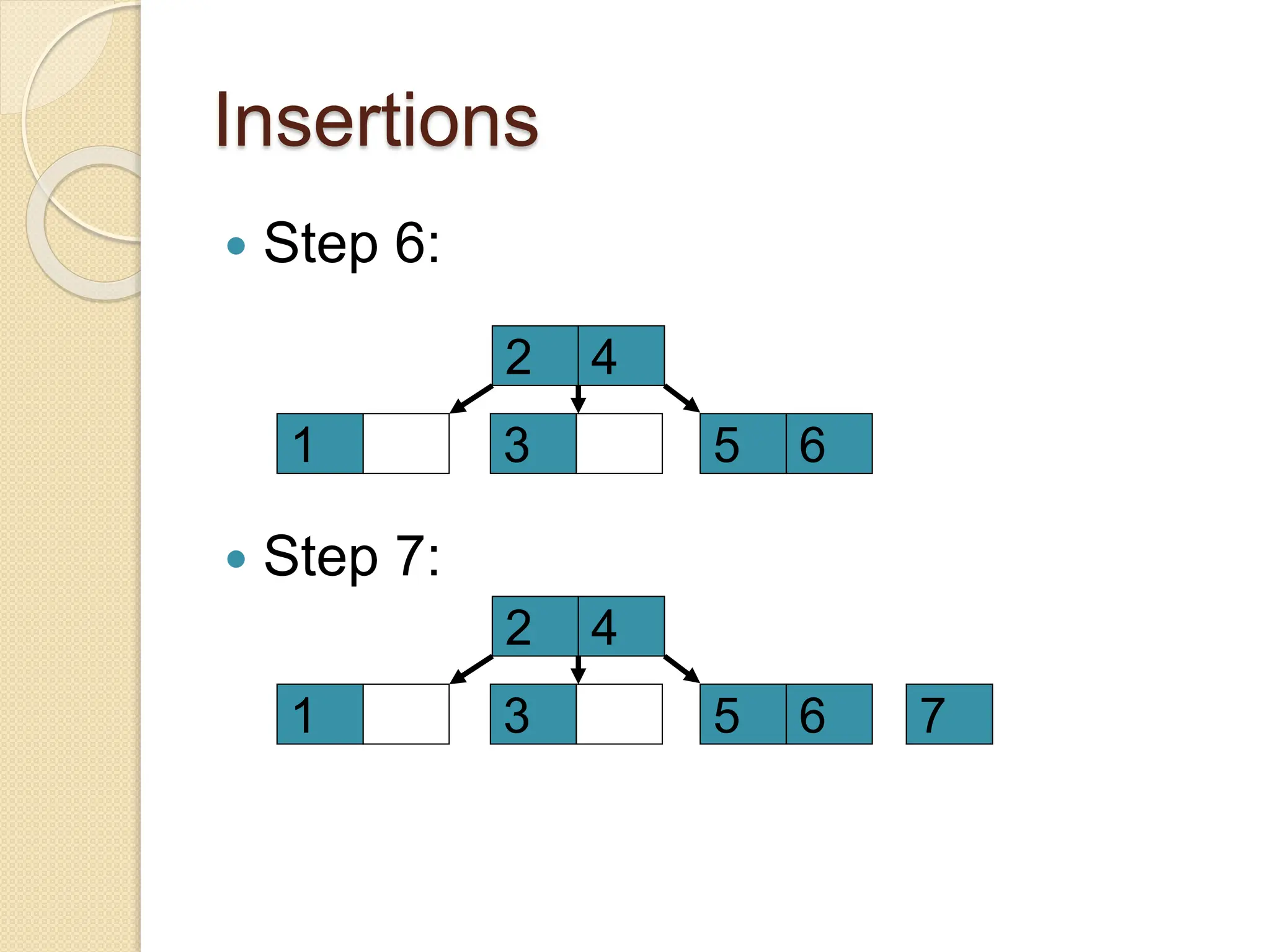
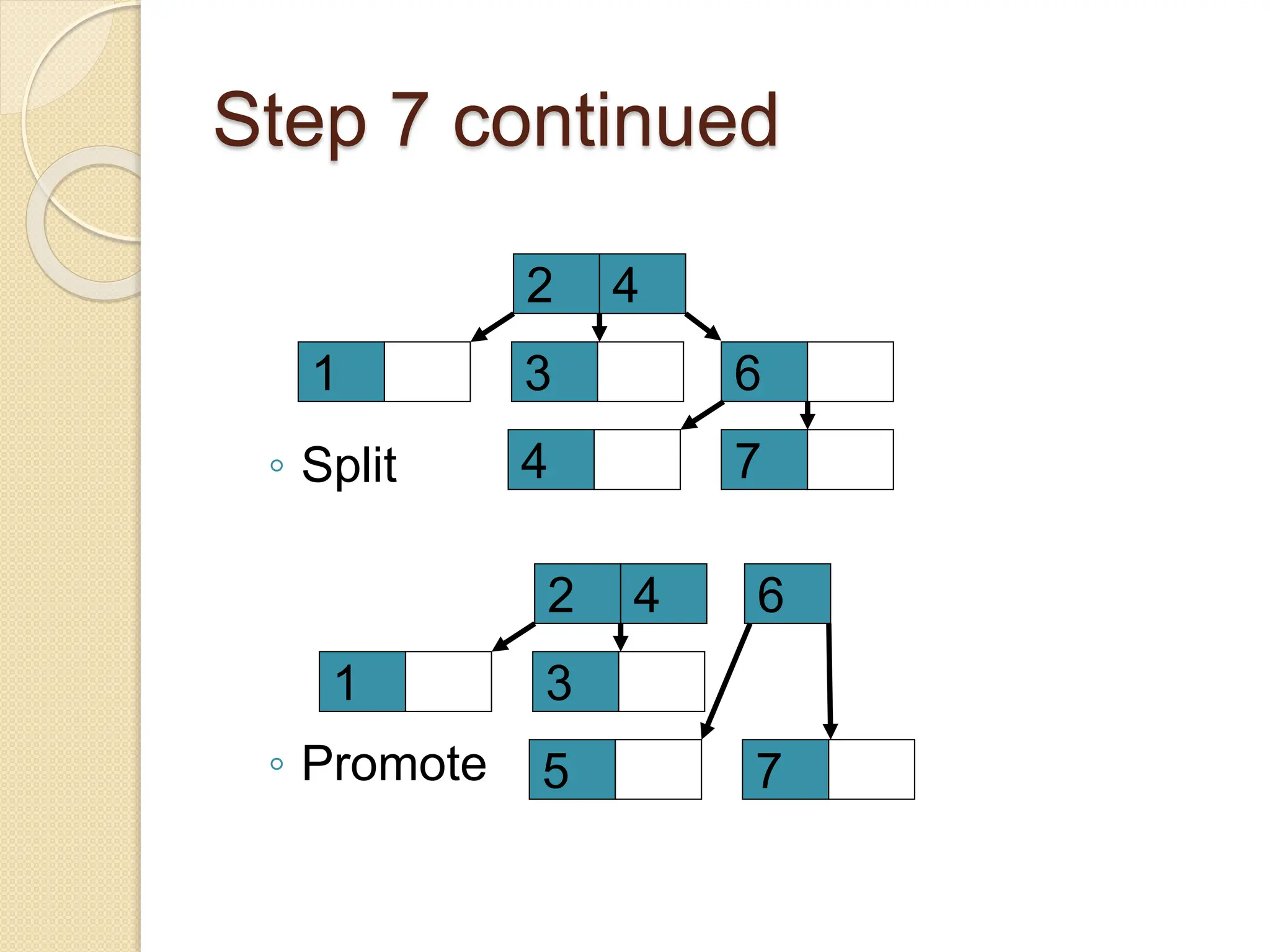
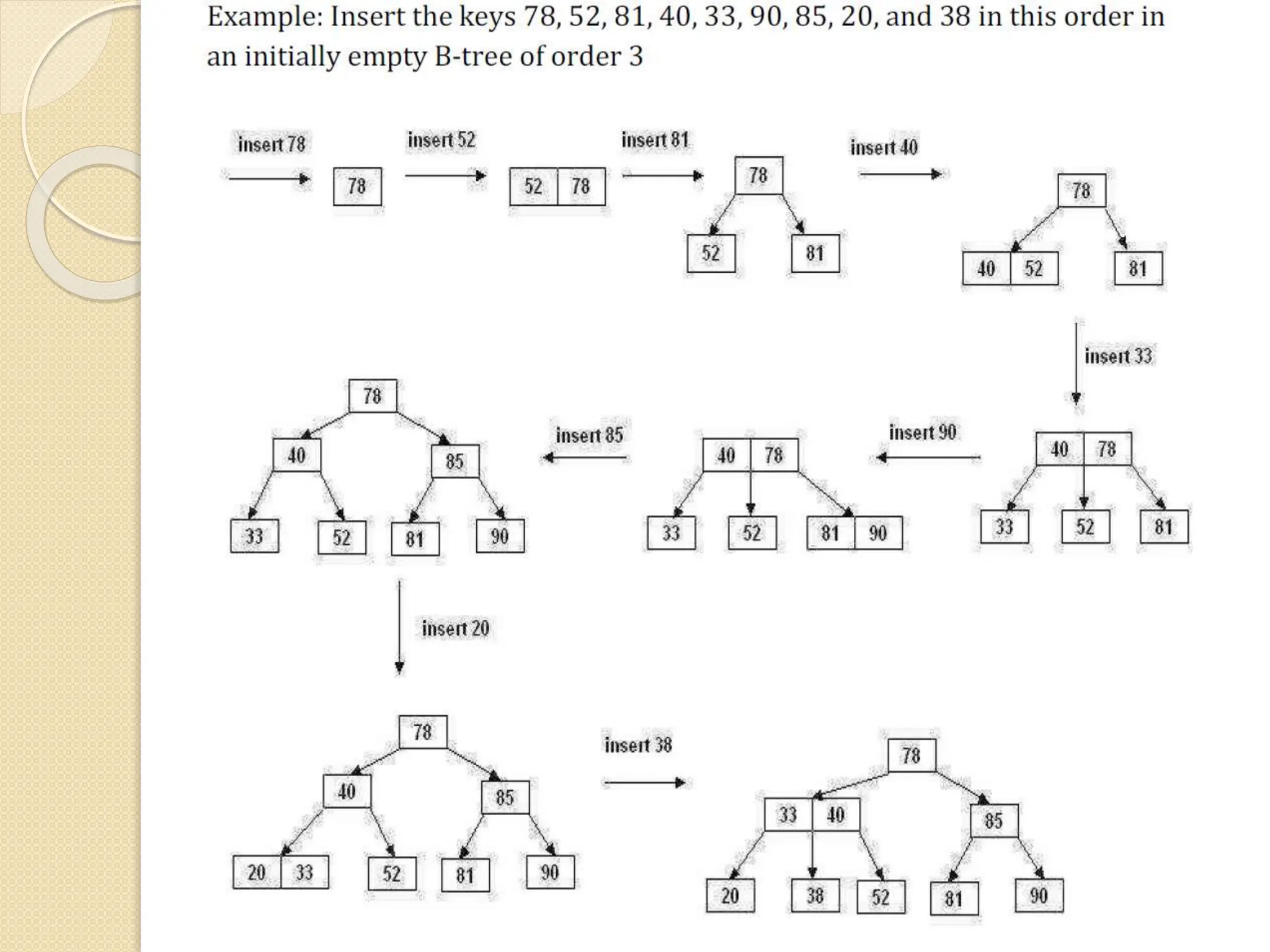
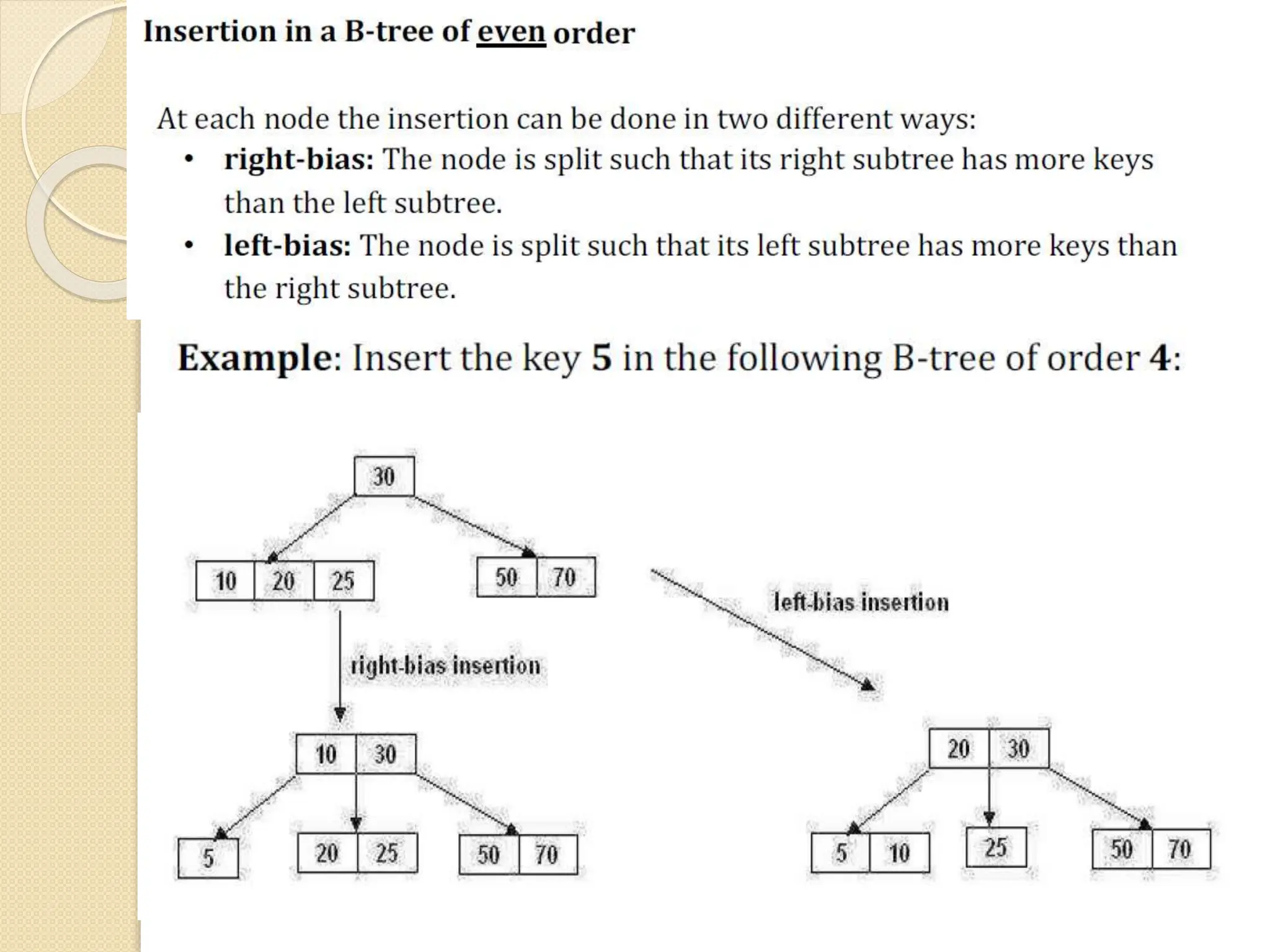
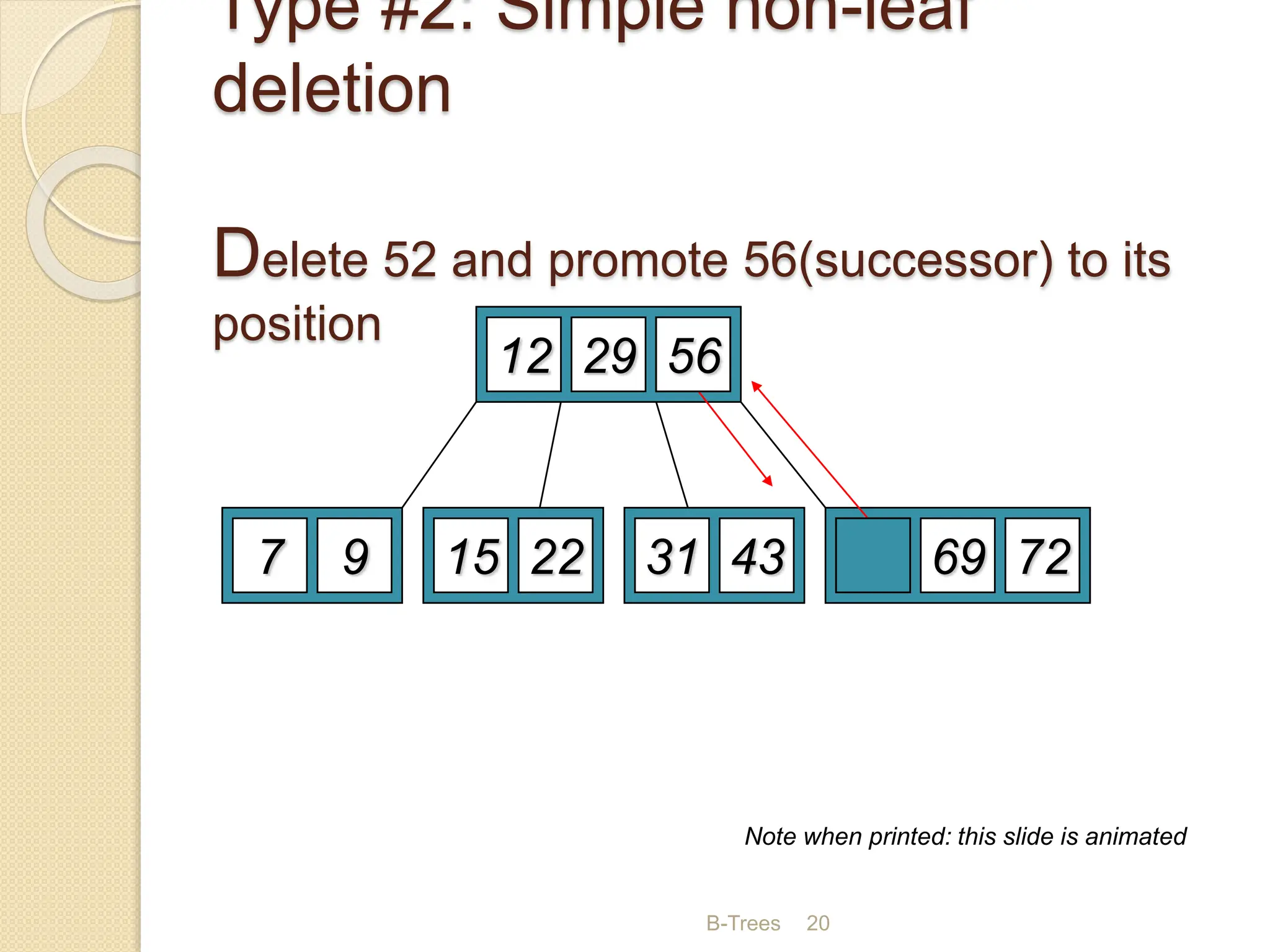
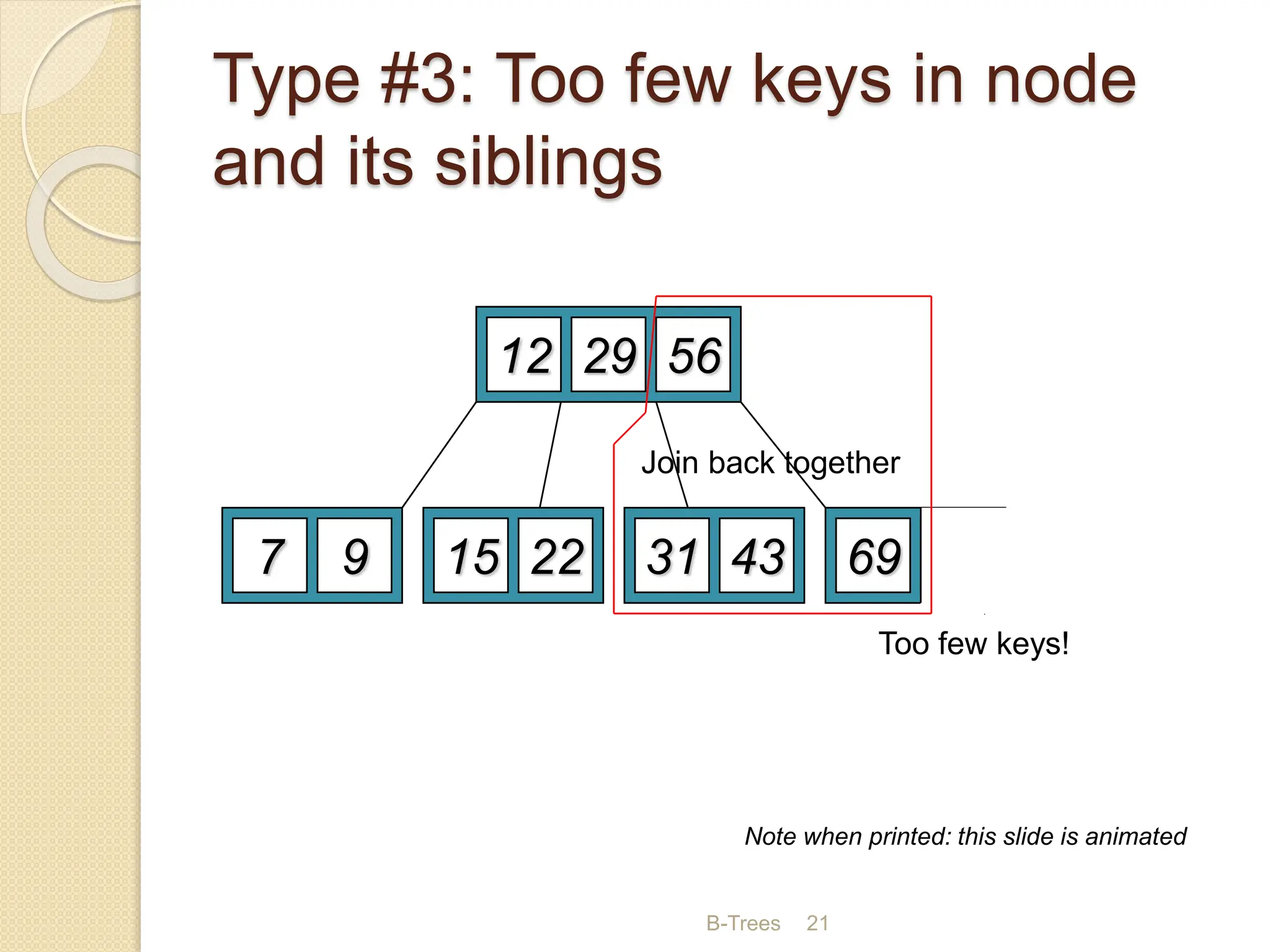
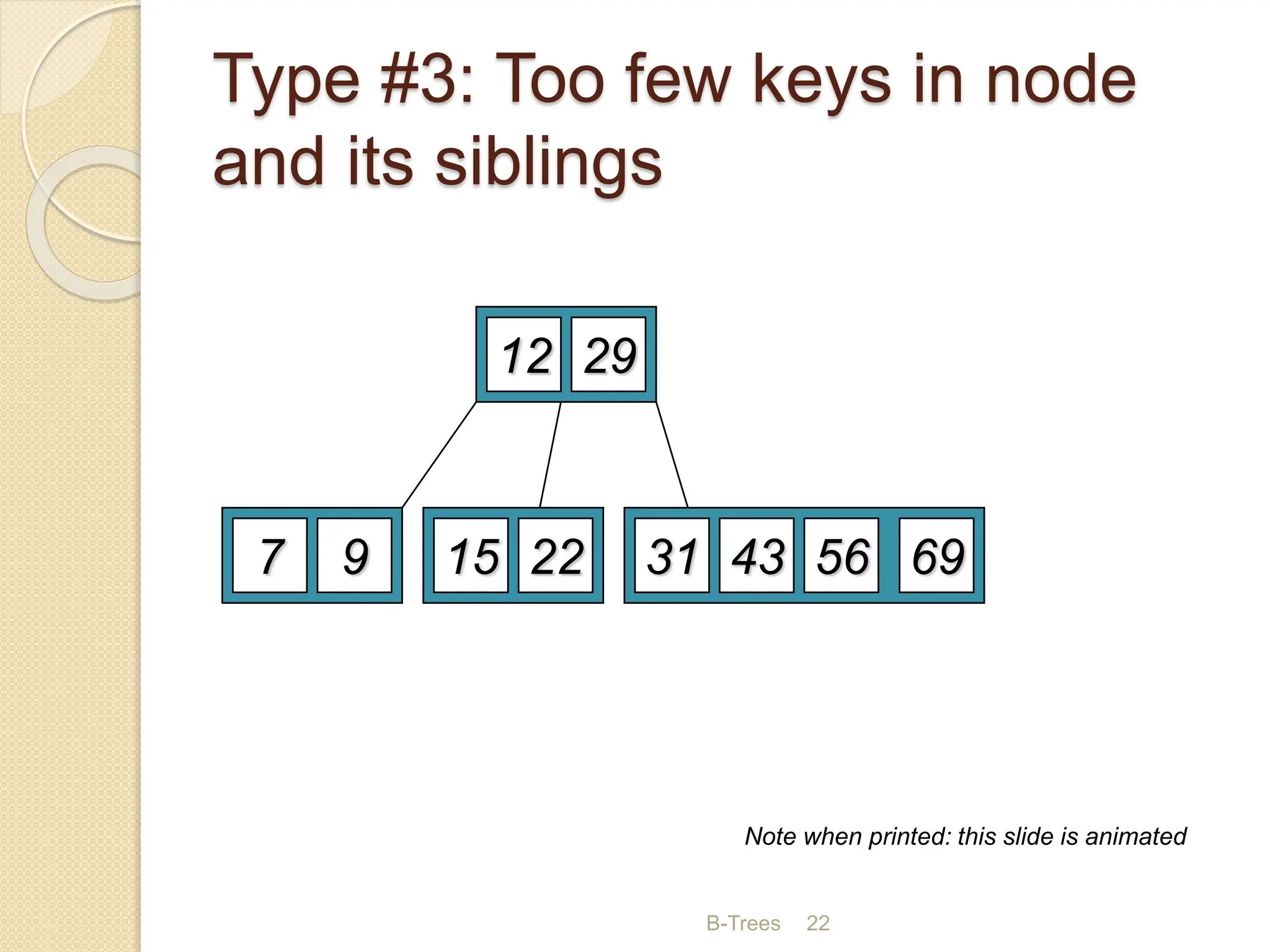
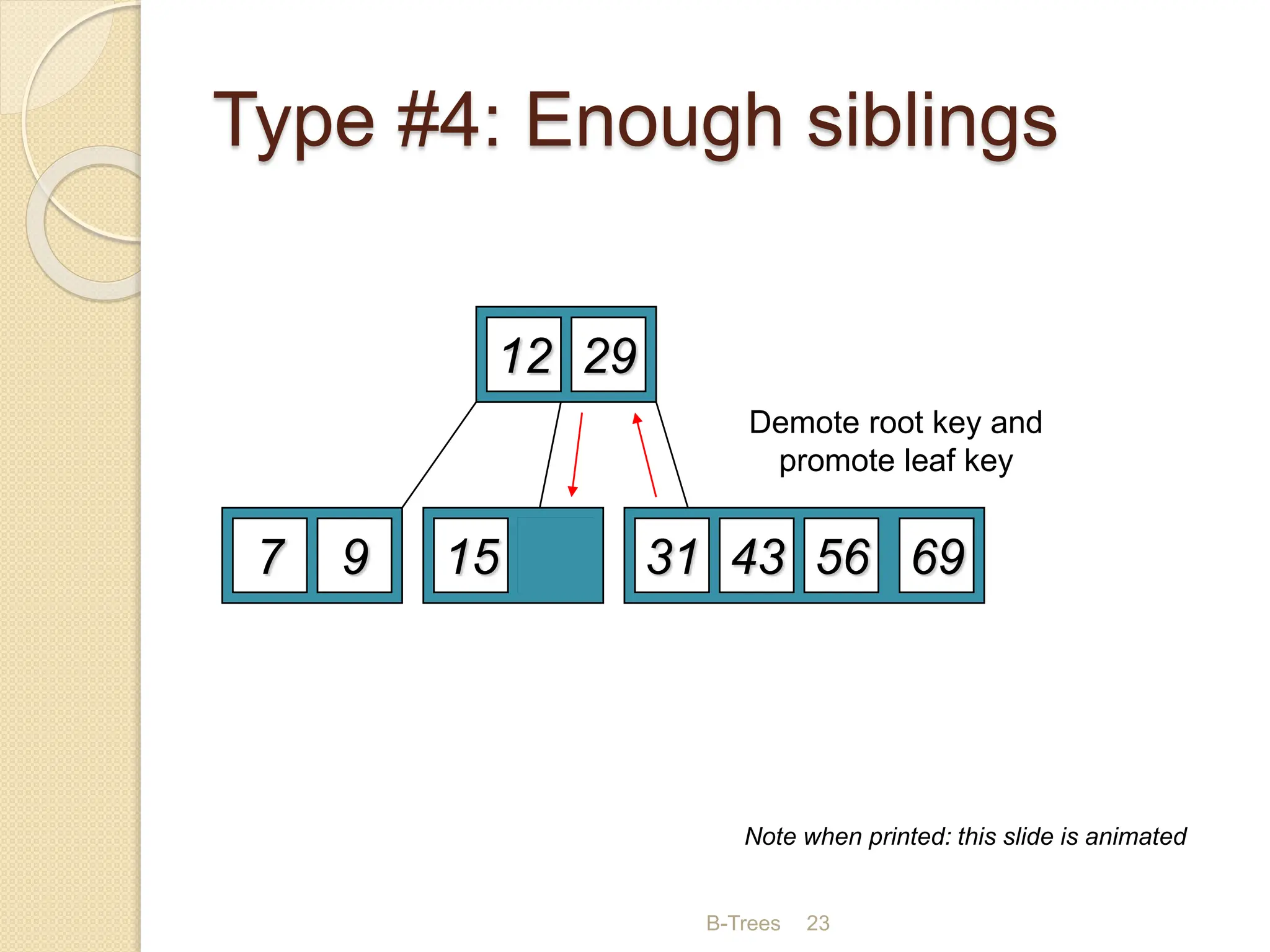
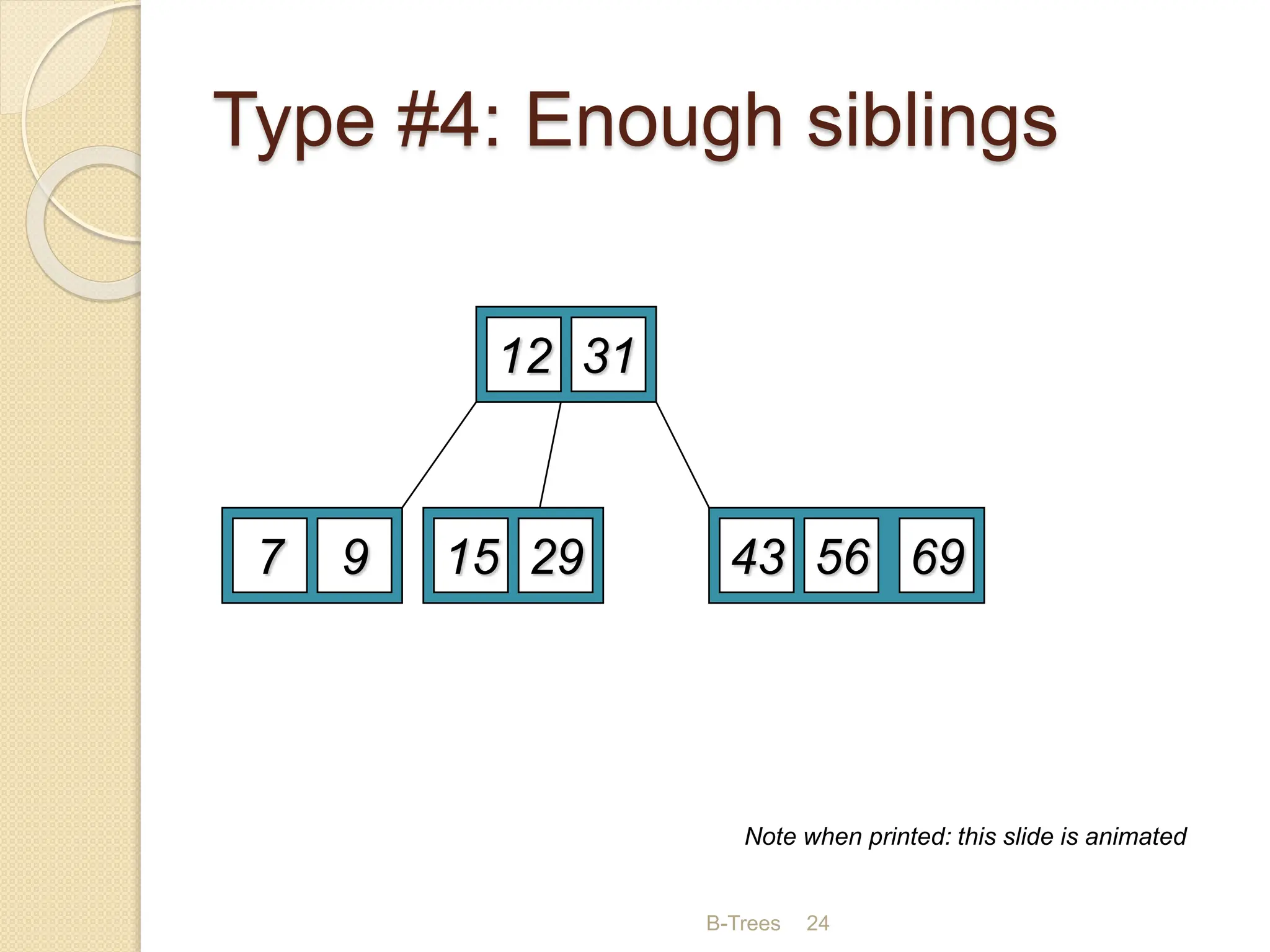
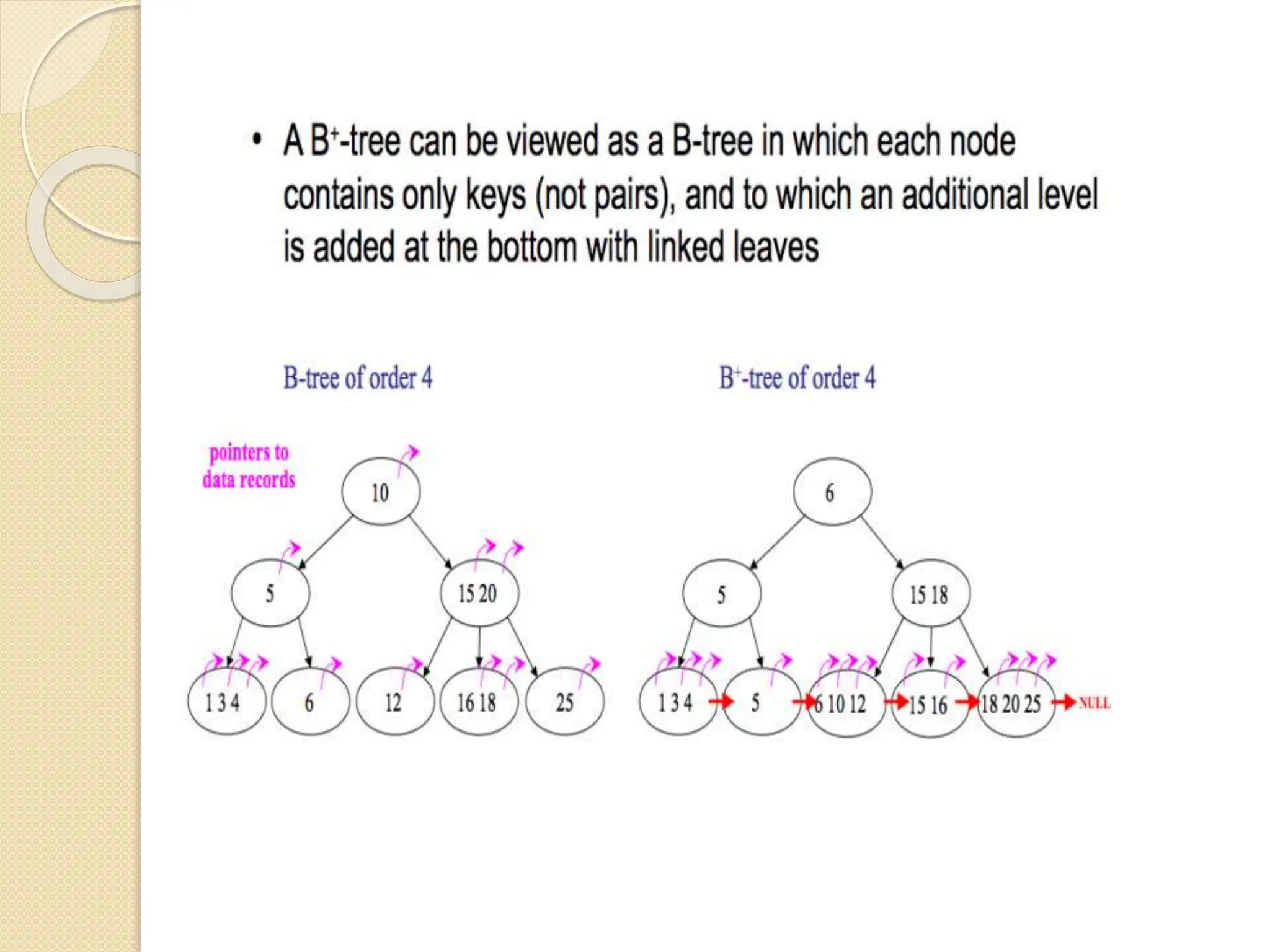
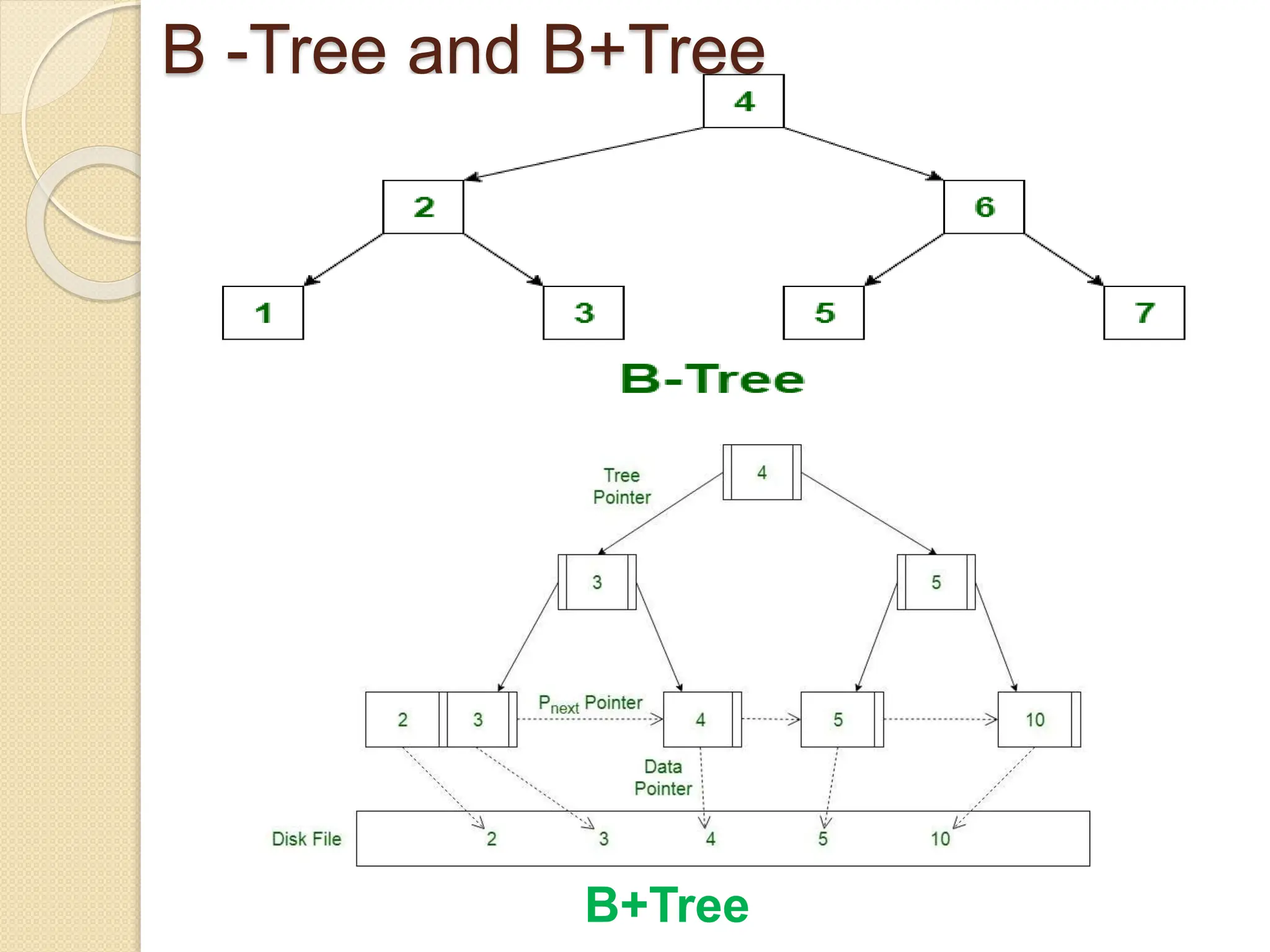
B-Trees and B+ Trees are data structures used to store large amounts of data on disks when it cannot all fit in main memory. They allow for efficient multilevel indexing and reduce disk access times compared to other balanced trees like AVL trees by keeping the tree height low. B-Trees have multiple keys in each node and store data pointers in internal and leaf nodes, while B+ Trees only store data pointers in leaf nodes. B+ Trees provide faster searches and easier insertion/deletion compared to B-Trees. Both are commonly used in database systems and file systems to efficiently organize and retrieve large blocks of indexed data from secondary storage.

1. Data Structures
(B-Tree and B+ Tree )
Dr.N.S.Nithya
ASP/CSE

2. B-Tree
 B Tree & B+ Tree Data Structures are used to
Store Data in Disks When the Entire Data Cannot
be Stored in the Main Memory. Both are used for
multilevel indexing
Two main reason for implementing B-Tree
1. When the amount of data to be stored is very high,
we cannot store the entire data in the main memory.
Hence we store data in the disk. Data access from
the disk takes more time when compared to the
main memory access.
2.When the number of keys of the data stored in disks is
very high, the data is usually accessed in the form of
blocks. The time to access these blocks is directly
proportional to the height of the tree.
In AVL and Splay Tree has a binary structure of storing
only two values . B-trees are used to store more than

3. B-Tree
 B-Tree can be defined as a self-balanced
search tree with multiple keys in every node
and more than two children for every node.
 Here, number of keys in a node and number
of children for a node is depend on the
order of the B-Tree. Every B-Tree has order.
 AS more number of keys are placed in each
node of the B-Tree, the height of the B tree
is kept to a minimum.
 The main idea of using B-Trees is to reduce
the number of disk accesses.
 By keeping the height of the B-tree to the
minimum, the access is faster when
compared to other balanced trees like AVL
trees.

4. Representation of B-Tree
Ki are the search-key values (More than
one key value)
Pi are pointers to children (for non-leaf
nodes) or pointers to records (for leaf
nodes).
The search-keys in a node are ordered
(Ascending order)
K1 < K2 < K3 < . . . < Kn–1

5. Properties of the B-Tree
 All the leaf nodes must be at same level.
 All nodes except root must have at least
[m/2]-1 keys and maximum of m-1 keys.
 All non leaf nodes except root (i.e. all
internal nodes) must have at least m/2
children.
 The root node must have at least 2
children.
 A non leaf node with n-1 keys must have
n number of children.
 All the key values within a node must be
in Ascending Order.

6. B-Tree Examples
 For example, B-Tree of Order 4
(m)contains maximum 3(m-1) key
values in a node and maximum 4
(m)children for a node.

7. Basic Operations Of B-
Tree
Searching
Insertion (check
overflow)
Deletion (check
underflow)

8. Searching
 Searching in B tree is similar to that in
BST.
 In a Binary search tree, the search
process starts from the root node and
we make a 2-way decision every time
(we go to either left subtree or right
subtree).
 In B-Tree also search process starts
from the root node but here we make an
n-way decision every time. Where 'n' is
the total number of children the node

9. Searching the tree
keys < 7 keys > 16
7 < keys < 16

10. Insertion
 In a B-Tree, a new element must be added
only at the leaf node .
 When you are inserting a element in to a
leaf node ,check the node is full or not
 if number of keys=m-1 (m is order of tree)
,the node is full.
If the node is full then the following
operations are to be performed until the b-
tree property satisfies in all the level.
 Split
 Promote

11. Two basic operations
Example b –tree of order 3
 Split:
◦ When trying to add element to a full node
◦ Split node at middle value
 Promote:
◦ Sending the middle value to its parent.
◦ May require a new split
7
5
6
6
5 7

12. Insertions
 Construct a B-Tree of Order 3 by inserting
numbers from 1 to 7.
 Step 1:
 Step 2:
 Step 3:
◦ Split node in middle
1
1 2
1 2 3 2
1 3

13. Insertions
 Step 4:
 Step 5:
◦ Split
◦ Move up
5
3
2
1 4
3
2
1 4
4
2
1 3 5

14. Insertions
 Step 6:
 Step 7:
4
2
1 3 5 6
4
2
1 3 5 6 7

15. Step 7 continued
4
2
1 3 6
4 7
4
2
1 3
6
5 7
◦ Split
◦ Promote

18. Deletion
 For deletion we have to check underflow
Number of keys < m-1/2
 Case1: Leaf node with no underflow –
Delete the key
 Case2: Non-leaf node with underflow -
Delete the key and promote the
predecessor or successor key to the non-
leaf deleted key’s position.
 Case3:leaf node with few key sibling –
merge with the sibling
 Case4:leaf node with enough sibling-
Demote root key and promote leaf key

19. B-Trees 19
Type #1: Simple leaf deletion
12 29 52
2 7 9 15 22 56 69 72
31 43
Delete 2: Since there are enough
keys in the node, just delete it
Assuming a 4-way
B-Tree, as before...
Note when printed: this slide is animated

20. B-Trees 20
Type #2: Simple non-leaf
deletion
Delete 52 and promote 56(successor) to its
position
12 29 52
7 9 15 22 56 69 72
31 43
Delete 52
Borrow the predecessor
or (in this case) successor
56
Note when printed: this slide is animated

21. B-Trees 21
Type #3: Too few keys in node
and its siblings
12 29 56
7 9 15 22 69 72
31 43
Delete 72
Too few keys!
Join back together
Note when printed: this slide is animated

22. B-Trees 22
Type #3: Too few keys in node
and its siblings
12 29
7 9 15 22 69
56
31 43
Note when printed: this slide is animated

23. B-Trees 23
Type #4: Enough siblings
12 29
7 9 15 22 69
56
31 43
Delete 22
Demote root key and
promote leaf key
Note when printed: this slide is animated

24. B-Trees 24
Type #4: Enough siblings
12
29
7 9 15
31
69
56
43
Note when printed: this slide is animated

25. B+Tree
To implement dynamic multilevel indexing,
B-Tree and B+ tree are generally employed.
Drawback of B-tree
It stores the data pointer in each node at all
level. This will increase the number of level in
the tree thereby increase the searching time of
record.
B+ tree eliminates the above drawback by
storing data pointers only at the leaf nodes
of the tree.
The leaf nodes, therefore form the first
level of index, with the internal nodes

27. B -Tree and B+Tree
B+Tree

28. Difference between B-Tree and B+Tree
S.No B TREE B+ TREE
1.
All internal and leaf nodes have data
pointers
Only leaf nodes have data
pointers
2.
Since all keys are not available at leaf,
search often takes more time.
All keys are at leaf nodes, hence
search is faster and accurate..
3.
No duplicate of keys is maintained in the
tree.
Duplicate of keys are maintained
and all nodes are present at leaf.
4.
Insertion takes more time and it is not
predictable sometimes.
Insertion is easier and the results
are always the same.
5.
Deletion of internal node is very complex
and tree has to undergo lot of
transformations.
Deletion of any node is easy
because all node are found at leaf.
6.
Leaf nodes are not stored as structural
linked list.
Leaf nodes are stored as structural
linked list.
7. No redundant search keys are present..
Redundant search keys may be
present..

29. B+Trees are much easier and
higher performing to do a full
scan, as in look at every piece
of data that the tree indexes,
since the terminal nodes form
a linked list. To do a full scan
with a B-Tree you need to do a
full tree traversal to find all the
data.

30. Applications of B -Tree
A B-tree is a tree data structure
that keeps data sorted and
allows searches, insertions, and
deletions in logarithmic
amortized time.
Unlike self-balancing binary
search trees, it is optimized for
systems that read and write large
blocks of data. It is most
commonly used in database and
file systems.