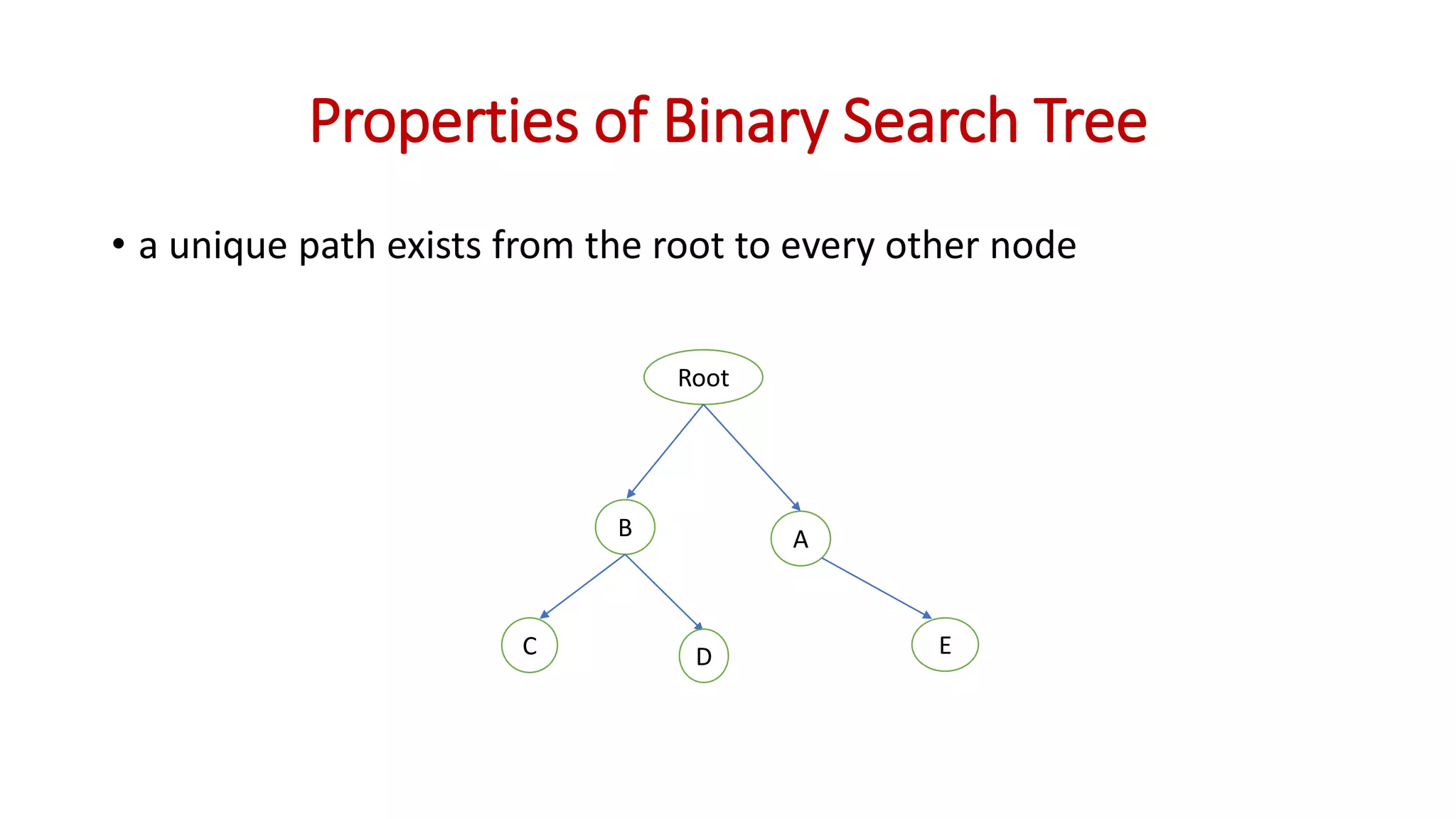
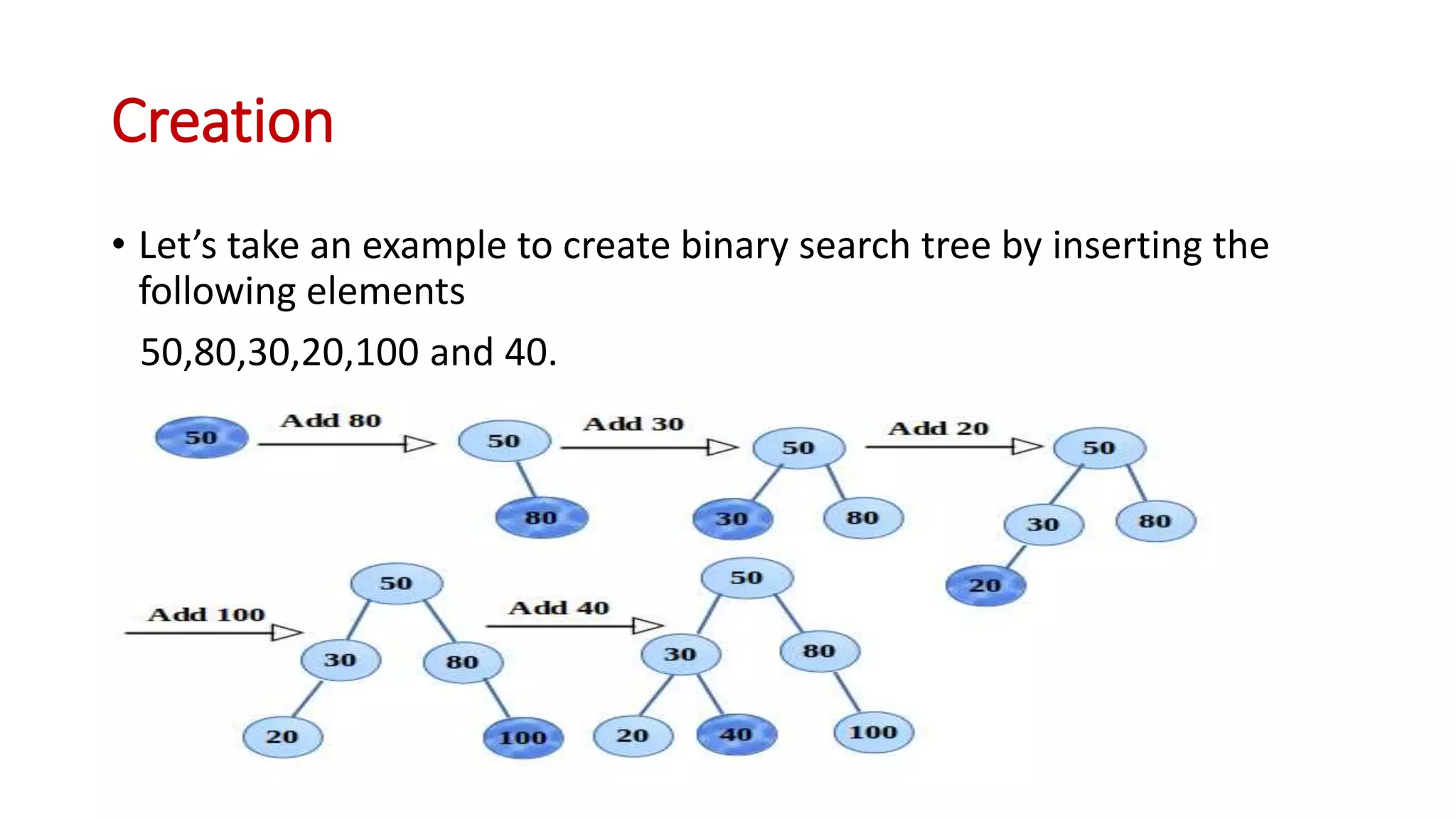
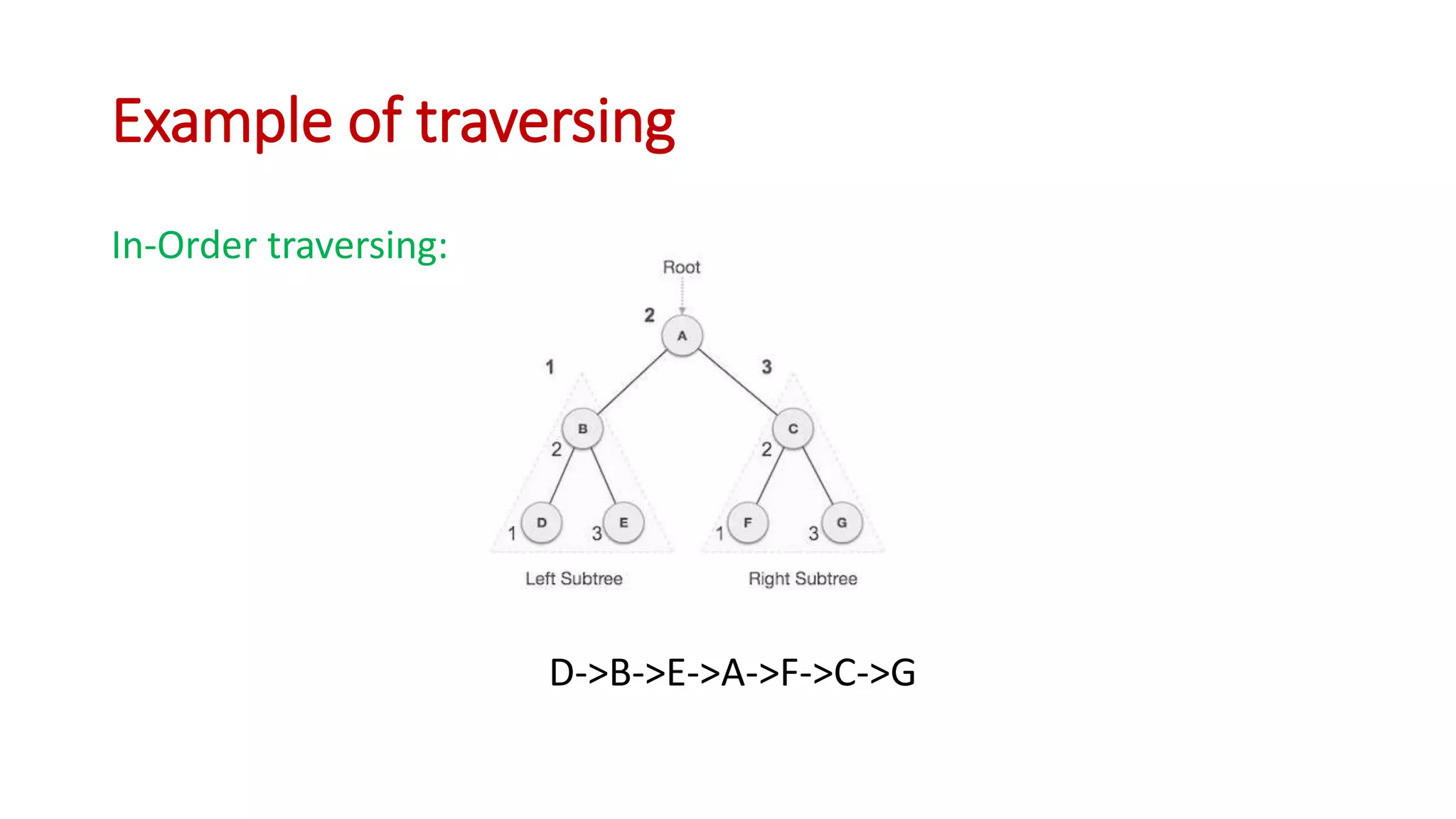
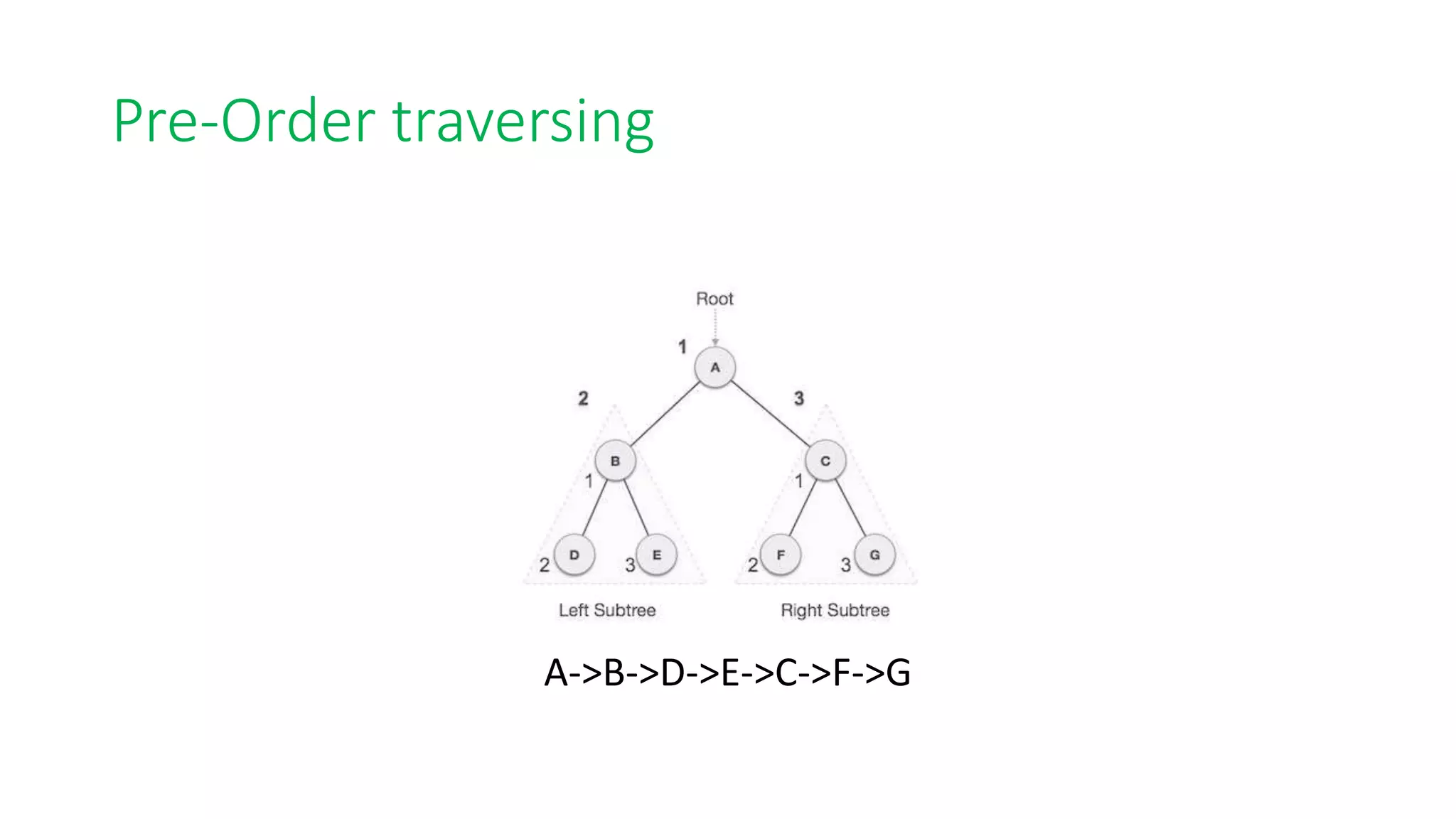
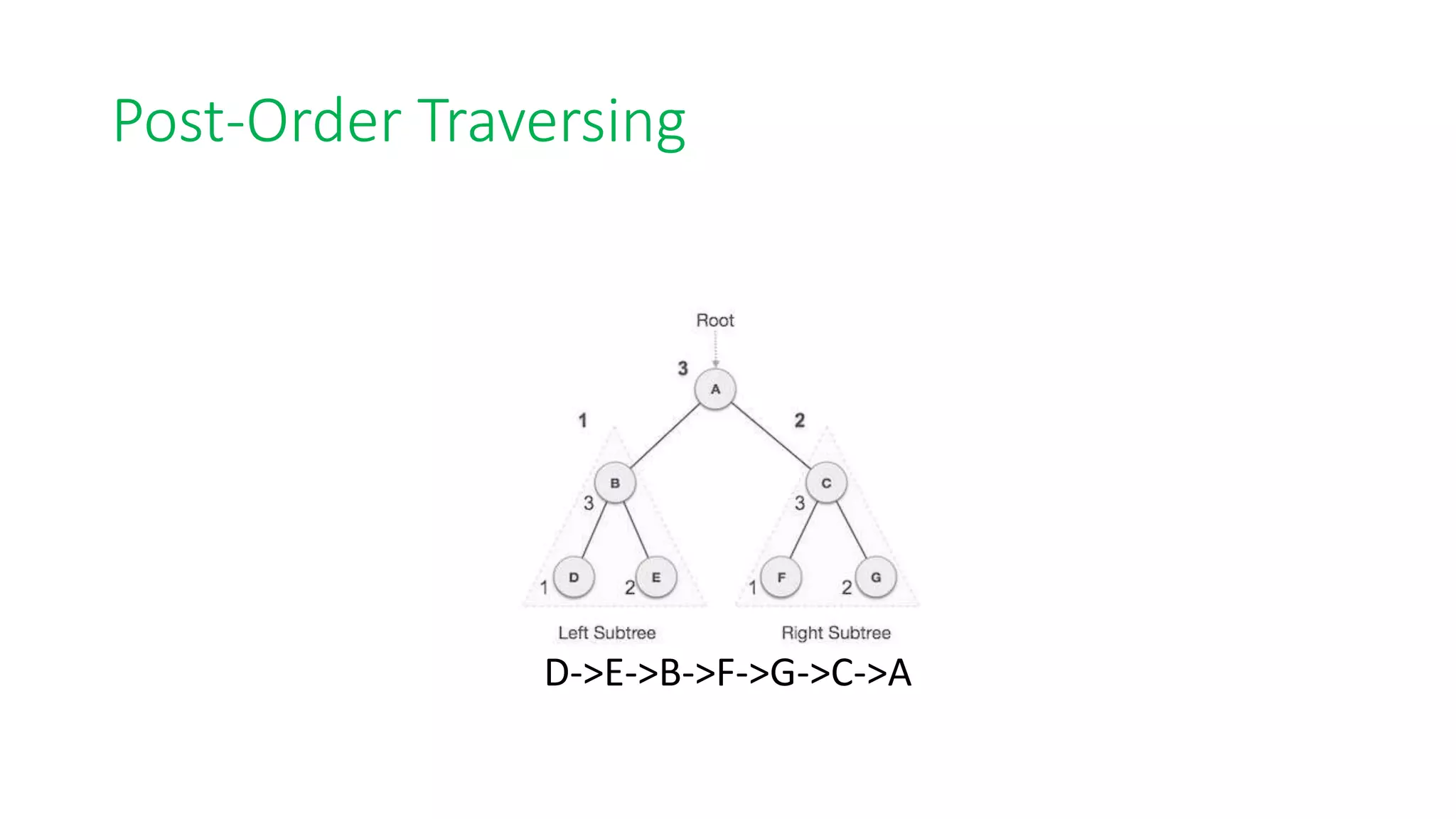
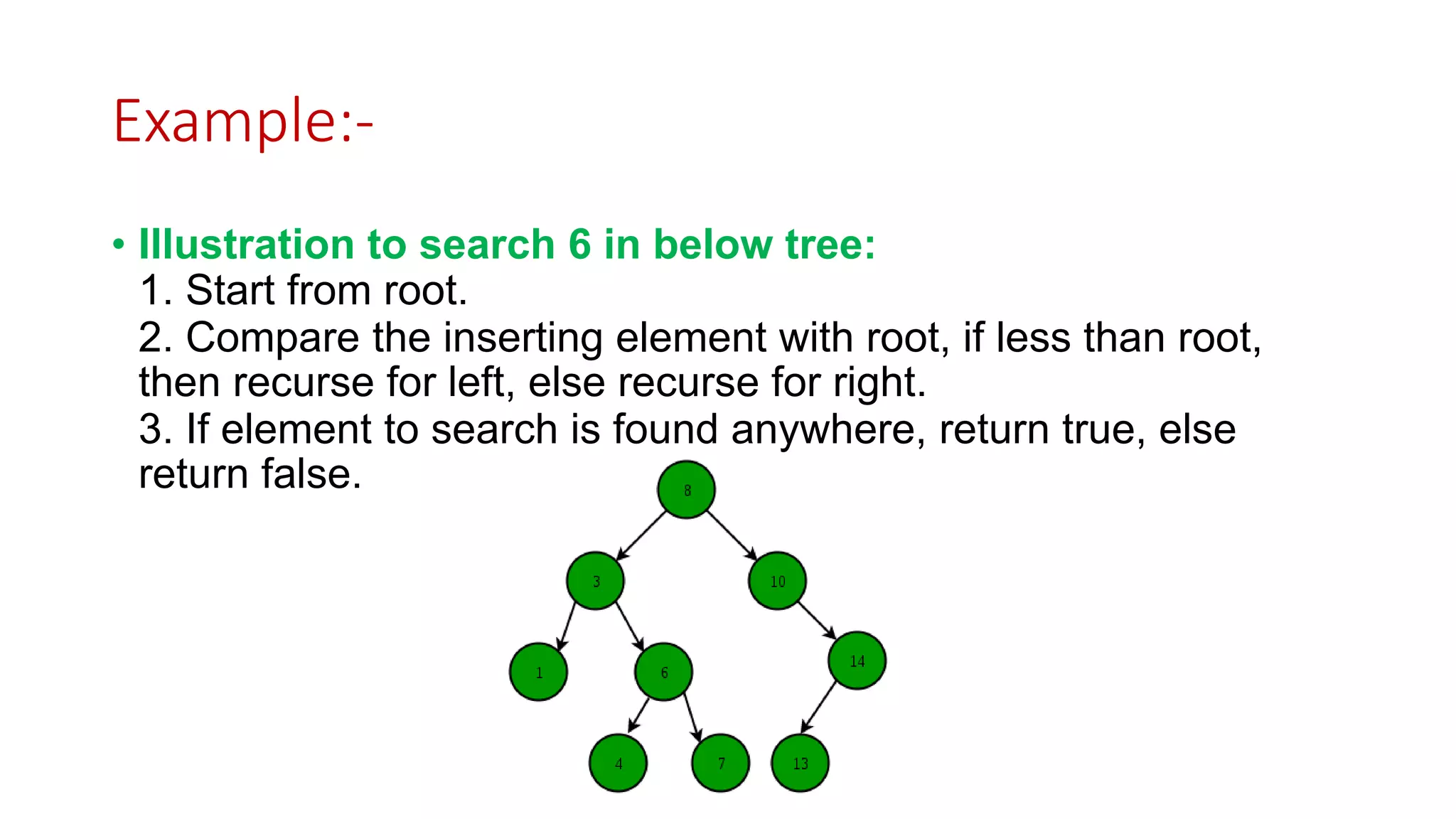
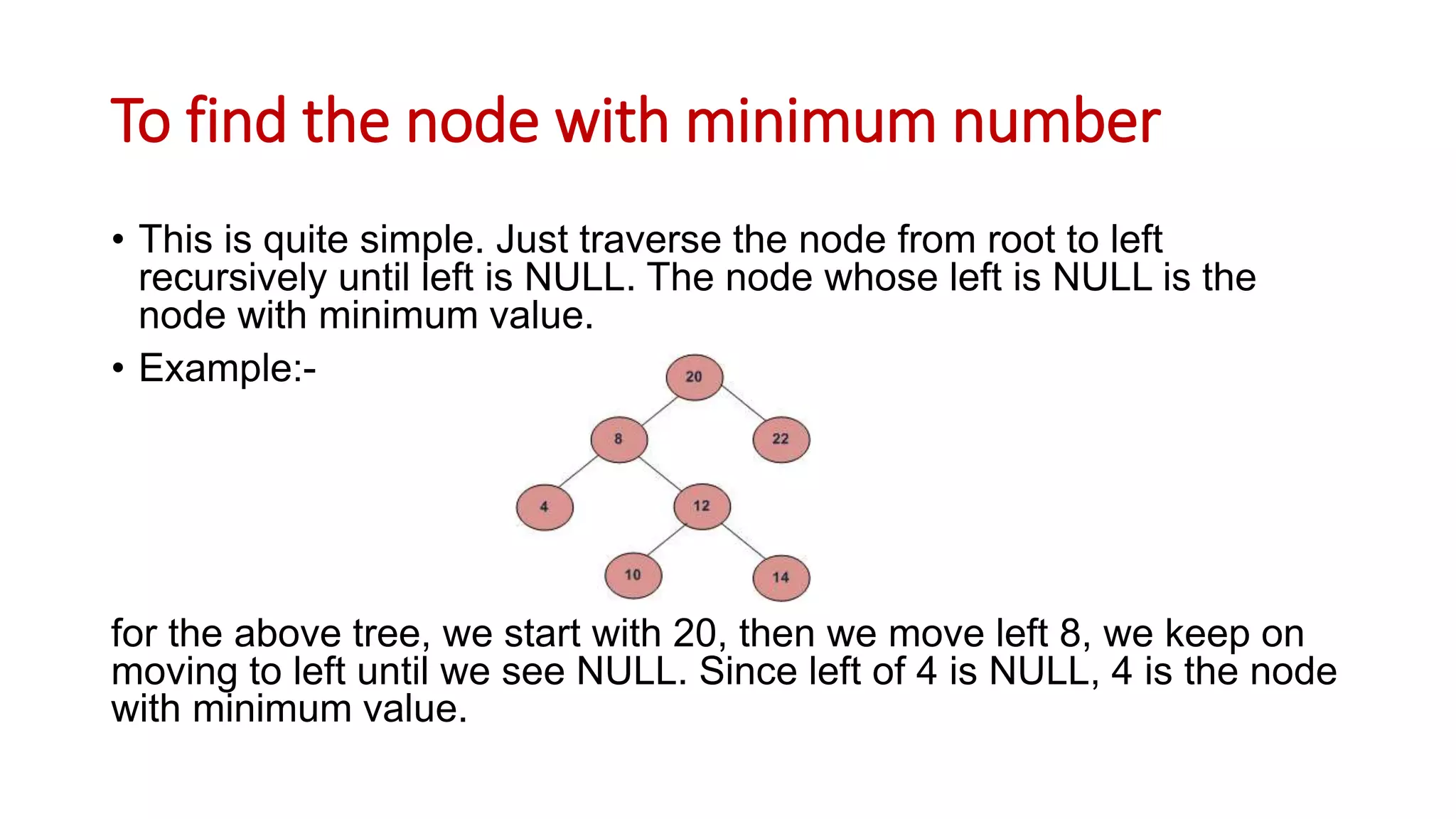
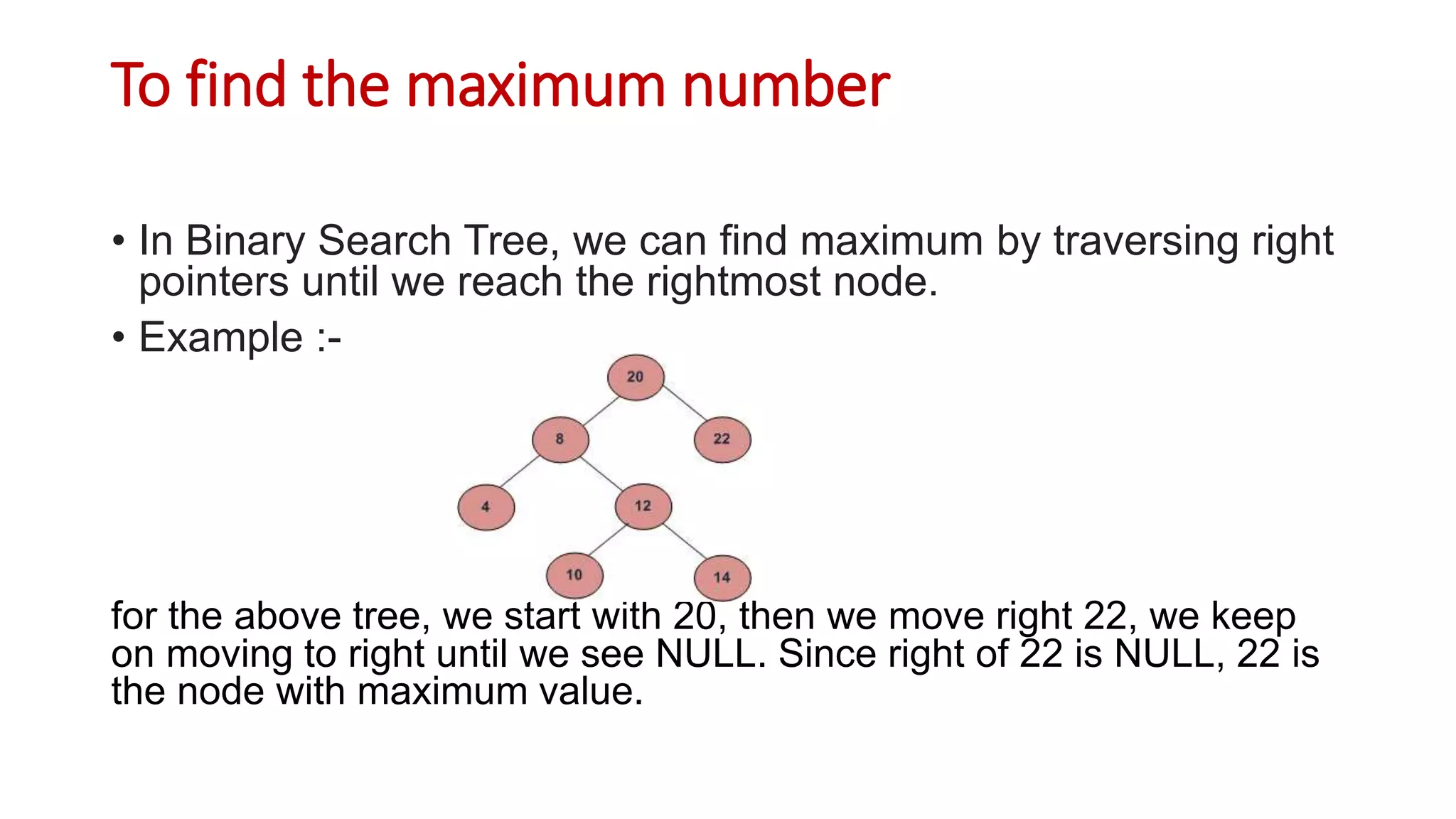
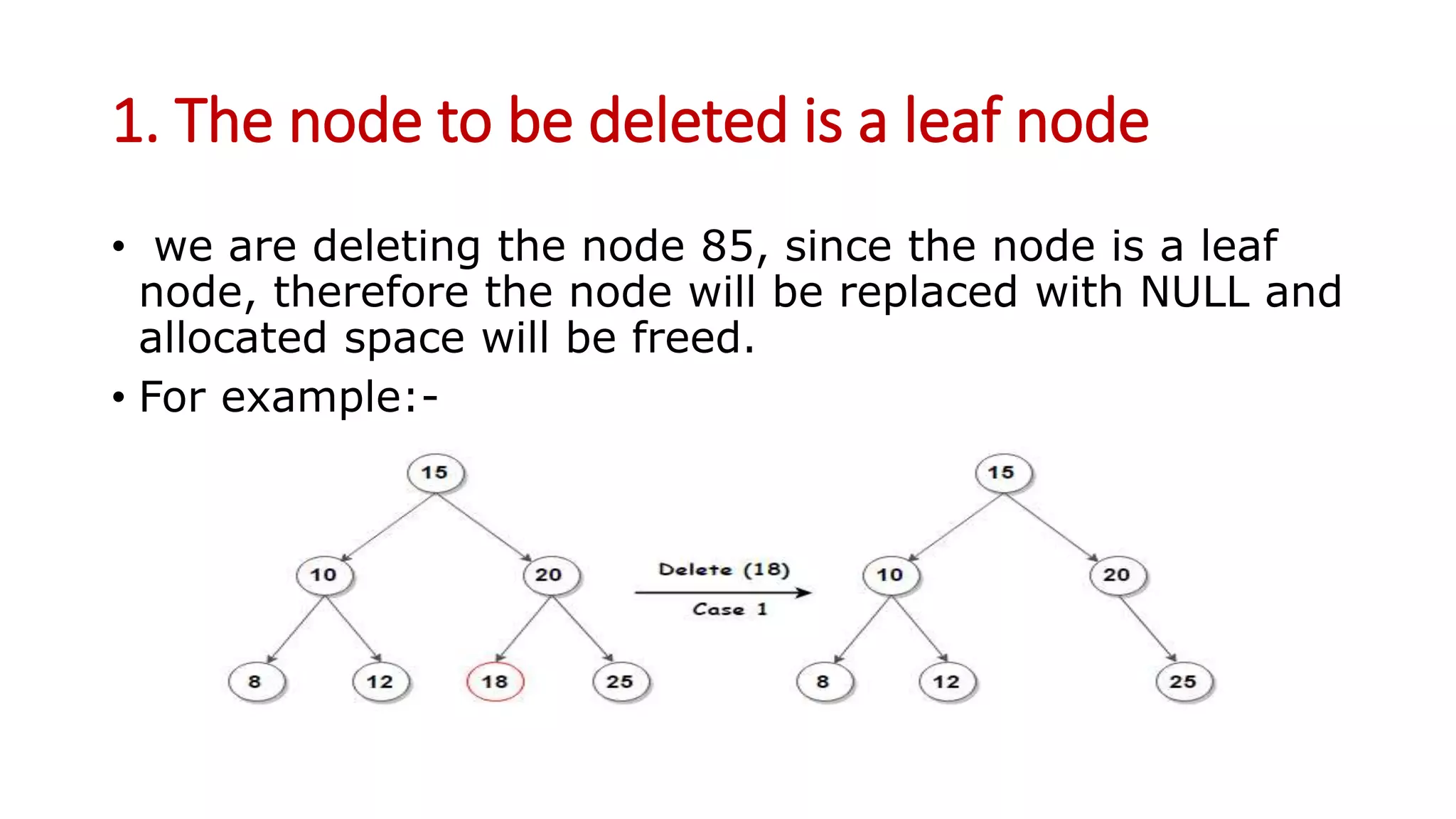
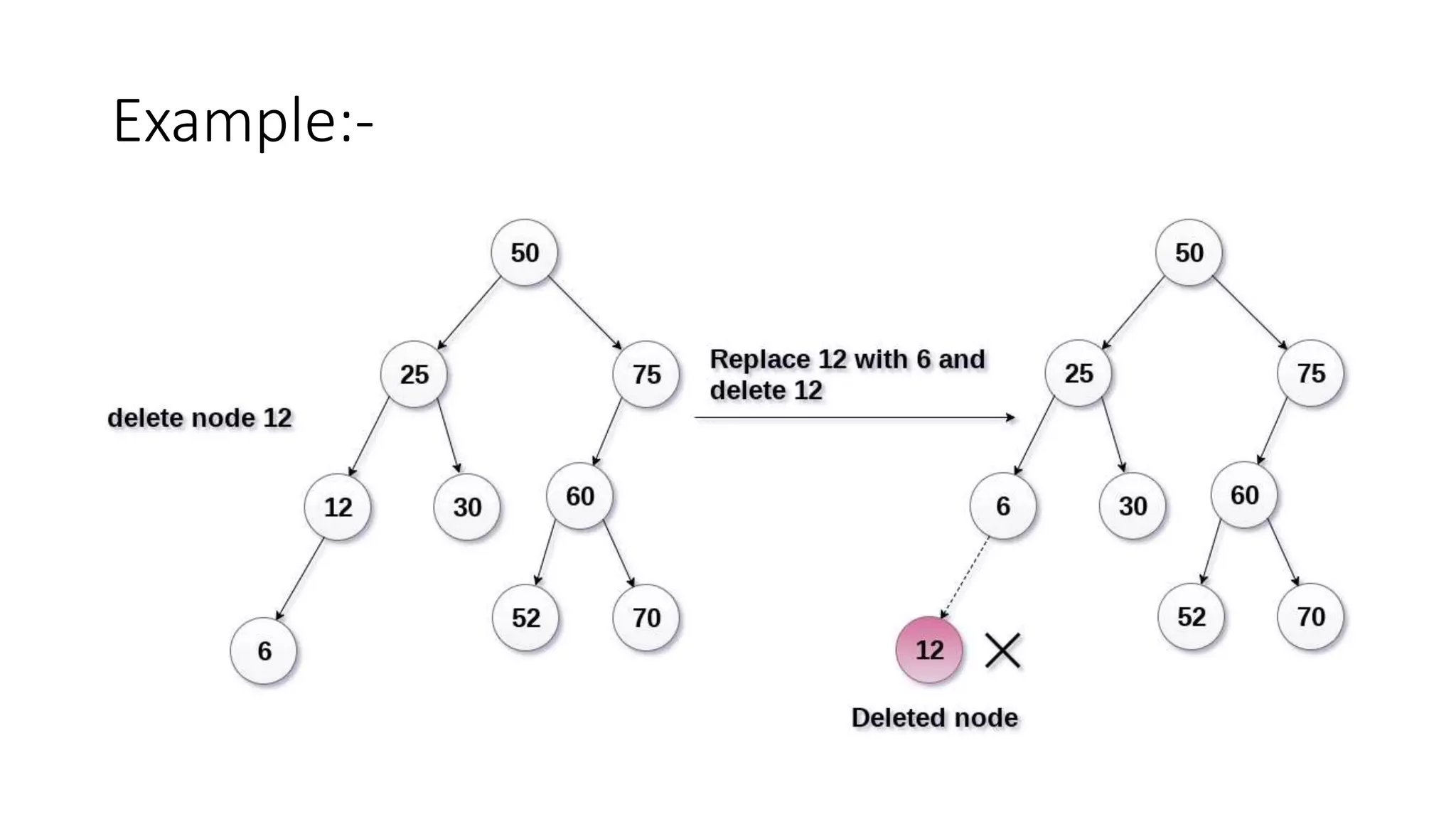
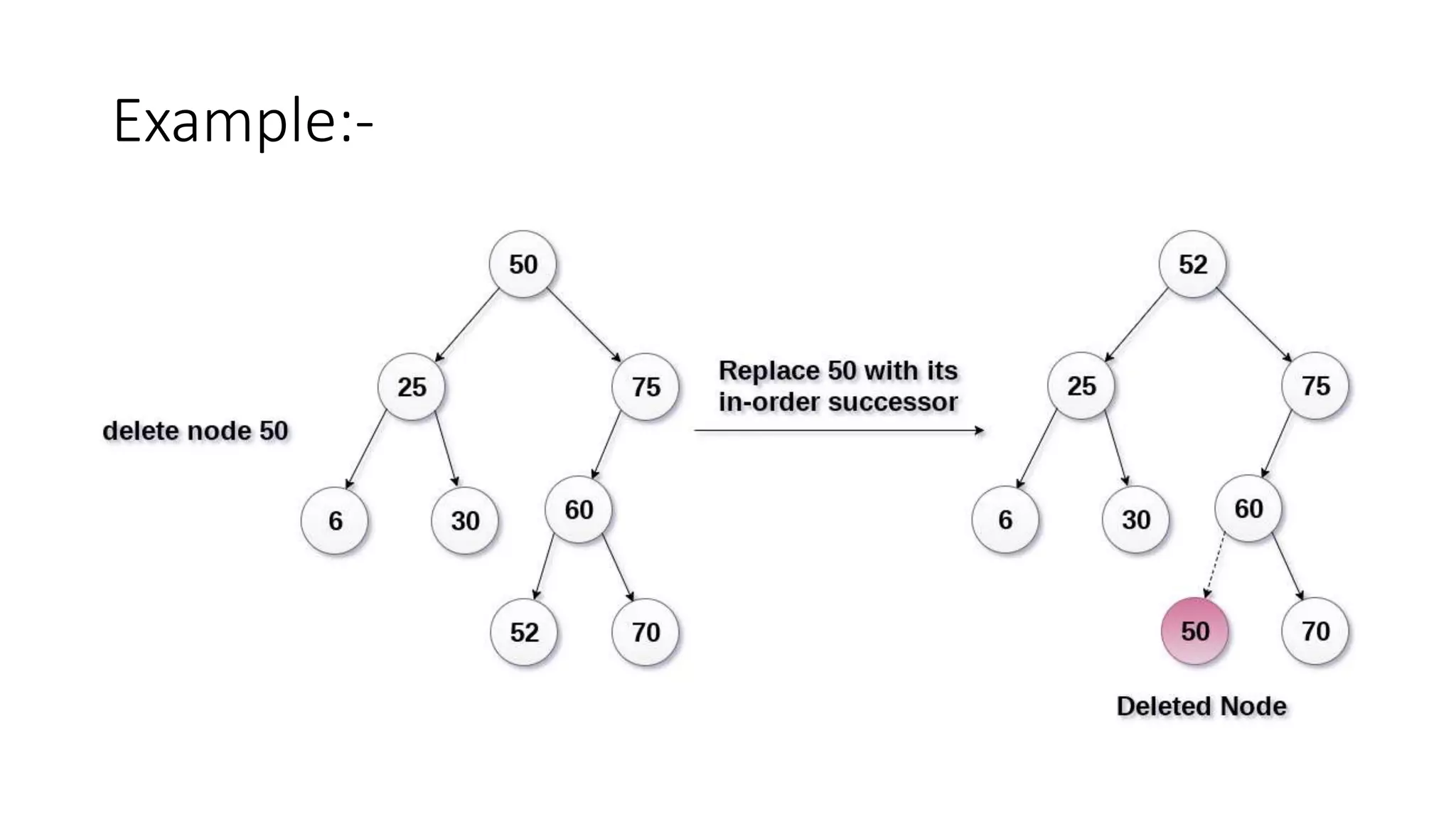
Binary search trees are binary trees where all left descendants of a node are less than the node's value and all right descendants are greater. This structure allows for efficient search, insertion, and deletion operations. The document provides definitions and examples of binary search tree properties and operations like creation, traversal, searching, insertion, deletion, and finding minimum and maximum values. Applications include dynamically maintaining a sorted dataset to enable efficient search, insertion, and deletion.

1. Binary Search Tree
Presented BY
Name-Sagar Yadav
Branch -B-tech (C.S.E)
Semester – 2
Enrollment No – A20405219144

2. What is binary search tree?
• Binary Search Tree is a binary tree in which every node contains only
smaller values in its left subtree and only larger values in its right
subtree.
• A Binary Search Tree (BST) is a rooted binary tree, whose nodes each
store a key (and optionally, an associated value) and each have two
distinguished sub-trees, commonly denoted left and right. The tree
should satisfy the BST property, which states that the key in each
node must be greater than all keys stored in the left sub-tree, and not
greater than all keys in the right sub-tree. Ideally, only unique values
should be present in the tree.

3. Properties of Binary Search Tree
• In a binary search tree, all the nodes in the left subtree of any node
contains smaller values and all the nodes in the right subtree of any
node contains larger values as shown in the following figure...

4. Properties of Binary Search Tree
• a unique path exists from the root to every other node
Root
AB
C D E

5. Basic Terminology
• The successor nodes of a node are called its children.
• The predecessor node of a node is called its parent.
• The "beginning" node is called the root (has no parent).
• A node without children is called a leaf.

6. Operations in Binary Search Tree
• The following basic operations are performed on a binary search tree.
1. Creation
2. Traversing
i. Pre-order
ii. Post-Order
iii. In-order
3. Search
4.insertion
5. Deletion
6.To find minimum number.
7. To find maximum number.

7. Creation
• Let’s take an example to create binary search tree by inserting the
following elements
50,80,30,20,100 and 40.

8. Function to create BST
node* create(node* root, int val)
{
node *temp,*base=root,*p,*q;
temp=(node*)malloc(sizeof(node));
temp->data=val;
temp->pre=NULL;
temp->next=NULL;
if(root==NULL) //to create root node
{
return temp;
}

9. else
{
p=q=root;
while(p!=NULL)
{
q=p;
if(p->data<temp->data)
p=p->next;
else
p=p->pre;
}
if(q->data<temp->data)
q->next=temp;
else
q->pre=temp;
}
return (base);
}

10. Traversing in Binary Search Tree
There are four ways to traverse the binary tree
1. In-order traversing :- It follow “Left Root Right”(LRoR)
rule. It always give result in ascending order.
2. Pre-order traversing:- It follow “Root Left Right”(RoLR)
rule. It always print root element in the starting.
3. Post-order traversing:- It follow “Left Right Root” (LRRo)
rule. It always print root element in the end

11. Example of traversing
In-Order traversing:
D->B->E->A->F->C->G

12. Pre-Order traversing
A->B->D->E->C->F->G

13. Post-Order Traversing
D->E->B->F->G->C->A

14. Function code to display the tree in In-Order
traversing
void inorder(node *temp) {
if (temp != NULL) {
inorder(temp->pre);
printf("%d", temp->data);
inorder(temp->next); // Using Recursion
}
}

15. Function code to display the tree in Pre-Order
Traversing
void preorder(node *temp) {
if (temp != NULL) {
printf("%d", temp->data);
preorder(temp->pre); //using recursion
preorder(temp->next); //using recursion
}
}

16. Function code to display the tree in Post-
Order
void postorder(node *temp) {
if (temp != NULL) {
postorder(temp->pre);
postorder(temp->next); //using recursion
printf("%d", temp->data); //using recursion
}
}

17. Searching in a Binary Search Tree
• To search a given key in Binary Search Tree, we first compare it
with root, if the key is present at root, we return root. If key is
greater than root’s key, we recur for right subtree of root node.
Otherwise we recur for left subtree.

18. Example:-
• Illustration to search 6 in below tree:
1. Start from root.
2. Compare the inserting element with root, if less than root,
then recurse for left, else recurse for right.
3. If element to search is found anywhere, return true, else
return false.

19. Function Code to search element in a given
tree using recursion
struct node* search(struct node* root, int key)
{
node *p;
if (root == NULL || root->data== key)// Base Cases: root is null or key is present at root
return root;
if (root->data < key){ // Key is greater than root's key
root=root->post;
return search(root, key);}
if(root->data>key){
root=root->pre;
return search(root, key); // Key is smaller than root's key
}

20. To find the node with minimum number
• This is quite simple. Just traverse the node from root to left
recursively until left is NULL. The node whose left is NULL is the
node with minimum value.
• Example:-
for the above tree, we start with 20, then we move left 8, we keep on
moving to left until we see NULL. Since left of 4 is NULL, 4 is the node
with minimum value.

21. Function code to find minimum number
Node* minimumKey(Node* root)
{
Node *p=root;
while(P->pre != NULL)
{
P = P->pre;
}
return p->data;
}

22. To find the maximum number
• In Binary Search Tree, we can find maximum by traversing right
pointers until we reach the rightmost node.
• Example :-
for the above tree, we start with 20, then we move right 22, we keep
on moving to right until we see NULL. Since right of 22 is NULL, 22 is
the node with maximum value.

23. Function code to find the maximum number
Node* maximumKey(Node* root)
{
Node *p=root;
while(P->post != NULL)
{
P = P->post;
}
return p->data;
}

24. Deletion in a Binary Search Tree
• Delete function is used to delete the specified node
from a binary search tree. However, we must delete a
node from a binary search tree in such a way, that the
property of binary search tree doesn't violate. There are
three situations of deleting a node from binary search
tree.

25. 1. The node to be deleted is a leaf node
• we are deleting the node 85, since the node is a leaf
node, therefore the node will be replaced with NULL and
allocated space will be freed.
• For example:-

26. 2. The node to be deleted has only one child
• In this case, replace the node with its child and delete
the child node, which now contains the value which is to
be deleted. Simply replace it with the NULL and free the
allocated space.

27. Example:-

28. 3. The node to be deleted has two child
• It is a bit complexed case compare to other two cases.
However, the node which is to be deleted, is replaced
with its in-order successor or predecessor recursively
until the node value (to be deleted) is placed on the leaf
of the tree. After the procedure, replace the node with
NULL and free the allocated space.

29. Example:-

30. Function code to delete element from a tree
node* deleteNode(struct node* root, int key)
{
node *temp;
if (root == NULL) return root; // base case
// If the key to be deleted is smaller than the root's key,
if (key < root->key) // then it lies in left subtree
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the root's key,
else if (key > root->key) // then it lies in right subtree
root->right = deleteNode(root->right, key);

31. // if key is same as root's key, then This is the node to be
deleted
else
{
// node with only one child or no child
if (root->left == NULL)
{
temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL)
{
temp = root->left;
free(root);
return temp;
}

32. // node with two children: Get the inorder successor (smallest in the right
subtree)
struct node* temp = minimumkey(root->right);
// Copy the inorder successor's content to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}

33. Applications of Binary Search Tree
• Binary search trees are collections that can efficiently maintain a
dynamically changing dataset in sorted order, for some "sortable"
type.*
• Having a sorted array is useful for many tasks because it enables
binary search to be used to efficiently locate elements. The problem
with a sorted array is that elements can't be inserted and removed
efficiently.
• The binary search tree is a different way of structuring data so that it
can still be binary searched (or a very similar procedure can be
used), but it's easier to add and remove elements. Instead of just
storing the elements contiguously from least to greatest, the data is
maintained in many separate chunks, making adding an element a
matter of adding a new chunk of memory and linking it to existing

34. Applications of Binary Search Tree
• Binary search trees support everything you can get from a sorted
array: efficient search, in-order forward/backwards traversal from any
given element, predecessor /successor element search, and max
/min queries, with the added benefit of efficient inserts and deletes.
With a self-balancing binary search tree (BST), all of the above run
in logarithmic time.
• It can store any type that has a total order defined on it. A total order
means a binary comparison operation between elements has been
defined, and the elements can be arranged in a unique sequence
from smallest to greatest based on this operation. For example,
integers or reals with the typical ("natural") order.