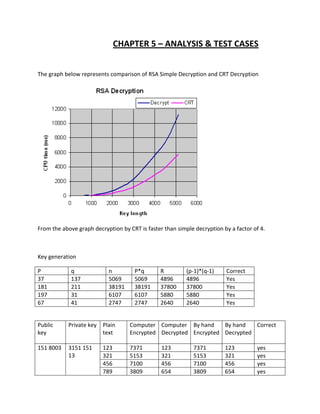
This document reports on a cryptanalysis project to analyze the RSA cryptosystem used in smartcards. It begins by introducing RSA and describing its key generation, encryption, and decryption processes. It then discusses three attacks that could be used against the smartcard RSA system: Fermat factorization, Wiener's continued fraction method, and the quadratic sieve algorithm. The document outlines the implementation details of these attacks and provides analysis of test cases. It concludes that the main goal is to find the secret key corresponding to a given 1024-bit public key and ciphertext.