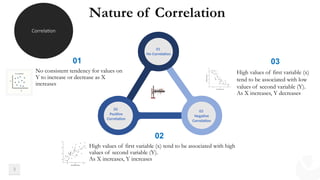
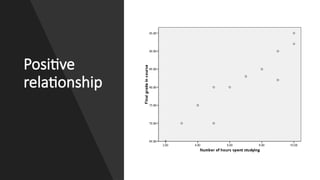
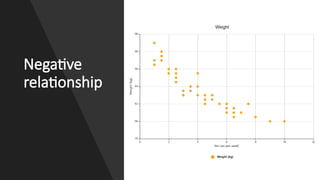
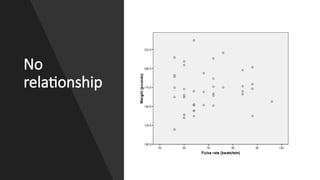
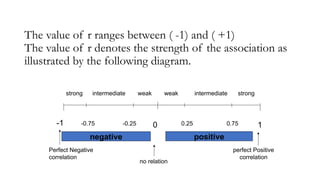
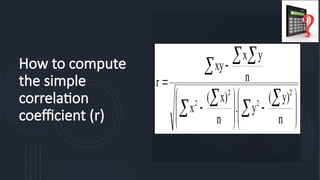
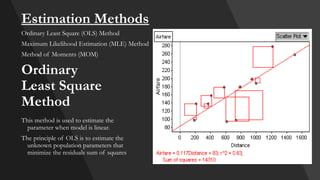
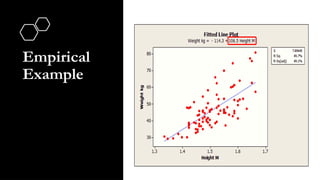
The document explains correlation and regression, highlighting correlation as a method to determine the linear relationship between two variables without inferring causation. It discusses the correlation coefficient, ranging from -1 to +1, which indicates the strength and nature of the relationship. Additionally, regression is introduced as a method to understand how changes in one variable affect another, distinguishing between independent and dependent variables.

1. Correlation
and
Regression

2. What is Correlation?
Finding the linear relationship between two
quantitative variables without being able to
infer causal relationships
Correlation is a statistical technique used to
determine the degree to which two variables
are related linearly

3. 3
Nature of Correlation
03
High values of first variable (x)
tend to be associated with low
values of second variable (Y).
As X increases, Y decreases
02
High values of first variable (x) tend to be associated with high
values of second variable (Y).
As X increases, Y increases
01
No Correlation
02
Positive
Correlation
01
No consistent tendency for values on
Y to increase or decrease as X
increases
Correlation
03
Negative
Correlation

4. Scatter plot
The pattern of data is indicative of the
type of relationship between two
variables:
positive relationship
negative relationship
no relationship

5. Positive
relationship

6. Negative
relationship

7. No
relationship

8. Correlation
Coefficient
Simple
Correlation
Coefficient (r)
Statistic showing the degree of
relation between two variables
It is also called Pearson's correlation
or product moment correlation
coefficient.
It measures the nature and strength
between two variables of
the quantitative type.

9. -1 1
0
-0.25
-0.75 0.75
0.25
strong strong
intermediate intermediate
weak weak
no relation
Perfect Negative
correlation
perfect Positive
correlation
positive
negative
The value of r ranges between ( -1) and ( +1)
The value of r denotes the strength of the association as
illustrated by the following diagram.

10. How to compute
the simple
correlation
coefficient (r) 



















 
 
  
n
y)
(
y
.
n
x)
(
x
n
y
x
xy
r
2
2
2
2

11. What is Regression?
In correlation, the two variables are treated as equals.
Regression tells how values in y change as a function of changes in values of x
In regression, one variable is considered independent (=predictor) variable (X) and the other
the dependent (=outcome) variable Y.
Regression may linear or non-linear
Linear Regression
In statistics, linear regression quantifies the relationship between one or more predictor
variable(s) and one outcome variable using linear equation
Mathematical expression used to describe the relationship between dependent variable and
one or more independent variables
Regression Model/Equation

12. Simple Linear Regression
Simple linear regression measure the relationship between one predictor variable(s) and one
outcome variable using linear equation
Population Regression Model
Where is dependent variable, is an independent variable, is called intercept, is called slope and is
error term
Sample Regression Model
Where is dependent variable, is an independent variable, is an estimator of , is an
estimator of and is the residual term

13. Ordinary
Least Square
Method
This method is used to estimate the
parameter when model is linear.
The principle of OLS is to estimate the
unknown population parameters that
minimize the residuals sum of squares
Estimation Methods
Ordinary Least Square (OLS) Method
Maximum Likelihood Estimation (MLE) Method
Method of Moments (MOM)

14. Mathematical Formulas of OLS estimators
Now we will perform empirical analysis in the excel

15. Empirical
Example

16. Thanks