Cone questões resolvidas - fundamentos de matemática elementar

QUESTÕES RESOLVIDAS DO LIVRO: FUNDAMENTOS DE
MATEMÁTICA ELEMENTA, VOL. 10
Assunto: Cones

Geometria Espacial – Celso do Rozário Brasil 1
CONE – EXERCÍCIOS RESOLVIDOS
Celso do Rozário Brasil
RESOLUÇÕES DE QUESTÕES SOBRE CONES DO LIVRO: FUNDAMENTOS DE MATEMÁTICA ELEMENTAR,
VOLUME 10
(Fundamentos de Matemática Elementar, FME, Vol. 10, p. 241, questão 593) - Determine a medida da altura
de um cone cuja geratriz mede 10 cm, sendo 12 cm o diâmetro de sua base.
Solução
(FME, questão 594) Determine a medida do diâmetro da base de um cone de revolução cuja geratriz mede
65 cm, sendo 56 cm a altura do cone.
Solução
(FME, questão 595) Calcule a medida da altura de um cone de raio “r”, sabendo que sua base é equivalente
à secção meridiana.
Solução
Devemos ter:
(i) No triângulo retângulo VOA destacado, temos:
10² = h² + 6² ---->
100 = h² + 36 ---->
h² = 100 – 36 ---->
h² = 64 ---->
h = √64
h = 8 cm
(i) No triângulo retângulo VOA, por Pitágoras, temos:
(65)2
= (56)2
+ 𝑟2
→ 4225 = 3136 + 𝑟2
→ 𝑟2
= 1089 →
𝑟 = √1089 → 𝒓 = 𝟑𝟑
(ii) Logo, o diâmetro da base do cone vale:
D = 2r ----> D = 2.33 -----> D = 66 cm

(FME, questão 596) Determine a medida do raio da base de um cone de revolução cuja altura mede 3 cm e
cujo volume é 9𝜋 cm³.
Solução
r = ?
h = 3 cm
V = 9π →
πr2
h
3
= 9π → r2
. 3 = 27 → r2
= 9 → 𝐫 = 𝟑 𝐜𝐦
(FME, questão 597) Determine a medida do raio da base de um cone de revolução de altura 3 cm, sendo
16𝜋 cm³ o seu volume.
Solução
r = ?
h = 3 cm
V = 16π →
πr2
h
3
= 16π → r2
. 3. = 48 → r2
= 16 → r = √16 → 𝐫 = 𝟒 𝐜𝐦
(FME – Questão 598) Um cone equilátero tem raio da base “r”. Calcule:
(a) A área lateral;
(b) A medida em radianos do ângulo do setor circular equivalente à superfície lateral;
(c) A área total;
(d) O volume.
Solução
(i) Área da base: 𝐒𝐛 = 𝛑𝐫²
(ii) Área da secção meridiana:
Ssm =
2r. h
2
→ 𝐒𝐬𝐦 = 𝐫. 𝐡
(iii) Como a base é equivalente à secção meridiana,
devemos ter suas respectivas áreas iguais:
Sb = Ssm → πr2
= r. h → 𝐡 = 𝛑𝐫
(i) A secção meridiana de um cone equilátero é um
triângulo equilátero, logo, sua altura é igual a
altura do cone:
(2r)² = h² + r² ----> 4r² = h² + r² ----> h² = 4r²-r² --->
h² = 3r² ----> h = √3r² → 𝐡 = 𝐫√𝟑

(a) Cálculo da área lateral:
SL = πrg → SL = πr. 2r → 𝐒𝐋 = 𝟐𝛑𝐫²
(b) ângulo do setor circular:
θ =
2πr
g
→ θ =
2πr
2r
→ 𝛉 = 𝛑 𝐫𝐚𝐝
(c) Cálculo da área total:
ST = SL + Sb → ST = 2πr2
+ πr² → 𝐒𝐓 = 𝟑𝛑𝐫²
(d) Cálculo do volume:
V =
πr2
h
3
→ V =
πr2
. r√3
3
→ 𝐕 =
√𝟑
𝟑
𝛑𝐫³
(FME – Questão 599) Calcule o raio e a altura de um cone de revolução cujo desenvolvimento é um semicírculo
de raio “a”.
(FME – Questão 600) A geratriz de um cone mede 14 cm e a área da base 𝟖𝟎𝛑 cm². Calcule a medida da altura
do cone.
Solução
g = 14 cm
Sb = 80π → πr2
= 80π → 𝐫𝟐
= 𝟖𝟎
Sendo:
𝑔2
= 𝑟2
+ ℎ2
→ (14)2
= 80 + ℎ2
→ ℎ2
= 196 − 80 → ℎ2
= 116 → ℎ = √116 → ℎ = √22. 29 →
(i) Considerando g = “a”. Sabemos que o ângulo 𝛉 é dado por:
θ =
2πr
a
→ 2πr = θ. a → r =
θa
2π
→ Fazendo θ = π, temos:
r =
πa
2π
→ 𝐫 =
𝐚
𝟐
(ii) Sendo: g² = r² + h², temos:
a2
= r2
+ h2
→ a2
= (
a
2
)
2
+ h2
→ a2
= (
a2
4
) + h2
→
h2
= a2
−
a2
4
→ h2
=
3a2
4
→ h = √
3a2
4
→ 𝐡 =
√𝟑
𝟐
𝐚

𝐡 = 𝟐√𝟐𝟗 𝐜𝐦
(FME – Questão 601) Determine a medida da área lateral de um cone equilátero, sendo 20 cm a medida da
sua geratriz.
Solução
g = 20 cm
(i) A altura do cone equilátero é dada por:
h = r√3
(ii) Sabemos que:
g2
= r2
+ h2
→ (20)2
= r2
+ (r√3)
2
→ 400 = r2
+ 3r2
→ 4r2
= 400 ÷ 4 → 𝐫𝟐
= 𝟏𝟎𝟎 → r = √100 →
𝐫 = 𝟏𝟎 𝐜𝐦
(iii) A área lateral do cone equilátero é dada por:
SL = 2πr2
→ SL = 2π. 100 → 𝐒𝐋 = 𝟐𝟎𝟎𝛑 𝐜𝐦²
(FME – Questão 602) Determine a área total de um cone, cuja secção meridiana é um triângulo equilátero de
8 dm de lado.
Solução
(FME – Questão 603) Determine a medida da área lateral e da área total de um cone de revolução, sabendo
que sua altura mede 12 cm e sua geratriz 13 cm.
Solução
h = 12 cm
g = 13 cm
g2
= h2
+ r2
→ (13)2
= (12)2
+ r2
→ 169 = 144 + r2
→ r2
= 169 − 144 → r2
= 25 → 𝐫 = 𝟓 𝐜𝐦
(i) Cálculo da área lateral:
SL = πrg → SL = π. 5.13 → 𝐒𝐋 = 𝟔𝟓𝛑 𝐜𝐦²
(i) No triângulo retângulo destacado ao lado, temos:
82
= h2
+ 42
→ 64 = h2
+ 16 → h2
= 48 → h = √48 →
h = √22. 22. 3 → 𝐡 = 𝟒√𝟑 𝐝𝐦
(ii) Pela figura, notamos que o raio do cone vale: 4 dm.
(iii) A área total do cone equilátero é dada por:
ST = 3πr2
→ ST = 3π. 42
→ ST = 3.16π → 𝐒𝐓 = 𝟒𝟖𝛑 𝐝𝐦²

(ii) Cálculo da área total:
ST = SL + Sb → ST = πrg + πr2
→ ST = πr(g + r) → ST = π. 5(13 + 5) → ST = 5π. 18 → ST = 90π cm²
(FME – Questão 604) Determine a medida da altura de um cone equilátero cuja área total mede 𝟓𝟒𝝅 cm².
Solução
(i) ST = SL + Sb → ST = 2πr2
+ πr2
→ ST = 3πr2
→ 54π = 3πr2
→ r2
= 18 → 𝐫 = 𝟑√𝟐
A secção meridiana do cone equilátero é um triângulo equilátero cujo lado vale: L = 2r ----> L = 6√2
(ii) A altura do cone equilátero é dada por:
h =
L√3
2
→ h =
6√2. √3
2
→ h =
6√6
2
→ 𝐡 = 𝟑√𝟔 𝐜𝐦
(FME – Questão 605) Calcule a área total e o volume de um cone equilátero, sabendo que a área lateral é
igual a 𝟐𝟒𝝅 cm².
Solução
SL = πrg → SL = πr. 2r → 𝐒𝐋 = 𝟐𝛑𝐫𝟐
→ 24π = 2πr2
→ 2r2
= 24r → 𝐫𝟐
= 𝟏𝟐 → 𝐫 = √𝟏𝟐 𝐜𝐦
(i) Cálculo da área total:
ST = 3πr2
→ ST = 3π. 12 → 𝐒𝐓 = 𝟑𝟔𝛑 𝐜𝐦²
(ii) Cálculo do volume:
V =
πr2
h
3
→ V =
πr2
. r√3
3
→ 𝐕 =
√𝟑
𝟑
𝛑𝐫𝟑
→ V =
√3
3
𝜋. (√12)
3
→ V =
√3
3
𝜋. [(√12)
2
(√12)] →
V =
√3
3
π. 12. √12 → V = √3π. 4.2√3 → V = 8. .3π → 𝐕 = 𝟐𝟒𝛑 𝐜𝐦³
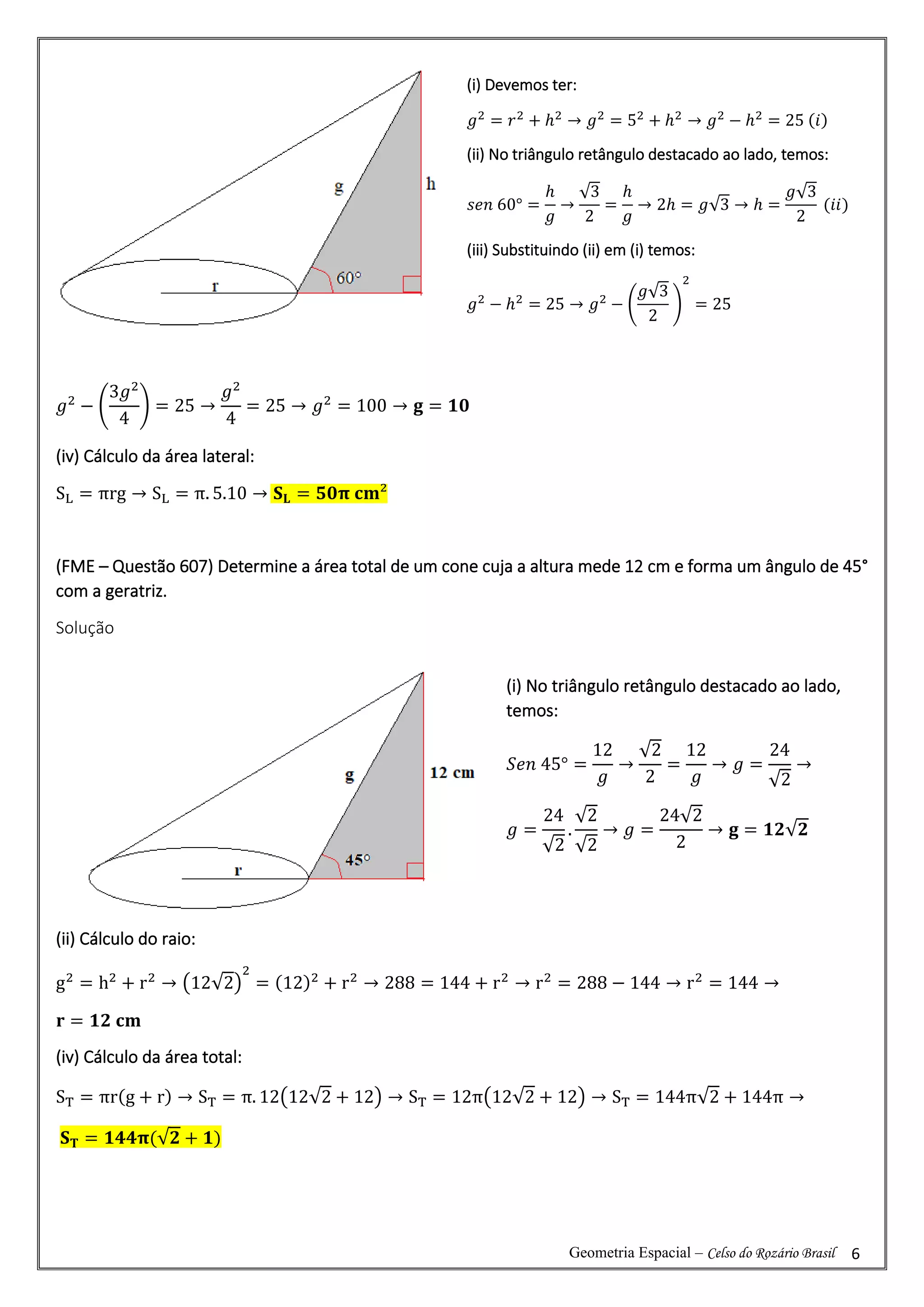
(FME – Questão 606) Determine a área lateral de um cone cujo raio da base mede 5 cm, sendo 60° o ângulo
que a geratriz forma com a base do cone.
Solução

𝑔2
− (
3𝑔2
4
) = 25 →
𝑔2
4
= 25 → 𝑔2
= 100 → 𝐠 = 𝟏𝟎
(iv) Cálculo da área lateral:
SL = πrg → SL = π. 5.10 → 𝐒𝐋 = 𝟓𝟎𝛑 𝐜𝐦²
(FME – Questão 607) Determine a área total de um cone cuja a altura mede 12 cm e forma um ângulo de 45°
com a geratriz.
Solução
(ii) Cálculo do raio:
g2
= h2
+ r2
→ (12√2)
2
= (12)2
+ r2
→ 288 = 144 + r2
→ r2
= 288 − 144 → r2
= 144 →
𝐫 = 𝟏𝟐 𝐜𝐦
(iv) Cálculo da área total:
ST = πr(g + r) → ST = π. 12(12√2 + 12) → ST = 12π(12√2 + 12) → ST = 144π√2 + 144π →
𝐒𝐓 = 𝟏𝟒𝟒𝛑(√𝟐 + 𝟏)
(i) Devemos ter:
𝑔2
= 𝑟2
+ ℎ2
→ 𝑔2
= 52
+ ℎ2
→ 𝑔2
− ℎ2
= 25 (𝑖)
(ii) No triângulo retângulo destacado ao lado, temos:
𝑠𝑒𝑛 60° =
ℎ
𝑔
→
√3
2
=
ℎ
𝑔
→ 2ℎ = 𝑔√3 → ℎ =
𝑔√3
2
(𝑖𝑖)
(iii) Substituindo (ii) em (i) temos:
𝑔2
− ℎ2
= 25 → 𝑔2
− (
𝑔√3
2
)
2
= 25
(i) No triângulo retângulo destacado ao lado,
temos:
𝑆𝑒𝑛 45° =
12
𝑔
→
√2
2
=
12
𝑔
→ 𝑔 =
24
√2
→
𝑔 =
24
√2
.
√2
√2
→ 𝑔 =
24√2
2
→ 𝐠 = 𝟏𝟐√𝟐

(FME – Questão 608) O raio da base de um cone mede 12 cm. Sabendo que a altura forma um ângulo de 60°
com a geratriz do cone, determine a sua área lateral.
Solução
(iii) Cálculo da área lateral:
SL = πrg → SL = π. 12.24 → 𝐒𝐋 = 𝟐𝟖𝟖𝛑 𝐜𝐦𝟐
(FME – Questão 609) A geratriz de um cone de revolução forma com o eixo do cone um ângulo de 45°. Sendo
A, a área da secção meridiana do cone, calcule sua área total.
Solução
(iv) Cálculo da área total:
ST = πr(g + r) → ST = πr(r√2 + r) → ST = πr²√2 + πr² → ST = πr²(√2 + 1) → 𝐒𝐓 = 𝛑(√𝟐 + 𝟏)𝐀
(i) No triângulo retângulo destacado ao lado, temos:
Se𝐧 𝟔𝟎° =
𝐡
𝐠
→
√𝟑
𝟐
=
𝐡
𝐠
→ 𝟐𝐡 = 𝐠√𝟑 → 𝐡 =
𝐠√𝟑
𝟐
(ii) Sabemos que:
g2
= r2
+ h2
→ g2
= (12)2
+ (
g√3
2
)
2
→
g2
= 144 +
3g2
4
→ g² =
576 + 3g2
4
→
4g2
− 3g2
= 576 → g2
= 576 → g = √576 →
𝒈 = 𝟐𝟒 𝒄𝒎
(i) Note que o triângulo retângulo VOA destacado é isósceles, logo:
h = r
(ii) Ainda no triângulo VOA, temos que a área da secção meridiana é:
ASM =
2r. h
2
→ ASM = ASM = r. h → ASM = r. r → 𝐀𝐒𝐌 = 𝐫𝟐
𝒐𝒖
𝑨 = 𝒓²
(iii) Sabemos que:
𝑔2
= 𝑟2
+ ℎ2
→ 𝑔2
= 𝑟2
+ 𝑟2
→ 𝑔2
= 2𝑟2
→ 𝐠 = 𝐫√𝟐
Sen 45° =
h
g
→
√2
2
=
h
g
→ 2h = g√2 →

(FME – Questão 610) A planificação da superfície lateral de um cone de revolução é um setor circular de 90°.
Calcule a razão entre o raio da base do cone e a geratriz do cone.
Solução
(FME – Questão 611) Determine a razão entre o raio da base e a geratriz de um cone de revolução, sabendo
que o desenvolvimento da superfície lateral é um setor circular cujo ângulo mede 60°.
Solução
(FME – Questão 612) Determine a altura de um cone, sabendo que o desenvolvimento de sua superfície
lateral é um setor circular de 135° e raio igual a 10 cm.
Solução
(i) O ângulo do setor circular é dado por:
θ =
2πr
g
→ 135° =
360°. 10
g
→ g =
3600
135
:
5
5
→ g =
720
27
:
9
9
→ 𝐠 =
𝟖𝟎
𝟑
(ii) Cálculo da altura:
g2
= r2
+ h2
→ (
80
3
)
2
= (10)2
+ h2
→
6400
9
= 100 + h2
→ h2
=
6400
9
− 100 → h² =
6400 − 900
9
→
ℎ2
=
5500
9
→ ℎ = √
55.100
9
→ 𝐡 =
𝟏𝟎
𝟑
√𝟓𝟓 𝐜𝐦
(FME – Questão 613) Determine o ângulo central (em graus) de um setor circular obtido pelo
desenvolvimento da superfície lateral de um cone cuja geratriz mede 18 cm e o raio da base 3 cm.
O ângulo do setor circular é:
𝜃 =
2πr
𝑔
→ 𝜃 =
360. 𝑟
𝑔
→ 𝜃 =
𝑟
𝑔
. 360° →
𝑟
𝑔
=
𝜃
360°
→
𝑟
𝑔
=
90°
360°
→
𝐫
𝐠
=
𝟏
𝟒
O ângulo do setor circular é:
θ =
2πr
g
→ θ =
360. r
g
→ θ =
r
g
. 360° →
r
g
=
θ
360°
→
r
g
=
60°
360°
→
𝐫
𝐠
=
𝟏
𝟔

Solução
θ =
2πr
g
→ θ =
2π. 3
18
→ θ =
6π
18
:
6
6
→ θ =
π
3
→ θ =
180°
3
→ 𝛉 = 𝟔𝟎°
(FME – Questão 614) Determine a medida (em graus) do ângulo do setor circular resultante do
desenvolvimento sobre um plano da superfície lateral de um cone cuja altura e cujo raio estão na razão 3/4.
Solução
(i)
h
r
=
3
4
→ 4h = 3r → 𝐡 =
𝟑𝐫
𝟒
(ii) g2
= h2
+ r2
→ g2
= (
3r
4
)
2
+ r2
→ g2
=
9r2
16
+ r2
→ g2
=
9r2+16r2
16
→ g2
=
25r2
16
→ g =
√
25r2
16
→ 𝐠 =
𝟓𝐫
𝟒
θ =
2πr
g
→ θ =
360°. r
5r
4
→ θ =
360.4
5
→ θ = 72.4 → 𝛉 = 𝟐𝟖𝟖°
(FME – Questão 615) A área da base de um cone de revolução é 1/3 da área total. Calcule o ângulo (em graus)
do setor circular que é o desenvolvimento da superfície lateral do cone.
Solução
(i) Devemos ter:
Sb =
1
3
ST → πr2
=
1
3
. πr(g + r) → r =
1
3
. (g + r) → 3r = g + r → 3r − r = g → 𝐠 = 𝟐𝐫
(ii) ângulo do setor circular:
θ =
2πr
g
→ θ =
2π. r
2r
→ θ = π → 𝛉 = 𝟏𝟖𝟎°
(FME – Questão 616) O diâmetro da base de um cone circular reto mede 3 m e a área da base é 2/5 da área
total. Calcule o ângulo (em graus) do setor circular que é o desenvolvimento da superfície lateral do cone.
Solução
(i) Diâmetro da base = 3 m -----> Raio da base r= 3/2 m
(ii) Sb =
2
5
ST → πr2
=
2
5
πr(g + r) → r =
2
5
(g + r) → 5r = 2g + 2r → 5r − 2r = 2g → 3r = 2g →
g =
3.
3
2
2
→ 𝐠 =
𝟗
𝟒
(ii) ângulo do setor circular:
θ =
2πr
g
→ θ =
2π.
3
2
9
4
→ θ =
3π
9
4
→ θ = 3π.
4
9
→ θ =
4π
3
→ θ =
4.180
3
→ θ = 4.60 → 𝛉 = 𝟐𝟒𝟎°

(FME – Questão 617) Determine a área total de um cone, sendo 40 cm o diâmetro de sua base e 420 cm² a
área de sua secção meridiana.
Solução
(i) Diâmetro da base = 40 cm -----> Raio da base r= 20 cm
(ii) Na secção meridiana a base do triângulo isósceles é igual ao diâmetro da base: b = 40 cm
SSM = 420 → SSM =
b. h
2
→
40. h
2
= 420 → 20h = 420 → h =
42
2
→ 𝐡 = 𝟐𝟏 𝐜𝐦
(iii) Cálculo da geratriz:
g2
= h2
+ r2
→ g2
= (21)2
+ (20)2
→ g2
= 441 + 400 → g2
= 841 → g = √841 → 𝐠 = 𝟐𝟗 𝐜𝐦
(iii) Cálculo da área total:
ST = πr(g + r) → ST = π. 20(29 + 20) → ST = 20π. 49 → 𝐒𝐓 = 𝟗𝟖𝟎𝛑 𝐜𝐦²
(FME – Questão 618) Determine a superfície lateral de um cone cuja área da base mede 𝟔, 𝟐𝟓𝝅 𝒄𝒎², sendo
4 cm a medida da sua altura.
Solução
Altura: h = 4 cm
(i) Sb = 6,25π → πr2
= 6,25π → r2
= 6,25 → r = √6,25 → 𝐫 = 𝟐, 𝟓 𝐜𝐦
(ii) Cálculo da geratriz:
g2
= h2
+ r2
→ g2
= 42
+ (2,5)2
→ g2
= 16 + 6,25 → g2
= 22,25 → 𝐠 = √𝟐𝟐, 𝟐𝟓 𝐜𝐦
SL = πrg → SL = π. 2,5. √22,25 → 𝐒𝐋 = 𝟐, 𝟓𝛑√𝟐𝟐, 𝟐𝟓 𝐜𝐦²
(FME – Questão 619) Um cone tem 8 cm de altura e 15 cm de raio. Outro cone tem 15 cm de altura e 8 cm
de raio. Quanto a área lateral do primeiro excede a área lateral do segundo?
Solução
(i) Primeiro cone:
h = 8 cm
r = 15
(i) Cálculo da geratriz: g2
= h2
+ r2
→ g2
= 82
+ (15)2
→ g2
= 64 + 225 → g2
= 289 → 𝐠 = 𝟏𝟕 𝐜𝐦
(ii) Área lateral do primeiro cone: SL = πrg → SL = π. 15.17 → 𝐒𝐋 = 𝟐𝟓𝟓𝛑 𝐜𝐦²
(iii) Segundo cone:
h = 15 cm
r = 8 cm
(iv) Cálculo da geratriz:
g2
= h2
+ r2
→ g2
= (15)2
+ 82
→ g2
= 225 + 64 → g2
= 289 → g = 17
(v) Área lateral do segundo cone: SL = πrg → SL = π. 8.17 → 𝐒𝐋 = 𝟏𝟑𝟔𝛑 𝐜𝐦²

(vi) Temos, então: 255π cm2
− 136π cm2
= 𝟏𝟏𝟗 𝐜𝐦²
(FME – Questão 620) Determine a medida da altura de um cone, sendo 42 cm o diâmetro da base e 1050𝝅
cm² sua área total.
Solução
h = ?
Diâmetro = 42 cm
Raio r = 21 cm
(i) Área total do cone = 1050𝝅 cm²
ST = πr(g + r) → 1050π = π. 21(g + 21) → 441 + 21g = 1050 → 21g = 1050 − 441 → 21g = 609
g =
609
21
→ 𝐠 = 𝟐𝟗
(ii) Cálculo da altura:
g2
= h2
+ r2
→ (29)2
= h2
+ (21)2
→ 841 = h2
+ 441 → h2
= 400 → h = √400 → 𝐡 = 𝟐𝟎 𝐜𝐦
(FME – Questão 621) A altura de um cone circular reto cujo raio da base mede “r” é “𝝅𝒓". Sendo 3 cm a
medida do apótema do hexágono regular inscrito na base, determine a área da secção meridiana do cone.
Solução
Raio da base = r
Altura do cone = 𝝅𝒓
Apótema do hexágo inscrito = 3 cm
(iii) Área da secção meridiana do cone:
(i) No triângulo retângulo destacado ao lado, “ap” é o apótema do
hexágono. Logo:
𝑟2
= (𝑎𝑝)2
+ (
𝑟
2
)
2
→ 𝑟2
= 32
+
𝑟2
4
→ 𝑟2
= 9 +
𝑟2
4
→ 4𝑟2
= 36 + 𝑟2
→
4𝑟2
− 𝑟2
= 36 → 3𝑟2
= 36 ÷ 3 → 𝑟2
= 12 → 𝑟√4.3 → 𝐫 = 𝟐√𝟑 𝐜𝐦
(ii) A altura vale: h = πr → 𝐡 = 𝟐𝛑√𝟑 cm

(FME – Questão 622) O que ocorre com o volume de um cone de revolução se duplicarmos sua altura E se
duplicarmos o raio de sua base?
Solução
(i) Se sua altura vale “h”, se duplicarmos esta altura passa a ser: 2h, logo:
Vcone =
πr2
h
3
→ Vcone =
𝜋𝑟2
. 2ℎ
3
→ Vcone = 2. (
𝜋𝑟2
ℎ
3
)
Resposta: O volume do cone dobra.
(ii) Se duplicarmos o raio r, este passará a valer: 2r, logo:
Vcone =
πr2
h
3
→ Vcone =
𝜋(2𝑟)2
. ℎ
3
→ Vcone =
𝜋4𝑟2
. ℎ
3
→ Vcone = 4 (
𝜋𝑟2
ℎ
3
)
Resposta: O volume do cone quadruplica.
(FME – Questão 623) As dimensões de um paralelepípedo retângulo são: a, b, c. Qual é a altura de um cone
equivalente se o raio da base do cone mede “a”?
(i) Volume do paralelepípedo:
V =abc
(ii) Se o paralelepípedo e o cone são equivalentes, então, têm volumes iguais
Vcone = Vparalelepípedo →
πr2
h
3
= abc → πa2
h = 3abc → πah = 3bc → 𝐡 =
𝟑𝐛𝐜
𝛑𝐚
(FME – Questão 624) O volume de um cilindro reto é 𝟏𝟐𝟐𝟓𝝅 𝒄𝒎³ e sua altura é 35 cm. Determine o volume
de um cone de revolução, sendo sua base a mesma do cilindro e sua geratriz a geratriz do cilindro.
Solução
Vcilindro = πr2
h → 1225π = πr2
. 35 → r2
=
1225
35
→ 𝐫𝟐
= 𝟑𝟓
Pelo enunciado da questão: geratriz (g) do cilindro = altura (h) do cilindro, logo: g = h = 35 cm
Vcone =
πr2
h
3
→ Vcone =
35π. h
3
(i)
SSM =
b. h
2
→ SSM =
4√3. 2π√3
2
→ SSM = 4π. 3 → 𝐒𝐒𝐌 = 𝟏𝟐𝛑 𝐜𝐦²

Cálculo da altura do cone
g2
= r2
+ h2
→ (35)2
= 35 + h2
→ 1225 − 35 = h2
→ h2
= 1190 → 𝐡 = √𝟏𝟏𝟗𝟎(𝒊𝒊)
Substituindo (ii) em (i), temos:
𝑣 =
35𝜋. ℎ
3
→ 𝐯 =
𝟑𝟓𝛑√𝟏𝟏𝟗𝟎
𝟑
𝐜𝐦³
(FME – Questão 625) Determine o volume de um cone de revolução cuja secção meridiana é um triângulo
isósceles de área 4,8 dm², sendo 3 dm a altura do cone.
Solução
(ii) Volume do cone:
Vcone =
πr2
h
3
→ Vcone =
𝜋(1,6)2
. 3
3
→ 𝐕𝐜𝐨𝐧𝐞 = 𝟐, 𝟓𝟔𝛑 𝐝𝐦³
(FME – Questão 626) Determine a área lateral de um cone, sendo 3 cm a sua altura e 5 cm a soma da medida
da geratriz com o raio da base.
Solução
Área lateral = ?
h = 3 cm
g + r = 5 cm -----> g = 5 – r
g2
= r2
+ h2
→ (5 − r)2
= r2
+ 32
→ 25 − 10r + r2
= r2
+ 9 → −10r = 9 − 25 → −10r = −16(−10)
→ 𝒓 =
𝟏𝟔
𝟏𝟎
Logo:
g = 5 − r → g = 5 −
16
10
→ g =
50 − 16
10
→ 𝐠 =
𝟑𝟒
𝟏𝟎
Cálculo da área lateral:
SL = πrg → SL = π.
16
10
.
34
10
→ SL =
544π
100
÷
4
4
→ 𝐒𝐋 =
𝟏𝟑𝟔𝛑
𝟐𝟓
𝒄𝒎²
(FME – Questão 627) Determine a geratriz de um cone de revolução, sabendo que a área da base é
equivalente à secção meridiana do cone e que a altura desse cone mede 𝟗𝝅 cm.
(i) A área da secção meridiana vale = 4,8 dm², logo:
𝑆𝑆𝑀 =
𝑏. ℎ
2
→ 4,8 =
𝑏. 3
2
→ 3𝑏 = 9,6 → 𝑏 =
9,6
3
→ 𝐛 = 𝟑, 𝟐 𝐝𝐦
O raio da base do cone vale:
r =
3,2
2
→ 𝐫 = 𝟏, 𝟔 𝐝𝐦

Solução
Geratriz = ?
Área da base = Secção meridiana
Altura = 𝟗𝛑 cm
Obs: Na secção meridiana a base é igual a: b = 2r
Sb = SSM → πr2
=
b. h
2
→ πr2
=
2r. 9π
2
→ 𝐫 = 𝟗 𝐜𝐦
Cálculo da geratriz:
g2
= h2
+ r2
→ g2
= (9π)2
+ 92
→ g2
= 81π2
+ 81 → g2
= 81(π2
+ 1) → g = √81(π2 + 1) →
𝐠 = 𝟗√𝛑𝟐 + 𝟏 𝐜𝐦
(FME – Questão 628) O volume de um cone de revolução é 𝟏𝟐𝟖𝝅 cm³, sendo 8 cm o lado do hexágono inscrito
em sua base. Determine a relação entre a área total do cone e a área total de um cilindro que tenha o mesmo
volume e a mesma base do cone. Calcule ainda a medida do ângulo do setor circular obtido do
desenvolvimento da superfície lateral do cone.
Solução
r = raio da base comum
h1 = altura do cone
h2 = altura do cilindro
Dados:
r = 8
Vcone = Vcilindro = 128𝜋
(a) Relação entre a área do cone e a área total do cilindro:
(b) Cálculo da medida do ângulo do setor circular obtido do desenvolvimento da superfície lateral do cone:

θ =
2πr
g
→ θ =
360°. 8
10
→ 𝛉 = 𝟐𝟖𝟖°
(FME – Questão 629) Com um setor circular de 120° e raio R, construímos um cone. Calcule a área total e o
volume do cone.
Solução 1
Solução 2
Na base adotaremos o raio como: R/3, pois o setor de 120° é 3 vezes menor que a circunferência que tem
360°, logo:
Área da base
Sb = πR2
→ Sb = π (
R
3
)
2
→ 𝐒𝐛 =
𝛑𝐑²
𝟗
Área lateral
SL =
απR2
360°
→ SL =
120°πR2
360°
→ 𝐒𝐋 =
𝛑𝐑²
𝟑
Área total = Área da base + Área lateral:
ST =
πR2
9
+
πR2
3
→ ST =
πR2
+ 3πR2
9
→ 𝐒𝐋 =
𝟒𝛑𝐑𝟐
𝟗
O volume de um cone é:

V=
Para descobrir o h, fazemos Pitágoras no triangulo que está na imagem em anexo.
h=
Substituindo:
V=
V=
(FME – Questão 630) Determine o ângulo central de um setor obtido pelo desenvolvimento da superfície
lateral de um cone cujo raio da base mede 1 cm e cuja altura mede 3 cm.
Solução
Raio da base = 1 cm
Altura = 3 cm
A superfície lateral de um cone é um setor circular cujo comprimento do arco é 2.π.r, ou seja, é o
comprimento da circunferência da base.
Como o raio da base mede 1 cm, o arco mede
C= 2.π.1 ----> C= 2π
Pelo enunciado da questão, devemos ter:
(FME – Questão 631) Um cone circular reto tem 24 cm de altura e 7 cm de raio. Calcule em radianos a
medida do ângulo do setor circular que se obtém pelo desenvolvimento da superfície lateral do cone.
Solução
h = 24 cm
r = 7 cm
No triângulo retângulo destacado, temos:
g2
= h2
+ r2
→ g2
= 32
+ 12
→ g2
= 9 + 1 → g2
= 10 → 𝐠 = √𝟏𝟎
O ângulo do setor é dado por:
θ =
2πr
g
→ θ =
2π. 1
√10
→ θ =
2π
√10
.
√10
√10
→ θ =
2π√10
10
→ 𝛉 =
𝛑√𝟏𝟎
𝟓
𝐫𝐚𝐝 ou
θ =
180°√10
5
→ 𝛉 = (𝟑𝟔√𝟏𝟎)°

(FME – Questão 632) Um cone circular reto de altura h = 3 m tem área lateral igual a 6𝝅 m². Determine o
ângulo que a geratriz g faz com a reta suporte da altura h.
Solução
SL = 6π → πrg = 6π → rg = 6 → 𝐫 =
𝟔
𝐠
g2
= r2
+ h2
→ g2
= (
6
g
)
2
+ 32
→ g2
= (
36
g2
) + 9 → g2
−
36
g2
− 9 = 0 → g4
− 36 − 9g2
= 0 →
𝐠𝟒
− 𝟗𝐠𝟐
− 𝟑𝟔 = 𝟎
𝐅𝐚𝐳𝐞𝐧𝐝𝐨: 𝐠𝟒
= 𝐲𝟐
𝐞 𝐠𝟐
= 𝐲, 𝐭𝐞𝐦𝐨𝐬:
𝑦2
− 9𝑦 − 36 = 0 → ∆= 81 + 144 → ∆= 225
y =
9 ± √225
2
→ y =
9 ± 15
2
→ y′
= 12 ou y" = −3 (Não covém)
g2
= y → g2
= 12 → g = √12 → 𝐠 = 𝟐√𝟑 𝐦
Pelo triângulo retângulo formado pela geratriz (hipotenusa), raio e altura (catetos):
(FME – Questão 633) Um cilindro e um cone têm mesmo volume e igual altura “h”. Determine o raio do
cilindro em função do raio “r” da base do cone.
Solução
Sejam:
R = raio do cilindro
r = raio do cone
g2
= h2
+ r2
→ g2
= (24)2
+ 72
→ g2
= 576 + 49 → g2
= 625 →
g = √625 → 𝐠 = 𝟐𝟓
Cálculo do ângulo do setor:
θ =
2πr
g
→ θ =
2π. 7
25
→ 𝛉 =
𝟏𝟒𝛑
𝟐𝟓
𝐫𝐚𝐝
Cos θ =
3
2√3
→ Cos θ =
3
2√3
.
√3
√3
→ Cos θ =
3√3
2.3
→ 𝐂𝐨𝐬 𝛉 =
√𝟑
𝟐
Portanto:
𝛉 = 𝟑𝟎°

𝐕𝐜𝐢𝐥𝐢𝐧𝐝𝐫𝐨 = 𝐕𝐜𝐨𝐧𝐞 → πR2
h =
πr2h
3
→ R2
=
r2
3
→ R = √
r2
3
→ R =
r
√3
.
√3
√3
→ 𝐑 =
𝐫√𝟑
𝟑
(FME – Questão 634) Calcule a altura, a área lateral e o volume de um cone de revolução de raio R e base
equivalente à secção meridiana.
Solução
SL = πrg → SL = πR (R√π2 + 1) → 𝐒𝐋 = 𝛑𝐑𝟐
(√𝛑𝟐 + 𝟏)
(iv) Cálculo do volume:
Vcone =
πr2
h
3
→ Vcone =
πR2
. πR
3
→ 𝐕𝐜𝐨𝐧𝐞 =
𝛑²𝐑³
𝟑
(FME – Questão 635) Determine a razão entre a base e a superfície de um cone que tem altura igual ao
diâmetro da base.
Solução
Altura (h) = Diâmetro da base ----> h = 2r ou r = h/2
g2
= h2
+ r2
→ g2
= h2
+ (
h
2
)
2
→ g2
= h2
+
h2
4
→ g2
=
5h2
4
→ 𝐠 =
𝒉√𝟓
𝟐
Sb = πr² → Sb = π (
h
2
)
2
→ 𝐒𝐛 =
𝝅𝒉²
𝟒
Área total do cone:
ST = πr(g + r) → ST = π.
h
2
(
𝒉√𝟓
𝟐
+
ℎ
2
) → ST =
𝜋ℎ
2
(
ℎ√5 + ℎ
2
) →
ST =
𝜋ℎ
2
. [
ℎ(√5 + 1)
2
] →
𝜋ℎ2
√5 + 𝜋ℎ²
4
→ ST =
𝜋ℎ²(√5 + 1)
4
Razão entre a base e a superfície do cone:
𝐒𝐛
ST
=
𝝅𝒉¹
𝟒
𝜋ℎ²(√5 + 1)
4
→
𝝅𝒉²
𝟒
.
𝟒
𝜋ℎ²(√5 + 1)
→
𝟏
(√5 + 1)
.
(√5 − 1)
(√5 − 1)
→
√𝟓 − 𝟏
𝟓 − 𝟏
→
√𝟓 − 𝟏
𝟒
(i) Cálculo da altura:
Sb = SSM → πR2
=
2R. h
2
→ 𝛑𝐑 = 𝐡
(ii) Cálculo da geratriz:
g2
= h2
+ R2
→ g2
= π2
R2
+ R2
→ g2
= R2(π2
+ 1) →
g = √R²(π + 1) → 𝐠 = 𝐑√𝛑𝟐 + 𝟏

(FME – Questão 636) Sendo 7/5 a razão entre a área lateral e a área da base de um cone, determine a medida
do raio da base e da geratriz, sabendo que a altura do cone mede 𝟒√𝟔 cm.
Solução
h = 4√6
SLateral
Sbase
=
7
5
→
𝜋𝑟𝑔
𝜋𝑟2
=
7
5
→
𝑔
𝑟
=
7
5
→ 𝐠 =
𝟕𝐫
𝟓
g2
= h2
+ r2
→ g2
= (4√6)
2
+ r2
→ g2
− r2
= 96 → (
7r
5
)
2
− r2
= 96 →
49r2
25
− r2
= 96 →
24r2
25
= 96 →
r²
25
= 4 → r2
= 100 → 𝐫 = 𝟏𝟎 cm
g =
7r
5
→ g =
7.10
5
→ 𝐠 = 𝟏𝟒 𝐜𝐦
(FME – Questão 637) Um cilindro e um cone têm altura “h” e raio da base “r”. Sendo “r” o dobro de “h”,
determine a razão entre a área lateral do cilindro e a área lateral do cone.
Solução
r = 2h
g2
= h2
+ r2
→ g2
= h2
+ (2h)2
→ g2
= h2
+ 4h2
→ g2
= 5h2
→ 𝐠 = 𝐡√𝟓
SLateral do Cilindro
SLateral do Cone
=
2πrh
πrg
→
2π. 2h. h
π. 2h. 𝐡√𝟓
→
2
√5
.
√5
√5
→
𝟐√𝟓
𝟓
(FME – Questão 638) Determine o volume de um cone cujo raio da base mede “r”, sendo “3r” a soma das
medidas da geratriz com a altura do cone.
Solução
g + h = 3r ----> g = 3r – h (i)
g² = h² + r² (ii)
Substituindo (i) em (ii), temos:
(3r - h)² = h² + r² ----> 9r² - 6rh + h² = h² + r² ----> 8r² - 6rh = 0 : (r)----> 8r – 6h =0 ---->
6h = 8r ----> h = 8r/6
Volume do cone:
Vcone =
πr2
h
3
→ Vcone =
πr2
.
8r
6
3
→ Vcone =
8πr³
18
: (
2
2
) → 𝐕𝐜𝐨𝐧𝐞 =
𝟒𝛑𝐫³
𝟗
(FME – Questão 639) Calcule o raio da base de um cone de revolução, conhecendo a sua área total 𝝅𝒂² e sua
geratriz “g”.
(Resposta: )

(FME – Questão 640) Determine o volume de um cone de revolução cuja área lateral é igual a “A”, sabendo
que a geratriz do cone é igual a 4/5 do diâmetro da base do cone.
Solução
(FME – Questão 641) Determine o volume de um cone de revolução, sendo 126𝝅 cm² sua área lateral e 200 𝝅
cm² sua área total.
Solução
Área lateral = 126π cm2
Área total = 200π cm²
SL = πrg → πrg = 126π → rg = 126 → 𝐠 =
𝟏𝟐𝟔
𝐫
(𝐢)
ST = πr(g + r) → πr(g + r) = 200π → 𝐫𝐠 + 𝐫𝟐
= 𝟐𝟎𝟎 (𝐢𝐢)
Substituindo (i) em (ii), resulta em:
rg + r2
= 200 → r (
126
r
) + r2
= 200 → 126 + r2
= 200 → r2
= 200 − 126 → r² = 74 → r = √74 (iii)
Sendo:
g2
= h2
+ r2
→ (
126
r
)
2
= h2
+ 74 →
15876
r2
= h2
+ 74 →
15876
74
= h2
+ 74 → 74h2
+ 5476 = 15876
→ 74h2
= 15876 − 5476 → 74h2
= 10400 → h2
=
10400
74
→ h = √
10400
74
→ h = √
22. 22. 2.52. 13
74
→
h =
20√26
√74
→ h =
20√26
√74
.
√74
√74
→ h =
20√1924
74
→ h =
10√22. 481
37
→ h =
10.2√481
37
→ 𝐡 =
𝟐𝟎√𝟒𝟖𝟏
𝟑𝟕
Área da base:
Sb = πr² → 𝐒𝐛 = 𝟕𝟒𝛑

Volume do cone
Vcone =
𝐒𝐛. h
3
→ Vcone =
𝟕𝟒𝛑.
𝟐𝟎√𝟒𝟖𝟏
𝟑𝟕
3
→ Vcone =
2π. 20√481
3
→ 𝐕𝐜𝐨𝐧𝐞 =
𝟒𝟎𝛑√𝟒𝟖𝟏
𝟑
𝐜𝐦³
(FME – Questão 642) Calcule o volume de um cone equilátero em função de sua área total “S”.
Solução
(i) A secção meridiana de um cone equilátero é um triângulo equilátero, logo, sua altura é igual a altura do
cone:
(2r)² = h² + r² ----> 4r² = h² + r² ----> h² = 4r²- r² ---> h² = 3r² ----> h = √3r² → 𝐡 = 𝐫√𝟑
No cone equilátero: g = 2r
(ii) Área total = Área da base + Área lateral:
ST = Sb + SL → S = πr2
+ 2πr2
→ S = 3πr2
→ r2
=
S
3π
→ r = √
S
3π
→ r =
√S
√3π
.
√3π
√3π
→
r =
√S. 3π
3π
(iii) O volume do cone equilátero é dado por:
V =
πr2
h
3
→ V =
πr2
. r√3
3
→ 𝐕 =
√𝟑
𝟑
𝛑𝐫𝟑
V =
√3
3
π. (
√S. 3π
3π
)
3
→ V =
√3
3
π. (
√S. 3π
3π
)
2
. (
√S. 3π
3π
) → V =
√3
3
π.
S. 3π
9π2
.
√S. 3π
3π
→
V =
√3
3
.
S. 3π²
9π²
.
√S. 3π
3π
→ V =
S√S. 3π. 3
27π
→ V =
S√S. 9π
27π
→ V =
3S√Sπ
27π
→ 𝐕 =
𝐒√𝐒𝛑
𝟗𝛑
(FME – Questão 643) O raio da base, a altura, e a geratriz de um cone reto formam, nessa ordem, uma
Progressão Aritmética (PA). Determine esses elementos, sabendo que o volume do cone é 𝟏𝟒𝟒𝝅 cm³.
Solução
PA (raio, altura, geratriz)
Seja “R” a razão da PA.

Sejam:
Raio r = h – R
Altura = h
Geratriz = h + R
Temos:
g2
= h2
+ r²
(h + R)2
= h2
+ (h − R)2
→
h2
+ 2hR + R2
= h2
+ h2
− 2hR + R2
→
2hR + 2hR = h2
→
h(2R + 2R) = h2
÷ (h) →
4R = h →
R =
h
4
(i)
Vcone = 144π →
πr2
h
3
= 144𝜋 →
(h − R)2
. h
3
= 144 →
(𝐡 − 𝐑)𝟐
. 𝐡 = 𝟒𝟑𝟐 (𝐢𝐢) → Substitindo (i) em (ii), resulta em:
(h − R)2
. h = 432 →
(h −
h
4
)
2
. h = 432 →
(
3h
4
)
2
. h = 432 →
9h2
16
. h = 432 →
h3
16
= 48 →
h3
= 768 →
h = √768
3
→
h = √23. 23. 4.3
3
→
𝐡 = 𝟒√𝟏𝟐
𝟑
(𝐢𝐢𝐢)
Substituindo (iii) em (i), temos:
R =
h
4
→
𝑅 =
4√12
3
4
→
𝐑 = √𝟏𝟐
𝟑
Sendo:
r = h − R → r = 4√12
3
− √12
3
→ 𝐫 = 𝟑√𝟏𝟐
𝟑

g = h + r → g = 4√12
3
+ √12
3
→ 𝐠 = 𝟓√𝟏𝟐
𝟑
Resposta:
Raio = 𝟑√𝟏𝟐
𝟑
; altura = 𝟒√𝟏𝟐
𝟑
; geratriz = 𝟓√𝟏𝟐
𝟑
(FME – Questão 644) Desenvolvendo a superfície lateral de um cone reto, obtém-se um setor circular de raio
10 cm e ângulo central 135°. Calcule o volume desse cone.
(FME – Questão 645) Um semicone reto tem altura igual ao raio e o volume é 576𝝅 cm³. Calcule a área lateral
do semicone.
Solução
(FME – Questão 646) A geratriz de um cone de revolução mede 25 cm e a diagonal menor do hexágono regular
inscrito na base do cone mede 𝟕√𝟑 cm. Determine a área total e o volume do cone.
Solução
(FME – Questão 647) Determine o volume de um cone de revolução cuja área lateral é 60𝝅 cm², sendo 4,8
cm a distância do centro da base à geratriz do cone.
Solução

(FME – Questão 648) O diâmetro da base de um cone mede os 3/5 da sua altura e a área lateral é 100𝝅 dm³.
Calcule a medida da geratriz do cone.
Solução
(FME – Questão 649) Demonstre que o volume de um cone é igual ao produto da sua área lateral pela terça
parte da distância do centro de sua base à geratriz do cone.
Solução

Sejam r = raio da baase, h = altura, g =geratriz, x = distância do centro O da base à geratriz, V o vértice, AOB
um diâmetro da base
No triângulo retângulo VOB ---> r.h = x.g ---> x = h.r/g
S = pi.r.g
V = S.(x/3) ---> V = pi.r.g.(h.r/g)/3 ---> V = pi.r².h/3
(FME – Questão 650) Um sólido é formado pela superposição de cone sobre um cilindro de raio da base “r”.
Sendo a altura do sólido o triplo do raio “r” e a área lateral do sólido o quíntuplo da área da base do
cilindro, calcule o volume do sólido em função de “r”.
Solução
(FME – Questão 651) Um semicone tem área lateral igual a (√𝟐 𝝅 + 𝟐) cm². Determine a medida da sua
geratriz, sabendo que o raio da base tem medida igual à altura do semicone.
(FME – Questão 652) Determine a medida do raio da base e da geratriz de um cone, sendo “h” a medida de
sua altura e 𝝅 m² a sua área total.
Solução
(FME – Questão 653) Calcule o volume de um cone de revolução, conhecendo a área lateral “A” e o
apótema “g”.
(FME – Questão 654) Calcule o volume de um cone de revolução, conhecendo a área total “S” e a altura “h”.
Solução

(FME – Questão 655) Calcule o volume “V” de um cone de revolução em função de sua área lateral “A” e de
sua área total “S”.
Solução
------------------------------------------------------------------

Cone questões resolvidas - fundamentos de matemática elementar

More Related Content

What's hot

Similar to Cone questões resolvidas - fundamentos de matemática elementar

Recently uploaded

Cone questões resolvidas - fundamentos de matemática elementar