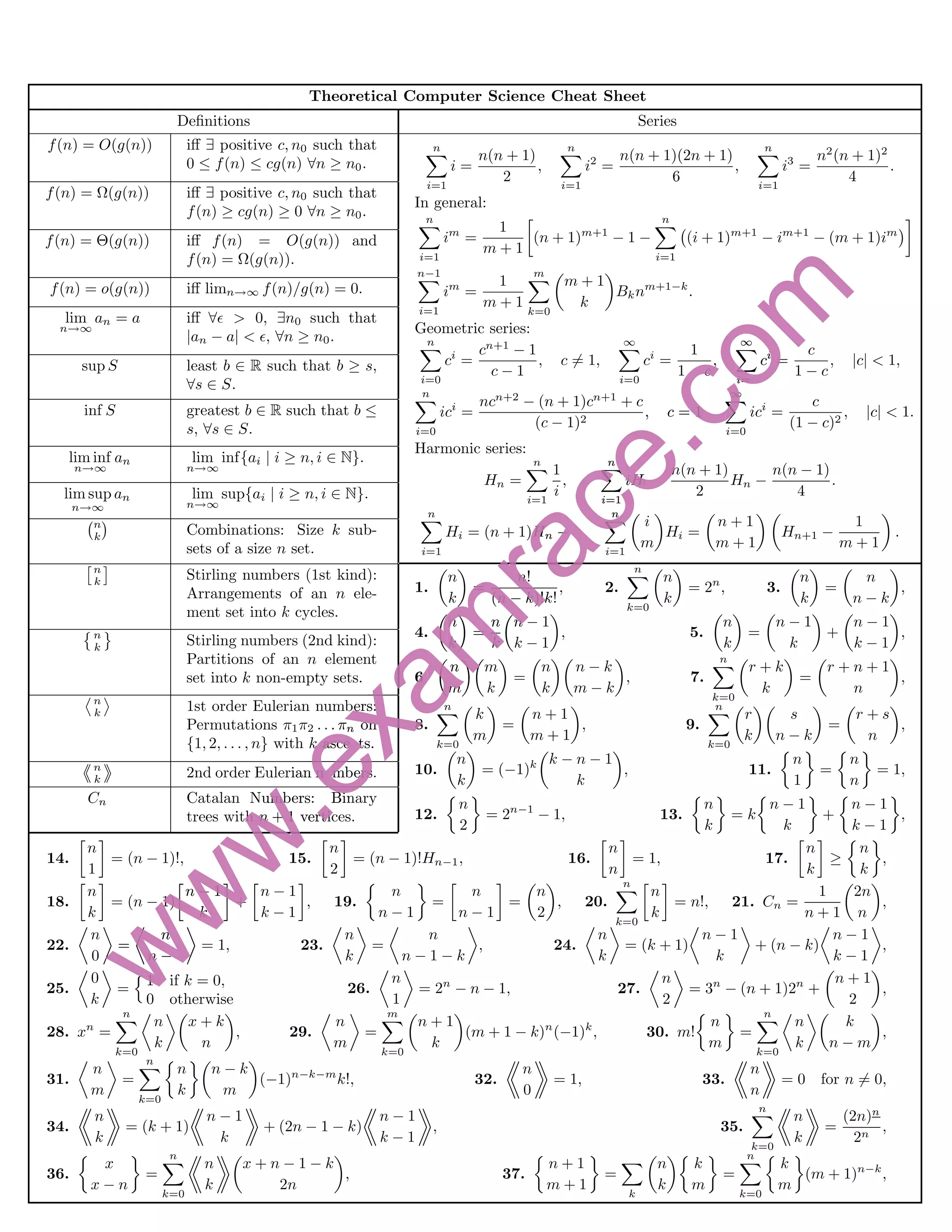
1. The document provides definitions and identities relating to theoretical computer science topics like asymptotic analysis, series, recurrences, and discrete structures.
2. It includes definitions for big O, Omega, and Theta notation used to describe the asymptotic behavior of functions.
3. Recurrences, like the master method, are presented for analyzing the runtime of divide-and-conquer algorithms.
4. Discrete structures like combinations, Stirling numbers, and trees are also covered, along with their properties and relationships.

![Theoretical Computer Science Cheat Sheet
π ≈ 3.14159, e ≈ 2.71828, γ ≈ 0.57721, φ = 1+
√
5
2 ≈ 1.61803, ˆφ = 1−
√
5
2 ≈ −.61803
i 2i
pi General Probability
1 2 2 Bernoulli Numbers (Bi = 0, odd i = 1):
B0 = 1, B1 = −1
2 , B2 = 1
6 , B4 = − 1
30 ,
B6 = 1
42 , B8 = − 1
30 , B10 = 5
66 .
Change of base, quadratic formula:
logb x =
loga x
loga b
,
−b ±
√
b2 − 4ac
2a
.
Euler’s number e:
e = 1 + 1
2 + 1
6 + 1
24 + 1
120 + · · ·
lim
n→∞
1 +
x
n
n
= ex
.
1 + 1
n
n
< e < 1 + 1
n
n+1
.
1 + 1
n
n
= e −
e
2n
+
11e
24n2
− O
1
n3
.
Harmonic numbers:
1, 3
2 , 11
6 , 25
12 , 137
60 , 49
20 , 363
140 , 761
280 , 7129
2520 , . . .
ln n < Hn < ln n + 1,
Hn = ln n + γ + O
1
n
.
Factorial, Stirling’s approximation
1, 2, 6, 24, 120, 720, 5040, 40 20, 362880, . . .
n! =
√
2πn
n
e
n
1 + Θ
1
n
.
Ackermann s fun tion and inverse:
a( , j) =
2j
i = 1
a(i − 1, 2) j = 1
a(i − 1, a(i, j − 1)) i, j ≥ 2
α(i) = min{j | a(j, j) ≥ i}.
Continuous distributions: If
Pr[a < X < b] =
b
a
p(x) dx,
then p is the probability density function of
X. If
Pr[X < a] = P(a),
then P is the distribu ion fun tion of X. If
P and p both exist then
P(a) =
a
−
p(x) dx.
Expectation: If X is discrete
E[g(X)]
x
g(x) Pr[X = x].
I X continuous then
E[g(X)] =
∞
−∞
g(x)p(x) dx =
∞
−∞
g(x) dP(x).
Variance, standard deviation:
VAR[X] = E[X2
] − E[X]2
,
σ = VAR[X].
For events A and B:
Pr[A ∨ B] = Pr[A] + Pr[B] − Pr[A ∧ B]
Pr[A ∧ B] = Pr[A] · Pr[B],
iff A and B are independent.
Pr[A|B] =
Pr[A ∧ B]
Pr[B]
For random variables X and Y :
E[X · Y ] = E[X] · E[Y ],
if X and Y are independent.
E[X + Y ] = E[X] + E[Y ],
E[cX] = c E[X].
Bayes’ theorem:
Pr[Ai|B] =
Pr[B|Ai] Pr[Ai]
n
j=1 Pr[Aj] Pr[B|Aj]
.
Inclusion-exclusion:
Pr
n
i=1
Xi =
n
i=1
Pr[Xi] +
n
k=2
(−1)k+1
ii<···<ik
Pr
k
j=1
Xij
.
Moment inequalities:
Pr |X| ≥ λ E[X] ≤
1
λ
,
Pr X − E[X] ≥ λ · σ ≤
1
λ2
.
Geometric distribution:
Pr[X = k] = pqk−1
, q = 1 − p,
E[X] =
∞
k=1
kpqk−1
=
1
p
.
2 4 3
3 8 5
4 16 7
5 32 11
6 64 13
7 128 17
8 256 19
9 512 23
10 1,024 29
11 2,048 31
12 4,096 37
13 8,192 41
14 16,384 43
15 32,768 47
16 65,536 53
17 131,072 59
18 262,144 61
19 524,288 67
20 1,048,576 71
21 2,097,152 73
22 4,194,304 79
23 8,388,608 83
24 16,777,216 89
25 33,554,432 97
26 67,108,864 101
27 134,217,728 103
28 268,435,456 107 Binomial distribution:
Pr[X = k] =
n
k
pk
qn−k
, q = 1 − p,
E[X] =
n
k=1
k
n
k
pk
qn−k
= np.
Poisson distribution:
Pr[X = k] =
e−λ
λk
k!
, E[X] = λ.
Normal (Gaussian) distribution:
p(x) =
1
√
2πσ
e−(x−µ)2
/2σ2
, E[X] = µ.
The “coupon collector”: We are given a
random coupon each day, and there are n
different types of coupons. The distribu-
tion of coupons is uniform. The expected
number of days to pass before we to col-
lect all n types is
nHn.
29 536,870,912 109
30 1,073,741,824 113
31 2,147,483,648 27
32 4,294,967 296 131
Pasca ’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
w
w
w
.exam
race.com
is the probability density function of
w
w
w
.exam
race.com
is the probability density function of
] =
w
w
w
.exam
race.com
] = P
w
w
w
.exam
race.com
P(
w
w
w
.exam
race.com
(a
w
w
w
.exam
race.com
a)
w
w
w
.exam
race.com
),
w
w
w
.exam
race.com
,
is the distribu ion fun tion of
w
w
w
.exam
race.com
is the distribu ion fun tion of
both exist then
w
w
w
.exam
race.com
both exist then
P
w
w
w
.exam
race.com
P(
w
w
w
.exam
race.com
(a
w
w
w
.exam
race.com
a) =
w
w
w
.exam
race.com
) =
w
w
w
.exam
race.com
a
w
w
w
.exam
race.com
a
−
w
w
w
.exam
race.com
−−
w
w
w
.exam
race.com
−
p
w
w
w
.exam
race.com
p(
w
w
w
.exam
race.com
(
Expectation: If
w
w
w
.exam
race.com
Expectation: If X
w
w
w
.exam
race.com
X
w
w
w
.exam
race.com
, . . .
w
w
w
.exam
race.com
, . . .
w
w
w
.exam
race.com
1
w
w
w
.exam
race.com
1
w
w
w
.exam
race.com
n
w
w
w
.exam
race.com
n
w
w
w
.exam
race.com
.
w
w
w
.exam
race.com
.
Factorial, Stirling’s approximation
w
w
w
.exam
race.com
Factorial, Stirling’s approximation
1, 2, 6, 24, 120, 720, 5040, 40 20, 362880,
w
w
w
.exam
race.com
1, 2, 6, 24, 120, 720, 5040, 40 20, 362880,
w
w
w
.exam
race.com
2
w
w
w
.exam
race.com
2πn
w
w
w
.exam
race.com
πn
w
w
w
.exam
race.com
n
w
w
w
.exam
race.com
n
w
w
w
.exam
race.com
e
w
w
w
.exam
race.com
e
w
w
w
.exam
race.com
n
w
w
w
.exam
race.com
n
w
w
w
.exam
race.com
1 + Θ
w
w
w
.exam
race.com
1 + Θ
Ackermann s fun tion and inverse:
w
w
w
.exam
race.com
Ackermann s fun tion and inverse:
a
w
w
w
.exam
race.coma(
w
w
w
.exam
race.com( , j
w
w
w
.exam
race.com, j) =
w
w
w
.exam
race.com) =
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
2
w
w
w
.exam
race.com
2j
w
w
w
.exam
race.com
j
a
w
w
w
.exam
race.coma(
w
w
w
.exam
race.com(i
w
w
w
.exam
race.comi
a
w
w
w
.exam
race.coma
α
w
w
w
.exam
race.comα(
w
w
w
.exam
race.com(i
w
w
w
.exam
race.comi) = min
w
w
w
.exam
race.com) = min
w
w
w
.exam
race.com
is discrete
w
w
w
.exam
race.com
is discrete
E
w
w
w
.exam
race.com
E[
w
w
w
.exam
race.com
[g
w
w
w
.exam
race.com
g(
w
w
w
.exam
race.com
(X
w
w
w
.exam
race.com
X)]
w
w
w
.exam
race.com
)]
w
w
w
.exam
race.com
I
w
w
w
.exam
race.com
I X
w
w
w
.exam
race.com
X continuous then
w
w
w
.exam
race.com
continuous then
E
w
w
w
.exam
race.com
E[
w
w
w
.exam
race.com
[g
w
w
w
.exam
race.com
g(
w
w
w
.exam
race.com
(X
w
w
w
.exam
race.com
X)] =
w
w
w
.exam
race.com
)] =
Variance, standard deviation:
w
w
w
.exam
race.com
Variance, standard deviation:
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com107
w
w
w
.exam
race.com107
w
w
w
.exam
race.comBinomial distribution:
w
w
w
.exam
race.comBinomial distribution:
Pr[
w
w
w
.exam
race.comPr[109
w
w
w
.exam
race.com109
w
w
w
.exam
race.com
w
w
w
.exam
race.com
113
w
w
w
.exam
race.com
113
w
w
w
.exam
race.com
2,147,483,648
w
w
w
.exam
race.com
2,147,483,648
w
w
w
.exam
race.com
27
w
w
w
.exam
race.com
27
4,294,967 296
w
w
w
.exam
race.com
4,294,967 296
w
w
w
.exam
race.com
131
w
w
w
.exam
race.com
131
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
Pasca ’s Triangle
w
w
w
.exam
race.com
Pasca ’s Triangle
w
w
w
.exam
race.com
1
w
w
w
.exam
race.com
1
1 1
w
w
w
.exam
race.com
1 1
1 2 1
w
w
w
.exam
race.com
1 2 1](https://image.slidesharecdn.com/computer-science-formulas-150117013521-conversion-gate01/75/Computer-science-formulas-3-2048.jpg)

![Theoretical Computer Science Cheat Sheet
Number Theory Graph Theory
The Chinese remainder theorem: There ex-
ists a number C such that:
C ≡ r1 mod m1
...
...
...
C ≡ rn mod mn
if mi and mj are relatively prime for i = j.
Euler’s function: φ(x) is the number of
positive integers less than x relatively
prime to x. If
n
i=1 pei
i is the prime fac-
torization of x then
φ(x) =
n
i=1
pei−1
i (pi − 1).
Euler’s theorem: If a and b are relatively
prime then
1 ≡ aφ(b)
mod b.
Fermat’s theorem:
1 ≡ ap−1
mod p.
The Euclidean algorithm: if a > b are in-
tegers then
gcd(a, b) = gcd(a mod b, b).
If
n
i=1 pei
i is the prime factorization of x
then
S(x) =
d|x
d =
n
i=1
pei+1
i − 1
pi − 1
.
Perfect Numbers: x is an even perfect num-
ber iff x = 2n−1
(2n
−1) and 2n
−1 is prime.
Wilson’s theorem: n is a prime iff
(n − 1)! ≡ −1 mod n.
M¨obius inversion:
µ(i) =
1 if i = 1.
0 if i is not squ re-free.
(−1)r
if i is th product f
r distin t prim s.
If
G(a) =
d|a
F(d),
then
F(a) =
d|a
µ(d)G
a
d
.
Prime numbers:
pn = n ln n + n ln ln n − n + n
ln ln n
ln n
+ O
n
ln n
,
π(n) =
n
ln n
+
n
(ln n)2
+
2!n
(ln n)3
+ O
n
(ln n)4
.
Definitions:
Loop An edge connecting a ver-
tex to itself.
Directed Each edge has a direction.
Simple Graph with no loops or
multi-edges.
Walk A sequence v0e1v1 . . . e v .
Trail A walk with distinct edges.
Path A trail with distinct
vertices.
Connected A graph where there exists
a path between any two
vertices.
Component A maximal connected
subgraph.
Tree A connected acyclic graph.
Free tree A tree with no root.
DAG Directed acyclic graph.
Eulerian Graph with a tra l visiting
each edge exactly once.
Hamiltonian Graph with a cy le visiting
each vertex exact y once.
Cut A set of edg s whose re-
m l in reases the num-
ber of omponents.
Cut-set A minimal cut.
Cut edge A size 1 cut.
k-Connec ed A graph connected with
the removal of any k − 1
vertices.
k T ugh ∀S ⊆ V, S = ∅ we have
k · c(G − S) ≤ |S|.
k-Regular A graph where all vertices
have degree k.
k-Factor A k-regular spanning
subgraph.
Matching A set of edges, no two of
which are adjacent.
Clique A set of vertices, all of
which are adjacent.
Ind. set A set of vertices, none of
which are adjacent.
Vertex cover A set of vertices which
cover all edges.
Planar graph A graph which can be em-
beded in the plane.
Plane graph An embedding of a planar
graph.
v∈V
deg(v) = 2m.
If G is planar then n − m + f = 2, so
f ≤ 2n − 4, m ≤ 3n − 6.
Any planar graph has a vertex with de-
gree ≤ 5.
Notation:
E(G) Edge set
V (G) Vertex set
c(G) Number of components
G[S] Induced subgraph
deg(v) Degree of v
∆(G) Maximum degree
δ(G) Minimum degr e
χ(G) Chromatic number
χE(G) Edge hroma ic number
Gc
Complement graph
Kn Comp ete graph
K 1,n2
Complete bipartite graph
r k, ) Ramsey number
Geometry
Pr jective coordinates: triples
(x, y, z), not all x, y and z zero.
(x, y, z) = (cx, cy, cz) ∀c = 0.
Cartesian Projective
(x, y) (x, y, 1)
y = mx + b (m, −1, b)
x = c (1, 0, −c)
Distance formula, Lp and L∞
metric:
(x1 − x0)2 + (y1 − y0)2,
|x1 − x0|p
+ |y1 − y0|p 1/p
,
lim
p→∞
|x1 − x0|p
+ |y1 − y0|p 1/p
.
Area of triangle (x0, y0), (x1, y1)
and (x2, y2):
1
2 abs
x1 − x0 y1 − y0
x2 − x0 y2 − y0
.
Angle formed by three points:
θ
(0, 0) (x1, y1)
(x2, y2)
2
1
cos θ =
(x1, y1) · (x2, y2)
1 2
.
Line through two points (x0, y0)
and (x1, y1):
x y 1
x0 y0 1
x1 y1 1
= 0.
Area of circle, volume of sphere:
A = πr2
, V = 4
3 πr3
.
If I have seen farther than others,
it is because I have stood on the
shoulders of giants.
– Issac Newton
w
w
w
.exam
race.com
A connected acyclic graph.
w
w
w
.exam
race.com
A connected acyclic graph.
Directed acyclic graph.
w
w
w
.exam
race.com
Directed acyclic graph.
Graph with a tra l visiting
w
w
w
.exam
race.com
Graph with a tra l visiting
each edge exactly once.
w
w
w
.exam
race.com
each edge exactly once.
Graph with a cy le visiting
w
w
w
.exam
race.com
Graph with a cy le visiting
each vertex exact y once.
w
w
w
.exam
race.com
each vertex exact y once.
A set of edg s whose re-
w
w
w
.exam
race.com
A set of edg s whose re-
m l in reases the num-
w
w
w
.exam
race.com
m l in reases the num-
ber of omponents.
w
w
w
.exam
race.com
ber of omponents.
A minimal cut.
w
w
w
.exam
race.com
A minimal cut.
Cut edge
w
w
w
.exam
race.com
Cut edge A size 1 cut.
w
w
w
.exam
race.com
A size 1 cut.
k-Connec ed
w
w
w
.exam
race.com
k-Connec ed A graph connected with
w
w
w
.exam
race.com
A graph connected with
the removal of any
w
w
w
.exam
race.com
the removal of any
k T ugh
w
w
w
.exam
race.com
k T ugh
k-Regular
w
w
w
.exam
race.comk-Regular
w
w
w
.exam
race.com
) Maximum degree
w
w
w
.exam
race.com
) Maximum degree
) Minimum degr e
w
w
w
.exam
race.com
) Minimum degr e
) Chromatic number
w
w
w
.exam
race.com
) Chromatic number
) Edge hroma ic number
w
w
w
.exam
race.com
) Edge hroma ic number
Complement graph
w
w
w
.exam
race.com
Complement graph
Comp ete graph
w
w
w
.exam
race.com
Comp ete graph
K
w
w
w
.exam
race.com
K
w
w
w
.exam
race.com
KK
w
w
w
.exam
race.com
KK 1
w
w
w
.exam
race.com
1,n
w
w
w
.exam
race.com
,n2
w
w
w
.exam
race.com
2
Complete bipartite graph
w
w
w
.exam
race.com
Complete bipartite graph
r
w
w
w
.exam
race.com
r
w
w
w
.exam
race.com
k,
w
w
w
.exam
race.com
k, ) Ramsey number
w
w
w
.exam
race.com
) Ramsey number
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
1 is prime.
w
w
w
.exam
race.com
1 is prime.
is not squ re-free.
w
w
w
.exam
race.comis not squ re-free.
is th product f
w
w
w
.exam
race.comis th product f
distin t prim s.
w
w
w
.exam
race.com
distin t prim s.
a
w
w
w
.exam
race.com
a) =
w
w
w
.exam
race.com
) =
w
w
w
.exam
race.com
d
w
w
w
.exam
race.com
d|
w
w
w
.exam
race.com
|a
w
w
w
.exam
race.com
a
F
w
w
w
.exam
race.com
F(
w
w
w
.exam
race.com
(d
w
w
w
.exam
race.com
d)
w
w
w
.exam
race.com
)
F
w
w
w
.exam
race.com
F(
w
w
w
.exam
race.com
(a
w
w
w
.exam
race.com
a) =
w
w
w
.exam
race.com
) =
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
Pr jective coordinates: triples
w
w
w
.exam
race.com
Pr jective coordinates: triples
(
w
w
w
.exam
race.com
(x, y, z
w
w
w
.exam
race.com
x, y, z](https://image.slidesharecdn.com/computer-science-formulas-150117013521-conversion-gate01/75/Computer-science-formulas-5-2048.jpg)



![Theoretical Computer Science Cheat Sheet
Series Escher’s Knot
Expansions:
1
(1 − x)n+1
ln
1
1 − x
=
∞
i=0
(Hn+i − Hn)
n + i
i
xi
,
1
x
−n
=
∞
i=0
i
n
xi
,
xn
=
∞
i=0
n
i
xi
, (ex
− 1)n
=
∞
i=0
i
n
n!xi
i!
,
ln
1
1 − x
n
=
∞
i=0
i
n
n!xi
i!
, x cot x =
∞
i=0
(−4)i
B2ix2i
(2i)!
,
tan x =
∞
i=1
(−1)i−1 22i
(22i
− 1)B2ix2i−1
(2i)!
, ζ(x) =
∞
i=1
1
ix
,
1
ζ(x)
=
∞
i=1
µ(i)
ix
,
ζ(x − 1)
ζ(x)
=
∞
i=1
φ(i)
ix
,
Stieltjes Integrat onζ(x) =
p
1
1 − p−x
,
ζ2
(x) =
∞
i=1
d(i)
xi
where d(n) = d|n 1,
ζ(x)ζ(x − 1) =
∞
i=1
S(i)
xi
where S(n) = d|n d,
ζ(2n) =
22n−1
|B2n|
(2n)!
π2n
, n ∈ N,
x
sin x
=
∞
i=0
(−1)i−1 (4i
− 2)B2ix2i
(2i)!
,
1 −
√
1 − 4x
2x
n
=
∞
i=0
n(2i + n − 1)!
i!(n + i)!
xi
,
ex
sin x =
∞
i=1
2i/2
sin iπ
4
i!
xi
,
1 −
√
1 − x
x
=
∞
i=0
(4i)!
16i
√
2(2i)!(2i + 1)!
x ,
arcsin x
x
2
=
∞
i=0
4i
i 2
(i + 1)(2i + 1)!
x2i
.
If G is continuous in the interval [a b] and F is nondecreasing then
b
G(x) dF(x)
exists. If a ≤ b ≤ c then
c
a
G(x) dF(x) =
b
a
G(x) dF(x) +
c
b
G(x) dF(x).
If the i egral involved exist
b
a
G(x) + H(x) dF(x) =
b
a
G(x) dF(x) +
b
a
H(x) dF(x),
b
a
G(x) d F(x) + H(x) =
b
a
G(x) dF(x) +
b
a
G(x) dH(x),
b
a
c · G(x) dF(x) =
b
a
G(x) d c · F(x) = c
b
a
G(x) dF(x),
b
a
G(x) dF(x) = G(b)F(b) − G(a)F(a) −
b
a
F(x) dG(x).
If the integrals involved exist, and F possesses a derivative F at every
point in [a, b] then
b
a
G(x) dF(x) =
b
a
G(x)F (x) dx.
Cram r’s R
00 47 18 76 29 93 85 34 61 52
86 11 57 28 70 39 94 45 02 63
95 80 22 67 38 71 49 56 13 04
59 96 81 33 07 48 72 60 24 15
73 69 90 82 44 17 58 01 35 26
68 74 09 91 83 55 27 12 46 30
37 08 75 19 92 84 66 23 50 41
14 25 36 40 51 62 03 77 88 99
21 32 43 54 65 06 10 89 97 78
42 53 64 05 16 20 31 98 79 87
Fibonacci Numbers
If we have equations:
a1,1x1 + a 2x2 + · · · + a1,nxn = b1
a2,1x1 + a2,2x2 + · · · + a2,nxn = b2
...
...
...
an,1x1 + an,2x2 + · · · + an,nxn = bn
Let A = (ai,j) and B be the column matrix (bi). Then
there is a unique solution iff det A = 0. Let Ai be A
with column i replaced by B. Then
xi =
det Ai
det A
.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . . .
Definitions:
Fi = Fi−1+Fi−2, F0 = F1 = 1,
F−i = (−1)i−1
Fi,
Fi = 1√
5
φi
− ˆφi
,
Cassini’s identity: for i > 0:
Fi+1Fi−1 − F2
i = (−1)i
.
Additive rule:
Fn+k = FkFn+1 + Fk−1Fn,
F2n = FnFn+1 + Fn−1Fn.
Calculation by matrices:
Fn−2 Fn−1
Fn−1 Fn
=
0 1
1 1
n
.
The Fibonacci number system:
Every integer n has a unique
representation
n = Fk1
+ Fk2
+ · · · + Fkm
,
where ki ≥ ki+1 + 2 for all i,
1 ≤ i < m and km ≥ 2.
Improvement makes strait roads, but the crooked
roads without Improvement, are roads of Genius.
– William Blake (The Marriage of Heaven and Hell)
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.com
Stieltjes Integrat on
w
w
w
.exam
race.com
Stieltjes Integrat on
w
w
w
.exam
race.com
w
w
w
.exam
race.com
w
w
w
.exam
race.comi
w
w
w
.exam
race.comi)!
w
w
w
.exam
race.com)!
w
w
w
.exam
race.com2(2
w
w
w
.exam
race.com2(2i
w
w
w
.exam
race.comi)!(2
w
w
w
.exam
race.com)!(2i
w
w
w
.exam
race.comi + 1)!
w
w
w
.exam
race.com+ 1)!
x
w
w
w
.exam
race.comx
w
w
w
.exam
race.com=0
w
w
w
.exam
race.com=0
4
w
w
w
.exam
race.com4i
w
w
w
.exam
race.comi
i
w
w
w
.exam
race.comi
w
w
w
.exam
race.com2
w
w
w
.exam
race.com2
w
w
w
.exam
race.com(
w
w
w
.exam
race.com(i
w
w
w
.exam
race.comi + 1)(2
w
w
w
.exam
race.com+ 1)(2i
w
w
w
.exam
race.comi + 1)!
w
w
w
.exam
race.com+ 1)!
w
w
w
.exam
race.com
is continuous in the interval [
w
w
w
.exam
race.com
is continuous in the interval [a b
w
w
w
.exam
race.com
a b] and
w
w
w
.exam
race.com
] and
w
w
w
.exam
race.com
b
w
w
w
.exam
race.com
b
w
w
w
.exam
race.com
w
w
w
.exam
race.com
G
w
w
w
.exam
race.com
G(
w
w
w
.exam
race.com
(
b
w
w
w
.exam
race.com
b ≤
w
w
w
.exam
race.com
≤ c
w
w
w
.exam
race.com
c then
w
w
w
.exam
race.com
then
w
w
w
.exam
race.com
a
w
w
w
.exam
race.com
aa
w
w
w
.exam
race.com
a
G
w
w
w
.exam
race.com
G(
w
w
w
.exam
race.com
(x
w
w
w
.exam
race.com
x)
w
w
w
.exam
race.com
) dF
w
w
w
.exam
race.com
dF(
w
w
w
.exam
race.com
(x
w
w
w
.exam
race.com
x) =
w
w
w
.exam
race.com
) =
If the i egral involved exist
w
w
w
.exam
race.com
If the i egral involved exist
w
w
w
.exam
race.com
b
w
w
w
.exam
race.com
b
a
w
w
w
.exam
race.com
aa
w
w
w
.exam
race.com
a
w
w
w
.exam
race.com
G
w
w
w
.exam
race.com
G(
w
w
w
.exam
race.com
(
w
w
w
.exam
race.com
x
w
w
w
.exam
race.com
x) +
w
w
w
.exam
race.com
) +
w
w
w
.exam
race.com
b
w
w
w
.exam
race.com
b
G
w
w
w
.exam
race.com
G
w
w
w
.exam
race.com
Cram r’s R
w
w
w
.exam
race.com
Cram r’s R
w
w
w
.exam
race.com
If we have equations:
w
w
w
.exam
race.com
If we have equations:
+
w
w
w
.exam
race.com
+ a
w
w
w
.exam
race.com
a
w
w
w
.exam
race.com
w
w
w
.exam
race.com
2
w
w
w
.exam
race.com
2x
w
w
w
.exam
race.com
x2
w
w
w
.exam
race.com
2 +
w
w
w
.exam
race.com
+ · · ·
w
w
w
.exam
race.com
· · ·
,
w
w
w
.exam
race.com
,1
w
w
w
.exam
race.com
1x
w
w
w
.exam
race.com
x1
w
w
w
.exam
race.com
1 +
w
w
w
.exam
race.com
+ a
w
w
w
.exam
race.com
a2
w
w
w
.exam
race.com
2,
w
w
w
.exam
race.com
,2
w
w
w
.exam
race.com
2x
w
w
w
.exam
race.com
x2
w
w
w
.exam
race.com
2 +
w
w
w
.exam
race.com
+
.
w
w
w
.exam
race.com
..
w
w
w
.exam
race.com
..
w
w
w
.exam
race.com
.
1
w
w
w
.exam
race.com
1x
w
w
w
.exam
race.com
x1
w
w
w
.exam
race.com
1 +
w
w
w
.exam
race.com
+](https://image.slidesharecdn.com/computer-science-formulas-150117013521-conversion-gate01/75/Computer-science-formulas-10-2048.jpg)