CM - elaborato RADDI

FACOLTA’ DI INGEGNERIA

Laurea Magistrale in Ingegneria Civile
I semestre – II anno
A.A. 2012 – 2013
Corso di:

Costruzioni Metalliche

Appunti di Costruzioni Metalliche

Docente:
Prof. Franco Bontempi
Assistenti:
Ing. Francesco Petrini
Ing. Pierluigi Olmati

Roma, LUGLIO 2013

Studente:
Roberto Raddi 1504138

A.A. 2012/2013

Docente: Prof. Franco Bontempi
Assistenti: Ing. Francesco Petrini

INDICE
SEZIONE 0: INTRODUZIONE
SEZIONE 1: TEORIA DELLA PLASTICITÀ
1.1 Plasticità di materiale ........................................................................................................... 3
1.1.1 Limite di plasticità................................................................................................................................. 3
1.1.2 Stati di tensione non monoassiale ....................................................................................................... 3
1.1.2.1 Superficie di scorrimento ............................................................................................................. 3
1.1.2.2 Criteri di rottura ........................................................................................................................... 3
1.1.2.3 Inrudimento ................................................................................................................................. 5
1.1.3 Legame costitutivo dell'acciaio ............................................................................................................ 6
1.1.3.1 Legame costitutivo sperimentale ................................................................................................. 6
1.1.3.2 Legame costitutivo di calcolo ....................................................................................................... 6
1.1.3.3 Legame costitutivo ciclico ............................................................................................................ 7
1.1.3 Duttilità ................................................................................................................................................. 8

1.2 Plasticità di sezione/elemento .............................................................................................. 9
1.2.1 Flessione semplice (travi) ..................................................................................................................... 9
1.2.1.1 Definizione del legame momento-curvatura .............................................................................10
1.2.1.1.1 Analisi in campo elastico ....................................................................................................10
1.2.1.1.2 Analisi in campo plastico ....................................................................................................11
1.2.1.2 Cerniera plastica .........................................................................................................................13
1.2.2 Pressoflessione (colonne)...................................................................................................................15
1.2.2.1 Analisi in campo plastico ............................................................................................................15
1.2.2.2 Analisi in campo elastico ............................................................................................................16

1.3 Plasticità di sistema ............................................................................................................ 17
1.3.1 Aspetti caratterizzanti ........................................................................................................................17
1.3.1.1 Meccanismi di collasso locale/globale - Iperstaticità .................................................................17
1.3.1.2 Ridistribuzione energie immesse dopo la plasticizzazione ........................................................17
1.3.1.3 Distribuzione dei carichi .............................................................................................................18
1.3.2 Resistenza elastoplastica del sistema strutturale ..............................................................................19
1.3.2.1 Metodo semi-analitico ...............................................................................................................19
1.3.2.1.1 Analisi elastica ....................................................................................................................19
1.3.2.1.2 Analisi elastoplastica ..........................................................................................................20
1.3.2.1.2.1 Fase di carico ..............................................................................................................20
1.3.2.1.2.2 Fase di scarico ............................................................................................................21
1.3.2.2 Metodo incrementale (push-over) .............................................................................................21
1.3.2.3 Metodo dell'analisi limite...........................................................................................................23
1.3.2.3.1 Superfici limite ...................................................................................................................23
1.3.2.3.2 Teoremi dell'analisi limite ..................................................................................................24
1.3.2.3.2.1 Teorema statico .........................................................................................................24
1.3.2.3.2.2 Teorema cinematico ..................................................................................................26
1.3.2.3.2.2.1 Trave iperstatica ................................................................................................26
1.3.2.3.2.2.1 Telaio iperstatico ...............................................................................................27

Roma, LUGLIO 2013

A.A. 2012/2013


1.4 Aspetti particolari dell'analisi plastica ................................................................................. 28
1.4.1 Comportamento ciclico della sezione inflessa ...................................................................................28
1.4.2 Influenza del taglio sul comportamento elastoplastico a flessione ...................................................29
1.4.3 Interazione tra instabilità e plasticità .................................................................................................29

SEZIONE 2: STABILITÀ DELL'EQUILIBRIO
2.1 Aspetti generali .................................................................................................................. 32
2.2 Studio del comportamento critico e post-critico di un'asta rigida ........................................ 32
2.2.1 Condizione di vincolo 1.......................................................................................................................32
2.2.1.1 Cinematica ed equilibrio ............................................................................................................33
2.2.1.1.1 Trattazione completa .........................................................................................................33
2.2.1.1.2 Linearizzazione degli spostamenti .....................................................................................33
2.2.1.1.3 Equilibrio nella configurazione indeformata......................................................................33
2.2.1.1.4 Conclusioni .........................................................................................................................33
2.2.1.2 Approccio energetico .................................................................................................................34
2.2.1.2.3 Equilibrio nella configurazione indeformata......................................................................34
2.2.1.2.4 Conclusioni .........................................................................................................................34
2.2.2.1 Cinematica ed equilibrio ............................................................................................................35
2.2.3.1 Approccio energetico .................................................................................................................36

2.3 Studio del comportamento critico e post-critico di un sistema di aste ................................. 37
2.3.1 Cinematica ed equilibrio.....................................................................................................................37
2.3.1.1 Trattazione completa .................................................................................................................37

2.4 Studio del comportamento critico e post-critico di un sistema di aste ................................. 38
2.4.1 Approccio energetico .........................................................................................................................38
2.4.1.1 Linearizzazione degli spostamenti .............................................................................................38

SEZIONE 3: CRITERI DI PROGETTAZIONE
3.1 Approccio alla progettazione .............................................................................................. 40
3.2 Conceptual design .............................................................................................................. 41
3.2.1 Performance strutturali richieste .......................................................................................................41
3.2.1.1 Rigidezza strutturale (SLE) ..........................................................................................................42
3.2.1.2 Instabilità (SLE/SLU) ...................................................................................................................42
3.2.1.3 Resistenza (SLU) .........................................................................................................................42
3.2.1.4 Duttilità (SLU) .............................................................................................................................42
3.2.2 Scelte progettuali ...............................................................................................................................42
3.2.2.1 Tipologie elementari ..................................................................................................................43
3.2.2.1.1 Concentric Braced Frames (CBF) ........................................................................................43
Roma, LUGLIO 2013

A.A. 2012/2013


3.2.2.1.2 Moment Reisting Frames (MRF) ........................................................................................43
3.2.2.1.1 ECcentric Braced Frames (EBF) ..........................................................................................44
3.2.2.2 Nodi ............................................................................................................................................44
3.2.2.2.1 Distinzione funzionale ........................................................................................................44
3.2.2.2.2 Rigidezze nodali..................................................................................................................45

3.3 Ottimizzazione.................................................................................................................... 48
3.3.1 Ottimizzazione per livelli ....................................................................................................................48
3.3.1.1 Sizing...........................................................................................................................................48
3.3.1.2 Morfologica ................................................................................................................................49
3.3.1.3 Topologica ..................................................................................................................................49
3.3.1.4 Introduzione della sottostruttura ..............................................................................................50
3.3.1.4.1 Uso dell'Outrigger ..............................................................................................................50
3.3.2 Ottimizzazione per risposta ................................................................................................................51
3.3.2.1 Assiale.........................................................................................................................................51
3.3.2.1.1 Principi cardine...................................................................................................................51
3.3.2.1.1.1 Trazione......................................................................................................................51
3.3.2.1.1.2 Compressione ............................................................................................................51
3.3.2.1.2 Aspetti tecnologici..............................................................................................................52
3.3.2.1.2.1 Buckling Restrained Braced Frame ............................................................................52
3.3.2.1.2.2 Trussed Tube ..............................................................................................................53
3.3.2.2 Flessionale ..................................................................................................................................54
3.3.2.2.1 Risposta strutturale ............................................................................................................54
3.3.2.2.2 Aspetti tecnologici..............................................................................................................55
3.3.2.2.2.1 Outrigger in sommità .................................................................................................55
3.3.2.2.2.2 Irrigidimenti strutturali ..............................................................................................55

SEZIONE 4: PROGETTAZIONE IN ZONA SISMICA
4.1 Introduzione ....................................................................................................................... 57
4.2 Metodo dissipativo semplificato ......................................................................................... 57
4.2.1 Duttilità locale ....................................................................................................................................58
4.2.1.1 Materiale ....................................................................................................................................58
4.2.1.2 Sezione .......................................................................................................................................58
4.2.2 Fattore di struttura (q) .......................................................................................................................59
4.2.2.1 Indice di duttilità (q0)..................................................................................................................60
4.2.2.2 Fattore di regolarità strutturale (KR) ..........................................................................................61
4.2.2.3 Fattore di duttilità locale (KD) .....................................................................................................62
4.2.3 Gerarchia delle resistenze ..................................................................................................................63

APPENDICE A: COLLASSO PROGRESSIVO ................................................................................... 66
APPENDICE B: FATICA ............................................................................................................... 68
APPENDICE C: MODELLAZIONE DI DETTAGLIO........................................................................... 70

Roma, LUGLIO 2013

A.A. 2012/2013

SEZIONE 0


INTRODUZIONE
1) Nell'ambito delle costruzioni civili, le strutture portanti di un qualsiasi organismo
sono prevalentemente realizzate, oltre che in cemento armato, impiegando
materiali metallici:si tratta soprattutto di acciai da carpenteria e solo di recente
sono state introdotte leghe leggere, tradizionalmente in uso nell'industria
aeronautica.
2) Il comportamento meccanico delle strutture metalliche è fortemeente
condizionato dalle proprietà del materiale acciaio, che presenta buona resistenza a
trazione quanto a compressione, oltre ad elevata resistenza, tenacità ed
adattabilità plastica.
3) Tra i principali vantaggi connessi all'impiego di strutture metalliche si possono
annoverare:
• Semplicità e maggiore affidabilità di modellazione: in fase di calcolo
strutturale, il comportamento statico delle membrature in acciaio non
risente delle incertezze di esecuzione. Le schematizzazioni teoriche
possono sufficientemente adattarsi alla struttura reale sia per le
caratteristiche fisico meccaniche sia per le modalità di esecuzione delle
unioni, dei collegamenti e dei vincoli. Questi aspetti si riflettono
nell'impiego di coefficienti di sicurezza più bassi e quindi meno
penalizzanti rispetto a quelli relativi, per esempio, al cemento armato.
• Rapidità di esecuzione: il procedimento costruttivo prevede una prima
fase di produzione degli elementi strutturali, che si volge in officina sotto il
diretto controllo delle maestranze specializzate mentre in cantiere si
realizza il montaggio mediante il collegamento tra gli elementi già
prodotti. In questo modo la costruzione non risente delle condizioni
stagionali che bloccano i procedimenti "a umido" come nel caso delle
costruzioni murarie e di c.a. e risulta conseguentemente più rapida.
• Re-impiego: accanto alla riduzione dei tempi descritta, si rileva la
possibilità di trasformazione delle strutture, intesa sia come ampliamento
della stessa per variazioni funzionali dell'opera, sia come intervento di
rinforzo richiesto da deficienze statiche conseguenti ad una modifica dello
schema statico originario e/o dei carichi di esercizio.
• Elevato grado di efficienza: il rapporto tra la resistenza meccanica
(espressa in termini di massima tensione di calcolo) ed il peso specificoè,
per i materiali metallici, molto elevato e sempre superiore a quello degli
altri materiali da costruzione tradizionali. Questo aspetto si traduce nella
possibilità di impiegare elementi strutturali di dimensione ridotte e quindi
di peso minore. A questo si accompagna dunque un più razionale uso degli
spazi per il minore ingombro degli elementi portanti ed un minore
impegno per le strutture di fondazione, soggette a carichi più bassi.
• Ottima risposta alle azioni dinamiche: questo giustifica l'ampio utilizzo di
acciaio nelle costruzioni industriali e nei ponti in zona sisimica

Roma, LUGLIO 2013

Pagina 1

A.A. 2012/2013


4) Per contro si annoverano alcuni svantaggi che penalizzano l'uso generalizzato del
materiale acciaio:
• Instabilità, sia locale che globale , conseguente proprio all'aumentata
snellezza delle membrature, che diventa uno degli aspetti più significativi
in fase di verifica dell'elemento e dell'insieme della struttura metallica.
• Elevata deformabilità: che non consente di sfruttare appieno le capacità
resistenti e pone problemi sia di instabilità che di funzionalità dell'opera.
Proprio per questa ragione si impongono delle limitazioni, oltre che sulle
tensioni, anche sulle deformazioni.
• Degrado per corrosione: il materiale acciaio è particolarmente sensibile
all'attacco di agenti atmosferici che lo ossidano; pertanto è necessaria una
costante manutenzione.
• Vulnerabilità considerevole nei confronti del fuoco: per le strutture
metalliche si registra una rapida diminuzione delle caratteristiche di
resistenza al crescere della temperatura e questo comporta particolare
cura nei confronti degli accorgimenti da adottare ai fini della protezione
degli elementi portanti.
5) Emerge, sin da queste considerazioni iniziali, che la corretta progettazione di
strutture metalliche, le quali abbracciano tutti i settori delle costruzioni (edilizia
civile e industriale, ponti e grandi coperture, torri e pali di sostegno per
elettrodotti,serbatoi e costruzioni marittime) non può prescindere dalla
conoscenza di queste problematiche. La costruzione metallica, inoltre si adatta
particolarmente alle tecniche di produzione in serie dalle quali viene condotto ad
una prefabbricazione industrializzata sempre più spinta.
6) Infine le moderne tecnologie danno la possibilità di introdurre nelle strutture dei
materiali con caratteristiche di resistenza differenziate, con la creazione della
cosiddetta quarta dimensione, che si accompagna alle tre geometriche, che
fornisce alla progettazione un ulteriore elemento di scelta. Quindi per il continuo
miglioramento dei materiali ed il graduale incremento dell'industrializzazione le
strutture metalliche presentano notevoli prospettive di sviluppo.

Roma, LUGLIO 2013

Pagina 2

A.A. 2012/2013

SEZIONE 1

TEORIA DELLA PLASTICITA'
A

1.1
1.1.1

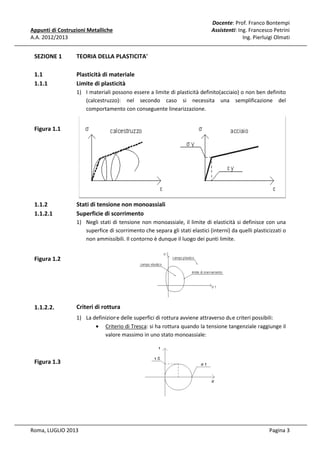
Docente Prof. Franco Bontempi
e:

Plasticità di ma
ateriale
Limite di plasti
icità
1) I materiali po
ossono essere a limite di plasticità definito(acciai o non ben definito
aio)
(calcestruzzo
o): nel secondo caso si necessita una semplificazione del
a
comportame
amento con conseguente linearizzazione.

Figura 1.1

1.1.2
1.1.2.1

Stati di tension non monoassiali
ne
Superficie di sc
corrimento
1) Negli stati di tensione non monoassiale, il limite di elasticit si definisce con una
tà
superfice di scorrimento che separa gli stati elastici (interni) da quelli plasticizzati o
s
non ammissi
ibili. Il contorno è dunque il luogo dei punti limite
e.

Figura 1.2

1.1.2.2.

Criteri di rottur
ra
1) La definizione delle superfici di rottura avviene attraverso due criteri possibili:
• Crite di Tresca: si ha rottura quando la tensione tan
erio
angenziale raggiunge il
valor massimo in uno stato monoassiale:
re

Figura 1.3

Roma, LUGLIO 2013

Pagina 3


A.A. 2012/2013
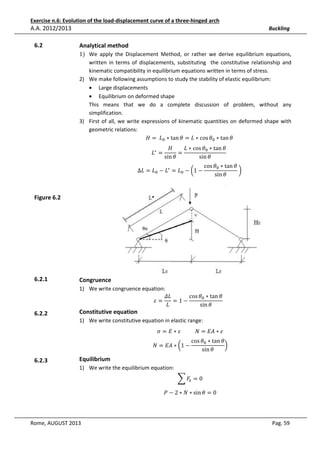
dove:

•

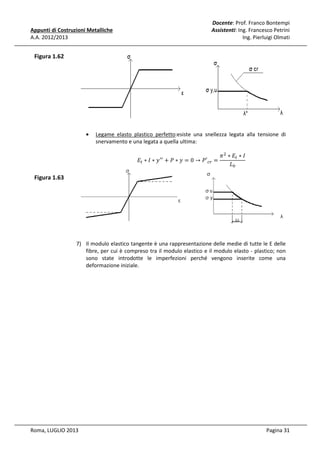
1
∗ max ሼሾߪଵ − ߪଶ ሿ; ሾߪଶ − ߪଷ ሿ; ሾߪଷ − ߪଵ ሿሽ
2
1
߬௦ = ∗ max (ߪଵ , ߪଶ , ߪଷ )
2
Criterio di Von Mises: si ha rottura quando ߬̅ = ߬௦ dove la ߬̅ è per
ഥ
definizione la media delle tensioni tangenziali agenti su una sfera di raggio
piccolo tendente a zero con il centro coincidente con il punto in esame.
߬௠௔௫ =

Figura 1.4

dove:

߬̅ =

Figura 1.5

߬̅ = ඨ

√15
1

∗ ඥ[ሺߪଵ − ߪଶ ሻଶ + ሺߪଶ − ߪଷ ሻଶ + ሺߪଷ − ߪଵ ሻଶ ]

2) Confrontando i due criteri:

Roma, LUGLIO 2013

ଶగ
గ
1
ଶ
න ݀ߙ ∗ න ߬௡ ∗ sin ߚ ∗ ݀ߚ
4∗ߨ ଴
଴

߬௦ =

1
∗ max (ߪଵ , ߪଶ , ߪଷ )
2

Pagina 4


A.A. 2012/2013

1.1.2.3

Incrudimento
1) Si riporta uno schema riassuntivo e i relativi diagrammi delle possibile situazioni:

Figura 1.6
Incrudimento

Isotropia

Staticità

Incrudimento
isotropo

Incrudimento
non isotropo

(la superficie
cambia le
dimensioni, non la
forma)

(la superficie
cambia le
dimensioni e la
forma)

(1)

(2)

Incrudimento
statico

Incrudimento
cinematico

(la superficie
non si sposta)

(la superficie si
sposta)

(3)

(4)

Figura 1.7

Roma, LUGLIO 2013

Pagina 5

A.A. 2012/2013

1.1.3
1.1.3.1


Legame costitutivo dell'acciaio
Legame costitutivo sperimentale
1) Da una prova di trazione monoassiale, viene derivato il legame costitutivo
dell'acciaio riportando la tensione di trazione in funzione della deformazione
registrata fino alla rottura del provino:

Figura 1.8

Figura 1.9

1.1.3.2

Legame costitutivo di calcolo
1) E' possibile modellare il comportamento dell'acciaio secondo differenti legami più
o meno semplificati, associando ad ognuno un modello reologico esplicativo:
• Rigido perfettamente plastico: il modello reologico è quello di un blocco a
cui è applicata una forza F. Il comportamento è descritto da 1 parametro
indipendente.

Figura 1.10

Roma, LUGLIO 2013

Pagina 6

A.A. 2012/2013


•

Elastoplastico perfetto: Il modello reologico è quello di un blocco cui è
applicata una forza F attraverso una molla di rigidezza E. Il comportamento
è descritto da 3 parametri indipendenti.

•

Elastoplastico incrudente: il modello reologico è quello di un blocco
vincolato mediante una molla di rigidezza E1 e sollecitato da una forza F
attraverso un'altra molla di rigidezza E0. Il comportamento è descritto da 4
parametri indipendenti, dei quali la pendenza del ramo incrudente si
valuta con il criterio energetico.

•

Elastoplastico incrudente con tratto a deformazioni libere: il modello
reologico è quello di un blocco sollecitato da una forza F attraverso una
molla di rigidezza E0 e vincolato da un'altra molla di rigidezza E1 che si
attiva solo una volta raggiunto un certo livello di spostamento.

Figura 1.11

Figura 1.12

Figura 1.13

1.1.3.3

Legame costitutivo ciclico
1) Dai legami costituivi di calcoli definiti nel paragrafo precedente, è possibile
derivare i corrispondenti descrittivi, però, di un comportamento ciclico. Tale
aspetto è di particolare rilevanza per effettuare con efficacia le analisi dinamiche
che sono necessarie per l'analisi sismica:

Roma, LUGLIO 2013

Pagina 7

A.A. 2012/2013


Figura 1.14

2) Un'altro legame costitutivo per comportamento ciclico è quello di Menegotto
Pinto, descritto dalla relazione:
ߪ
ߝ
ߝ
ߝ
ߝ ௡ ଵ/௡
ሺ1 − ܾሻ ∗ ൬ ൰ / ൤1 + ൬ ൰ ൨
= ܾ∗൬ ൰+݀ = ݀∗൬ ൰+
ߝ଴
ߝ଴
ߝ଴
ߝ଴
ߪ଴

Figura 1.15

1.1.4

Duttilità
1) La duttilità è una proprietà fisica della materia che indica la capacità di un corpo o
di un materiale di deformarsi plasticamente sotto carico prima di giungere
arottura, cioè la capacità di sopportare deformazioni plastiche. Un corpo è tanto
più duttile quanto maggiore è la deformazione raggiunta prima della rottura.

Figura 1.16

Roma, LUGLIO 2013

Pagina 8

A.A. 2012/2013

1.2
1.2.1


Plasticità di sezione/elemento
Flessione semplice (travi)
1) Per trave si intende un elemento strutturale con una dimensione predominante,
atto a trasferire una sollecitazione tendenzialmente trasversale al proprio asse
geometrico lungo tale asse, dalle sezioni investite dal carico fino ai vincoli, che
garantiscono l'equilibrio esterno della trave assicurandola al contesto circostante.
E' valida la teoria di De Saint-Venant.
2) Le ipotesi di calcolo preliminari sono:
• Conservazione delle sezioni piane
• Piccoli spostamenti (si prescinde dalla stabilità)
• Legame elastoplastico perfetto
3) Si rappresenta l'andamento delle tensioni nella sezione all'aumentare del
momento flettente agente, in modo da evidenziare il passaggio al campo plastico:

Figura 1.17

4) E' possibile definire il fattore di forma β come rapporto tra il momento di
plasticizzazione Mp è quello di snervamento My. Tale grandezza è un indice delle
risorse plastiche dell'elemento e distingue due possibili comportamenti:
• β=1 Comportamento elastoplastico perfetto

Figura 1.18

•

β>1 Comportamento elastoplastico incrudente

Figura 1.19

Roma, LUGLIO 2013

Pagina 9


A.A. 2012/2013

1.2.1.1

Definizione del legame Momento-Curvatura
1) Si consideri un concio di trave di lunghezza l unitaria inflesso secondo un raggio R:

Figura 1.20

2) L'obiettivo è valutare lo stato tensionale dell'elemento al variare del
comportamento. Si prende in esame la fibra tesa a-b:
‫ݎ‬
‫ ݕ + ݎ‬
‫ݕ+ݎ‬
‫ݕ+ݎ‬
=
→ ‫= ݎ‬
→ ‫= ݎ‬
෢
෢
1 + ߝ(‫)ݕ‬
1 + ߝ(‫)ݕ‬
ܾܽ
ܿ݀
1
ߝሺ‫ݕ‬ሻ = ‫ܽݎݑݐܽݒݎݑܿ = ߯ ߯ ∗ ݕ‬
‫ݎ‬

1.2.1.1.1

Analisi in campo elastico
1) Esiste una diretta proporzionalità tra tensione e deformazione secondo le
relazioni:
ߪሺ‫ݕ‬ሻ = ‫ߝ ∗ ܧ‬ሺ‫ݕ‬ሻ = ‫߯ ∗ ݕ ∗ ܧ‬
ெ
→ ߯=
ቊ
ெ
ாூ
ߪሺ‫ݕ‬ሻ = ∗ ‫ݕ‬
ூ

2) Alla linearità tensione-deformazione, corrisponde dunque una linearità tra
momento e curvatura:
‫ ݕܯ‬ℎ
ߪሺ‫ݕ‬ሻ =
∗ → ‫ܯ‬௬ = ߪ௬ ∗ ܹ
‫2 ܫ‬
߯௬ =

Roma, LUGLIO 2013

‫ܯ‬௬ ߪ௬ ∗ ܹ ‫ߝ ∗ ܧ‬௬ ∗ ܹ 2 ∗ ߝ௬
=
=
=
‫ܫܧ‬
‫ܫܧ‬
‫ܫܧ‬
ℎ

Pagina 10


A.A. 2012/2013

1.2.1.1.2

Analisi in campo plastico
1) Considerando il limite di snervamento, superato il limite elastico, non c'è più
diretta proporzionalità tra tensione e deformazione e lo stato tensionale rimane
costante all'aumentare della deformazione:

Figura 1.21

La plasticizzazione si diffonde dalle fibre esterne a massima deformazione verso l'asse
neutro con un nucleo elastico che si riduce di ampiezza all'aumentare del momento
esterno e per il quale vale il legame elastico trovato precedentemente.
2) Il diagramma tensionale elastoplastico della sezione può essere scomposto come
segue in modo da poter ricavare l'andamento del diagramma momento-curvatura
in campo plastico:

Figura 1.22

߯௬
2 ∗ ‫ݕ‬௘
=
; ‫ܯ‬௣ = ߪ௬ ∗ ܼ ; ‫ߪ ∗ ܹ = ܯ‬௬ + ܼ ∗ ߪ௬ − ܼ௘ ∗ ߪ௬
௘
߯௘௣
ℎ

4) Considerando:

Dove Z è il modulo plastico, We è il modulo elastico del nucleo elastico e Ze è il
modulo plastico del nucleo elastico.
ߪ௬ ∗ ܹ ‫ܯ‬௣ ߪ௬ ∗ ܼ݁ ‫ܯ‬௣ ߪ௬ ∗ ܹ
ߪ௬ ∗ ܼ݁
‫ܯ‬
=
+
−
=
∗ቈ
+1−
቉
‫ܯ‬௬
‫ܯ‬௬
‫ܯ‬௬
‫ܯ‬௬
‫ܯ‬௬
‫ܯ‬௣
‫ܯ‬௣

Sapendo che ߚ =

ெ೛
ெ೤

e ܼ=

ெ೛
ఙ೤

:

ܼ݁ − ܹ
‫ܯ‬
ܼ݁
ܹ
௘
௘
= ߚ ∗ ൤ + 1 − ൨ = ߚ ∗ ൤1 −
൨
‫ܯ‬௬
ܼ
ܼ
ܼ

Sia We che Ze dipendono dalla forma del nucleo elastico; essendo ‫ݕ‬௘ = ‫ݕ‬௘ ൫߯௬ , ߯௘௣ ൯
si ha

Roma, LUGLIO 2013

ெ
ெ೤

೤
= ߚ ∗ ߶ ቀ ఞ ቁ quindi:

ఞ

Pagina 11


A.A. 2012/2013

‫ܯ‬
‫߯∗ܫ∗ܧ‬
߯
‫߯∗ܫ∗ܧ= ܯ‬
=
=
൜‫ → ߯ ∗ ܫ ∗ ܧ = ܯ‬
௬
௬
‫ܯ‬௬ ‫߯ ∗ ܫ ∗ ܧ‬௬ ߯௬

Si studiano questi comportamenti su un elemento di sezione rettangolare.
Noto che:
1 ܾ ∗ ℎଷ 1
= ∗ ܾ ∗ ℎଶ
ܹ=
6
12 ℎ
2
1 ܾ ∗ (2 ∗ ‫ݕ‬௘ )ଶ 2
ܹ =
= ∗ ܾ ∗ ‫ݕ‬௘ ଶ
௘
‫ݕ‬௘
12
3
ܹ =ܾ∗
௘

ܼ௘ =
Si può scrivere:

ℎ ℎ
ℎଶ
∗ =ܾ∗
2 2
4

ܾ ∗ (2 ∗ ‫ݕ‬௘ )ଶ
= ܾ ∗ ‫ݕ‬௘ ଶ
4

‫ܯ‬௣
‫ܯ‬
ܼ݁ − ܹ
௘
=
∗ ൤1 −
൨
ܼ
‫ܯ‬௬ ‫ܯ‬௬

Dato che per sezioni rettangolari ߚ =

ெ೛
ெ೤

௓

ଷ

= ௐ = ଶ , sostituendo alla precedente,

abbiamo:

2
ଶ
ܾ ∗ ‫ݕ‬௘ ଶ − ∗ ܾ ∗ ‫ݕ‬௘ ଶ
3
3
1
‫ݕ‬௘ ଶ
3
1
߯
‫ܯ‬
3
= ∗ ቎1 −
቏ = ∗ ൤1 − ∗ ቀ2 ∗ ቁ ൨ = ∗ ൥1 − ∗ ቆ ቇ ൩
ℎଶ
2
3
2
3
߯௬
‫ܯ‬௬ 2
ℎ
ܾ∗
4

5) Si è giunti dunque a scrivere la relazione nella forma:

߯௬
‫ܯ‬
= ߚ∗߶൬ ൰
‫ܯ‬௬
߯
da questa relazione si ottiene il diagramma del legame costitutivo tra il momento
e la curvatura, il quale presenta un andamento di tipo lineare nel campo elastico e
non lineare nel campo plastico.

Figura 1.23

Roma, LUGLIO 2013

Pagina 12

A.A. 2012/2013


5) Applicando la stessa analisi per sezioni a geometrie diverse si ottiene una
variazione del coefficiente ߚ, in particolare questo diminuisce al aumentare del
valore di W della sezione.

Figura 1.24

1.2.1.2

Cerniera plastica
1) L'ingresso in campo plastico dell'elemento corrisponde al raggiungimento del
momento massimo pari a quello di plasticizzazione in un tratto di lunghezza Δl, di
entità stimabile:
‫ܯ‬௬
‫ܯ‬௣
‫ܯ‬௣
‫ܮ‬
‫)1 − ߚ( ∗ ܮ‬
=
→ ߚ =
=
→ ∆‫= ܮ‬
‫ܮ‬
‫ ܮ‬Δ‫ܮ‬
ߚ
‫ܯ‬௬ ‫ܮ∆ − ܮ‬
2
2− 2
2) Per una sezione IPE, β è pari circa a 1,14 quindi la zona di plasticizzazione ha una
lunghezza pari al 10% della lunghezza totale della trave e può essere quindi
assimilata ad un punto.
3) In tale punto, la sezione è sollecitata dal momento di plasticizzazione quindi non
reagisce più e diventa una cerniera plastica.

Figura 1.25

4) E' possibile dunque realizzare un diagramma momento-curvatura che rappresenta
l'equivalente a livello di sezione del diagramma tensione-deformazione definito a
livello di materiale. Tale parallelismo è riassunto nella tabella seguente:

Roma, LUGLIO 2013

Pagina 13


A.A. 2012/2013

ߪ௬

Parametri

Materiale

Elemento

Tensionali

ߝ௬ , ߝ௨
ߝ௨
ߤ଴ =
ߝ௬

M
߯௬ , ߯௨
߯௨
ߤଵ =
߯௬

Deformativi
Duttilità

2 ∗ ߝ௬
ℎ
ߝ௬ = ߯௬ ∗ → ߯௬ =
ℎ
2

ℎ
2 ∗ ߝ௨
ߝ௨ = ߯௨ ∗ → ߯௨ =
ℎ
2
6) Si riporta, infine, la procedura per il tracciamento del diagramma momento
curvatura:

Fisso valore χ'

Figura 1.26

Ricavo diagramma
ε'=χ'*y
Legame costitutivo

Ricavo diagramma σ'

Ricavo la corrispondente M'

NO

Roma, LUGLIO 2013

Numero di punti
sufficiente?

SI

Tracciamento
(M',χ')

Pagina 14


A.A. 2012/2013

1.2.2
1.2.2.1

Pressoflessione (colonne)
Analisi in campo plastico
1) Il concetto di cerniera plastica può essere esteso alle sollecitazioni composte
studiando l'interazione tra sforzo normale e momento flettente in ipotesi di
validità della teoria di De Saint-Venant.
2) L'obiettivo è individuare nel piano M-N la superficie limite a plasticizzazione
ovvero il luogo dei punti che genera la prima plasticizzazione della sezione.
3) Si analizza come di consueto la risposta tensionale della sezione all'aumentare del
momento flettente:

Figura 1.27

Si può scomporre tale diagramma:

Figura 1.28

4) Mediante le consuete relazioni si giunge all'espressione del dominio plastico:
ܰ = 2ܾ ߪ଴ ݀
ܾ
‫݅ݐ݊݁݃ܽ ݅݊݋݅ݖܽݐ݈݈݅ܿ݁݋ݏ‬
൝
‫ߪ = ܯ‬௬ (ℎଶ − 4݀ ଶ )
4

‫ۓ‬
ۖ

ܰ௣ = ܾ ߪ଴ ݀
ቐ
ܾ ℎଶ ‫݁݊݋݅ݖܽݖݖ݅ܿ݅ݐݏ݈ܽ݌ ݅݀ ݅݊݋݅ݖܽݐ݈݈݅ܿ݁݋ݏ‬
‫ܯ‬௣ = ߪ௬
4

ܰ
= 2 ‫ݕ‬଴ ℎ
ܰ௣

ܰ
‫ܯ‬
= 1 − ቆ ቇ ݁‫݋݉݅ݐ݈ݑ ݋݅݊݅݉݋݀ ݁݊݋݅ݖܽݑݍ‬
ଶ →
2‫ݕ‬଴
ܰ௣
‫ܯ‬௬
‫ܯ۔‬
ۖ‫ − 1 = ܯ‬൬ ℎ ൰
‫ ە‬௣

Roma, LUGLIO 2013

ଶ

Pagina 15


A.A. 2012/2013

1.2.2.2

Analisi in campo elastico
1) La stessa procedura per la definizione del dominio ultimo può essere condotta
considerando un legame elastico del materiale:

Figura 1.29

2) Le relazioni, come precedentemente:

ܾℎଶ
ߪ′
6
‫݅ݐ݊݁݃ܽ ݅݊݋݅ݖܽݐ݈݈݅ܿ݁݋ݏ‬
൞
2‫ݕ‬௢
ᇱ
ܰ = ܾ ℎ ߪ (1 +
− 1)
ℎ
‫=ܯ‬

ܾℎଶ
2‫ݕ‬௢
൬1 +
൰ ߪ′
6
ℎ
‫݋ݐ݊݁݉ܽݒݎ݁݊ݏ ݅݀ ݅݊݋݅ݖܽݐ݈݈݅ܿ݁݋ݏ‬
2‫ݕ‬௢
‫۔‬
‫ܰ ە‬௬ = ܾ ℎ ൬1 + ℎ ൰ ߪ′
‫ܯۓ‬௬ =

‫ܯ‬
1 1 ܰ
ܰ
‫ܯ‬
= 1 − ቆ ቇ →
= − ቆ ቇ ݁‫݋݉݅ݐ݈ݑ ݋݅݊݅݉݋݀ ݁݊݋݅ݖܽݑݍ‬
‫ܯ‬௣ ߚ ߚ ܰ௣
‫ܯ‬௬
ܰ௬
ଶ

3) Si possono confrontare i due domini, individuando la duttilità dell'elemento come
distanza tra i due lungo una retta passante per l'origine.

Figura 1.30

Roma, LUGLIO 2013

Pagina 16

A.A. 2012/2013

1.3


Plasticità di sistema
1) Per definire la plasticità di sistema si necessita di alcune definizioni preliminari:
• Duttilità di struttura: rapporto tra lo spostamento ultimo di collasso e
quello di primo snervamento
• Collasso strutturale: trasformazione della struttura in un cinematismo
all'incremento del carico agente, data la formazione di cerniere plastiche.

1.3.1
1.3.1.1

Aspetti caratterizzanti
Meccanismi collasso locale/globale - Iperstaticità
1) Dato un sistema n volte iperstatico, la formazione del cinematismo avviene alla
formazione di n+1 cerniere plastiche all'aumentare del carico agente.
2) Ne deriva che si distingueranno collassi locali, che compromettono uno solo degli
elementi strutturali ma non rendono la struttura un cinematismo, dal collasso
globale che si ha alla formazione della cerniera successiva a quella che ha reso la
struttura isostatica.

Figura 1.31

1.3.1.2

Ridistribuzione energie immesse dopo la plasticizzazione
1) Si consideri una trave doppiamente incastrata (iperstaticità flessionale pari a 2),
sottoposta ad un carico uniformemente distribuito crescente. Il momento di
reazione degli incastri cresce all'aumentare del carico esterno fino al limite di
snervamento, arrivati al quali si ha la formazione contemporanea di due cerniere
plastiche all'estremità (il momento non può più aumentare) e lo schema statico
diventa quello di trave appoggiata.

Figura 1.32

Roma, LUGLIO 2013

Pagina 17

A.A. 2012/2013


2) Ne consegue che un ulteriore aumento dei carichi può essere equilibrato solo da
un aumento del momento in mezzeria fino a che anche in quella sezione si
raggiunge il limite plastico con la formazione della terza cerniera che rende la
struttura un cinematismo.

Figura 1.33

Figura 1.34

3) Per ridistribuzione delle energie immesse si intende,quindi, proprio la modifica
della risposta strutturale in termini di sollecitazioni equilibranti il carico esterno
dovuta al raggiungimento del limite plastico in alcuni punti discreti.

1.3.1.3

Distribuzione dei carichi
1) Rispetto all'esempio precedente, si considera la trave doppiamente incastrata
sollecitata da un carico concentrato in mezzeria crescente.

Figura 1.35

2) In questo caso non abbiamo ridistribuzione del momento flettente perchè
all'aumentare del carico si formano contemporaneamente le tre cerniere
plastiche.

Figura 1.36

Roma, LUGLIO 2013

Pagina 18


A.A. 2012/2013

1.3.2
1.3.2.1

Resistenza elastoplastica del sistema strutturale
Metodo semi-analitico
1) Si tratta di un metodo che ci permette di trovare soluzioni in forma chiusa a tratti.
Ne segue un'applicazione ad un semplice schema statico formato da tre aste
incernierate che formano un sistema di iperstaticità pari a 1.

Figura 1.38

1.3.2.1.1

Analisi elastica
1) Utilizzando il metodo degli spostamenti, si scrive la congruenza e impongo
l’equilibrio. Ciò equivale ad assegnare lo spostamento δ per determinare lo sforzo
assiale nelle tre aste. Imponendo:
• X = sforzo assiale in asta 1
• Y = sforzo assiale in aste 2, 3
2) Si scrive l'equazione di congruenza per l'asta 1
ߜ = ݈ ∗ ߝ = ݈ ∗ = ݈ ∗ → ܺ =
ா
ா஺
ఙ

௑

ா஺ఋ
௟

Si passa alle aste 2, 3 (ipotesi di piccoli spostamenti ߜ ′ = ߜ ∗ cos ,)
గ
ସ

ߨ
ߜ cos 4
∆݈
ܻ
ܻ
‫ܣܧ‬
ߨ ‫ߜܣܧ‬
ߝ= =
→
=
→ ܻ =
∗ ߜ ∗ cosଶ =
݈
݈
‫ܣܧ‬
‫ܣܧ‬
݈
4
2݈
ߨ
cos 4

Si impone X=2Y e quindi l’equilibrio:
ቊ

ߨ
=ܲ
4
ܺ =2∗ܻ

ܺ + 2 ∗ ܻ ∗ cos

ܲ
ܲ
‫= ܻۓ‬
ߨ = 2 + √2
ۖ
2 ∗ ቂ1 + cos 4 ቃ
ܲ
2ܲ
‫=ܺ ۔‬
ߨ = 2 + √2
ۖ
ቂ1 + cos 4 ቃ
‫ە‬

Si determina il carico limite elastico e la corrispondente deformazione limite:
ܺ௘௟ =

Roma, LUGLIO 2013

2 + √2
2ܲ

= ߪ௬ ∗ ‫ܲ → ܣ‬௘௟ =

2 + √2
݈ ∗ ܺ௘௟ ݈ ∗ ߪ௬
∗ ߪ௬ ∗ ‫ߜ → ܣ‬௘௟ =
=
2
‫ܣܧ‬
‫ܧ‬
Pagina 19


A.A. 2012/2013

1.3.2.1.2
1.3.2.1.2.1

Analisi elastoplastica
Fase di carico
1) Prescindendo dallo studio dell'asta 1, il cui sforzo assiale rimane costante, si scrive
l'equilibrio:
ܺ = ߪ௬ ∗ ‫ݐݏ݋ܿ = ܣ‬
ܲ − ߪ௬ ∗ ‫ܣ‬
ߨ
→ ܻ =
൝
2 ∗ ܻ ∗ cos = ܲ = ܿ‫ݐݏ݋‬
√2
4
2) Si determina il carico di plasticizzazione per le aste 2 e 3 e poi la sovraresistenza:
ܻ = ߪ௬ ∗ ‫= ܣ‬

ܲ௖௥ − ߪ௬ ∗ ‫ܣ‬
√2

→ ܲ௖௥ = ߪ௬ ∗ ‫ ∗ ܣ‬൫1 + √2൯

1 + √2
ܲ௖௥ ߪ௬ ∗ ‫ ∗ ܣ‬൫1 + √2൯ 1 + √2 1 + √2
=
=
=
= √2 ∗
= √2
ܲ௘௟
2 + √2
2 + √2
1 + √2
√2
1+ 2
2 ∗ ߪ௬ ∗ ‫ܣ‬
2

Il valore √2 comporta che grazie all’entrata in campo plastico si ottiene circa un
40% in più di resistenza.
3) Si valuta la duttilità:
ߨ
ߜ ∗ cos 4
ܻ
ܻ
∆݈
→
=
ߝ= =
݈
‫ܣܧ‬
‫ܣܧ‬
݈
ߨ
cos 4

4) Ponendo P=Pcr si ottiene lo spostamento critico, da cui la duttilità:
ߜ௖௥ =

ߪ௬ ∗ ‫ܣ‬
ߪ௬ ∗ ݈
2 ∗ ߪ௬ ∗ ݈
݈
∗
ଶ → ߜ௖௥ =
ߨ =
‫ܣܧ‬
‫ܧ‬
cosଶ ቀ ቁ
√2
4
‫∗ܧ‬ቆ 2 ቇ
ߤ=

‫ܧ‬
ߪ௖௥ 2 ∗ ߪ௬ ∗ ݈
=
∗
=2
ߪ௬ ∗ ݈
ߪ௘௟
‫ܧ‬

5) Sebbene, dunque, la duttilità di materiale sia stata supposta infinita, quella della
struttura è pari solamente a due, quindi la struttura collassa per formazione delle
cerniere plastiche.

Figura 1.39

Roma, LUGLIO 2013

Pagina 20


A.A. 2012/2013

1.3.2.1.2.2

Fase di scarico
1) Si suppone di annullare la forza agente sul sistema, quindi le aste 2,3 tenderebbero
a tornare nella posizione iniziale contrastate, però, dalla deformazione residua
dell'asta 1 plasticizzata. Ne consegue, per la congruenza, che l'asta 1 risulta
compressa mentre la 2 e la 3 tese.
2) Supponendo un comportamento di scarico uguale a quello di carico si possono
valutare le entità degli sforzi assiali in fase elastica e gli sforzi residui:

‫= ܺۓ‬

ܺ
൜ ௥௘௦
ܻ௥௘௦

1.3.2.2

∆ܲ = −ܲ௘௟ = −ߪ௬ ∗ ‫ ∗ ܣ‬൫1 + √2൯
‫= ܺ∆ۓ‬

2 + √2
2 + √2
→
݂ܽ‫ܽܿ݅ݐݏ݈ܽ݁ ݁ݏ‬
ܲ
‫= ܻ۔‬
‫ܲ∆ = ܻ∆۔‬
‫ە‬
‫ە‬
2 + √2
2 + √2
2ܲ

2 ∗ ∆ܲ

‫ ∗ ܣ ∗ ߪ− = ܺۓ‬ቆ √2 ቇ
௬
ۖ ௥௘௦
= ܺ௖௥ − ∆ܺ
2 + √2 ‫݅ݑ݀݅ݏ݁ݎ ݅ݖݎ݋݂ݏ‬
→
= ܻ௖௥ − ∆ܻ
1
‫۔‬
൰
ۖ ܻ௥௘௦ = ߪ௬ ∗ ‫ ∗ ܣ‬൬
2 + √2
‫ە‬

Metodo incrementale (push-over)

1) L'analisi di pushover è un metodo di analisi statica non lineare che consiste nello
nell'applicare alcune distribuzioni di forze via via crescenti sulla struttura, in modo
da studiare la sua risposta in termini elastoplastici fino al collasso globale o locale
2) Si riporta un esempio di analisi di pushover su un portale incastrato caricato da
due forze concentrate orizzontali e verticali che sono incrementate
proporzionalmente attraverso un coefficiente λ
.

Figura 1.40

3) Al raggiungimento in una sezione del limite plastico, si ha una formazione di una
cerniera con variazione dello schema statico sui quali agiscono i successivi
incrementi di carico fino al collasso.
Roma, LUGLIO 2013

Pagina 21

A.A. 2012/2013


Figura 1.41

4) Il problema elastoplastico è risolto dunque come una successione di problemi
elastici caratterizzati ognuno da un carico maggiorato di λ. in riferimento
all'esempio riportato i valori di λ per ogni schema di carico:
• 1° schema: 0<λ<22.5
• 2° schema: 22.5<λ<28
• 3° schema: 28<λ<28.7
• 4° schema: 28.7<λ<31.5
da cui si evince che λy=22.5 e λcr=31.5
5) La configurazione deformata possibile è la seguente

Figura 1.42

E' possibile rappresentare l'andamento della deformazione in funzione di λ
ottenendo una spezzata (successione stati elastici)

Figura 1.43

Roma, LUGLIO 2013

Pagina 22

A.A. 2012/2013

1.3.2.3


Metodo dell'analisi limite
1) Il metodo dell'analisi limite è un metodo energetico per il calcolo del moltiplicatore
critico dei carichi che porta al collasso strutturale.

1.3.2.3.1

Superfici limite
1) Superficie limite nello spazio delle tensioni: i punti sulla superficie limite sono
critici, quelli all’interno sono ammissibili e quelli all’esterno sono non ammissibili.

Figura 1.44

2) Superficie limite nello spazio delle caratteristiche delle sollecitazioni: sono presenti
sia la superficie elastica sia quella plastica.

Figua 1.45

3) Superficie limite nello spazio delle azioni esterne: la distanza tra l’origine e un
punto al suo interno è il moltiplicatore di collasso λ, mentre la distanza tra tale
punto e la frontiera è il coefficiente di sicurezza K = n * λ Tale superficie limite è di
difficile determinazione perché può variare in relazione a numerosi fattori quali i
carichi applicati, le caratteristiche del materiale e la disposizione dei vincoli.

Figura 1.46

4) Le superfici sono assunte convesse per definizione e ne deriva che:
• data una combinazione di carico ammissibile, il moltiplicatore λcrit sarà il
massimo tra quelli che a partire da questa producono combinazioni ancora
ammissibili;
• data una combinazione di carico ammissibile, il moltiplicatore λcrit è unico;
5) Se le superfici fossero state concave, per un unico situazione si sarebbero potuti
avere stati di tensione critici e stati di tensione ammissibili.

Roma, LUGLIO 2013

Pagina 23


A.A. 2012/2013

ߣଵ = ሬሬሬሬሬറ
‫ܥܣ‬
ሬሬሬሬሬറ ܵ‫݅ܿ݅ݐ݅ݎܿ ݅ݐܽݐ‬
൞ߣଶ = ‫ܦܣ‬
ሬሬሬሬሬറ
ߣଷ = ‫ܤܣ‬

Figura 1.47

‫ܧܣ‬
ߣସ = ሬሬሬሬሬറ ܵ‫݈ܾ݁݅݅ݏݏ݅݉݉ܽ ݋ݐܽݐ‬

1.3.2.3.2

Teoremi dell'analisi limite
1) I teoremi validi dell'analisi limite sono:
• Teorema statico: λcrit è il massimo tra quelli staticamente ammissibili.
• Teorema cinematico: λcrit è il minimo tra quelli cinematicamente compatibili.
• Teorema di unicità: λcrit è l’unico che staticamente ammissibile e
cinematicamente compatibile.
2) Segue un esempio applicativo le cui ipotesi di base sono:
• Le sezioni ruotano rimanendo piane
• Gli spostamenti sono piccoli
• Il legame costitutivo è elasto-plastico perfetto
• La duttilità di elemento o di struttura viene assunta infinita.
• I carichi aumentano rimanendo costante il loro rapporto

1.3.2.3.2.1

Teorema statico
1) In riferimento allo schema seguente:

Figura 1.48

2) Per il sistema S’ cui sono applicate le forze esterne si ha:
ܴ′ଵ = ܴ′ଶ = ܲ

‫′ܯ‬஺ = ܲ ∗ ܽ = ܴ′ଵ ∗ ܽ

‫′ܯ‬஻ = ܴ′ଵ ∗ ሺܽ + ܾሻ − ܲ ∗ ܾ

Roma, LUGLIO 2013

Pagina 24


A.A. 2012/2013

3) Per il sistema S’’ associato all’incognita iperstatica si ha:
߯
݈
߯
ܴ′′ଶ = −
݈
߯
‫′′ܯ‬஺ = ܴ′′ଵ ∗ ܽ = ∗ ܽ
݈
ܴ′′ଵ =

‫′′ܯ‬஻ = ܴ′′ଵ ∗ ሺܽ + ܾሻ =

߯
∗ ሺܽ + ܾሻ
݈

‫′′ܯ‬஼ = ܴ′′ଵ ∗ ሺܽ + ܾ + ܽሻ =

߯
∗݈ =߯
݈

4) Sommando i diagrammi dei momenti di S’ e di S’’ si ha:

߯
‫ܯ‬஺ = ‫′ܯ‬஺ − ‫′′ܯ‬஺ = ቀܲ − ቁ ∗ ܽ
݈

‫ܯ‬஻ = ‫′ܯ‬஻ − ‫′′ܯ‬஻ = ܲ ∗ ܽ −
‫ܯ‬஼ = ‫′′ܯ‬஼ = ߯

߯
∗ ሺܽ + ܾሻ
݈

5) Negli stati staticamente ammissibili si ha equilibrio e non collasso, per cui vanno
imposte le condizioni di ammissibilità:
߯
‫ܯ‬஺ ≤ ‫ܯ‬௉ → ቀܲ − ቁ ∗ ܽ ≤ ‫ܯ‬௉
‫ۓ‬
݈
ۖ
߯
‫ܯ۔‬஻ ≤ ‫ܯ‬௉ → ܲ ∗ ܽ − ݈ ∗ ሺܽ + ܾሻ ≤ ‫ܯ‬௉
ۖ
‫ܯ‬஼ ≤ ‫ܯ‬௉ → ߯ ≤ ‫ܯ‬௉
‫ە‬

6) Il sistema è una volta iperstatico, quindi per arrivare alla formazione di un
meccanismo servono due cerniere plastiche, che si ricavano imponendo le
precedenti condizioni di ammissibilità due a due; le possibili combinazioni delle
condizioni critiche sono:
•

1+3

•

2+3

൝

߯
‫ܯ‬௉ ‫ܯ‬௉
ܽ+݈
ቀܲ௖௥ − ቁ ∗ ܽ = ‫ܯ‬௉
→ ܲ௖௥ =
+
→ ܲ௖௥ = ‫ܯ‬௉ ∗
݈
ܽ
݈
ܽ∗݈
߯ = ‫ܯ‬௉

߯
‫ܯ‬௉ ‫ܯ‬௉
ܾ
ܽ+ܾ+݈
ܲ௖௥ ∗ ܽ − ∗ ሺܽ + ܾሻ = ‫ܯ‬௉
൝
+
∗ ൬1 + ൰ → ܲ௖௥ = ‫ܯ‬௉ ∗
→ ܲ௖௥ =
݈
ܽ
ܽ∗݈
ܽ
݈
߯ = ‫ܯ‬௉

Nonostante il valore massimo sia quello dalla seconda combinazione, quello esatto
è quello dalla prima in quanto è l'unico cinematicamente compatibile in quanto
nella seconda combinazione si ha un momento in A maggiore di quello plastico
massimo ammissimibile.

Roma, LUGLIO 2013

Pagina 25


A.A. 2012/2013

1.3.2.3.2.2
1.3.2.3.2.2.1

Teorema cinematico
Trave iperstatica
1) E' necessario individuare i cinematismi di collasso compatibili con i vincoli quindi lil
posizionamento delle cerniere plastiche nelle zone di vincolo o nei punti di
applicazione delle cerniere plastiche. In riferimento allo schema statico
precedente, si necessita la formazione di due cerniere:

Figura 1.49
ߜ′஻ = ߜ′஺ ∗
௔ା௕

ߠ′஺ = ߜ′஺ ∗ ቀ௔ + ௔ା௕ቁ

௔

ଵ

ଵ

‫ܮ‬௘௦௧ = ‫ܮ‬௜௡௧

ಲ
ߠ′஼ = ௔ା௕

ఋᇱ

ܲ௖௥ଵ ∗ ߜ′஺ + ܲ௖௥ଵ ∗ ߜ′஻ = ‫ܯ‬௉ ∗ ߠ′஺ + ‫ܯ‬௣ ∗ ߠ′஼

ܽ
1
1
ߜ′஺
= ‫ܯ‬௉ ∗ ߜ′஺ ∗ ൬ +
൰ + ‫ܯ‬௣ ∗
ܽ+ܾ
ܽ+ܾ
ܽ ܽ+ܾ
ܽ
1
2
ቁ = ‫ܯ‬௉ ∗ ൬ +
൰
ܲ௖௥ଵ ∗ ቀ1 +
ܽ+ܾ
ܽ ܽ+ܾ
݈
ܽ+݈
ܲ௖௥ଵ ∗ ൬
൰ = ‫ܯ‬௉ ∗ ൬
൰
ܽ+ܾ
ܽ ∗ ሺܽ + ܾሻ
ܽ+݈
ܲ௖௥ଵ = ‫ܯ‬௉ ∗ ൬
൰
ܽ∗݈
ܲ௖௥ଵ ∗ ߜ′஺ + ܲ௖௥ଵ ∗ ߜ′஺ ∗

Figura 1.50

ߜ′′஺ = ߜ′′஻ ∗ ௔ା௕
௔

ߠ′′஻ = ߜ′′஻ ∗ ቀ௔ + ௔ା௕ቁ
ଵ

ଵ

‫ܮ‬௘௦௧ = ‫ܮ‬௜௡௧

ߠ′′஼ =

ఋᇱᇱಳ
௔

ܲ௖௥ଶ ∗ ߜ′′஻ + ܲ௖௥ଶ ∗ ߜ′′஺ = ‫ܯ‬௉ ∗ ߠ′′஻ + ‫ܯ‬௣ ∗ ߠ′′஼
ܽ
1
1
ߜ′′஻
ܲ௖௥ଶ ∗ ߜ′′஺ + ܲ௖௥ଶ ∗ ߜ′′஺ ∗
= ‫ܯ‬௉ ∗ ߜ′′஻ ∗ ൬ +
൰ + ‫ܯ‬௣ ∗
ܽ
ܽ+ܾ
ܽ ܽ+ܾ
ܽ
2
1
ቁ = ‫ܯ‬௉ ∗ ൬ +
൰
ܲ௖௥ଶ ∗ ቀ1 +
ܽ+ܾ
ܽ ܽ+ܾ
݈
ܽ+ܾ+݈
ܲ௖௥ଶ ∗ ൬
൰ = ‫ܯ‬௉ ∗ ൬
൰
ܽ+ܾ
ܽ ∗ ሺܽ + ܾሻ
ܽ+ܾ+݈
ܲ௖௥ଶ = ‫ܯ‬௉ ∗
ܽ∗݈
2) Tra i due valori devo scegliere il minore che sarà quello esatto:
ܲ௖௥ଶ > ܲ௖௥ଵ

Tale valore coincide con quello trovato con il th. statico.
Roma, LUGLIO 2013

Pagina 26


A.A. 2012/2013

1.2.3.2.2.2.2

Telaio iperstatico
1) Si applica la stessa procedura precedente ad un telaio una volta iperstatico per il
quale si necessita la formazione di due cerniere plastiche con conseguenti 6
possibili cinematismi:

Figura 1.51

‫ ∗ ߠ ∗ ܪ‬ℎ = ‫ܯ‬௉஼ ∗ ߠ + ‫ܯ‬௉஽ ∗ ߠ

− ‫ ∗ ߠ ∗ ܪ‬ℎ = ‫ܯ‬௉஼ ∗ ߠ + ‫ܯ‬௉஽ ∗ ߠ
1
‫ ∗ ߠ ∗ ܪ‬ℎ + ∗ ܸ ∗ ݈ ∗ ߠ = ‫ܯ‬௉ா ∗ 2 ∗ ߠ + ‫ܯ‬௉஽ ∗ 2 ∗ ߠ
2
1
− ‫ ∗ ߠ ∗ ܪ‬ℎ + ∗ ܸ ∗ ݈ ∗ ߠ = ‫ܯ‬௉ா ∗ 2 ∗ ߠ + ‫ܯ‬௉஽ ∗ 2 ∗ ߠ
2
1
‫ ∗ ߠ ∗ ܪ‬ℎ + ∗ ܸ ∗ ݈ ∗ ߠ = ‫ܯ‬௉஼ ∗ 2 ∗ ߠ + ‫ܯ‬௉ா ∗ 2 ∗ ߠ
2
1
− ‫ ∗ ߠ ∗ ܪ‬ℎ + ∗ ܸ ∗ ݈ ∗ ߠ = ‫ܯ‬௉஼ ∗ 2 ∗ ߠ + ‫ܯ‬௉ா ∗ 2 ∗ ߠ
2

2)
Dai sei precedenti meccanismi di collasso si generano delle rette, la loro
intersezione crea la superficie limite di collasso di questa struttura, da cui è possibile
determinare il moltiplicatore di collasso ߣ =

ை௉ ∗
ை௉

Figura 1.52

Roma, LUGLIO 2013

Pagina 27

A.A. 2012/2013

1.4.
1.4.1


Aspetti particolari dell'analisi plastica
Comportamento ciclico della sezione inflessa
1) Si consideri una sezione semplicemente inflessa fino alla plasticizzazione delle fibre
più tese:

Figura 1.53

2) A partire da tale condizione, si considerino tre possibili situazioni:
• scarico

Figura 1.54

•

inversione del carico

•

inversione con sfruttamento delle risorse plastiche

Figura 1.55

Figura 1.56

3) E' evidente che nel comportamento ciclico la sezione tende a diminuire la propria
rigidezza in maniera crescente con l'aumentare dei cicli e il conseguente
sfruttamento sempre maggiore delle risorse plastiche.

Roma, LUGLIO 2013

Pagina 28

A.A. 2012/2013

1.4.2


Influenza del taglio sul comportamento elastoplastico a flessione
1) Essendo l'influenza del taglio un aspetto di difficile trattazione, si fa riferimento al
criterio di Von Mises:
‫߬ → 0 = ߪ ݁ݏ‬௬ = 0.517 ∗ ߪ௬
ߪ ଶ + 3 ∗ ߬ ଶ = ߪ௬ ଶ → ൜
‫ߪ = ߪ → 0 = ߬ ݁ݏ‬௬
2) Si ricorda che il taglio varia in maniera parabolica su una sezione elastica.
3) Si suppone che non ci sia taglio nella parte delle fibre plasticizzate, per cui nel
grafico complessivo dato dalla somma delle σ e delle τ si nota una parte dove c’è la
rottura per flessione e una parte dove c’è la rottura per taglio.

Figura 1.57

Figura 1.58

Figura 1.59

4) Il taglio riduce la resistenza a flessione; al diagramma della sezione tutta
plasticizzata sottraggo la riduzione di resistenza a flessione ΔM.

1.4.3

Interazione tra instabilità e plasticità
1) Si considera l'instabilità attraverso la formulazione continua

Figura 1.60

2) Con l’ipotesi dei piccoli spostamenti si scrive:
1
߯ = ≅ ‫ ݕ‬ᇱᇱ → ‫ܯ‬௜௡௧ = −‫′′ݕܫܧ‬
ܴ
Roma, LUGLIO 2013

Pagina 29


A.A. 2012/2013

Scrivo l’equazione di equilibrio interno dei momenti:
ܲ
‫ ݕ‬ᇱᇱ + ∗ ‫0 = ݕ‬
‫ܫܧ‬
La soluzione è della forma:
ቄ

‫ݕ‬ሺ‫ݔ‬ሻ = ‫ ∗ ܣ‬sin ߙ‫ ∗ ܤ + ݔ‬cos ߙ‫ ݔ‬

‫ ∗ ܣ‬sin ߙ‫ܮ‬଴ = 0
→
‫0=ܤ‬

ߙ‫ܮ‬଴ = ݊ ∗ ߨ →

ߙ=

௡∗గ
௅బ

‫ݕ‬ሺ‫ݔ‬ሻ = ‫ ∗ ܣ‬sin ቀ ௅ ‫ݔ‬ቁ
௡∗గ

Figura 1.61

బ

3) Sostituendo la soluzione trovata nell'equazione di equilibrio si determina il carico
critico:
݊∗ߨ
݊ ∗ ߨ ଶ
݊∗ߨ
݊∗ߨ
‫ ݕ‬ᇱ ሺ‫ݔ‬ሻ = ‫∗ ܣ‬
∗ cos ൬
∗ ‫ݔ‬൰ ‫ ݕ‬ᇱᇱ ሺ‫ݔ‬ሻ = −‫ ∗ ܣ‬൬
൰ ∗ sin ൬
∗ ‫ݔ‬൰
‫ܮ‬଴
‫ܮ‬଴
‫ܮ‬଴
‫ܮ‬଴
−‫ ∗ ܣ‬൬

݊∗ߨ
ܲ
݊∗ߨ
݊∗ߨ ଶ
൰ ∗ sin ൬
∗ ‫ݔ‬൰ + ∗ ‫ ∗ ܣ‬sin ൬
∗ ‫ݔ‬൰ = 0
‫ܮ‬଴
‫ܫܧ‬
‫ܮ‬଴
‫ܮ‬଴
−൬

݊∗ߨ ଶ ܲ
݊∗ߨ ଶ
൰ +
= 0 → ܲ௖௥ = ‫ ∗ ܫܧ‬൬
൰
‫ܮ‬଴
‫ܫܧ‬
‫ܮ‬଴

4) Ora posso scrivere la formula di σcr in funzione della snellezza:
ܲ௖௥ =

ܲ௖௥ ‫ܫܧ‬
ߨ ଶ
=
∗൬ ൰
‫ܣ‬
‫ܣ‬
‫ܮ‬଴

5) Introducendo le definizioni di raggio di inerzia e snellezza:

‫ܫ‬
‫ߩ ۓ‬ଶ =
࣊૛
‫ܣ‬
→ ࣌ࢉ࢘ = ࡱ ∗ ૛
ࣅ
‫ܮ = ߣ ۔‬଴
‫ە‬
ߩ

6) A questo punto sono possibili due situazioni:
•

Legame elastoplastico perfetto:esiste una snellezza critica
‫ߨ ∗ ܧ‬ଶ
‫ܧ‬
= ߪ௬ → ߣ∗ = ߨ ∗ ඨ
∗ଶ
ߪ௬
ߣ

Roma, LUGLIO 2013

Pagina 30

A.A. 2012/2013


Figura 1.62

•

Legame elasto plastico perfetto:esiste una snellezza legata alla tensione di
snervamento e una legata a quella ultima:
‫ܧ‬௧ ∗ ‫ ݕ ∗ ܫ‬ᇱᇱ + ܲ ∗ ‫′ܲ → 0 = ݕ‬௖௥ =

Figura 1.63

ߨ ଶ ∗ ‫ܧ‬௧ ∗ ‫ܫ‬
‫ܮ‬଴

7) Il modulo elastico tangente è una rappresentazione delle medie di tutte le E delle
fibre, per cui è compreso tra il modulo elastico e il modulo elasto - plastico; non
sono state introdotte le imperfezioni perché vengono inserite come una
deformazione iniziale.

Roma, LUGLIO 2013

Pagina 31

A.A. 2012/2013

SEZIONE 2

STABILITA' DELL'EQUILIBRIO

2.1


Aspetti generali
1) Nell'ambito della progettazione di un'opera di ingegneria, oltre a tener conto della
resistenza che un dato elemento strutturale è in grado di offrire, è fondamentale
anche tenere conto della possibilità che esso presenti una instabilità
dell'equilibrio, intendendo quest'ultimo come un mutamento sostanziale dei
caratteri della sua deformazione.
2) Dato un elemento in una configurazione di equilibrio sottoposto a carichi via via
crescenti, può accadere che oltre un certo limite l'equilibrio da essere stabile
diventa instabile, e cioè diventa tale che ad una variazione infinitesima qualsiasi
della sua configurazione non corrisponde il ristabilimento della configurazione
originaria. In pratica, in una situazione di equilibrio instabile lo spostamento
infinitesimo prodotto da una ipotetica causa esterna fa sì che il corpo cambi
completamente la sua configurazione, tendendo a raggiungere un altro stato di
equilibrio (stavolta stabile) sotto quello stesso carico, che in alcuni casi è
effettivamente possibile.
3) Le ipotesi alla base della trattazione sono:
•
spostamenti piccoli o grandi
•
equilibrio nella configurazione deformata o indeformata
•
legame elastico
•
forze posizionali

2.2
2.2.1

Studio del comportamento critico e post-critico di un'asta rigida
Condizione di vincolo 1
1) Si consideri la seguente struttura:

Figura 2.1

La struttura è un sistema ad un grado di libertà (la rotazione θ) quindi basta un
solo parametro per descrivere il moto del sistema.
2) L'energia associata al sistema è:
1
1
‫ܧ‬௣௧ = ‫ܧ‬௘௦௧ + ‫ܧ‬௜௡௧ = −ܲ ∗ ‫ݒ‬஻ + ∗ ݇ ∗ ߴ ଶ = −ܲ ∗ ݈ ∗ ሺ1 − cos ߴሻ + ∗ ݇ ∗ ߴ ଶ
2
2

Roma, LUGLIO 2013

Pagina 32


A.A. 2012/2013

2.2.1.1
2.2.1.1.1

Cinematica ed equilibrio
Trattazione completa
1) Si scrive la cinematica in grandi spostamenti:

‫ݑ‬஻ = ݈ ∗ sin ߴ

൜
‫ݒ‬஻ = ݈ ∗ (1 − cos ߴ)

2) L'equilibrio nella configurazione deformata:

ߑ M୅ = 0 → −P ∗ ‫ݑ‬஻ + ݇ ∗ ߴ = 0 → −ܲ ∗ ݈ ∗ sin ߴ + ݇ ∗ ߴ = 0

2.2.1.1.2

ܲ=

Linearizzazione degli spostamenti

݇
ߴ
∗
݈ sin ߴ

1) Si linearizza la cinematica mediante lo sviluppo in serie di Taylor:

݂ ௡ ሺܽሻ
Tሺxሻ = ෍
∗ ሺ‫ܽ − ݔ‬ሻ௡
݊!
∞

‫ ߠ ݈ = ݑ‬

൜ ஻
‫ݒ‬஻ = 0

௡ୀ଴


ߑ M୅ = 0 → −P ∗ ‫ݑ‬஻ + ݇ ∗ ߴ = 0 → −ܲ ∗ ݈ ∗ ϑ +݇ ∗ ߴ = 0

2.2.1.1.3

ܲ=

݇
݈

Equilibrio nella configurazione indeformata
1) La cinematica è linearizzata:

‫ ߠ ݈ = ݑ‬

൜ ஻
‫ݒ‬஻ = 0

2) L'equilibrio nella configurazione indeformata:

ߑ M୅ = 0 → −P ∗ ‫ݑ‬஻ + ݇ ∗ ߴ = 0 → −P ∗ 0 + ݇ ∗ ϑ = 0
ϑ=0

2.2.1.1.4

Conclusioni
1) Si riportano i risultati e il riassunto delle ipotesi utilizzate:

Figura 2.2

Caso
I
II
III

Roma, LUGLIO 2013

Ipotesi cinematica
Grandi spostamenti
Piccoli spostamenti
Piccoli spostamenti

Ipotesi di equilibrio
Configurazione deformata
Configurazione deformata
Configurazione indeformata

Teoria
Del primo ordine
Del secondo ordine

Pagina 33


A.A. 2012/2013

2.2.1.2
2.2.1.2.1

Approccio energetico

‫ݑ‬஻ = ݈ ∗ sin ߴ

൜
‫ݒ‬஻ = ݈ ∗ (1 − cos ߴ)

߲‫ܧ‬௣௧
= −ܲ ∗ ݈ ∗ sin ߴ + ݇ ∗ ߴ = 0
߲ߴ
ߴ
݇
ܲ= ∗
݈ sin ߴ

2) Dal nullo della derivata dell'energia potenziale:

2.2.1.2.2


ஶ

Tሺxሻ = ෍

݂ ௡ ሺܽሻ
∗ ሺ‫ܽ − ݔ‬ሻ௡
݊!

‫ ߠ ݈ = ݑ‬

൜ ஻
‫ݒ‬஻ = 0

௡ୀ଴

2) Dal nullo della derivata dell'energia potenziale:

1
1
1
1
‫ܧ‬௣௧ = −ܲ ∗ ݈ ∗ ൬1 − 1 + ߴ ଶ ൰ + ∗ ݇ ∗ ߴ ଶ = ∗ ܲ ∗ ݈ ∗ ߴ ଶ + ∗ ݇ ∗ ߴ ଶ
2
2
2
2

2.2.1.2.3

߲‫ܧ‬௣௧
= −ܲ ∗ ݈ ∗ ϑ +݇ ∗ ߴ = 0
߲ߴ
݇
ܲ=
݈

Equilibrio nella configurazione indeformata
1) La cinematica è linearizzata:

‫ ߠ ݈ = ݑ‬

൜ ஻
‫ݒ‬஻ = 0

2) L'equilibrio nella configurazione indeformata:

1
1
‫ܧ‬௣௧ = −ܲ ∗ ݈ ∗ ሺ1 − cos ߴሻ + ∗ ݇ ∗ ߴ ଶ = ∗ ݇ ∗ ߴ ଶ = 0
2
2
ϑ=0

2.2.1.2.4

Conclusioni
2) Si riporta il riassunto delle ipotesi utilizzate:
Caso Ordine serie Taylor
I
II

2

III

Roma, LUGLIO 2013

0

1

߲‫ܧ‬௣௧
= −ܲ ∗ ݈ ∗ sin ߴ + ݇ ∗ ߴ
߲ߴ
߲‫ܧ‬௣௧
= −ܲ ∗ ݈ ∗ ϑ +݇ ∗ ߴ
߲ߴ
1
‫ܧ‬௣௧ = ∗ ݇ ∗ ߴ ଶ
2
Equazione

Sviluppo in serie
cosϑ
cosϑ

1
1 − ∗ ߴଶ
2
1

Pagina 34


A.A. 2012/2013

2.2.2


Figura 2.3

2.2.2.1
2.2.2.1.1


‫ݑ‬஻ = ݈ ∗ sin ߴ

൜
‫ݒ‬஻ = ݈ ∗ (1 − cos ߴ)

ߑ M୅ = 0 → −P ∗ ‫ݑ‬஻ + ݇ ∗ ‫ݑ‬஻ ∗ ݈ ∗ cos ߴ = 0
ܲ ∗ ݈ ∗ sin ߴ +݇ ∗ ݈ ଶ ∗ sin ߴ ∗ cos ߴ = 0

ቄ

sin ߴ ∗ (−ܲ ∗ ݈ + ݇ ∗ ݈ ଶ ∗ cos ߴ) = 0

sin ߴ = 0
sin ߴ = 0
→ ቄ
ଶ
−ܲ ∗ ݈ + ݇ ∗ ݈ ∗ cos ߴ = 0
−ܲ + ݇ ∗ ݈ ∗ cos ߴ = 0
ߴ=0
→ ቊcos ߴ = ௉

௞∗௟

ߴ=0
→ ቊϑ = arc cos ቀ ௉

௞∗௟

ቁ

‫ ݈ ∗ ݇ + ݈ ∗ ܲ− → 0 = ߴ ݎ݁݌‬ଶ ∗ cos ߴ = 0
→ ܲ = ݇ ∗ ݈

‫ ݈ ∗ ݇ + ݈ ∗ ܲ− → 0 ≠ ߴ ݎ݁݌‬ଶ ∗ cos ߴ = 0 → ܲ = ݇ ∗ ݈ ∗ cos ߴ

Considerando un imperfezione iniziale θ0, si ottiene il seguente grafico:

Figura 2.4

Roma, LUGLIO 2013

Pagina 35


A.A. 2012/2013

2.2.2.1.2


݂ ௡ ሺܽሻ
Tሺxሻ = ෍
∗ ሺ‫ܽ − ݔ‬ሻ௡
݊!
∞

‫ ߠ ݈ = ݑ‬

൜ ஻
‫ݒ‬஻ = 0

௡ୀ଴

cos ߴ ≅ 1 − ଶ ∗ ߴ ଶ
ଵ

;

sin ߴ ≅ 0

ߑ M୅ = 0 → −P ∗ l ∗ ϑ + ݇ ∗ ݈ ଶ ∗ ߴ = 0 → ܲ = ݇ ∗ ݈ , ∀ߴ

Figura 2.5

2.2.3

3) Lo sviluppo di Taylor fino al 2° ordine viene fatto solo quando si analizza l’energia
potenziale, quando invece si considera l’equilibrio dei momenti gli spostamenti
sono linearizzati, per cui:
cos ߴ ≅ 0 , ‫ߴ ≅ ߴ݊ܽݐ , ߴ ≅ ߴ݊݅ݏ‬



Figura 2.6

2.2.3.1

1) L'espressione dell'energia potenziale:
‫ܧ‬௣௧ = ݇ ∗ ݈ ଶ ∗ ൛2 ∗ ൣ1 − √1 + sin ߴ൧ + sin ߴൟ − ܲ ∗ ݈ ∗ ሺ1 − cos ߴሻ

߲‫ܧ‬௣௧
= ݇ ∗ ݈ ଶ ∗ ሾሺ1 + sin ߴሻି଴.ହ ∗ cos ߴ + cos ߴሿ − ܲ ∗ ݈ ∗ sin ߴ = 0

߲ߴ
݇ ∗ ݈ ଶ ∗ cos ߴ ∗ ሾ1 + ሺ1 + sin ߴሻି଴.ହ ሿ = ܲ ∗ ݈ ∗ sin ߴ
ܲ =

Roma, LUGLIO 2013

݇ ∗ ݈
∗ ሾ1 + ሺ1 + sin ߴሻି଴.ହ ሿ
tan ߴ

Pagina 36


A.A. 2012/2013

Figura 2.7

2.3
2.3.1.
2.3.1.1.

Studio del comportamento critico e post-critico di un sistema di aste

Figura 2.8

E' un sistema nel quale sforzo normale per ogni asta vale:
∆݈
݈଴ − ݈
ܰ =‫∗ܣ∗ܧ= ߝ∗ܣ∗ܧ‬൬ ൰=‫∗ܣ∗ܧ‬൬
൰
݈଴
݈଴
2) Si ricavano le entità cinematiche:
‫ܪ‬
‫ ∗ ܤ = ܪ‬tan ߴ = ݈଴ ∗ cos ߙ ∗ tan ߴ
݈=
sin ߴ
l = ݈଴ ∗ ቀ

ୡ୭ୱ ఈ∗୲ୟ୬ ణ
ቁ
ୱ୧୬ ణ

∆l = ݈଴ ∗ ቀ1 −

3) Si scrive l'equilibrio verticale:

Figura 2.9

Roma, LUGLIO 2013

ቁ
ୱ୧୬ ణ

∆୪

ε=௟ =1−
బ

ୱ୧୬ ణ

ܲ − 2 ∗ ܰ ∗ sin ߴ = 0

ܲ = 2 ∗ ‫( ∗ ܣ ∗ ܧ‬sin ߴ − cos ߙ ∗ tan ߴ)
cos ߙ
ቁ
ܲ = 2 ∗ ‫ ∗ ܣ ∗ ܧ‬sin ߴ ∗ ቀ1 −
cos ߴ

Pagina 37


A.A. 2012/2013

2.4

Studio del comportamento critico e post-critico di un sistema a due g.d.l.
λ

λ

Figura 2.10

2.4.1.
2.4.1.1.

1) Si scrive l'espressione dell'energia potenziale
‫ܧ‬௣௢௧ = ‫ܧ‬௘௦௧ + ‫ܧ‬௜௡௧
1
1
ଶ
ଶ
‫ܧ‬௜௡௧ = ݇ ߠଵ + ݇ ߠଶ ‫ܧ‬௘௦௧ = −ߣ‫ߠݏ݋ܿ − 1(ܮ‬ଵ ) − ߣ‫ߠ(ݏ݋ܿ − 1(ܮ‬ଵ + ߠଶ )
2
2
1
ܿ‫ ߠ − 1 = ߠݏ݋‬ଶ
2
1
1
1 ଶ ߣ‫ܮ‬ሺ(ߠଵ + ߠଶ ሻଶ
ଶ
ଶ
‫ܧ‬௣௢௧ = ݇ ߠଵ + ݇ ߠଶ − ߣ‫ߠ ܮ‬ଵ −

2
2
2
2
2) Si deriva l'energia potenziale rispetto ai due g.d.l. e si eguaglia a 0:
߲‫ݐ݋݌ܧ‬
= ݇ ߠଵ − ߣ‫2 ܮ‬ሺ ߠଶ + ߠଵ ሻ = 0
߲ߠଵ
߲‫ݐ݋݌ܧ‬
= ݇ ߠଶ − ߣ‫2 ܮ‬ሺ ߠଶ + ߠଵ ሻ = 0
߲ߠଶ

ቄቂ

݇
0

ߠ
0
2ߣ‫ܮߣ ܮ‬
ቃ−ቂ
ቃቅ ∗ ൜ ଵ ൠ = 0
ߠଶ
݇
ߣ‫ܮߣ ܮ‬

Bisogna risolvere un problema di autovalori:
detሺ‫ ீܭ ߣ − ܭ‬ሻ = 0 → ߣଵ , ߣଶ
3) Noti gli autovalori, si inseriscono uno alla volta nel sistema ricavando i due
autovettori corrispondenti che rappresentano la forma della deformata. Il carico
critico sarà il minore dei due autovalori.
4) Si riportano di seguito le due deformate con i corrispondenti valori di carico critico:

Roma, LUGLIO 2013

Pagina 38

A.A. 2012/2013
•

1° deformata critica: Pcr=0.382 k/L

•


2° deformata critica: Pcr=2.618 k/L

Figura 2.11

Figura 2.12

Roma, LUGLIO 2013

Pagina 39

A.A. 2012/2013

SEZIONE 3

CRITERI DI PROGETTAZIONE

3.1


Approccio alla progettazione
1) La progettazione strutturale è un processo iterativo volto ad ottenere il miglior
risultato possibile in termini di rapporto funzionalità-costo.
2) L'approccio alla progettazione può essere di due nature:
• Innovativo: partendo da una piccola base di conoscenze, si estende la propria
conoscenza con ricerche e approfondimenti volte alla realizzazione di un'opera
non convenzionale;
• Evolutivo: basandosi su una solida base di conoscenze e di esperienza, la
progettazione è volta al miglioramento di soluzioni già consolidate;
3) In ogni caso alla base di entrambe le vie è necessaria un'opera preliminare di
reperimento delle informazioni e documentazione specifica dal quale il progettista
non può prescindere.
4) Di pari importanza è anche l'utilizzo di sofware di calcolo adeguati e strumenti di
rappresentazione chiari: i primi affinchè il modello elaborato in fase progettuale
sia una affidabile rappresentazione della realtà mentre i secondi affinchè il
prodotto finale sia fruibile e privo di qualsiasi possibilità di fraintendimento.
5) Si riporta di seguito il processo iterativo di progettazione:

Figua 3.1

Roma, LUGLIO 2013

Pagina 40

A.A. 2012/2013


6) Il risultato finale della progettazione deve garantire tutti i requisiti richiesti dalla
normativa di riferimento sia in termini di funzionalità (condizioni di esercizio) sia in
termini di resistenza (condizioni di collasso) in base alla tipologia strutturale in
esame e alle condizioni a contorno.
7) La progettazione strutturale, ovviamente, è sempre affiancata dall'analisi
economica, dalla quale non si può prescindere in qualsiasi attività ingegneristica,
volta al raggiungimento dei minimi costi compatibili con le esigenze funzionali.
8) Nella seguente trattazione è riportata l'analisi del processo progettuale scomposto
in due fasi macrofasi consequenziali:
• Conceptual design
• Processo di ottimizzazione

3.2

Conceptual Design
1) Il Conceptual Design si colloca nelle prime fasi del processo di progettazione. Le
decisioni prese in questa fase hanno una significativa influenza su fattori come
costi, prestazioni, affidabilità, sicurezza ed in generale sul successo commerciale di
un prodotto. Durante questa fase si operano la maggior parte delle scelte
strategiche, si prendono decisioni importanti che successivamente, solo con
difficoltà, possono essere cambiate. Sebbene una grande quantità di informazioni
siano manipolate in un tempo relativamente ristretto, il Conceptual Design è la
parte della progettazione meno supportata da strumenti dedicati.
2) Il punto di partenza è il riconoscimento delle azioni agenti sulla struttura e la scelta
del funzionamento che si vuole conferire alla stessa per resistere alle stesse in
base alla quale si progetta la disposizione degli elementi e la dimensione delle
sezioni.
3) Il Conceptual Design è dunque un approccio globale alla progettazione che
dipende dalla conoscenza e dalla sensibilità dell'ingegnere che non può essere
inquadrato in uno schema fisso.

3.2.1
3.2.1.1

Performance strutturali richieste
Rigidezza strutturale (SLE)
1) Il requisito fondamentale che ogni struttura deve soddisfare in condizioni di
esercizio è la bassa deformabilità quindi è necessario assegnare ad ogni elemento
strutturale un'adeguata rigidezza e disporli in modo da conferirne alla struttura nel
complesso.
2) Il controllo della rigidezza della struttura avviene mediante l'analisi di:
• frecce (travi e solai)
• drift (globali e locali)
3) Tali parametri tradizionali per il controllo deformativo sono di non facile
valutazione e non troppo affidabili se si pensa al comportamento globale della
struttura quindi il parametro migliore è la frequenza propria della struttura, che
deriva da un'analisi modale dinamica, e che permette di valutare in maniera
sintetica ma complessiva la rigidezza.

Roma, LUGLIO 2013

Pagina 41


A.A. 2012/2013

3.2.1.2

Instabilità (SLE/SLU)
1) La valutazione del carico critico nelle aste compresse è un aspetto che riguarda sia
le condizioni di esercizio sia quelle di collasso in quanto mette in gioco sia la
rigidezza che la capacità ultima dell'elemento.
2) Tale aspetto è evidente già dalla considerazione del caso più semplice di calcolo
del carico critico ovvero l'espressione di Eulero:
ߨ ଶ ‫ܬ ܧ‬
‫ܮ‬ଶ
E' evidente che un aumento del modulo elastico corrisponde ad un aumento della
capacità dell'elemento quindi abbiamo un'interazione tra la rigidezza e la
resistenza dell'elemento.
ܲ௖௥ =

3.2.1.3

Resistenza (SLU)
1) La resistenza ultima della struttura è necessariamente uno degli aspetti
fondamentali da considerare nella progettazione strutturale. Si intende, infatti, la
capacità ultima che deve essere tale da garantire l'integrità sotto le azioni di
progetto in relazione al tempo di ritorno assegnato all'opera.
2) Si sottolinea che nelle costruzioni metalliche la resistenza ultima della struttura è
l'aspetto meno delicato e di più semplice valutazione in quanto l'acciaio è un
materiale di ottime qualità .

3.2.1.4

Duttilità (SLU)
1) Per duttilità della struttura si intende la capacità della stessa. di subire delle
deformazioni plastiche senza giungere al limite del collasso. E' dunque una misura
dell'escursione in campo plastico che la struttura è in grado di sopportare.
2) La valutazione della duttilità è centrale nella progettazione moderna in quanto
l'attuale capacità di valutare l'azione sismica di progetto ha fatto si che in fase di
progetto le azioni da considerare siano tale da rendere economicamente
insostenibile la realizzazione di una struttura che resista solamente in campo
elastico. Accettare l'ingresso in campo plastico della struttura rappresenta l'unica
via per resistere alle azioni esterne e questo pone il problema centrale del delicato
controllo del danneggiamento.
3) La duttilità, come l'instabilità, è un aspetto che rientra anche nelle condizioni di
esercizio in quanto si lavora sulla duttilità: in questo caso, però, un aumento della
rigidezza gioca a sfavore in quanto la struttura diventa più fragile e il
comportamento meno dissipativo.

3.2.2

Scelte progettuali
1) In funzione delle performance strutturali richieste, si procede alle scelte
progettuali volte ad individuare innanzitutto la geometria da assegnare alla alla
struttura.
2) La disposizione degli elementi deve essere studiata in funzione del
comportamento che si vuole loro assegnare in modo che lavorino bene con tutti gli
altri e garantiscano i requisiti in tutti gli aspetti.

Roma, LUGLIO 2013

Pagina 42

A.A. 2012/2013


3) Oltre che al comportamento delle aste particolare attenzione va posta anche al
riconoscimento e allo studio delle zone diffusive e dei nodi che rappresentano per
le strutture metalliche un aspetto caratterizzante della progettazione .

3.2.2.1
3.2.2.1.1

Figua 3.2

3.2.2.1.2

Tipologie elementari
Concentric Braced Frames (CBF)
1) Tale tipologia strutturale è composta di elementi incernierati e sfrutta il principio
della triangolazione degli elementi per mantenere tutti gli sforzi puramente assiali.
2) Offre caratteristiche di ottima rigidezza e questo si traduce nel fatto che le
verifiche allo stato limite di esercizio sono facilmente soddisfatte.
3) Data la bassa duttilità,però, mostrano problemi allo stato limite ultimo, dovuti al
comportamento puramente assiale della struttura che non possiede risorse
plastiche prima di arrivare al collasso.
4) Anche l'instabilità delle aste compresse è un problema rilevante nell'analisi agli
SLU.

Moment Resisting Frames (MRF)
1) Tale tipologia strutturale è composta sostanzialmente da un telaio semplice con
comportamento flessionale
2) Data l'elevata duttilità e capacità portante, le verifiche allo stato limite ultimo sono
facilmente soddisfatte.
3) Considerata.però l'elevata deformabilità, mostrano problemi allo stato limite
d’esercizio,
4) Per questo tipo di struttura si può ottimizzare il comportamento flessionale
dividendola in sottostrutture oppure inserendo degli elementi strutturali come gli
Outrigger che riducono i drift della stessa.

Figua 3.3

Roma, LUGLIO 2013

Pagina 43

A.A. 2012/2013

3.2.2.1.3


Eccentric Braced Frames (EBF)
1) Tale tipologia strutturale presenta un livello intermedio delle risposte rispetto agli
elementi CBF ed MRF perché prende le caratteristiche di rigidezza delle strutture
CBF e quelle di duttilità delle MRF.
2) Caratteristica particolare di questa tipologia strutturale è la presenza degli
elementi link che si occupano di concentrare su di loro le deformazioni plastiche
facendo in modo che la struttura presenti delle capacità dissipative.
3) Si affida quindi agli elementi link il comportamento flessionale duttile e al resto
della struttura il comportamento assiale rigido. Per questo loro comportamento gli
elementi link non rispettano le ipotesi di de Saint Venant e perciò entrano nella
categoria di zone diffusive.

Figua 3.4

3.2.2.2
3.2.2.2.1

Nodi
Distinzione funzionale
1) Si possono distinguere due tipologie di zone con diverso comportamento:
• B-regions: zone in cui vale la Teoria di De Saint Venant e la determinazione di σ e
௅
di ε è semplice. Tale comportamento è valido solo per elementi 25 ≥ ௛ ≥ 5.Gli
elementi che presentano questo comportamento sono colonne, travi e diagonali.
• D-regions: zone, dette diffusive, in cui serve una modellazione bidimensionale o
tridimensionale degli sforzi e la determinazione di σ e di ε è complessa. Il Le Dregions sono individuate da::
- Cambio di geometria, che può essere globale (cambio degli assi) o locali
(cambio delle sezioni),
- Cambio del materiale, per esempio tra calcestruzzo e acciaio, Presenza di
carichi, che possono essere concentrati o distribuiti,
- Presenza di vincoli, e tutti i casi dove non è valida la Teoria di De Saint
Venant.

Figua 3.5

Roma, LUGLIO 2013

Pagina 44

A.A. 2012/2013

3.2.2.2.2


Rigidezze nodali
1) La progettazione del nodo è un punto fondamentale della progettazione di
costruzioni metalliche in quanto la tipologia di vincolo che si vuole riprodurre
influenza la risposta strutturale.

Figua 3.6

2) La riproduzione di un vincolo non è univoca ma dipende dal modo di assemblare
gli elementi di cui si dispone nella realtà, con la certezza che è impossibile
riprodurre concretamente un vincolo perfetto.

Figua 3.7

3) Nella realtà dei calcoli il modo giusto di approcciare al problema è quello di
considerare sempre una presenza oppure una perdita di rigidezza rispetto ai casi
ideali, questo per considerare situazioni intermedie da quelle ideali che nella
realtà non si presentano mai.

Figua 3.8

Roma, LUGLIO 2013

Pagina 45

A.A. 2012/2013


4) Il processo logico che si può adottare è che in presenza di un vincolo si ipotizza che
gli spostamenti vincolati possiedano una rigidezza tendente al infinito invece per
gli spostamenti liberi che la rigidezza tenda a zero ( il che si traduce in una
resistenza residua).

Figua 3.9

5) A titolo di esempio,si considera una cerniera vincolata a terra nella quale arriva
una trave IPE.

Figua 3.10

6) La riproduzione di una cerniera per elementi metallici viene fatta grazie alle
bullonature, ma la disposizione dei bulloni può generare un braccio tra gli stessi
con la conseguenza che si possono generare dei momenti resistenti,
allontanandosi dalla cerniera ideale.
7) Si vuole evitare la formazione di questi momenti imponendo un braccio nullo tra i
bulloni, nonostante inevitabilmente saranno le deformazioni che si generano nei
bulloni a creare questi momenti residui che in ogni caso saranno molto più piccoli.
Ne deriva che le rigidezze nodali possono tendere a zero (infinito) però non
potranno essere uguali a zero (infinito).
8) Qundi in presenza di un nodo conviene sempre considerare le imperfezioni dei
vincoli introducendo delle molle, siano esse rotazionali o estensionali, in funzione
delle sollecitazioni cui è sottoposta la struttura. In tutti e due i casi il valore della
rigidezza (K) può variare da zero a infinito, questo per la sua dipendenza dalla
perfezione che si vuole ottenere nella realizzazione del vincolo.

Figua 3.11

Roma, LUGLIO 2013

Pagina 46

A.A. 2012/2013


Figua 3.12
‫߮∗ܭ= ܯ‬

‫߂∗ߣ= ܨ‬

9) Si riporta un diagramma di classificazione dei nodi in base alle seguenti grandezze
adimensionali:
‫ܭ‬௜ ∗ ‫ܮ‬
ഥ
‫=ܭ ۓ‬
‫ܫ ∗ ܧ‬௕
ۖ
ۖ
‫ܯ‬௨
ഥ
‫=ܯ‬
‫ܯ‬௣௕
‫۔‬
ۖ
ۖ߮ = ߮ ∗ ‫ܫ ∗ ܧ‬௕
ത
‫ܯ‬௣௕ ∗ ‫ܮ‬
‫ە‬

Figua 3.13

Roma, LUGLIO 2013

Pagina 47


A.A. 2012/2013

3.3

Ottimizzazione
1) Per ottimizzazione strutturale si intende il processo di determinazione della
geometria della struttura che garantisca la migliore resistenza e rigidezza nei
confronti delle azioni esterne con costi più contenuti possibili.
2) E' un processo iterativo che riguarda tutti gli aspetti funzionali della struttura il cui
numero di tentativi dipende dal livello di dettaglio e quindi dal grado di
affinamento che si vuole raggiungere.
3) Definita l'idea strutturale base, quindi, si parte da una geometria di primo
tentativo, molto spesso basata sull'esperienza di opere esistenti simili, e si procede
con l'ottimizzazione modificando geometria e sezioni fino al raggiungimento del
minimo nell'analisi dei costi.

Analisi dei costi

Figura 3.14

Costo zone
diffusive
Costo

Costo zone
Bernoulli
Costo totale

MIN Ctot

n

4) Il processo di ottimizzazione può essere scomposti in due fasi:
1. Analisi: si individuano i dati della struttura (geometria,materiali, condizioni
a contorno) e si elaborano per ottenere dei risultati da sottoporre a
verifica.
2. Progettazione: se la verifica non è soddisfatta si procede alla modifica dei
dati di partenza e si ripete la fase di calcolo e le verifiche.
5) Nella progettazione delle costruzioni metalliche, il processo di ottimizzazione è
fondamentale in quanto l'acciaio è un materiale costoso quindi una riduzione del
peso significa un risparmio economico immediato e non indifferente.
6) Distinguiamo due macroprocessi di ottimizzazione:
• Ottimizzazione per livelli: si interviene in maniera graduata nella variazione
dei singoli elementi fino ad introdurne di nuovi se necessario
• Ottimizzazione per risposta: si interviene sul singolo elemento in funzione del
tipo di sollecitazione cui è sottoposto in modo che il suo comportamento sia
ottimale.

3.3.1
3.3.1.1

Ottimizzazione per livelli
Sizing
1) Per sizing si intende il processo volto al dimensionamento della sezione
dell'elemento ottima quindi alla scelta della sezione commerciale più piccola che
soddisfi il limite tensionale imposto in fase di progetto.

Roma, LUGLIO 2013

Pagina 48

A.A. 2012/2013


2) L'obiettivo del sizing è la situazione di fully stressed optimization cioè la condizione
in cui tutta la struttura al massimo delle proprie capacità sfruttando al massimo
tutta la propria resistenza.
3) E' evidente che risulta impossibile giungere ad un livello in cui tutti gli elementi
sono sottoposti allo stesso tasso di lavoro quindi la soluzione deve tendere alla
migliore ideale senza però dimenticare di affiancare l'analisi limite tensionale con
quella di deformabilità (una sezione più piccola lavora ad un tasso più elevato ma è
anche molto meno rigida).

Figura 3.15

3.3.1.2

Morfologica
1) Per ottimizzazione morfologica si intende un processo complesso volto alla ricerca
della forma ottimale da assegnare all'elemento strutturale in funzione dello stato
di tensione interno cui sarà sollecitato
2) Si tratta di un processo evolutivo in cui, partendo da una geometria semplice
caratterizzata da massa distribuita uniformemente, si giunge ad una ridistribuzione
ottimale delle masse stesse secondo la disposizione che meglio asseconda il
probabile flusso tensionale cui l'elemento sarà sottoposto durante la sua vita utile.
3) Data la complessità dell'approccio, tale processo di ottimizzazione può essere
realizzato solo mediante l'utilizzo di software specifici.

3.3.1.3

Topologica
1) Per ottimizzazione topologica si intende il processo di modifica della disposizione e
inserimento/eliminazione di elementi volto a generare un percorso di scarico delle
azioni esterne quanto più favorevole possibile.
2) Rispetto al sizing, dunque, è un processo più evoluto in quanto non c'è solo una
variazione delle sezioni ma necessita di individuare a priori il percorso di carico che
si vuole sviluppare all'interno della struttura ed assecondarlo con la disposizione
degli elementi.
3) L'ottimizzazione topologica risente, quindi, molto maggiormente della sensibilità
del progettista e dalla sua capacità di individuare il percorso di carico più breve che
è sempre l'ottimo progettuale.

Roma, LUGLIO 2013

Pagina 49

A.A. 2012/2013


Figura 3.16

3.3.1.4

Introduzione di una sottostruttura
1) L'introduzione di una sottostruttura all'interno del modello strutturale rientra nel
processo di ottimizzazione per livelli come soluzione finale.
2) Si tratta di inserire un blocco funzionale in grado di modificare il comportamento
globale della struttura grazie alle proprie caratteristiche ed adeguarlo alle esigenze
funzionali richieste

3.3.1.4.1

Uso dell'Outrigger
1) L'Outrigger fu ideato dall'ingegnere indiano Khan Fazlur e consiste in una
controventatura in direzione orizzontale situata tutta sullo stesso livello.
2) Rispetto ai controventi verticali tradizionali, gli outriggers trasformano gli sforzi
taglianti, che nascono in seguito alle azioni orizzontali, in sforzi assiali in modo da
ridurre gli spostamenti di piano assoluti e relativi.

Figua 3.17

Roma, LUGLIO 2013

Pagina 50

A.A. 2012/2013


3) Per la scelta del numero degli outrigger e del loro posizionamento all’interno di
una struttura è necessario effettuare uno studio nel quale si possano notare i vari
effetti delle combinazioni di posizione e di numero. Questo fattore si nota bene
nello studio dei drift: inserendo un outrigger si nota che i drift vengono ridotti fino
a un terzo rispetto alla configurazione che ne è priva.

Figura 3.18

4) Si possono inserire più livelli di outriggers ma in questo caso è necessaria un'analisi
più accurata in quanto è probabile che il costo di realizzazione sia maggiore del
conseguente beneficio funzionale.

Figura 3.19

3.3.2
3.3.2.1
3.3.2.1.1
3.3.2.1.1.1

Ottimizzazione per risposta
Assiale
Prinicipi cardine
Trazione
1) Il comportamento degli elementi destinati ad essere sollecitati a trazione deve
essere migliorato aumentandone la robustezza, ovvero la capacità di subire danni
locali senza giungere al collasso.

Roma, LUGLIO 2013

Pagina 51


A.A. 2012/2013

2) Questo significa che da un punto di vista funzionale è più conveniente suddividere
l'area dell'elemento realizzandone più di uno, piuttosto che aumentarla. Tale
approccio rispetta il principio cardine valido in ogni applicazione ingegneristica di
"suddivisione della trazione".

Figura 3.20

3.3.2.1.1.2

Compressione
1) Il comportamento degli elementi destinati ad essere sollecitati a compressione
deve essere migliorato aumentandone la portanza critica, ovvero il carico che
porta all'instabilità.
2) Questo significa che da un punto di vista funzionale, al contrario di quanto accade
per gli elementi tesi, conviene adottare sezioni più larghe piuttosto che utilizzare
una serie di elementi più snelli.

Figura 3.21

ܲଵ௖௥ =

3.3.2.1.2
3.3.2.1.2.1

ߨ ଶ ‫ܽ72 ܧ‬ସ
3ߨ ଶ ‫ܽ ܧ‬ସ
∗
> ܲଶ௖௥ =
∗
12
‫ܮ‬௢ ଶ
‫ܮ‬଴ ଶ 12

Aspetti tecnologici
Buckling Restrained Braced Frame (BRBF)
1) Il BRBF è un elemento strutturale in grado di fornire resistenza laterale
impedendo l’instabilità, a sezione stratificata, composto al centro da una sezione
di acciaio coperta da una membrana che non genera attrito, a sua volta rivestita
prima da una sezione di calcestruzzo e poi da una sezione tubolare in acciaio.
2) Questo elemento permette di affidare la trazione alla sezione interna di acciaio e
di affidare la compressione alla sezione esterna di acciaio e calcestruzzo. La
membrana serve a dividere i due comportamenti in modo che non influenzino le
dissipazioni e le rigidezze della struttura.

Roma, LUGLIO 2013

Pagina 52

A.A. 2012/2013


Figura 3.22

3.3.2.1.2.2

Trussed tube
1) Lo sfruttamento del comportamento assiale degli elementi diagonali può essere
utilizzato per ridurre la deformabilità della struttura quindi l'entità degli
spostamenti assoluti e relativi.
2) Tale obiettivo può essere raggiunto passando da una controventatura tradizionale
verticale ad una secondo lo schema Trussed Tube, ideato dall' ing. Khan Fazlur:

Figura 3.23

3) Lo schema tradizionale permette di creare una interconnessione cinematica più
diretta tra i diversi piani della struttura grazie ai legami che si creano nella
struttura a controventi. La lama di controvento resistente a flessione vede
aumentata la sua sezione perciò anche la sua rigidezza flessionale. Non esiste un
legame cinematico diretto tra i nodi dei diversi controventi.

Figura 3.24

4) Lo schema Truss Tube dei controventi instaura un legame cinematico tra tutti i
nodi dei controventi ottenendo cosi un abbattimento dei drift della struttura.
Questo legame prevede una relazione diretta tra lo spostamento relativo dei nodi
che si trovano sull’asse del controvento.

Figura 3.25

Roma, LUGLIO 2013

Pagina 53

A.A. 2012/2013

3.3.2.2
3.3.2.2.1


Flessionale
Risposta strutturale
1) Tipici elementi a comportamento flessionale sono le travi e le piastre che esse
possiedono un comportamento flessibile allo stato limite di esercizio e un
comportamento duttile allo stato limite ultimo. Risulta quindi necessario
ottimizzare il comportamento degli elementi per ridurre le deformazioni
eccessive.
2) Per ottimizzare il comportamento flessionale si specializzano nella struttura delle
parti che devono trasmettere e resistere allo stato tensionale di flessione.
3) In riferimento una struttura sottoposta ad un carico orizzontale vediamone il
comportamento flesso-tagliante con la formazione di due campi di spostamento.

Figura 3.26

4) Il primo campo di spostamenti è quello proveniente dal comportamento
flessionale, il quale può essere studiato e approssimato con elementi alla
Bernoulli; mentre il secondo campo di spostamenti proviene del comportamento
tagliante, il quale può essere studiato e approssimato con elementi alla
Timoshenko.
5) Si affidano i diversi comportamenti deformativi della struttura a elementi diversi: il
comportamento flessionale a un elemento rigido flessionalmente come un vano
ascensore, e il comportamento tagliante al resto della struttura attraverso l’uso di
telai “shear type”.

Figura 3.27

Roma, LUGLIO 2013

Pagina 54

A.A. 2012/2013

3.3.2.2.2
3.3.2.2.2.1


Aspetti tecnologici
Outrigger in sommità
1) Sotto l'azione dei carichi orizzontali, come visto, la deformata della struttura è
sostanzialmente quella di una mensola incastrata.
2) Essendo il sistema iperstatico, gli elementi verticali si caricano proporzionalmente
alla loro rigidezza quindi le colonne di spigolo, essendo usualmente più rigide,
risultano più sollecitate quindi più deformate delle altre con conseguente
deformazione di ogni livello non piana.
3) Tale fenomeno è detto Shaer-Lag, ovvero la sezione della struttura non ruota
rimanendo ortogonale all'asse durante la deformazione e ne consegue una
distribuzione delle tensioni maggiore agli spigoli.

Figura 3.28

4) Per ovviare a tale problema, si può inserire un outrigger in sommità che garantisca
la rigidezza di piano e la deformazione uniforme e piana.

Figura 3.29

3.3.2.2.2.2

Irrigidimenti strutturali
1) La limitazione della deformazione flessionale e degli spostamenti può essere
raggiunta mediante l'inserimento di irrigidimenti degli elementi verticali della
struttura lungo tutto il suo sviluppo. E' evidente che tali elementi generano una
ridistribuzione delle tensioni proporzionale alla nuova disposizione delle rigidezze.

Roma, LUGLIO 2013

Pagina 55

A.A. 2012/2013


2) Gli ispessimenti possono essere di due tipologie:
• Esterne: si aumentano le sezioni degli elementi esterni in modo da ottenere il
vanataggio di centrifugare maggiormente le masse

Figura 3.30

•

Tubolari: si realizza uno schema con costolature interne che formano una
scacchiera su tutta la pianta dell'opera. Il funzionamento del fascio di tubi non
è omogeneo: quelli inteni sono progettati per resistere ai carichi verticali
mentre quelli esterni per i carichi orizzontali:

Figura 3.31

Roma, LUGLIO 2013

Pagina 56


A.A. 2012/2013

SEZIONE 4

PROGETTAZIONE IN ZONA SISMICA

4.1

Introduzione
1) La progettazione delle strutture in zona sismica può prevedere due diverse
tipologie costruttive, in funzione della filosofia progettuale che si sceglie di
adottare:

Figura 4.1

Filosofia
progettuale

Innovativa o
avanzata

Tradizionale

Dissipative
(sfruttamento
duttilità/plasticità)

Non dissipative
(campo elastico)

2) Nella pratica attuale si utilizza il Metodo Dissipativo Semplificato, che rientra nei
metodi tradizionali e permette una progettazione economicamente sostenibile
contando sulle risorse plastiche della struttura in maniera semplice.

4.2

Metodo dissipativo semplificato
1) Il Metodo dissipativo semplificato ha come obiettivo la realizzazione di una
struttura a comportamento dissipativo, ovvero in grado di dissipare molta energia
grazie alla plasticizzazione prima di giungere al collasso.
2) Le plasticizzazioni sono localizzate dal progettista mediante l'inserimento di
elementi appositi in grado di deformarsi molto e dissipare energia, preservando
l'integrità degli elementi a comportamento fragile che vengono progettati per
rimanere in campo elastico.

Figura 4.2

Roma, LUGLIO 2013

Pagina 57

A.A. 2012/2013


3) La modellazione del comportamento dissipativo avviene mediante una
metodologia semplificata che prevede:
• Assicurare la duttilità locale nelle zone dissipative
• Assicurare che le plasticizzazioni avvengano dove progettate mediante il
criterio della gerarchia delle resistenze
• Considerare le risorse plastiche della struttura in maniera indiretta mediante il
fattore di struttura

4.2.1
4.2.1.1

Duttilità locale
Materiale
1) In materiale utilizzato deve soddisfare i seguenti requisiti:
݂௨
≥ 1.2 ߝ௨,௟௔௕௢௥௔௧௢௥௜௢ ≥ 20%
݂௬

2) Per tener conto di possibili errori nella stima della tensione di snervamento, si
maggiora con un coefficiente di sovraresistenza. Questo fa si che gli elementi più
piccoli, caratterizzati da un tasso di lavoro più elevato, garantiranno la dissipazione
energetica tramite la loro plasticizzazione.
S235 → ݂௬ௗ = ݂௬ ∗ 1.12
S235 → ݂௬ௗ = ݂௬ ∗ 1.15

4.2.1.2

Sezione
1) La classificazione delle sezioni è basata sul "element model" (Winter 1947) che
considera la sezione come un insieme di lastre indipendenti, soggette a diverse
condizioni di carico e vincolo .In sostanza si classificano preliminarmente le lastre
compresse, in tutto o parte, e si attribuisce quindi alla sezione la classe
dell'elemento più sfavorevole.
2) Le sezioni si classificano in:
1. Duttile: sviluppano la cerniera plastica perfetta ovvero sono in grado di
raggiungere la resistenza plastica e mantenere invariato il livello resistivo
al ripetersi dei cicli
2. Compatta: sviluppano il momento resistente plastico ma hanno bassa
capacità rotazionale per il subentrare di fenomeni di instabilità locale.
3. Semi-compatta: l'instabilità locale si verifica nella fase intermedia tra
quella corrispondente alla prima plasticizzazione e quella di
plasticizzazione completa
4. Snella: l'instabilità locale si verifica in campo elastico, ovvero prima del
raggiungimento della tensione limite elatica nei punti più sollecitati.

Roma, LUGLIO 2013

Pagina 58


A.A. 2012/2013

Figura 4.3

4.2.2

Fattore di struttura (q)
1) Il fattore di struttura è un coefficiente che permette di progettare con un analisi
elastica contando però sulle capacità plastiche della struttura.
2) Tale risultato si ottiene utilizzando come azioni di progetto le forze elastiche
abbattute mediante un indice di duttilità della struttura in modo da tenere in
considerazione l'ingresso in campo plastico.
3) Il principio alla base della derivazione del fattore di struttura è quello dell'egual
spostamento tra un oscillatore a comportamento elastico e uno a comportamento
elastoplastico: giunti alla stesso livello deformativo ultimo, l'oscillatore
elastoplastico sviluppa una forza molto minore.

Figura 4.4

‫ݍ = ݍ‬଴ ∗ ߞଵ =

ߙ௘ ߙ௨ ߙ ௘
∗
= ݅݊݀݅ܿ݁ ݀݅ ݀‫ݐ݈݅݅ݐݐݑ‬à
ߙ௨ ߙଵ ߙଵ

4) Il fattore di struttura si valuta in funzione della tipologia struttura, del grado di
iperstaticità e dai criteri di progettazione adottati secondo l'espressione:
‫ݍ = ݍ‬଴ ∗ ‫ܭ‬஽ ∗ ‫ܭ‬ோ
Roma, LUGLIO 2013

Pagina 59

A.A. 2012/2013

4.2.2.1


Indice di duttilità (q0)
1) L'indice di duttilità è fornito dalla normativa in funzione della tipologia strutturale
in esame:
• Intelaiate:sono composte da telai che resistono alle forze orizzontali con un
comportamento prevalentemente flessionale. In queste strutture le zone
dissipative sono principalmente collocate alle estremità delle travi in
prossimità dei collegamenti trave-colonna, dove si possono formare cerniere
plastiche e l'energia viene dissipata per mezzo della flessione ciclica plastica

Figura 4.5

.
•

Controventi concentrici: le forze orizzontali sono assorbite principalmente da
membrature soggette a forze assiali e le zone dissipative si concentrano nelle
diagonali tese. Nei controventi a V il punto di intersezione delle diagonali giace
su di una membratura orizzontale che deve essere continua.

•

Controventi eccentrici: le forze orizzontali sono principalmente assorbite da
membrature caricate assialmente, ma la presenza di eccentricità di schema
permette la dissipazione di energia nei traversi per mezzo del comportamento
ciclico a flessione e/o taglio. I controventi eccentrici possono essere classificati
come dissipativi quando si raggiunge la plasticizzazione dei traversi a flessione
e/o taglio, senza superare la resistenza ultima delle altre parti stutturali
(diagonali e colonne).

Figura 4.6

Figura 4.7

Roma, LUGLIO 2013

Pagina 60

A.A. 2012/2013
•


A mensola o a pendolo inverso: sono costituite da membrature le cui zone
dissipative sono posizionate alla base.

Figura 4.8

•

Intelaiate con controventi concentrici: le azioni orizzontali sono assorbite sia
da telai sia da controventi agenti nel medesimo piano
• Intelaiate con tamponature: costituite da tamponature o calcestruzzo non
collegate ma in contatto con le strutture intelaiate
2) La Normativa fornisce il valore dell'indice di duttilità da assegnare in funzione della
tipologia strutturale e dell'approccio progettuale che si vuole adottare, in termini
di entità delle plasticizzazioni sulle quali si vuole contare nel meccanismo
dissipativo:
• Classe di duttilità alta
• Classe di duttilità bassa

Figura 4.9

3) Il valore del rapporto αu/α1 (rapporto tra la deformazione che genera la prima
plasticizzazione e quella ultima) può essere valutato o mediante un'analisi statica
incrementale (pushover) o tramite i valori forniti dalla Normativa:

4.2.2.2

Fattore di regolarità strutturale (KR)
1) Il coefficiente di regolarità strutturale fornisce dei criteri geometrici per definire la
regolarità in pianta e in altezza della struttura in modo da prevenire possibili
collassi locali nelle irregolarità.
• KR = 0.8 Strutture irregolari
• KR = 1 Strutture regolari

Roma, LUGLIO 2013

Pagina 61


A.A. 2012/2013

4.2.2.3

Fattore di duttilità locale (KD)
1) Il coefficiente di duttilità locale è una misura delle caratteristiche della sezione
attraverso il parametro s:
݂௖
‫=ݏ‬
݂௬
in cui ݂௖ è la tensione di collasso e ݂௬ è la tensione di snervamento.
2) I valori del coefficiente di duttilità locale sono riportati nella seguente tabella:
s
>1.2
1<s<1.2
≤1

Membrature
Duttili
Plastiche
Snelle

Figura 4.10

KD
1
0.75
0.5

3) L'espressione del parametro s si specializza in funzione della sollecitazione cui la
membratura è sottoposta:
• Membrature pressoinflesse

ߣ௙ =

‫=ݏ‬
௕೑

ߣ௪ =

௧೑

ܳ=

ܾ௙
ଶ
0.695 + 1.632 ∗ ߣ௙ + 0.062 ∗ ߣଶ − 0.602 ∗ ‫∗ܮ‬
௪
1

೤
∗ ට ா è la snellezza delle ali

ௗೢ,೐
ଶ∗௧ೢ

݀௪,௘ =

݂௖
=
݂௬

ௗೢ
ଶ

ேೞ೏
஺∗௙೤

௙

∗ට

௙೤
ா

è la snellezza dell’anima

∗ ቀ1 + ஺ ∗ ߷ቁ ≤ ݀௪ è l’altezza della parte compressa dell’anima
஺

ೢ

quando la sezione è completamente plasticizzata

è lo sforzo normale adimensionalizzato

‫ ∗ܮ‬è la distanza nella quale so ottiene l’annullamento dello sforzo flessionale

Figura 4.11

Più la sezione è presso-inflessa meno è duttile, più lo sforzo normale è alto più s è
basso e ߣ௪ è alto. Cresce ߷ , cresce ݀௪,௘ , cresce ߣ௪ , diminuisce s.
Roma, LUGLIO 2013

Pagina 62


A.A. 2012/2013
•

Membrature tese

‫ ݊݅݉ = ݏ‬ቊ

݂௨
; 1.25ቋ
݂௬

Figura 4.12

4.2.3

Gerarchia delle resistenze
1) Per gerarchia delle resistenze o capacity design si intende l'insieme di regole da
seguire nella progettazione degli elementi strutturali (travi, pilastri, nodi..) in base
al comportamento e all'importanza che essi assumono nella costruzione.
2) Si cerca di sfruttare la duttilità degli elementi favorendo i meccanismi che possano
sfruttare tale proprietà, come la flessione, rispetto ad altri meccanismi di rottura di
tipo fragile, come il taglio.
3) Inoltre si vuole che i nodi trave/pilastro rimangono sempre nel campo elastico in
quanto difficili da riparare nel caso di danno e si preferisce la rottura di elementi
trave rispetto ai pilastri per evitare il collasso.
4) Tali principi possono essere facilmente concretizzati considerando due modellini
semplici esplicativi di un sistema strutturale composto da elementi fragili e duttili
disposti differentemente:
• In serie:

Figura 4.13

•

In parallelo:

‫ܨ‬ଶ,ோௗ௠௜௡ > ߙ௢௩ ‫ܨ‬ଵ,ோௗ

Figura 4.14

‫ܨ‬ଶ,ோௗ௠௜௡ > ߙ௢௩ ‫ܨ‬ଵ,ோௗ , ݀‫ߙ ݁ݒ݋‬௢௩ è ݈݅ ܿ‫ܽݖ݊݁ݐݏ݅ݏ݁ݎܽݎݒ݋ݏ ݅݀ ݁ݐ݂݂݊݁݅ܿ݅݋‬
.
Roma, LUGLIO 2013

Pagina 63


A.A. 2012/2013

5) Nel caso di una struttura CBF (Concentric Braced Frames):

Figura 4.15

Se le colonne non sono solo compresse ma pressoinflesse:
ܰோௗ ሺ‫ܯ‬௦ௗ ሻ ≥ ܰ௦ௗ,ீ + ߙ௢௩ ∗ ܰ௦ௗ,ா

dove ܰ௦ௗ,ீ è riferito al contributo proveniente dai carichi verticali e ܰ௦ௗ,ா proviene
dal contributo dai carichi sismici. Il coefficiente di sovra-resistenza è:

Dove:
ߛ௢௩ = 1.2

ߙ௢௩ = ݉݅݊ ቊ

ߛ௢௩ ∗ ‫ݏ‬௜ ∗ ܰ௣௟,ோௗ,௜
ቋ
ܰ௦ௗ,௜
௜ୀଵ,…,ே

݂௨
; 1.25ቋ
݂௬
ܰ௣௟,ோௗ,௜ sforzo normale resistente in campo plastico del controventi i-esimo
ܰ௦௟,௜ sforzo normale sollecitante
ܰ numero di controventi nella struttura
‫ݏ‬௜ = ݉݅݊ ቊ

6) Nel caso di una struttura CBF (Concentric Braced Frames):

Figura 4.16

Roma, LUGLIO 2013

Pagina 64


A.A. 2012/2013

ܰோௗ ሺ‫ܯ‬௦ௗ ሻ ≥ ܰ௦ௗ,ீ + ߙ௢௩ ∗ ܰ௦ௗ,ா

ߙ௢௩ = ݉݅݊ ቊ

ߛ௢௩ ∗ ܸ௠,௜ − ܸ௦ௗ,ீ,௜ ߛ௢௩ ∗ ‫ܯ‬௨,௜ − ‫ܯ‬௦ௗ,ீ,௜
;
ቋ
ܸ௦ௗ,ா,௜
‫ܯ‬௦ௗ,ா,௜
௜ୀଵ,..,ே

ఊ೚ೡ ∗௏೘,೔ ି௏ೞ೏,ಸ,೔
௏ೞ೏,ಶ,೔
ఊ೚ೡ ∗ெೠ,೔ ିெೞ೏,ಸ,೔
ெೞ೏,ಶ,೔

‫ܯ‬௦ௗ = ‫ܯ‬௦ௗ,ீ + ߙ௢௩ ∗ ‫ܯ‬௦ௗ,ா

೗೔೙ೖ

per link corti, i queli si plasticizzano a taglio

per link lunghi, i quali si plasticizzano a flessione

7) La progettazione dei collegamenti deve essere realizzata assegnando una
sovraresistenza in quanto il nodo deve avere una resistenza maggiore degli
elementi che vi confluiscono:

Figura 4.17

Roma, LUGLIO 2013

Pagina 65

A.A. 2012/2013

APP. A


COLLASSO PROGRESSIVO
1) Si definisce collasso progressivo la diffusione del del danno locale al resto della
struttura fino a provocare un danno disproporzionato rispetto al danno iniziale
locale.
2) Ne deriva che lo sviluppo prevede innanzitutto una causa (esplosione) che genera
un danno locale che si propaga lungo la struttura.
3) Si distinguono quindi danni diretti, immediatamente conseguenti alla causa, e
danni progressivi, che si sviluppano nel tempo a causa del fallimento di uno degli
elementi che genera una ridistribuzione dei carichi non compatibile con la
struttura.
4) I collassi progressivi si distinguono in:
• Pancake type collapse
Il danno iniziale si realizza negli elementi verticali e le parti sovrastanti cadono,
facendo fallire i livelli più bassi.
• Domino type collapse
La rotazione dalla posizione di equilibrio inziale genera un'impatto con le
strutture affiancate
• Zipper type collapse
Il fallimento di un elemento porta ad un sovraccarico degli elementi adiacenti
che non resistono con conseguente collasso. Si sviluppa nella direzione lunga
della struttura
• Section type collapse
E' equivalente alla modalità di collasso precedente, sviluppata però sul lato
corto della struttura.
5) Nelle prime due modalità il trasferimento di energia avviene per impatto mentre
negli ultimi due per ridistribuzione anche se in generale i due fenomeni sono
coesistenti
6) E' possibile fare un calcolo probabilistico del collasso progressivo ma è
un'operazione molto complessa perchè necessita di una conoscenza approfondita
di tutte le fasi (causa, danno, propagazione), da processare anch'esse dal punto di
vista probabilistico.
7) Lo studio del collasso progressivo è legata molto alla percezione di rischio
dell'utenze perchè si tratta di collassi che storicamente sono stati sempre causati
da attentati terroristici.
8) La progettazione contro il collasso rientra nella metodologia di progettazione
secondaria basata sulle conseguenze, al contrario della progettazione primaria
tradizionale che si basa sulla resistenza ai carichi dei singoli elementi strutturali.
9) E' un problema complesso nel quale un ruolo fondamentale è ricoperto
dall'incertezza che, in questi casi, aumenta perchè parliamo di eventi di bassa
probabilità e alto rischio quindi totalmente opposti alle azioni comuni.

Roma, LUGLIO 2013

Pagina 66


A.A. 2012/2013

Robustezza strutturale
1) Si definisce robustezza strutturale l'abilità della struttura la capacità della struttura
di resistere ad un danno locale.
2) Una struttura molto performante in termini di carico ultimo portato non
necessariamente lo è anche in termini di robustezza in quanto questa ultima
caratteristica va letta non sul sistema integro ma su quello danneggiato.
3) Per aumentare la robustezza di una struttura si ricorre a:
• Ridondanza (alto numero di elementi, iperstaticità esterna ed interna)
• Compartimentazione (suddivisione in parti indipendenti)
4) Per ottenere questi risultati si può agire con metodi differenti:
• Metodi indiretti
Sono prescrittivi sui dettagli costruttivi senza ulteriori analisi non lineari ed è
adatta ad edifici ordinari non esposti a rischio
• Metodo diretto deduttivo
Si applica l'esplosione agli elementi locali, una volta stimatane l'entità, e si
trova la risposta globale
• Metodo diretto induttivo
Prescindendo dal carico, si ipotizza un danno e si valuta la risposta globale e
solo a posteriori si può stimare dal danno l'entità del carico.
5) IL calcolo effettivo della robustezza si effettua ipotizzando un danno (induttivo) e
realizzando un'analisi dinamica sotto i carichi. A questo punto si confrontano i
risultati sulla struttura integra con quelli sulla struttura danneggiata in termini di
rapporto tra i rispettivi moltiplicatori ultimi dei carichi dall'analisi di pushover.
L'analisi viene ripetuta più volte modificando la localizzazione del danno iniziale.
6) Un'analisi di questo tipo serve anche per valutare il Consequence Factor ovvero la
stima dell'importanza di un singolo elemento resistente nel complesso strutturale.

Figura A.1
Robustezza
strutturale

Ridondanza

aumento
degli
elementi
strutturali

Roma, LUGLIO 2013

aumento
gradi vincoli
interni/ester
ni

Compattazione

sizing delle
sezioni

danno rimane
localizzato a
compartiment
i stagni

Pagina 67


A.A. 2012/2013

APP. B

FATICA
1) La fatica è un fenomeno meccanico per cui un materiale sottoposto
a carichi variabili nel tempo (in maniera regolare o casuale"prova ciclica") si
danneggia fino a rottura, nonostante l'intensità massima dei carichi in questione
sia sensibilmente inferiore a quella di rottura o di snervamento statico del
materiale stesso.
2) Tale aspetto è rilevante per strutture sottoposte a carichi critici quali ponti, tralicci
e non per strutture residenziali ordinarie.
3) La fatica e la rottura che ne consegue dipende da:
• profilatura
• lavorazione
• saldature
4) La fatica è dunque funzione delle concentrazioni di tensione presenti nel
particolare costruttivo.
5) L'approccio con cui si studia la fatica è basato sullo studio di elementi testati da
carichi ciclici fino alla rottura. Considerando una lastra tesa:

Figura B.1

Se il pezzo fosse destinato ad essere caricato da una forza monotona costante, il
progetto dello stesso si limiterebbe al dimensionamento della sezione trasversale
tale da generare una tensione interna minore di quella di snervamento.
6) Se, invece, il carico è ciclico, bisogna tener contro della rottura a fatica che è fragile
e da evitare assolutamente quindi si testano i pezzi con variazioni di tensione
ciclica:

Figura B.2

ߪ௠௜௡
ߪ௠௔௫
ܴ = 1 → ߪ௠௜௡ = ߪ௠௔௫ ܿܽ‫݋ܿ݅ݐܽݐݏ ݋ܿ݅ݎ‬
0 < ܴ < 1 → ߪ௠௜௡ > 0 ܿܽ‫݁ݐ݊ܽݏ݈ݑ݌ ݋ܿ݅ݎ‬
ܴ = 1 → ߪ௠௜௡ = 0 ܿܽ‫0 ݋݈݈݁݀ ݁ݐ݊ܽݏ݈ݑ݌ ݋ܿ݅ݎ‬
−1 < ܴ < 0 → −ߪ௠௔௫ < ߪ௠௜௡ < 0 ܿܽ‫݋݊ݎ݁ݐ݈ܽ ݋ܿ݅ݎ‬
ܴ=

Roma, LUGLIO 2013

Pagina 68


A.A. 2012/2013

7) Il risultato delle esperienze empiriche sono le Curve di Wolher e ne esistono per
tutti i dettagli costruttivi e sono indipendenti da R quindi dal tipo di carico:

Figura B.3

Tali curve forniscono il numero di cicli che porta a rottura il pezzo in funzione
dell'incremento di tensione nel pezzo rispetto a quella statica sempre presente nel
pezzo.
8) Per eseguire la verifica a rottura si utilizza la legge del danno cumulato di Miner:
෍

݊௜
=1
ܰ଴

dove, per uno stesso livello di tensione σi, ni è il numero di cicli a cui
effettivamente il pezzo è sottoposto durante la sua storia di carico ed Ni è il
numero di cicli che porta il pezzo a rottura per fatica dalle curve di Wohler.
9) La legge di Miner si basa sull'ipotesi che ogni serie di cicli per un incremento
tensionale consumi parte della capacità resistente a fatica del pezzo
indipendentemente dalla successione temporale degli incrementi stessi.
Quest'ultima ipotesi non è molto realistica in quanto l'entità delle plasticizzazioni
accumulate dipende dal danno precedente che, ovviamente, è proporzionale al
livello di carico corrispondente.
10) Le curve di Wohler sono fornite dal CNR-UNI 10011, riferite a tutti i particolari
costruttivi, soprattutto saldature.

Roma, LUGLIO 2013

Pagina 69

A.A. 2012/2013

APP.C


MODELLAZIONE DI DETTAGLIO
1) In generale la sovrastruttura è composta da elementi di piano, quali travi
principali, secondarie, solai, ecc., e da sezioni verticali, per esempio regioni nodali
e controventi. Ognuna di queste parti, durante la fase di progettazione strutturale,
va schematizzata attraverso dei modelli semplificativi.
2) Il livello di dettaglio che raggiunge un modello non è indicativo della praticità o
utilità della modellazione perché normalmente il processo di raffinazione richiede
l’impiego di tempo e denaro che a volte non giustificano il guadagno totale. Ne
deriva che molte volte conviene invece utilizzare un modello meno raffinato
aumentando i coefficienti di sicurezza.
3) In ogni caso la modellazione può essere spinta ad approfonditi livelli di dettaglio in
presenza di particolari costruttivi critici mediante tre metodi:
• Metodo ad abaco, che rappresenta un modello analitico semplificato
• Metodo delle componenti, caratterizzato da modellini meccanici
• Metodo agli elementi finiti, che è un modello complesso
4) Si riporta un esempio di modellazione di dettaglio per una trave a doppio T forata
nell'anima:

Figura C.1

Il confronto tra i modelli è effettuato stimando il valore della freccia.
•

Prima modellazione
Si modella un elemento monoassiale a sezione costante vincolata da vincoli
perfetti ideali e senza considerare la presenza del foro.

•

Seconda modellazione
Si modella un elemento monoassiale vincolato da vincoli perfetti ideali che
però presenta una variazione di sezione in coincidenza con la presenza del
foro.

Figura C.2

Roma, LUGLIO 2013

Pagina 70

A.A. 2012/2013


Figura C.3

•

Terza modellazione
Si modella un elemento monoassiale identico al precedente con la differenza
di dividere il contributo del foro tra ala superiore e ala inferiore:

•

Quarta modellazione
Si modella una trave 2D mediante elementi finiti, rispettando fedelmente la
geometria iniziale:

Figura C.4

Figura C.5

5) E' evidente che l'aumento della complessità del problema non è proporzionale al
miglioramento dei risultati ottenuti. Ne deriva che spingere la modellazione ad un
elevato livello di dettaglio è giustificata solo in casi particolari e non nella
progettazione di lementi tradizionali.

Roma, LUGLIO 2013

Pagina 71

FACULTY OF CIVIL AND INDUSTRIAL ENGINEERING

Department of Structural and Geotechnical Engineering

A.A. 2012 – 2013
Course:

Steel Constructions

Exercises

Professor:
Assistants:

Rome, AUGUST 2013

Student:

Steel Construction - Exercises
A.A. 2012/2013

Professor: Prof. Franco Bontempi
Assistants: Ing. Francesco Petrini

INDEX
PART A: PLASTIC BEHAVIOR
EXERCISE N.1: RETICULAR SYSTEM OF THREE TRUSS BEAMS ....................................................... 1
1.1 Outline ................................................................................................................................. 1
1.2 Analytical method ................................................................................................................ 1
1.2.1 Loading phase ....................................................................................................................................... 2
1.2.1.1 Elastic solution ............................................................................................................................. 2
1.2.1.1.1 Congruence .......................................................................................................................... 2
1.2.1.1.2 Constitutive equation........................................................................................................... 2
1.2.1.1.3 Equilibrium ........................................................................................................................... 2
1.2.1.1.4 Solution ................................................................................................................................ 2
1.2.1.2 Plastic solution ............................................................................................................................. 3
1.2.1.2.1 Congruence .......................................................................................................................... 3
1.2.1.2.2 Constitutive equation........................................................................................................... 3
1.2.1.2.3 Equilibrium ........................................................................................................................... 3
1.2.1.2.4 Solution ................................................................................................................................ 3
1.2.2 Unloading phase ................................................................................................................................... 4

1.3 Incremental method ............................................................................................................. 5
1.3.1 SAP2000................................................................................................................................................ 5
1.3.1.1 Modeling ...................................................................................................................................... 5
1.3.1.2 Loading phase............................................................................................................................... 6
1.3.1.3 Unloading phase........................................................................................................................... 8

1.4 Comparison ......................................................................................................................... 9
EXERCISE N.2: PLANE STRUCTURE ............................................................................................. 10
2.1 Outline ............................................................................................................................... 10
2.2 Limit analysis ...................................................................................................................... 11
2.2.1 Kinematic theorem .............................................................................................................................11
2.2.2 Application of uniqueness theorem ...................................................................................................12

2.3 Incremental method ........................................................................................................... 13
2.3.1 SAP2000..............................................................................................................................................13
2.3.1.1 Modeling ....................................................................................................................................13
2.3.1.2 Flexural plastic hinges ................................................................................................................14
2.3.1.2.1 Results ................................................................................................................................15
2.3.1.3 Buckling plastic hinges ...............................................................................................................16
2.3.1.3.1 Results ................................................................................................................................17
2.3.1.4 Comparison ................................................................................................................................19

EXERCISE N.3: FIXED-ENDS BEAM WITH DISTRIBUTED LOAD ..................................................... 20
3.1 Outline ............................................................................................................................... 20
Rome, AUGUST 2013

A.A. 2012/2013


3.2 Analytical method .............................................................................................................. 21
3.2.1 Elastic solution ..................................................................................................................................21
3.2.1.1 Congruence ................................................................................................................................21
3.2.1.2 Constitutive equation .................................................................................................................21
3.2.1.3 Equilibrium .................................................................................................................................21
3.2.1.4 Solution ......................................................................................................................................21
3.2.2 Plastic solution....................................................................................................................................22
3.2.2.1 Congruence ................................................................................................................................23
3.2.2.2 Constitutive equation .................................................................................................................23
3.2.2.3 Equilibrium .................................................................................................................................23
3.2.2.4 Solution ......................................................................................................................................23
3.2.3 Length of plastic hinge .......................................................................................................................24

3.3.1 SAP2000..............................................................................................................................................25
3.3.1.1 Modeling ....................................................................................................................................25
3.3.1.2 Analysis .......................................................................................................................................26
3.3.1.3 Results ........................................................................................................................................27

EXERCISE N.4: PLANE STRUCTURE WITH TWO FLOORS .............................................................. 30
4.1 Outline ............................................................................................................................... 30
4.2.1 SAP2000..............................................................................................................................................31
4.2.1.1 Modeling ....................................................................................................................................31
4.2.1.2 Flexural plastic hinges ................................................................................................................32
4.2.1.2.1 Results ................................................................................................................................33
4.2.1.3 Buckling plastic hinges ...............................................................................................................36
4.2.1.3.1 Results ................................................................................................................................37
4.2.1.4 Comparison ................................................................................................................................40

PART B: BUCKLING
EXERCISE N.5: CRITICAL AND POST-CRITICAL BEHAVIOR OF A BOUNDED BEAM WITH
CONCENTRATED LOAD ............................................................................................................. 41
5.1 Outline ............................................................................................................................... 41
5.2 Case A ................................................................................................................................ 41
5.2.1 Analytical method ..............................................................................................................................41
5.2.1.1 Ideal beam ..................................................................................................................................42
5.2.1.1.1 Small displacements...........................................................................................................42
5.2.1.1.2 Large displacements ..........................................................................................................42
5.2.1.2 Real beam ...................................................................................................................................42
5.2.1.3 Results ........................................................................................................................................43
5.2.2 Incremental method...........................................................................................................................43
Rome, AUGUST 2013

A.A. 2012/2013


5.2.2.1 Real Beam...................................................................................................................................43
5.2.2.1.1 SAP2000 .............................................................................................................................43
5.2.2.1.1.1 Modeling ...................................................................................................................43
5.2.2.1.1.2 Results ......................................................................................................................44

5.3 Case B ................................................................................................................................ 46
5.3.1.1 Ideal beam ..................................................................................................................................46
5.3.1.2 Real beam ...................................................................................................................................47
5.3.1.3 Results ........................................................................................................................................48
5.3.2.1 Real Beam...................................................................................................................................48
5.3.2.1.1 SAP2000 .............................................................................................................................48
5.3.2.1.1.1 Modeling ...................................................................................................................48
5.3.2.1.1.2 Results ......................................................................................................................48

5.4 Case C................................................................................................................................. 50
5.4.1.1 Ideal beam ..................................................................................................................................51
5.4.1.2 Real beam ...................................................................................................................................52
5.4.1.3 Results ........................................................................................................................................52
5.4.2.1 Real Beam...................................................................................................................................54
5.4.2.1.1 SAP2000 .............................................................................................................................54
5.4.2.1.1.1 Modeling ...................................................................................................................54
5.4.2.1.1.2 Results ......................................................................................................................54

EXERCISE N.6: EVOLUTION OF THE LOAD-DISPLACEMENT CURVE OF A THREE-HINGED ARCH ..... 58
6.1 Outline ............................................................................................................................... 58
6.2 Analytical method .............................................................................................................. 59
6.2.1 Congruence .......................................................................................................................................59
6.2.2 Constitutive equation........................................................................................................................59
6.2.3 Equilibrium ........................................................................................................................................59
6.2.4 Solution .............................................................................................................................................60

6.3.1 SAP2000..............................................................................................................................................61
6.3.1.1 Modeling ....................................................................................................................................61
6.3.1.2 Analysis .......................................................................................................................................62
Rome, AUGUST 2013

Exercise n.1: Reticular system of three truss beams

A.A. 2012/2013

Plastic Behavior

EXERCISE N.1

RETICULAR SYSTEM OF THREE TRUSS BEAMS

1.1

Outline
1) Assuming an elastic perfectly plastic-type behavior, evaluate critical load of the
structure in Figure 1.1 analytically and compare it with that obtained using nonlinear incremental static analysis obtained with a computational code. Carry out,
also, the study of the unloading phase and, if possible, a step of re-load in order to
highlight the cyclic behavior. In the study use plastic hinges axial or plasticity
widespread.

L

Fiugure 1.1

σ

fy

L

2

1

3

45°

εy

εu ε

P

Aste con sezione
circolare

d=10 cm

2) Material data:
• ‫݉݉/ܰ 000012 = ܧ‬ଶ ‫ݏݏ݂݂݁݊݅ݐݏ ܿ݅ݐݏ݈ܽܧ‬
• ݂௬ = 240 ܰ/݉݉ଶ ܻ݈݅݁݀ ‫ݏݏ݁ݎݐݏ‬
•

•

ߝ௬ =

ா
௙೤

= 0,11429 % ܻ݈݅݁݀ ‫݊݅ܽݎݐݏ‬

ߝ௨ = 5 % ܷ݈‫݊݅ܽݎݐݏ ݁ݐܽ݉݅ݐ‬

3) Geometry data:
• ‫ݐ݈݃݊݁ ݉ܽ݁ܤ ݉ 5 = ܮ‬ℎ
• ‫ݎ݁ݐ݁݉ܽ݅݀ ݉ܽ݁ܤ ݉ܿ 01 = ܦ‬
•

‫=ܣ‬

గ஽ మ
ସ

= 7850 ݉݉ଶ ܵ݁ܿ‫ܽ݁ݎܽ ݊݋݅ݐ‬

4) For all beams the value of yield axial force is:

5) System hyperstaticity is 1

1.2

ܰ௬ = ݂௬ ∗ ‫ܰ݇ 59.4881 = ܣ‬

Analytical method
1) We indicate with:
• X : axial force of beam 1
• Y : axial force of beam 2 and 3
• δ : vertical displacement of node O

Rome, AUGUST 2013

Pag. 1


A.A. 2012/2013

Plastic Behavior
2) We apply the Displacement Method, or rather we derive equilibrium equations,
written in terms of displacements, substituting the constitutive relationship and
kinematic compatibility in equilibrium equations written in terms of stress.
3) We make the assumption of little displacements, so we can write the equilibrium
equation in the undeformed shape.

Figure 1.2

1.2.1
1.2.1.1

Loading phase
Elastic solution
1) We find the elastic solution, when, in the first load phase, element stresses are so
low that prevent the passage in plastic range and we derive the first yield load Py

1.2.1.1.1

Congruence
1) We write congruence equations, indicating with L2 and ΔL2 respectively the initial
length and the stretch of beam 2 and 3.
•
•

1.2.1.1.2

Beam 1: ߜ = ‫ߝ ∗ ܮ‬ଵ → ߝଵ =
௅
ఋ

Beam 2-3: ߂‫ܮ‬ଶ = ‫ܮ‬ଶ ∗ ߝଶ → ߜ ∗ cos ସ =
గ

௅
ഏ
ୡ୭ୱ
ర

Constitutive equation

∗ ߝଶ → ߝଶ = ଶ௅
ఋ

1) We write constitutive equation in elastic range:

•
•

1.2.1.1.3

1.2.1.1.4

ߪ = ‫ߝ ∗ ܣܧ = ܰ ߝ ∗ ܧ‬

Beam 1: ‫ߝ ∗ ܣܧ = ݔ‬ଵ =

ா஺
௅

∗ ߜ

Beam 2-3: : ‫ߝ ∗ ܣܧ = ݕ‬ଶ =
ଶ

ଵ ா஺
௅

∗ ߜ = ଶ ∗ ‫ݔ‬
ଵ

Equilibrium
1) We write the equilibrium equation to the vertical translation of node O (the
horizontal balance is automatically guaranteed because we assumed that stresses
of beam 2 and 3 are the same).
ߨ
‫ ∗ ݕ2 + ݔ‬cos = ܲ
4

Solution

1) Combining previous equations, we find:
‫ۓ‬

‫ݕ2 = ݔ‬

‫= ݔۓ‬

→
√2
=ܲ
‫ݕ2 + ݔ۔‬
‫= ݕ۔‬
2
‫ە‬
‫ە‬
Rome, AUGUST 2013

2ܲ

2 + √2

ܲ
2 + √2

Pag. 2


A.A. 2012/2013

Plastic Behavior
2) Beam 1 is the first to reach the plastic range when:

‫ݔ = ݔ‬௬ = ܰ௬ = 1884.92 ݇ܰ
This value of axial force is reached when:

2 + √2
ܰ௬ = 3217.82 ݇ܰ
2
For the same value of load, axial force in beam 2 and 3 is:
ܲ = ܲ௬ =

1
‫ݕ = ݕ‬௬ = ‫ݔ‬௬ = 942.48 ݇ܰ < ܰ௬
2

3) The corresponding displacement δ and related beam strains are:
ߜ = ߜ௬ =

•
•

1.2.1.2

‫ܮ‬
‫ܮ‬
ܰ௬ = ݂௬ = 5.71 ݉݉
‫ܣܧ‬
‫ܧ‬

Beam 1: ߝଵ = ߝ௬ = 0.11429 %

Beam 2-3: ߝଶ = ଶ ௅ = 0.05714 %
ଵ ఋ

Plastic solution
1) We find the plastic solution and the ultimate load Pcr, considering that beam 1 is
completely in plastic range, so its stress can't increase more and is equal to Ny.

1.2.1.2.1

1.2.1.2.2

Equilibrium
1) As we did previously, we write the equilibrium equation to the vertical translation
of node O:
ߨ
ߨ
‫ ∗ ݕ2 + ݔ‬cos = ܲ → 2‫ ∗ ݕ‬cos = ܲ − ݂௬ ∗ ‫ܣ‬
4
4

Solution

1) Solution equations become:

‫ݔ = ݔ‬௖௥ = ܰ௬ = ݂௬ ∗ ‫ܣ‬
ܲ − ݂௬ ∗ ‫ܣ‬

ቐ
‫=ݕ‬
√2

2) Beam 2 and 3 reach together plastic range when their axial force become equal to:
‫ݕ = ݕ‬௖௥ = ܰ௬ = 1884.92 ݇ܰ

This value of axial force is reached when:

ܲ = ܲ௖௥ = ݂௬ ∗ ‫ܰ݇ 96.0554 = )2√ + 1( ∗ ܣ‬

3) The corresponding displacement δ and related beam strains are:

•
•

Beam 1: ߝଵ = ߝ௬ +

ߜ = ߜ௖௥ = 2
ఋ೎ೝ ାఋ೤

‫ܮ‬
ܰ = 11.43 ݉݉
‫ ܣܧ‬௬

= 0.22857 %

Beam 2-3: ߝଶ = ߝ௬ = 0.11429 %
௅

This is the correct solution because beam 1 strain is lower than failure strain εcu.

Rome, AUGUST 2013

Pag. 3


A.A. 2012/2013

Plastic Behavior
4) Plastic resources of structure in terms of load P are equal to:

ܲ௖௥ ݂௬ ∗ ‫)2√ + 1( ∗ ܣ‬
=
= 1.414 → ܱ‫ݐ݃݊݁ݎݐݏݎ݁ݒ‬ℎ = 41.4%
ܲ௬
2 + √2
݂௬ ∗ ‫2 ∗ ܣ‬

Equally, in terms of displacement δ

1.2.2

Unloading phase

‫ܮ‬
ߜ௖௥ 2 ‫݂ ܧ‬௬
=
= 2.0 → ‫%001 = ݕݐ݈݅݅ݐܿݑܦ‬
‫ܮ‬
ߜ௬
݂௬
‫ܧ‬

1) Assuming that unloading phase starts before Pcr is reached and that the last value
of load is 0, we find system solution in this step:
∆ܲ = −ܲ௖௥ = −݂௬ ∗ ‫ ∗ ܣ‬൫1 + √2൯ = −4550.69 ݇ܰ → ܲ௥ = 0

2) During the unloading phase, beams behavior is elastic, because we assume an
elastic perfectly plastic-type constitutive relationship.
‫= ݔ∆ۓ‬

→
ቐ
√2
∆‫ݕ∆2 + ݔ‬
= ∆ܲ
‫= ݕ∆ ۔‬
2
‫ە‬
∆‫ݕ∆2 = ݔ‬

2ܲ

2 + √2
ܲ

2 + √2

=−
=−

2 + √2

ܲ௖௥
2ܲ௖௥

2 + √2

3) We find beam residual stresses:
‫ ∗ ܣ ∗ ݂ = ݔ∆ − ݔ = ݔۓ‬൭1 − 2 ൫1 + √2൯൱ = −780.77 ݇ܰ
௖௥
௬
ۖ ௥
2 + √2
‫۔‬
2
൫1 + √2൯൱ = 552.09 ݇ܰ
ۖ ‫ݕ‬௥ = ‫ݕ‬௖௥ − ∆‫݂ = ݕ‬௬ ∗ ‫ ∗ ܣ‬൭1 −
2 + √2
‫ە‬

4) Beam 1 stays compressed till the end of the unloading phase, because it had
already reached plastic range before the beginning of this step, with plastic strain
equal to:
ߝ௖௥ − ߝ௬ = 0.11429%
At the end of unloading phase, beam 1 residual strain is:
ߝ௥ଵ = ߝ௬ −

∆‫ݔ‬
= 0.0669%
‫ܣܧ‬

This means that residual displacement of node O is:

ߜ = ߜ௥ = ‫ߝ ∗ ܮ‬௥ = 3,35 ݉݉

5) Beam 2 and 3 result stretched to respect congruency:
ߝ௥ଶ =

ߜ௥
= 0.0335%
2‫ܮ‬

Beam 1 is necessary compressed to balance all forces because, as we said, the final
value of load is 0.
6) We draw the evolution of beam axial forces at varying of loads:

Rome, AUGUST 2013

Pag. 4


A.A. 2012/2013

Plastic Behavior

Figure 1.3

Evolution of axial forces
1,50
+ 41.4 %
1,25
B

A'

N/(fy A)

1,00
0,75
0,50

A''

C''

0,25
0,00
-0,25

0,00 0,25 0,50 0,75 1,00 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3,00

-0,50

C'

P/(fy A)
Beam 1
Beam 2-3
Unload step beam 1
Unload step beam 2-3

When beam 1 reaches plastic range, axial force in beam 2 and 3 is half that of the
beam 1, so it is half the yield strength.
7) We draw the evolution of node O displacement δ at varying of load:

Figure 1.4

P (kN)

Load- Displacement
5000,00
4500,00
4000,00
3500,00
3000,00
2500,00
2000,00
1500,00
1000,00
500,00
0,00

B

A

C
0,00

2,50

5,00
Load step

1.3
1.3.1
1.3.1.1

7,50

10,00
Unload step

12,50

15,00
δ (mm)

Incremental method
SAP2000
Modeling
1) The structure is modeled by frame elements with material and section properties
previously indicated. Every beam is bounded by external hinge.
2) We apply a vertical force P=1 kN in node O, that will be used to set push-over
analysis.

Rome, AUGUST 2013

Pag. 5


A.A. 2012/2013

Plastic Behavior
3) We assign to every beam an axial hinge, defined in terms of stress-strain, at the half
of the length (in this case hinge's position is not important because stress state is
uniform across the beam).
4) We define a nonlinear static load case called Pushover P, that uses the base load
pattern P previously defined. This is a displacement control analysis in which we
monitor node O displacement.

1.3.1.2

Loading phase
1) We report the results:

Figure 1.5

Multiplier Displacement Axial Force Beam 1 Axial force Beam 2-3
Step λ (kN)
δ (mm)
N1 (kN)
N2 (kN)
0
0,00
0,00
0,00
0,00
1
3217,83
5,71
1884,96
942,48
2
4550,70
11,43
1884,96
1884,96
3
4550,76
111,43
1885,00
1884,98
4
4550,81
211,43
1885,03
1884,99
5
4550,84
255,75
1885,04
1885,00
6
4550,84
255,75
1885,04
1885,00
7
2665,83
307,18
0,02
1885,01
8
2665,88
407,18
0,05
1885,03
9
2665,94
507,18
0,09
1885,04
10 2665,94
507,18
0,09
1885,04
11
0,15
610,04
0,12
0,02
12
0,20
710,04
0,15
0,04
13
0,26
810,04
0,19
0,05
14
0,31
910,04
0,22
0,07
15
0,37
1000,00
0,25
0,08

Figure 1.6

Rome, AUGUST 2013

Pag. 6


A.A. 2012/2013

Plastic Behavior

Figure 1.7

Figure 1.8
1,50

+ 41.4 %

1,25

A'

N/(fy A)

1,00
0,75

B
Beam 1

0,50

A''
Beam 2-3

0,25
0,00
0,00 0,25 0,50 0,75 1,00 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3,00
P/(fy A)

2) We show formation order of the hinges, during fundamental steps of the analysis
(from formation of first hinge in beam 1 to the failure of structure)

Figure 1.9

Rome, AUGUST 2013

Pag. 7


A.A. 2012/2013

1.3.1.2

Plastic Behavior

Unloading phase
1) We define two linear nonstatic load cases to perform analysis during unloading
phase.
2) First one is exactly the same as that previously defined, with the only difference
that we stop analysis when node O displacement reaches a slightly lower value than
the failure one. Therefore, ultimately, we do a displacement control analysis setting
the ultimate displacement of node O at the value of 11 mm.
3) Second load case is defined starting form the final state of the first one, assigning a
force to the structure in the opposite direction.

Unload phase

Load phase

Figure 1.10

Rome, AUGUST 2013

Multiplier Displacement Axial Force Beam 1 Axial force Beam 2-3
Step λ (kN)
δ (mm)
N1 (kN)
N2 (kN)
0
0,00
0,00
0,00
0,00
1
619,43
1,10
362,86
181,43
2
1238,86
2,20
725,71
362,86
3
1858,30
3,30
1088,56
544,28
4
2477,73
4,40
1451,42
725,71
5
3097,16
5,50
1814,27
907,14
6
3217,83
5,71
1884,96
942,48
7
3474,41
6,81
1884,96
1123,91
8
3730,98
7,91
1884,96
1305,34
9
3987,56
9,01
1884,96
1486,76
10 4244,14
10,11
1884,96
1668,19
11 4450,73
11,00
1884,96
1814,27
12 4450,73
11,00
1884,96
1814,27
13 3887,61
10,00
1555,10
1649,34
14 3324,50
9,00
1225,23
1484,41
15 2761,38
8,00
895,36
1319,47
16 2198,26
7,00
565,49
1154,54
17 1635,14
6,00
235,62
989,60
18 1072,02
5,00
-94,25
824,67
19
508,90
4,00
-424,11
659,74
20
0,00
3,10
-722,22
510,68

Pag. 8


A.A. 2012/2013

Plastic Behavior

Figure 1.11

P (kN)

Load - Displacement
5000,00
4500,00
4000,00
3500,00
3000,00
2500,00
2000,00
1500,00
1000,00
500,00
0,00

B

Carico

A

Scaric
o

C
0,00

2,50

5,00

7,50

10,00

12,50

15,00

δ (mm)


Figure 1.12
1,50
1,25

A'

N/(fy A)

1,00

B

0,75
0,50

A''

C''

0,25
0,00
-0,25 0,00 0,25 0,50 0,75 1,00 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3,00
P/(fy A)
C'
-0,50
Beam 1
Unload step beam1

1.4

Beam 2-3
Unload step beam 2-3

Comparison
1) We report the comparison of results between the two different analyzes:
P

Figure 1.13

δ

P/Ny

x/Ny

y/Ny

Point
An.
Increm. An. Increm. An. Increm. An. Increm. An. Increm.
O
0,00
0,00
0,00
0,00 0,00 0,00
0,00 0,00 0,00 0,00
A 3217,82 3217,82 5,71
5,71 1,71 1,71
1,00 1,00 0,50 0,50
B 4550,69 4550,69 11,43 11,43 2,41 2,41
1,00 1,00 1,00 1,00
C
0,00
0,00
3,35
3,10 0,00 0,00 -0,41 -0,38 0,29 0,27

Rome, AUGUST 2013

Pag. 9

Exercise n.2: Plane frame

A.A. 2012/2013

Plastic Behavior

EXERCISE N.2

PLANE STRUCTURE

2.1

Outline
1) Assuming an elastic perfectly plastic-type behavior ,analytically evaluate the
ultimate load multiplier and compare it with that calculated by a computational
code with an appropriate analysis. Evaluate, also, the push-over curve. In the study
use plastic hinges axial or plasticity widespread. Implement, finally, buckling to
plastic hinges.
VV

Figure 2.1

H= 0.8 H
V

C
C

D
D

L

A

B

A

B

L

L

Figure 2.2

2) Material data:
• ‫݉݉/ܰ 000012 = ܧ‬ଶ ‫ݏݏ݂݂݁݊݅ݐݏ ܿ݅ݐݏ݈ܽܧ‬
• ݂௬௞ = 235 ܰ/݉݉ଶ ܻ݈݅݁݀ ‫ݏݏ݁ݎݐݏ‬
•

•
•

݂௬ௗ =

ߝ௬ௗ =

௙೤ೖ

ఊಾబ
௙೤೏

= 223.81 ܰ/݉݉ଶ ‫ݏݏ݁ݎݐݏ ݈݀݁݅ݕ ݊݃݅ݏ݁ܦ‬

= 0,10658 % ‫݊݅ܽݎݐݏ ݈݀݁݅ݕ ݊݃݅ݏ݁ܦ‬

ߝ௨ = 5 % ܷ݈‫݊݅ܽݎݐݏ ݁ݐܽ݉݅ݐ‬
ா

3) Geometry data:
• ‫ݐ݈݃݊݁ ݉ܽ݁ܤ ݉ 5 = ܮ‬ℎ
4) Section geometry data:
• ܾ = 100 ܿ݉ ‫ݐ݀݅ݓ ݈݁݃݊ܽܨ‬ℎ
• ℎ = 200 ܿ݉ ܵ݁ܿ‫݃݅݁ܪ ݊݋݅ݐ‬ℎ‫ ݐ‬
Rome, AUGUST 2013

Pag. 10


A.A. 2012/2013

Plastic Behavior
•
•
•
•
•
•
•

‫݉ܿ 5.82 = ܣ‬ଶ ܵ݁ܿ‫ܽ݁ݎܽ ݊݋݅ݐ‬
ℎ = 200 ܿ݉ ܵ݁ܿ‫݃݅݁ܪ ݊݋݅ݐ‬ℎ‫ ݐ‬
‫ݐ‬௙ = 8.5 ݉݉ ‫ݐ ݈݁݃݊ܽܨ‬ℎ݅ܿ݇݊݁‫ ݏݏ‬

‫ݐ‬௪ = 5.6 ݉݉ ܹܾ݁ ‫ݐ‬ℎ݅ܿ݇݊݁‫ ݏݏ‬
‫݉ܿ 0.3491 = ܫ‬ସ ‫ ܽ݅ݐݎ݁݊ܫ‬
ܹ௘௟ = 194.0 ܿ݉ଷ ‫ ݏݑ݈ݑ݀݋݉ ݊݋݅ݐܿ݁ݏ ܿ݅ݐݏ݈ܽܧ‬
ܹ௣௟ = 221.0 ܿ݉ଷ ݈ܲܽ‫ ݏݑ݈ݑ݀݋݉ ݊݋݅ݐܿ݁ݏ ܿ݅ݐݏ‬

5) For all beams, values of design yield moment and of design plastic moment are:
‫ܯ‬௬ௗ = ݂௬ௗ ∗ ܹ௘௟ = 43.42 ݇ܰ݉
‫ܯ‬௣ௗ = ݂௬ௗ ∗ ܹ௣௟ = 49.46 ݇ܰ ∗ ݉

2.2

Limit analysis
1) Limit analysis is a method for calculating the ultimate load multiplier which leads to
structural collapse.
2) Limit analysis theorems are:
• Static theorem: λcrit is the highest among those statically admissible.
• Kinematic theorem: λcrit is the minimum of those kinematically compatible.
• Uniqueness theorem: λcrit is the only statically admissible and kinematically
compatible.
3) Thanks to uniqueness theorem, we can consider all kinematically compatible
deformed shapes and find among these the only one statically admissible which is
associated with the ultimate load multiplier λcrit.
4) This procedure allows to not apply separately static theorem and kinematic
theorem to find limit values that identify the range of possibly multipliers.

2.2.1

Kinematic theorem
1) We have to find all kinematically compatible deformed shapes so we consider all
plastic kinematic mechanisms assuming that plastic hinges may be formed in
correspondence of:
• Nodal forces
• Constraints
• Geometric discontinuities
2) System hyperstaticity is 3 so we need 4 plastic hinges to have structural collapse
and this means that there are 6 possible deformed shape depending on where
plastic hinges are positioned.
3) We report possible kinematic mechanisms assuming:
• small displacements
• elastic deformations negligible compared to plastic ones.

Rome, AUGUST 2013

Pag. 11


A.A. 2012/2013

Plastic Behavior

Figure 2.3

4) We apply the thorem of virtual work to every deformed shape assuming that load,
which produced it, is critical one and we write equilibrium equations:
‫ܯ‬௣
ሺ1ሻ + ߣ‫ܯ 4 = ܮ ∗ ߠ ∗ ܪ‬௣ ∗ ߠ → ߣଵ = 5
ܸ∗‫ܮ‬
‫ܯ‬௣
ሺ2ሻ − ߣ‫ܯ 4 = ܮ ∗ ߠ ∗ ܪ‬௣ ∗ ߠ → ߣଶ = −5
ܸ∗‫ܮ‬
10 ‫ܯ‬௣
ሺ3ሻ + ߣ‫ܯ 6 = ܮ ∗ ߠ ∗ ܸߣ + ܮ ∗ ߠ ∗ ܪ‬௣ ∗ ߠ → ߣଷ =
3 ܸ∗‫ܮ‬
‫ܯ‬௣
ሺ4ሻ − ߣ‫ܯ 6 = ܮ ∗ ߠ ∗ ܸߣ + ܮ ∗ ߠ ∗ ܪ‬௣ ∗ ߠ → ߣସ = 30
ܸ∗‫ܮ‬
10 ‫ܯ‬௣
ሺ5ሻ + ߣ‫ܯ 6 = ܮ ∗ ߠ ∗ ܸߣ − ܮ ∗ ߠ ∗ ܪ‬௣ ∗ ߠ → ߣହ = −
3 ܸ∗‫ܮ‬
‫ܯ‬௣
ሺ6ሻ − ߣ‫ܯ 6 = ܮ ∗ ߠ ∗ ܸߣ − ܮ ∗ ߠ ∗ ܪ‬௣ ∗ ߠ → ߣ଺ = −30
ܸ∗‫ܮ‬

2.2.2

Application of uniqueness theorem
1) We take the kinematic mechanism which is associated with the minimum value of
load multiplier in absolute terms and we verify that it is also statically admissible.

Rome, AUGUST 2013

Pag. 12


A.A. 2012/2013

Plastic Behavior
2) To verify this condition, we have to plot evolution of the moment on the structure
considering system labile in collapse step with associated critical loads and we have
to make sure that in every section of the structure moment value is lower than
plastic one.
3) Kinematic mechanisms which are associated with the minimum value of load
multiplier in absolute terms are n.3 and n.5, but only the first verifies static
condition.

Figure 2.4

4) The value of ultimate load multiplier is:
ߣ௖௥ = ߣଷ =

2.3
2.3.1
2.3.1.1

10 ‫ܯ‬௣
54.96 ݇ܰ
=

3 ܸ∗‫ܮ‬
ܸ

Incremental method
SAP2000
Modeling
2) We apply a vertical force P=-1 kN in node E and a horizontal force H=1 kN in node C;
these forces will be used to set push-over analysis, combined so that force H
showing 0.8 times that force V.

Figure 2.5

3) We define a nonlinear static load case called Pushover VH, that uses the base load
patterns P and 80% of H, previously defined. This is a displacement control analysis
in which we monitor node C horizontal displacement.

Rome, AUGUST 2013

Pag. 13


A.A. 2012/2013

Plastic Behavior

Figure 2.6

2.3.1.2

Flexural plastic hinges
1) We have to define properties of flexural plastic hinge in terms of moment-rotation
diagram.
2) We insert values of plastic hinge parameterized curve in the software according to
the following relations (FEMA 356):
• ‫ܯ = ܯ‬௬ → ߠ = 0
•

‫ܯ = ܯ‬௨ → ߠ = ߠ௨ = 4 ߠ௬

• ‫ܯ = ܯ‬௥௘௦ = 0.2 ‫ܯ‬௬ → ߠ = ߠ௙௜௡ = 6 ߠ௬
3) We assign to every beam three plastic hinges: two at the ends and one in the
middle section.

Figure 2.7

Rome, AUGUST 2013

Pag. 14


A.A. 2012/2013
2.3.1.2.1

Plastic Behavior

Results

Figure 2.8
Step
0
1
2
3
4
5
6
7
8
9
10
11
12
13

Displacement
δ (m)
0,00
0,02
0,02
0,04
0,09
0,12
0,15
0,98
0,98
1,01
1,01
1,05
1,05
1,10

Vertical force
V (kN)
0,00
41,71
45,26
49,62
53,27
54,21
53,44
11,61
11,61
9,74
9,74
7,86
7,86
5,21

Horizontal force
H (kN)
0,00
33,37
36,21
39,69
42,62
43,37
42,75
9,29
9,29
7,79
7,79
6,29
6,29
4,17

Figure 2.9


Rome, AUGUST 2013

Pag. 15


A.A. 2012/2013

Plastic Behavior

Figure 2.10

Figure 2.11

Figure 2.12

2) We report the comparison of ultimate load multipliers between the two different
analyzes:
ߣ௖௥,௔௡௔௟௜௧௜௖ = 54.96

→ ‫%83.1 = ݎ݋ݎݎܧ‬
ቐ
ߣ௖௥,௜௡௖௥௘௠௘௡௧௔௟ = 54.21

2.3.1.3

Buckling plastic hinge
1) As we do previously, we have to define values of plastic hinge parameterized curve
in the software:
‫ܯ = ܯ‬௬ → ߠ = 0
‫ܯ = ܯ‬௨ → ߠ = ߠ௨ = 4 ߠ௬
• ܰ = 0 → ቐ
‫ܯ = ܯ‬௥௘௦ = 0.2 ‫ܯ‬௬ → ߠ = ߠ௙௜௡ = 6 ߠ௬

Rome, AUGUST 2013

Pag. 16


A.A. 2012/2013

Plastic Behavior

•

ܰ ≠ 0 = 0,5 ܰ௬ → ቐ

‫ܯ = ܯ‬௥௘௦

‫ܯ = ܯ‬௬ → ߠ = ߠ௬
‫ܯ = ܯ‬௨ → ߠ = ߠ௬
= 0.2 ‫ܯ‬௬ → ߠ = ߠ௙௜௡ = 1.5 ߠ௬

Figure 2.13

2.3.1.3.1

Results
1) As we do previously, we report the results:

Figure 2.14
Step
0
1
2
3
4
5
6
7
8
9
10
11
12

Rome, AUGUST 2013

Displacement
δ (m)
0,00
0,02
0,02
0,04
0,11
0,12
0,14
0,61
0,61
0,63
0,92
0,92
1,10

Vertical force
V (kN)
0,00
46,94
50,98
56,21
61,05
61,04
60,47
29,96
29,96
28,43
16,72
16,72
10,20

Horizontal force
H (kN)
0,00
37,55
40,78
44,97
48,84
48,83
48,37
23,97
23,97
22,74
13,37
13,37
8,16

Pag. 17


A.A. 2012/2013

Plastic Behavior

Figure 2.15

Figure 2.16

Figure 2.17

Figure 2.18

Rome, AUGUST 2013

Pag. 18


A.A. 2012/2013
2.3.1.4

Plastic Behavior

Comparison
1) We report the comparison of pushover curves between the two different analyzes:

Figure 2.19

Pushover curves
70,00
60,00

Multiplier (kN)

50,00
Flexural
hinges

40,00
30,00

Buckling
hinges

20,00
10,00
0,00
0,00

0,20

0,40

0,60

0,80

1,00

1,20

Displacements (m)

Flexural
Buckling

Rome, AUGUST 2013

λcrit (kN)
54,21
61,05

Pag. 19

Exercise n.3: Fixed-ends beam with distributed load

A.A. 2012/2013

Plastic Behavior

EXERCISE N.3

e
FIXED-ENDS BEAM WITH DISTRIBUTED LOAD

3.1

Outline
1) Analytically e numerically find the response in elastic-plastic range of a fixed-ends
beam with distributed load. Numerically investigate sensitivity of solution to
changes in the parameter "length of plastic hinge". Beam structural material is the
one used in exercise n.1

Figure 3.1

Figure 3.2

2) Material data:
• ‫݉݉/ܰ 000012 = ܧ‬ଶ ‫ݏݏ݂݂݁݊݅ݐݏ ܿ݅ݐݏ݈ܽܧ‬
• ݂௬ = 240 ܰ/݉݉ଶ ܻ݈݅݁݀ ‫ݏݏ݁ݎݐݏ‬
•

•

ߝ௬ =

ா
௙೤

= 0,11429 % ܻ݈݅݁݀ ‫݊݅ܽݎݐݏ‬

ߝ௨ = 5 % ܷ݈‫݊݅ܽݎݐݏ ݁ݐܽ݉݅ݐ‬

3) Geometry data:
• ‫ݐ݈݃݊݁ ݉ܽ݁ܤ ݉ 4 = ܮ‬ℎ

• ܾ = 100 ܿ݉ ‫ݐ݀݅ݓ ݈݁݃݊ܽܨ‬ℎ
• ℎ = 200 ܿ݉ ܵ݁ܿ‫݃݅݁ܪ ݊݋݅ݐ‬ℎ‫ ݐ‬
• ‫݉ܿ 5.82 = ܣ‬ଶ ܵ݁ܿ‫ܽ݁ݎܽ ݊݋݅ݐ‬
• ℎ = 200 ܿ݉ ܵ݁ܿ‫݃݅݁ܪ ݊݋݅ݐ‬ℎ‫ ݐ‬
• ‫ݐ‬௙ = 8.5 ݉݉ ‫ݐ ݈݁݃݊ܽܨ‬ℎ݅ܿ݇݊݁‫ ݏݏ‬
•
•
•
•

Rome, AUGUST 2013

‫ݐ‬௪ = 5.6 ݉݉ ܹܾ݁ ‫ݐ‬ℎ݅ܿ݇݊݁‫ ݏݏ‬
‫݉ܿ 0.3491 = ܫ‬ସ ‫ ܽ݅ݐݎ݁݊ܫ‬
ܹ௘௟ = 194.0 ܿ݉ଷ ‫ ݏݑ݈ݑ݀݋݉ ݊݋݅ݐܿ݁ݏ ܿ݅ݐݏ݈ܽܧ‬
ܹ௣௟ = 221.0 ܿ݉ଷ ݈ܲܽ‫ ݏݑ݈ݑ݀݋݉ ݊݋݅ݐܿ݁ݏ ܿ݅ݐݏ‬
Pag. 20


A.A. 2012/2013

Plastic Behavior

‫ܯ‬௬ௗ = ݂௬ௗ ∗ ܹ௘௟ = 46.56 ݇ܰ݉
‫ܯ‬௣ௗ = ݂௬ௗ ∗ ܹ௣௟ = 53.04 ݇ܰ ∗ ݉

3.2

Analytical method
1) Taking as its axis beam axis, starting in A, we denote by v (x) vertical displacement
of generic section along x-axis and by χ (x) its curvature.
3) We make assumption of little displacements, so we can write equilibrium equations
on undeformed shape.

Figure 3.3

3.2.1

Elastic solution
1) We find elastic solution, when, in the first load phase, element stresses are so low
that prevent the passage in plastic range and we derive load λy, which causes first
plastic hinge.

3.2.1.1

Congruence
1) We write congruence equation with boundary conditions:

3.2.1.2

‫ ݒ‬ሺ‫0 = ݔ‬ሻ = 0
݀ ଶ ‫ ݒ‬ሺ‫ݔ‬ሻ
‫ ݒ‬ሺ‫ܮ = ݔ‬ሻ = 0
߯ ሺ‫ݔ‬ሻ =
‫ݐ݅ݓ‬ℎ ൞
‫ ′′ݒ‬ሺ‫0 = ݔ‬ሻ = 0
݀‫ ݔ‬ଶ
‫ ′′ݒ‬ሺ‫ܮ = ݔ‬ሻ = 0



3.2.1.3

Equilibrium

‫ܯ‬ሺ‫ݔ‬ሻ = ‫ ߯ ܫܧ‬ሺ‫ݔ‬ሻ

1) We write the equilibrium equation:

3.2.1.4

Solution

ߣ=

݀ ଶ ‫ܯ‬ሺ‫ݔ‬ሻ
݀‫ ݔ‬ଶ


݀ ସ ‫ ݒ‬ሺ‫ݔ‬ሻ
ߣ
ߣ
= → ‫ݒ‬ሺ‫ݔ‬ሻ = x ସ + Cଷ ∗ x ଷ + Cଶ ∗ x ଶ + Cଵ ∗ x + C଴
ସ
‫ܫܧ‬
‫ܫܧ‬
݀‫ݔ‬

C0,C1,C2 and C3 are constants that we calculate by boundary conditions.

Rome, AUGUST 2013

Pag. 21


A.A. 2012/2013

Plastic Behavior
2) Complete solution is:

‫ݒ‬ሺ‫ݔ‬ሻ =

‫ܯ‬ሺ‫ݔ‬ሻ = −

Figure 3.4

1 ߣ
ሺ‫ݔ − ܮ‬ሻ ‫ݔ‬
24 ‫ܫܧ‬

1
1
1
ߣ‫ܮ‬ଶ + ߣ‫ ݔ ∗ ߣ + ݔ ∗ ܮ‬ଶ
2
2
12

3) First hinges come out simultaneously at the ends when moment in these sections
reaches value of plastic moment:

So when load is:

‫ܯ‬஺ = ‫ܯ‬஻ = ‫ܯ‬௣ = 53,04 ݇ܰ ∗ ݉

ߣ = ߣ௬ =

12
∗ ‫ܯ‬௣ = 39.78 ݇ܰ/݉
‫ܮ‬ଶ

4) At the same time, value of moment in other section is given by following relation:
6
6
6
6
‫ܯ‬ሺ‫ݔ‬ሻ = −‫ܯ‬௣ + ‫ܯ‬௣ ∗ ‫ − ݔ‬ଶ ‫ܯ‬௣ ∗ ‫ ݔ‬ଶ = ‫ܯ‬௣ ଶ ൬−‫ ݔ‬ଶ + ‫ − ݔ ∗ ܮ‬ଶ ൰ < ‫ܯ‬௣
‫ܮ‬
‫ܮ‬
‫ܮ‬
‫ܮ‬

and particularly, value of moment in middle section is:
∗
‫ܯ‬஼

ߣ௬ ∗ ‫ܮ‬ଶ ‫ܯ‬௣
=
=
24
2

5) Evolution of vertical displacement v(x) along x-axis is:

3.2.2

Plastic solution


1 ‫ܯ‬௣
ሺ‫ݔ − ܮ‬ሻ ‫ݔ‬
2 ‫ܮ‬ଶ ‫ܫܧ‬

1) We find plastic solution, or rather we estimate ultimate load λcr, considering that
end sections A and B have already reached plastic range so moment in these
sections can not be higher than plastic moment Mp. This means that beams
behaves as a simply supported beam for next load increments.

Figure 3.5

Rome, AUGUST 2013

Pag. 22


A.A. 2012/2013
3.2.2.1

Plastic Behavior

Congruence
1) We write congruence equation with boundary conditions:

3.2.2.2

߂߯ ሺ‫ݔ‬ሻ =


݀ ଶ ߂‫ ݒ‬ሺ‫ݔ‬ሻ
߂‫ ݒ‬ሺ‫0 = ݔ‬ሻ = 0
‫ݐ݅ݓ‬ℎ ൜
߂‫ ݒ‬ሺ‫ܮ = ݔ‬ሻ = 0
݀‫ ݔ‬ଶ

1) We write constitutive equation:

3.2.2.3

Equilibrium

߂‫ ܯ‬ሺ‫0 = ݔ‬ሻ = 0
߂‫ܯ‬ሺ‫ݔ‬ሻ = ‫ ߯߂ ܫܧ‬ሺ‫ݔ‬ሻ ‫ݐ݅ݓ‬ℎ ൜
߂‫ ܯ‬ሺ‫ܮ = ݔ‬ሻ = 0
݀ ଶ ߂‫ܯ‬ሺ‫ݔ‬ሻ
݀‫ ݔ‬ଶ


3.2.2.4

߂ߣ =

Solution


݀ ସ ߂‫ ݒ‬ሺ‫ݔ‬ሻ ߂ߣ
߂ߣ
=
→ x ସ + Cଷ ∗ x ଷ + Cଶ ∗ x ଶ + Cଵ ∗ x + C଴
ସ
‫ܫܧ‬
‫ܫܧ‬
݀‫ݔ‬

C0,C1,C2 and C3 are constants that we calculate by boundary conditions.
2) Complete solution is:
߂‫ݒ‬ሺ‫ݔ‬ሻ =

1 ߂ߣ
ሺ‫ݔ − ܮ‬ሻ(‫ܮ‬ଶ − ‫ ݔ + ݔܮ‬ଶ ) ‫ݔ‬
24 ‫ܫܧ‬

1
1
߂‫ܯ‬ሺ‫ݔ‬ሻ = ߂ߣ‫ ݔ ∗ ߣ߂ + ݔ ∗ ܮ‬ଶ
2
2

Figure 3.6

3) Next plastic hinge comes out in middle section C, when moment reaches plastic
value:

∗
‫ܯ‬௖ = ‫ܯ‬஼ + ߂‫ܯ‬௖ =

‫ܯ‬௣
+ ߂‫ܯ‬௖ = ‫ܯ‬௣ = 53.04 ݇ܰ ∗ ݉
2

‫ܯ‬௣
4
→ ߂ ߣ = ଶ ∗ ‫ܯ‬௣ = 39.78 ݇ܰ/݉
‫ܮ‬
2
16
ߣ = ߣ௣ = ߣ௬ + ߂ ߣ = ଶ ∗ ‫ܯ‬௣ = 53.04 ݇ܰ/݉
‫ܮ‬
6) At the same time, value of moment in other sections is:
So when load is:

߂‫ܯ‬௖ =

‫ܯ‬ሺ‫ݔ‬ሻ = ‫ܯ‬௣ ൬−1 +
Rome, AUGUST 2013

8
8
∗ ‫ ݔ‬ଶ + ∗ ‫ ݔ‬൰ < ‫ܯ‬௣
ଶ
‫ܮ‬
‫ܮ‬
Pag. 23


A.A. 2012/2013

Plastic Behavior
and evolution of vertical displacement v(x):

1 ‫ܯ‬௣
ሺ−‫ ݔ‬ସ + ‫ ݔ ∗ ܮ‬ଷ − ሺ‫ܮ‬ଶ + ‫3 + ܮ‬ሻ ∗ ‫ ܮ + ݔ‬ሺ‫ܮ‬ଶ + 3ሻ ∗ ‫ݔ‬ሻ
6 ‫ܮ‬ଶ ‫ܫܧ‬

7) We can evaluate structure overstrength in terms of load λ

ߣ௣ 4
= → ܱ‫ݐ݃݊݁ݎݐݏݎ݁ݒ‬ℎ = +33.3%
ߣ௬ 3

3.2.3

Length of plastic hinge
1) Analytical method is not strictly correct because, when moment reach yield value in
end sections A and B:
‫ܯ‬௬ = 46,56 ݇ܰ ݉ → ߣଵ =

12
‫ ݉/ܰ݇ 29,43 = ܯ‬
‫ܮ‬ଶ ௬

entire section don't reach a the same time plastic range, but gradually from outer to
inner parts until the formation of plastic hinge. During this step, section behaviour
is not elastic, as we assumed, but more complex and not easy to model with a
simple equation.
2) When moment increases, also, near sections exceed yield limit so, when in A e B
moment reaches plastic value Mp=53.04 kN m, close sections, at both beam ends,
are partially in plastic range.
3) This means that plastic hinge is not punctual but has a length L*1,i, that we can
calculate considering the evolution of moment along beam during elastic step:
‫ܯ‬ሺ‫ݔ‬ሻ = ‫ܯ‬௣

6
6
൬−‫ ݔ‬ଶ + ‫ − ݔ ∗ ܮ‬ଶ ൰
ଶ
‫ܮ‬
‫ܮ‬

We can calculate value of x for which M=My

‫ܮ‬
1
1
‫ = ∗ܮ‬ቌ1 − ඨ1 − ൬‫ + ܮ‬൰ቍ = 7.02 ܿ݉
ଵ,௜
4
36
ߚ

೛
with ߚ = Section shape factor = ெ =

ெ

೤

ௐ೛೗
ௐ೐೗

= 1.1392

4) We have the same situation in section C when load increases till critical value: when
middle section is completely in plastic range, those near have partially overcome
yield strength so we have to calculate plastic hinge length.

Figure 3.7

Rome, AUGUST 2013

Pag. 24


A.A. 2012/2013

Plastic Behavior
1) We can calculate final lengths L*1 and L*2 considering evolution of moment during
plastic step:
‫ܯ‬ሺ‫ݔ‬ሻ = ‫ܯ‬௣ ൬−1 +

8
8
∗ ‫ ݔ‬ଶ + ∗ ‫ ݔ‬൰
‫ܮ‬ଶ
‫ܮ‬

2) We can estimate length L*1 setting M(x)=-My:

1
‫ܮ‬
1
‫ = ∗ܮ‬ቌ1 − ඨ ൬1 + ൰ቍ = 6.20 ܿ݉
ଵ
2
2
ߚ
3) We make a change of coordinate to calculate length L*2 setting origin in the middle
section:
2
‫ܮ‬
ߦ = ‫ = ݔ → ݔ‬ሺߦ + 1ሻ
‫ܮ‬
2
Previous relation of moment becomes:

‫ܯ‬ሺߦሻ = ‫ܯ‬௣ ሺ−1 + 4ሺߦ + 1ሻ − 2ሺߦ + 1ሻଶ ሻ

4) Setting M(ߦ)=-My, we estimate ߦ*2, then L*2:
∗
ߦଶ =

3.3
3.3.1
3.3.1.1

ඨ

1−
2

1
ߚ

∗
→ ‫ = ∗ܮ‬ሺߦଶ + 1ሻ‫݉ܿ 69,89 = ܮ‬
ଶ

Incremental method
SAP2000
Modeling
1) The structure is modeled by 2 frame elements with material and section properties
previously indicated. Structure ends are fixed with restraints
2) We apply a vertical distributed load q=-1 kN/m, that will be used to set push-over
analysis.
3) We have to define properties of flexural plastic hinge in terms of moment-curvature
diagram, so we have to calculate yield curvature χy and collapse curvature χu:
߯௬ =

ߝ௬
= 1,14286 % ܻ݈݅݁݀ ܿ‫݁ݎݑݐܽݒݎݑ‬
ℎ
2

߯௨ =

Rome, AUGUST 2013

ߝ௨
= 50 % ‫݁ݎݑݐܽݒݎݑܿ ݁ݏ݌݈݈ܽ݋ܥ‬
ℎ
2

Pag. 25


A.A. 2012/2013

Plastic Behavior

Figure 3.8

3.3.1.2

Analysis
1) We produce 10 different models of this type, by varying relative length of plastic
hinge from a value of 0.01 (4 cm) to a value of 1 (4 m, total length of beam). Also we
define another model using plastic hinges with lengths calculated previously in
analytical method, so 6,20 cm for end sections and 98,96 cm for middle one.
2) For each model, we assign its own plastic hinge by positioning three ones: two in
ends and one in middle section.
3) We define a nonlinear static load case called Pushover q, that uses the base load
patterns q, previously defined. This is a displacement control analysis in which we
monitor vertical displacement of middle joint.

Figure 3.9

Rome, AUGUST 2013

Pag. 26


A.A. 2012/2013
3.3.1.3

Plastic Behavior

Results
1) We report the results of analysis on all models:
Lp= 0,010 = 4 cm

Lp= 0,100 = 40 cm

Step

λ (kN)

δ (mm)

λ (kN)

δ (mm)

λ (kN)

δ (mm)

λ (kN)

δ (mm)

0,00

0,00

0,00

0,00

0,00

0,00

0,00

0,00

34,92

6,48

34,92

6,48

34,92

6,48

34,92

6,48

2

48,79

15,93

47,51

16,11

47,04

16,18

46,80

16,21

3

50,56

22,26

51,93

51,56

52,40

101,21

52,66

200,84

4

50,56

22,26

51,93

51,56

52,40

101,21

52,66

200,84

5

51,84

38,48

51,93

51,56

52,40

101,21

52,66

200,84

6

51,84

38,48

52,04

68,48

52,06

118,36

52,08

218,12

7

51,84

38,48

52,04

68,48

52,06

118,36

52,08

218,12

8

-0,29

539,82

52,04

68,48

52,06

118,36

52,08

218,12

9

Figure 3.12

Lp= 0,050 = 20 cm

1

Figure 3.11

Lp= 0,025 = 10 cm

0

Figure 3.10

0,00

0,00

-0,09

569,81

-0,06

619,70

-0,05

719,45

Lp= 0,200 = 80 cm Lp= 0,300 = 120 cm Lp= 0,400 = 160 cm Lp= 0,500 = 200 cm
Step λ (kN) δ (mm) λ (kN)
δ (mm)
λ (kN)
δ (mm)
λ (kN)
δ (mm)
0
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
1
34,92
6,48
34,92
6,48
34,92
6,48
34,92
6,48
2
46,68
16,23
46,64
16,23
46,62
16,24
46,61
16,24
3
52,79
400,28
52,83
599,76
52,85
799,25
52,86
998,74
4
52,79
400,28
52,83
599,76
52,85
799,25
52,86
998,74
5
52,79
400,28
52,83
599,76
52,85
799,25
52,86
998,74
6
52,09
417,62
52,09
617,12
52,09
816,62
52,09
1016,12
7
52,09
417,62
52,09
617,12
52,09
816,62
52,09
1016,12
8
52,09
417,62
52,09
617,12
52,09
816,62
52,09
1016,12
9
-0,04
918,96
12,28
1000,00
33,02
1000,00
1,78
1500,00
Lp= 0,750 = 300 cm Lp= 1,000 = 400 cm
Step λ (kN)
δ (mm)
λ (kN)
δ (mm)
0
0,00
0,00
0,00
0,00
1
34,92
6,48
34,92
6,48
2
46,59
16,24
46,58
16,24
3
52,38 1497,64 52,39 1996,39
4
52,38 1497,64 52,39 1996,39
5
52,38 1497,64 52,39 1996,39
6
51,60 1514,71 52,39 1996,39
7
51,60 1514,71
0,29
2497,75
8
51,60 1514,71
9
-0,52
2016,04

Rome, AUGUST 2013

Step
0
1
2
3
….
6
….
9
….
20
….
28

Lp from analytical method
λ (kN)
δ (mm)
0,00
0,00
34,92
6,48
47,33
16,14
49,85
64,47
….
….
29,68
515,02
….
….
23,89
570,68
….
….
22,52
590,19
….
….
21,84
609,51
Pag. 27


A.A. 2012/2013

Plastic Behavior

Figure 3.13

P (kN)

Pushover curves

60,00
55,00
50,00
45,00
40,00
35,00
30,00
25,00
20,00
15,00
10,00
5,00
0,00
0,00

400,00

800,00

1200,00

1600,00

2000,00

2400,00

δ (mm)
Analytical method

Lp = 0.010

Lp = 0.025

Lp = 0.050

Lp = 0.100

Lp = 0.200

Lp = 0.300

Lp = 0.400

Lp = 0.500

Lp = 0.750

Lp = 1.000

Lp from analytical method

2) When length of plastic hinges increases, first, load multiplier switches from minimal
value λ=51,84 kN/m for Lp=0.010 to the highest λ=52,39 kN/m for Lp=0.500; after,
it slightly decreases till λ=52,39 kN/m for Lp=1.000.
3) When length of plastic hinges increases, beam stiffness decreases after formation
of first plastic hinges at the ends, so critical value of load multiplier is reached for
increasing displacements. This means that ductility of system increases.
4) We assume, as ultimate load multiplier, the one that comes out from model with
length of plastic hinges calculated in analytical method.
ߣ௖௥ = 49,85 ݇ܰ/݉
→ ‫% 04,6 = ݎ݋ݎݎܧ‬
ߣ௖௥,௔௡.௠௘௧௛௢ௗ = 53,04 ݇ܰ/݉

Rome, AUGUST 2013

Pag. 28


A.A. 2012/2013

Plastic Behavior

Figure 3.14

Figure 3.15

Rome, AUGUST 2013

Pag. 29

Exercise n.4: Plane structure with two floors

A.A. 2012/2013

Plastic Behavior

EXERCISE N.4

PLANE STRUCTURE WITH TWO FLOORS

4.1

Outline
1) Evaluate first yielding load multiplier and the ultimate one with pushover analysis,
considering flexural plastic hinges Add, next, buckling to plastic hinges and compare
the results

Figure 4.1

Figure 4.2

2) Material data:
• ‫݉݉/ܰ 000012 = ܧ‬ଶ ‫ݏݏ݂݂݁݊݅ݐݏ ܿ݅ݐݏ݈ܽܧ‬
• ݂௬௞ = 235 ܰ/݉݉ଶ ܻ݈݅݁݀ ‫ݏݏ݁ݎݐݏ‬
•

•
•

Rome, AUGUST 2013

݂௬ௗ =

ߝ௬ௗ =

௙೤ೖ

ఊಾబ
௙೤೏

= 223.81 ܰ/݉݉ଶ ‫ݏݏ݁ݎݐݏ ݈݀݁݅ݕ ݊݃݅ݏ݁ܦ‬

= 0,10658 % ‫݊݅ܽݎݐݏ ݈݀݁݅ݕ ݊݃݅ݏ݁ܦ‬

ߝ௨ = 5 % ܷ݈‫݊݅ܽݎݐݏ ݁ݐܽ݉݅ݐ‬
ா

Pag. 30


A.A. 2012/2013

Plastic Behavior
3) Geometry data:
• ‫ݐ݈݃݊݁ ݉ܽ݁ܤ ݉ 4 = ܮ‬ℎ
• ܾ = 100 ܿ݉ ‫ݐ݀݅ݓ ݈݁݃݊ܽܨ‬ℎ
• ℎ = 200 ܿ݉ ܵ݁ܿ‫݃݅݁ܪ ݊݋݅ݐ‬ℎ‫ ݐ‬
• ‫݉ܿ 5.82 = ܣ‬ଶ ܵ݁ܿ‫ܽ݁ݎܽ ݊݋݅ݐ‬
• ℎ = 200 ܿ݉ ܵ݁ܿ‫݃݅݁ܪ ݊݋݅ݐ‬ℎ‫ ݐ‬
• ‫ݐ‬௙ = 8.5 ݉݉ ‫ݐ ݈݁݃݊ܽܨ‬ℎ݅ܿ݇݊݁‫ ݏݏ‬
•
•
•
•

‫ݐ‬௪ = 5.6 ݉݉ ܹܾ݁ ‫ݐ‬ℎ݅ܿ݇݊݁‫ ݏݏ‬
‫݉ܿ 0.3491 = ܫ‬ସ ‫ ܽ݅ݐݎ݁݊ܫ‬
ܹ௘௟ = 194.0 ܿ݉ଷ ‫ ݏݑ݈ݑ݀݋݉ ݊݋݅ݐܿ݁ݏ ܿ݅ݐݏ݈ܽܧ‬
ܹ௣௟ = 221.0 ܿ݉ଷ ݈ܲܽ‫ ݏݑ݈ݑ݀݋݉ ݊݋݅ݐܿ݁ݏ ܿ݅ݐݏ‬


4.2
4.2.1
4.2.1.1

Incremental method
SAP2000
Modeling

‫ܯ‬௬ௗ = ݂௬ௗ ∗ ܹ௘௟ = 43.42 ݇ܰ݉
‫ܯ‬௣ௗ = ݂௬ௗ ∗ ܹ௣௟ = 49.46 ݇ܰ ∗ ݉

2) We apply vertical forces P=-1 kN and horizontal forces H=1 k, as indicated in figure
4.1; these forces will be used to set push-over analysis, combined so that force H
showing 0.25 times that force V.

Figure 4.3

3) We define a nonlinear static load case called Pushover VH, that uses the base load
patterns P and 25% of H, previously defined. This is a displacement control analysis
in which we monitor node 9 (top left) horizontal displacement.
Rome, AUGUST 2013

Pag. 31


A.A. 2012/2013

Plastic Behavior

Figure 4.4

4.2.1.2

Flexural plastic hinges
1) We have to define properties of flexural plastic hinge in terms of moment-rotation
diagram.
2) We insert values of plastic hinge parameterized curve in the software according to
the following relations (FEMA 356):
• ‫ܯ = ܯ‬௬ → ߠ = 0
•

‫ܯ = ܯ‬௨ → ߠ = ߠ௨ = 4 ߠ௬

• ‫ܯ = ܯ‬௥௘௦ = 0.2 ‫ܯ‬௬ → ߠ = ߠ௙௜௡ = 6 ߠ௬
3) We assign to every beam three plastic hinges: two at the ends and one in the
middle section.

Rome, AUGUST 2013

Pag. 32


A.A. 2012/2013
4.2.1.2.1

Plastic Behavior

Results

Figure 4.5

Displacement Vertical force Horizontal force
Step
δ (m)
V (kN)
H (kN)
0
0,00
0,00
0,00
1
0,04
255,02
21,25
2
0,08
363,39
30,28
3
0,08
366,34
30,53
4
0,09
377,02
31,42
5
0,10
379,13
31,59
6
0,16
394,11
32,84
7
0,32
400,94
33,41
8
0,37
396,83
33,07
…
…
…
…
11
0,86
283,77
23,65
…
…
…
…
17
1,77
130,12
10,84
…
…
…
…
19
1,86
116,65
9,72
…
…
…
…
25
2,62
50,27
4,19
…
…
…
…
30
3,51
14,91
1,24

Figure 4.6

Rome, AUGUST 2013

Pag. 33


A.A. 2012/2013

Plastic Behavior

Figure 4.7

Pushover curve

Figure 4.8
450,00
400,00

Critical Load
λ=400,94 kN

350,00

Multiplier (kN)

300,00
250,00

First Yielding
λ=255,02 kN

200,00

Overstrength
1,57

150,00
100,00
50,00
0,00
0,00

0,10

0,20

0,30

0,40

0,50

Displacements (m)


Rome, AUGUST 2013

Pag. 34


A.A. 2012/2013

Plastic Behavior

Figure 4.9

Figure 4.10

Figure 4.11

Figure 4.12

Figure 4.13

Rome, AUGUST 2013

Pag. 35


A.A. 2012/2013
4.2.1.3

Plastic Behavior

Buckling plastic hinge
1) As we do previously, we have to define values of plastic hinge parameterized curve
in the software:
‫ܯ = ܯ‬௬ → ߠ = 0
‫ܯ = ܯ‬௨ → ߠ = ߠ௨ = 4 ߠ௬
• ܰ = 0 → ቐ
‫ܯ = ܯ‬௥௘௦ = 0.2 ‫ܯ‬௬ → ߠ = ߠ௙௜௡ = 6 ߠ௬
•

ܰ ≠ 0 = 0,5 ܰ௬ → ቐ
‫ܯ = ܯ‬௥௘௦

‫ܯ = ܯ‬௬ → ߠ = ߠ௬
‫ܯ = ܯ‬௨ → ߠ = ߠ௬
= 0.2 ‫ܯ‬௬ → ߠ = ߠ௙௜௡ = 1.5 ߠ௬

Figure 4.13

Figure 4.14

Rome, AUGUST 2013

Pag. 36


A.A. 2012/2013
4.2.1.3.1

Plastic Behavior

Results
1) As we do previously, we report the results:

Figure 4.15

Displacement Vertical force Horizontal force
Step
δ (m)
V (kN)
H (kN)
0
0,00
0,00
0,00
1
0,03
182,85
15,24
2
0,04
210,20
17,52
3
0,07
224,50
18,71
4
0,14
231,03
19,25
5
0,17
232,69
19,39
6
0,37
228,83
19,07
7
0,57
224,94
18,75
…
…
…
…
48
8,57
74,10
6,18
…
…
…
…
50
8,57
74,10
6,18

Figure 4.16

Rome, AUGUST 2013

Pag. 37


A.A. 2012/2013

Plastic Behavior

Figure 4.17

Pushover curve

Figure 4.18
250,00

Critical Load
λ=232,69kN

Multiplier (kN

200,00
First Yielding
λ=182,85 kN

150,00

Overstrength
1,27
100,00

50,00

0,00
0,00

0,10

0,20

0,30

0,40

0,50

Displacements (m)


Rome, AUGUST 2013

Pag. 38


A.A. 2012/2013

Plastic Behavior

Figure 4.19

Figure 4.20

Figure 4.21

Figure 4.22

Rome, AUGUST 2013

Pag. 39


A.A. 2012/2013
4.2.1.4

Plastic Behavior

Comparison
1) We report the comparison of pushover curves between the two different analyzes:

Figure 4.23

Pushover curves
450,00
400,00
350,00
300,00

M3 Hinge

Multiplier

250,00

P-M3 Hinge

200,00
150,00
100,00
50,00
0,00
-50,00
-1,00

1,00

Figure 4.24

3,00
5,00
Displacements (m)

7,00

9,00

Pushover curves
450,00
400,00
350,00

Multiplier

300,00
250,00

M3 Hinge

200,00

P-M3 Hinge

150,00

First Yielding
Critical load

100,00
50,00
0,00
-50,00

0,00

0,10

0,20

0,30

0,40

0,50

Displacements (m)

Rome, AUGUST 2013

Pag. 40

Exercise n.4: Plane structure with t
two floors

A.A. 2012/2013

Plastic Behavior

Figure 4.25

Load Multiplier
500,00

Critical load
+41,96 %

450,00
400,00
350,00

M3 Hinge

First Yielding
+28,30 %

300,00

P-M3 Hinge

250,00
200,00
150,00
100,00
50,00
0,00

Figure 4.26

Displacements
0,40

Critical load
+46,70 %

0,35
0,30
0,25

M3 Hinge

0,20
P-M3 Hinge
0,15
0,10

First Yielding
+28,30 %

0,05
0,00

Overstrength

Figure 4.27

Du
uctility
8

1,8

+19,05 %

1,6
1,4

6

1,2

5

1

4

0,8

3

0,6

2

0,4

1

0,2

0

0
M3 Hinge
3

Rome, AUGUST 2013

+25,67 %

7

P-M3 Hinge

M3 Hing
ge

P-M3 Hinge

Pag. 41

Exercise n.5: Critical and post-critical behavior of a bounded beam with concentrated load

A.A. 2012/2013

Buckling

EXERCISE N.5

e
CRITICAL AND POST-CRITICAL BEHAVIOR OF A BOUNDED BEAM WITH
CONCENTRATED LOAD

5.1

Outline
1) Analyze the behavior of an axially loaded beam with three different boundary
conditions, in order to highlight post-critical behavior: stable (case a), unstable
(case b) and asymmetric (case c). Study the system analytically and compare results
with those obtained by using a computational code. For each of three cases,
conduct analysis considering first ideal beam, then real beam with geometric
imperfections: in particular, consider three different rotations that produce
displacement on the top equal to 0,1l, 0,2l and 0,3l.

Figure 5.1

a)

b)

c)

2) Geometry data:
• ‫ݐ݈݃݊݁ ݉ܽ݁ܤ ݉ 1 = ܮ‬ℎ
•

5.2
5.2.1

݇ = 1

௞ே
ܵ‫ݏݏ݂݂݁݊݅ݐݏ ݃݊݅ݎ݌‬
௠

Case A
Analytical method
1) We apply the static approach to solve problem, so we write equilibrium equation
on deformed shape and we obtain critical load multiplier as the one that nullify
geometric stiffness of system.
2) We assume rotation θ as free degree of freedom. In analysis with real beam, its
geometric imperfection is modeled by another starting rotation θ0, that reduce
displacement and value of critical load multiplier.

Figure 5.2

Rome, AUGUST 2013

Pag. 41


A.A. 2012/2013
5.2.1.1
5.2.1.1.1

Buckling

Ideal beam
Small displacements
1) We obtain geometric stiffness of system k* writing equilibrium equation in
deformed shape:
݇ ∗ ߠ = ܲ ∗ ݈ ∗ ߠ → ሺ݇ − ܲ ∗ ݈ሻ ∗ ߠ = 0 → ݇ ∗ = (݇ − ܲ ∗ ݈)
2) The value of load P that nullify this stiffness is the critical one:

5.2.1.1.2

݇
ܲ௖௥ ∗ ݈
=1
ܲ௖௥ = →
݈
݇

Large displacements

deformed shape:
݇ ∗ ߠ = ܲ ∗ ݈ ∗ sin ߠ → ൬݇ − ܲ ∗ ݈ ∗

sin ߠ
sin ߠ
൰ ∗ ߠ = 0 → ݇ ∗ = (݇ − ܲ ∗ ݈ ∗
)
ߠ
ߠ


5.2.1.2
5.2.1.2.1

Real beam
Small displacements

݇ sin ߠ
ܲ௖௥ ∗ ݈
ߠ
ܲ௖௥ =
→
=
݇
݈ ߠ
sin ߠ

deformed shape:
݇ ∗ ሺߠ − ߠ଴ ሻ = ܲ ∗ ݈ ∗ ߠ → ݇ ∗ ߠ ∗ ൬1 −
݇ ∗ = ݇ ∗ ൬1 −

ܲ ∗ ݈ ߠ଴
− ൰ = ݇∗ ∗ ߠ = 0
݇
ߠ

ܲ ∗ ݈ ߠ଴
− ൰
ߠ
݇

ܲ௖௥ =

5.2.1.2.2

Large displacements

݇
ߠ଴
ܲ௖௥ ∗ ݈
ߠ଴
൬1 − ൰ →
= ൬1 − ൰
݈
݇
ߠ
ߠ

deformed shape:
݇ ∗ ሺߠ − ߠ଴ ሻ = ܲ ∗ ݈ ∗ sin ߠ → ݇ ∗ ൬1 −
݇ ∗ = ݇ ∗ ൬1 −

Rome, AUGUST 2013

ܲ ∗ ݈ sin ߠ ߠ଴
∗
− ൰ = ݇∗ ∗ ߠ = 0
ߠ
݇
ߠ

ܲ ∗ ݈ sin ߠ ߠ଴
∗
− ൰
݇
ߠ
ߠ

Pag. 42


A.A. 2012/2013

Buckling

5.2.1.3

݇ ߠ − ߠ଴
ܲ௖௥ ∗ ݈ ߠ − ߠ଴
ܲ௖௥ =
→
=
ߠ
ߠ
݈
݇

Results

2) We report the evolution of critical load at varying of angle θ for all considered
situations:

Critical load

Figure 5.3

1,50

PL/k

I.B. - L.D.
1,25
R.B. - L.D.
1,00
I.B. - S.D.
0,75
R.B. - S.D.
0,50
0,25

-90,000

-60,000
I.B.- S.D.
R.B.- S.D.- 0.3

-30,000

0,00
0,000
θ (°)

I.B. - L.D.
R.B.- L.D.- 0.1

30,000
R.B.- S.D.- 0.1
R.B.- L.D.- 0.2

60,000

90,000
R.B.- S.D.- 0.2
R.B.- L.D.- 0.3

3) In all situations, when angle θ increases, critical load becomes higher and this
means that post-critical behavior is stable.
4) When we consider real beam, at increasing of angle θ0, that models geometric
imperfection of system, critical load always results smaller.

5.2.2
5.2.2.1
5.2.2.1.1
5.2.2.1.1.1

Incremental method
Real beam
SAP2000
Modeling
1) The structure is modeled by a beam element to which we assign fictitious material
and section with high stiffness to keep strain low.
2) We made three models with a different value of starting rotation to model
geometric imperfection (θ0=0,1l, θ0=0,2l and θ0=0,3l).
3) We assign a rotational spring to the bottom end of beam and an axial load P to the
top, that will be used to set pushover analysis.
4) We define two nonlinear static load cases called P-SD and P-LD, that both use the
base load pattern P, previously defined. Pushover-SNG case considers only

Rome, AUGUST 2013

Pag. 43


A.A. 2012/2013

Buckling
geometric nonlinearity parameter P-Delta (it coincides with previous small
displacement analysis) whereas Pushover-SG case considers both P-delta and large
displacements.

Figure 5.4

5.2.2.1.1.2

Results
1) We report results of incremental analysis compared with those ones by previous
analytical method:

Small displacements - θ = 0,1 L

Figure 5.5

1,50

PL/k

1,25
1,00
0,75
0,50
0,25

-90,000

-60,000
Analytical

Rome, AUGUST 2013

-30,000

0,00
0,000
θ (°)

SAP - Tolerance=0.01

30,000

60,000

90,000

SAP - Tolerance=0,0001

Pag. 44


A.A. 2012/2013

Buckling


Figure 5.6

PL/k

1,50
1,25
1,00
0,75
0,50
0,25

-90,000

-60,000

-30,000

0,00
0,000

30,000

60,000

90,000

θ (°)
Analytical

SAP - Tolerance 0.1


Figure 5.7

PL/k

1,50
1,25
1,00
0,75
0,50
0,25

-90,000

-60,000

-30,000

0,00
0,000

30,000

60,000

90,000

θ (°)
Analytical

Rome, AUGUST 2013

SAP - Tolerance=0.1


Pag. 45


A.A. 2012/2013

Buckling

Figure 5.8

Large displacements
PL/k

1,50
1,25
1,00
0,75
0,50
0,25

-90,000

-60,000

-30,000

0,00
0,000

30,000

60,000

90,000

θ (°)
θ=0,1L

5.3
5.3.1

θ=0,2L

θ=0,3L

θ=0,1L - SAP

θ=0,2L - SAP

θ=0,3L - SAP

Case B
Analytical method

Figure 5.9

5.3.1.1
5.3.1.1.1

Ideal beam
Small displacements
deformed shape:
݇ ∗ ݈ ଶ ∗ ߠ = ܲ ∗ ݈ ∗ ߠ → ሺ݇ ∗ ݈ − ܲሻ ∗ ߠ = ݇ ∗ ∗ ߠ = 0 → ݇ ∗ = (݇ ∗ ݈ − ܲ)
ܲ௖௥ = ݇ ∗ ݈ →

Rome, AUGUST 2013

ܲ௖௥
=1
݇∗݈
Pag. 46


A.A. 2012/2013
5.3.1.1.2

Buckling

Large displacements
deformed shape:
݇ ∗ ݈ cos ߠ − ܲ
݇ ∗ ݈ ଶ ∗ sin ߠ cos ߠ = ܲ ∗ ݈ ∗ sin ߠ → ൬
൰ ∗ ߠ = ݇ ∗ ∗ ߠ = 0
ߠ
݇∗ = ൬

݇ ∗ ݈ cos ߠ − ܲ
൰
ߠ

ܲ௖௥ = ݇ ∗ ݈ cos ߠ →

5.3.1.2
5.3.1.2.1

Real beam
Small displacements

ܲ௖௥
= cos ߠ
݇∗݈

deformed shape:
݇ ∗ ݈ ଶ ሺߠ − ߠ଴ ሻ = ܲ ∗ ݈ ∗ ߠ → ݇ ∗ ݈ ∗ ൬1 −
݇ ∗ = ݇ ∗ ݈ ∗ ൬1 −

ߠ଴
ܲ
− ൰ ∗ ߠ = ݇∗ ∗ ߠ = 0
݇∗݈ ߠ

ܲ
ߠ଴
− ൰
݇∗݈ ߠ

ܲ௖௥ = ݇ ∗ ݈ ൬1 −

5.3.1.2.2

ߠ଴
ܲ௖௥
ߠ଴
൰ →
= ൬1 − ൰
ߠ
݇∗݈
ߠ

Large displacements
deformed shape:
݇ ∗ ݈ ଶ ሺsin ߠ − sin ߠ଴ ሻ ∗ cos ߠ = ܲ ∗ ݈ ∗ sin ߠ

ሺsin ߠ − sin ߠ଴ ሻ ∗ cos ߠ
ܲ
−
݇ ∗ ݈ ∗ ቆ
ቇ ∗ ߠ = ݇∗ ∗ ߠ = 0
݇∗݈∗ߠ
ߠ ∗ sin ߠ

ሺsin ߠ − sin ߠ଴ ሻ ∗ cos ߠ ܲ
݇ ∗ = ݇ ∗ ݈ ቆ
− ቇ
ߠ ∗ sin ߠ
ߠ

ܲ௖௥
ܲ௖௥ = ݇ ∗ ݈ ቆ
=
ቇ →
sin ߠ
sin ߠ
݇∗݈

.
Rome, AUGUST 2013

Pag. 47


A.A. 2012/2013
5.3.1.3

Buckling

Results
situations:

Critical load

Figure 5.10

P/(kL)
I.B. - S. D
1,00
I.B. - L.D.
0,75

R.B. - S.D

0,50
0,25

-90,000

-60,000

-30,000

R.B. - L.D.

0,00
0,000

30,000

60,000

90,000

-0,25
-0,50
θ (°)
I.B. - S.D.
R.B. - S.D. - 0.2

I.B. - L.D.
R.B. - S.D. - 0.3

R.B. - S.D. - 0.1
R.B. - L.D. - 0.1

imperfection of system, critical load always results smaller.
3) In all situations of large displacements, when angle θ increases, critical load
becomes lower, so post-critical behavior is unstable. This happens because spring
reaction always pushes down beam at increasing of angle θ and, when it exceeds
90°, reaction makes an unfavorable contribution to stability. This condition is not
observable in conditions of small displacements because, by assumption, spring
does not change its position and stays at a distance l from bottom restraint of
beam.

5.3.2
5.3.2.1
5.3.2.1.1
5.3.2.1.1.1

Incremental method
Real beam
SAP2000
Modeling
1) We use same models previously described in case A, only with addition of a
translational spring on the top of the beam.

5.3.2.1.1.2

Results
analytical method:

Rome, AUGUST 2013

Pag. 48


A.A. 2012/2013

Buckling

Figure 5.11

1,500

PL/k

1,250
1,000
0,750
0,500
0,250

-90,000

-60,000
Analytical

-30,000

0,000
0,000
θ (°)

30,000


60,000

90,000


Figure 5.12

1,500

PL/k

1,250
1,000
0,750
0,500
0,250

-90,000

-60,000

-30,000

0,000
0,000

30,000

60,000

90,000

θ (°)
Analytical

Rome, AUGUST 2013

SAP - Tolerance=0,1


Pag. 49


A.A. 2012/2013

Buckling

Figure 5.13

PL/k
1,250
1,000
0,750
0,500
0,250

-90,000

-60,000
Analytical

-30,000

0,000
0,000
θ (°)

30,000

SAP - Tolerance=0,1

60,000

90,000


Large displacements
Figure 5.14
1,000

PL/k

0,750

0,500

0,250

-90,000

-60,000
θ=0,1L
θ=0,1L - SAP

5.4
5.4.1

0,000
-30,000
0,000
θ (°)
θ=0,2L

30,000

D - 0.2L - SAP

60,000

90,000

θ=0,3L
θ=0,3L - SAP

Case C
Analytical method

Rome, AUGUST 2013

Pag. 50


A.A. 2012/2013

Buckling

Figure 5.14

3) We denote by α angle that spring makes with horizontal axis on deformed shape:
ߨ ߠ
ߙ= −
4 2
4) Elongation of spring:

݀ = ݈ ∗ √2 ∗ ൫ඥ1 + sin ߠ − sin ߠ଴ − 1൯
This expression is obtained on assumptions of large displacements and beam with
geometric imperfection, but it can be used also in other situation setting:
•
•

5.4.1.1
5.4.1.1.1

‫ߠ ݊݅ݏ − ߠ ݊݅ݏ‬଴ = ߠ − ߠ଴ ݈݈ܵ݉ܽ ݀݅‫ݏݐ݈݊݁݉݁ܿܽ݌ݏ‬
ߠ଴ = 0 ‫ܾ݉ܽ݁ ݈ܽ݁݀ܫ‬

Ideal beam
Small displacements
deformed shape:
݇ ∗ ݈ ଶ ∗ ൫√1 + ߠ − 1൯ ∗ ሺ1 − ߠሻ = ܲ ∗ ݈ ∗ ߠ

ܲ
൫√1 + ߠ − 1൯ ∗ ሺ1 − ߠሻ
݇ ∗ ݈ ∗ ቆ
−
ቇ ∗ ߠ = ݇ ∗ ∗ ߠ = 0
݇∗݈
ߠ
ܲ
൫√1 + ߠ − 1൯ ∗ ሺ1 − ߠሻ
݇ ∗ = ݇ ∗ ݈ ∗ ቆ
−
ቇ
݇∗݈
ߠ

ܲ௖௥ = ݇ ∗ ݈ ∗

5.4.1.1.2

ܲ௖௥
൫√1 + ߠ − 1൯ ∗ ሺ1 − ߠሻ
൫√1 + ߠ − 1൯ ∗ ሺ1 − ߠሻ
→
=
ߠ
ߠ
݇∗݈

Large displacements
deformed shape:
ߨ ߠ
ߨ ߠ
݇ ∗ ݈ ଶ ∗ ൫√1 + sin ߠ − 1൯ ∗ ൬cos ൬ − ൰ cos ߠ − sin ൬ − ൰൰ = ܲ ∗ ݈ ∗ sin ߠ
4 2
4 2
݇∗݈
ߨ ߠ cos ߠ
ߨ ߠ
ܲ
∗ ቆ൫√1 + sin ߠ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰ −
ቇ ∗ ߠ = 0
ߠ
4 2 sin ߠ
4 2
݇∗݈
݇ ∗ =

Rome, AUGUST 2013

݇∗݈
ߨ ߠ cos ߠ
ߨ ߠ
ܲ
∗ ቆ൫√1 + sin ߠ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰ −
ቇ
ߠ
4 2 sin ߠ
4 2
݇∗݈

Pag. 51


A.A. 2012/2013

Buckling
ߨ ߠ cos ߠ
ߨ ߠ
ܲ௖௥ = ݇ ∗ ݈ ∗ ൫√1 + sin ߠ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰
4 2 sin ߠ
4 2
ܲ௖௥
ߨ ߠ cos ߠ
ߨ ߠ
= ൫√1 + sin ߠ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰
4 2 sin ߠ
4 2
݇∗݈

5.4.1.2
5.4.1.2.1

Real beam
Small displacements
deformed shape:
݇ ∗ ݈ ଶ ∗ ൫ඥ1 + ߠ − ߠ଴ − 1൯ ∗ ሺ1 − ߠሻ = ܲ ∗ ݈ ∗ ߠ

ܲ
൫ඥ1 + ߠ − ߠ଴ − 1൯ ∗ ሺ1 − ߠሻ
݇ ∗ ݈ ∗ ቆ
−
ቇ ∗ ߠ = ݇ ∗ ∗ ߠ = 0
݇∗݈
ߠ
ܲ
൫ඥ1 + ߠ − ߠ଴ − 1൯ ∗ ሺ1 − ߠሻ
−
݇ ∗ = ݇ ∗ ݈ ∗ ቆ
ቇ
݇∗݈
ߠ

൫ඥ1 + ߠ − ߠ଴ − 1൯ ∗ ሺ1 − ߠሻ

ߠ
ܲ௖௥
൫ඥ1 + ߠ − ߠ଴ − 1൯ ∗ ሺ1 − ߠሻ
=
ߠ
݇∗݈

ܲ௖௥ = ݇ ∗ ݈ ∗

5.4.1.2.2

Large displacements

deformed shape:
ߨ ߠ
ߨ ߠ
݇ ∗ ݈ ଶ ∗ ൫ඥ1 + sin ߠ − sin ߠ଴ − 1൯ ∗ ൬cos ൬ − ൰ cos ߠ − sin ൬ − ൰൰ = ܲ ∗ ݈ ∗ sin ߠ
4 2
4 2
݇∗݈
ߨ ߠ cos ߠ
ߨ ߠ
ܲ
∗ ቆ൫ඥ1 + sin ߠ − sin ߠ଴ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰ −
ቇ ∗ ߠ = 0
ߠ
4 2 sin ߠ
4 2
݇∗݈
݇ ∗ =

݇∗݈
ߨ ߠ cos ߠ
ߨ ߠ
ܲ
∗ ቆ൫ඥ1 + sin ߠ − sin ߠ଴ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰ −
ቇ
ߠ
4 2 sin ߠ
4 2
݇∗݈

ߨ ߠ cos ߠ
ߨ ߠ
ܲ௖௥ = ݇ ∗ ݈ ∗ ൫ඥ1 + sin ߠ − sin ߠ଴ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰
4 2 sin ߠ
4 2
ߨ ߠ cos ߠ
ߨ ߠ
ܲ௖௥
= ൫ඥ1 + sin ߠ − sin ߠ଴ − 1൯ ∗ ൬cos ൬ − ൰
− sin ൬ − ൰൰
4 2 sin ߠ
4 2
݇∗݈

5.4.1.3

Results
situations:

Rome, AUGUST 2013

Pag. 52


A.A. 2012/2013

Buckling

Critical load - Small displacements

Figure 5.15

1,00

P/(kL)

I.B.
0,75
0,50
R.B.

0,25
0,00

-45,000

-15,000

15,000

45,000

-0,25
-0,50
-0,75
-1,00
θ (°)
I.B.

R.B. - 0,1

R.B. - 0,2

R.B. - 0,3

Critical load - Large displacements
Figure 5.16

1,00

P/(kL)

0,75
0,50
I.B.
0,25
R.B.
0,00
-45,000

-15,000

15,000

45,000

-0,25
-0,50
-0,75
-1,00
θ (°)
I.B.

R.B - 0.1

R.B - 0.2

R.B - 0.3

2) Critical load becomes lower for positives values of angle θ and this means that postcritical behavior is stable.
imperfection of system, critical load always becomes smaller.

Rome, AUGUST 2013

Pag. 53


A.A. 2012/2013
5.4.2
5.4.2.1
5.4.2.1.1
5.4.2.1.1.1

Buckling

Incremental method
Real beam
SAP2000
Modeling
1) We use same models previously described in case B, only with substitution of
translational spring on the top of the beam with the sloping one, fixed to the base.
2) Sloping spring is modeled by a beam element to which we assign fictitious material
with elastic modulus equal to spring stiffness and zero weight per unit volume.

Results
5.4.2.1.1.2

analytical method:

PL/k
1,25

Figure 5.17

1
0,75
0,5
0,25

-90,000

-60,000

0
-30,000
0,000
-0,25

30,000

60,000

90,000

-0,5
θ (°)
Analytical

SAP - Tolerance=0,1

1,25

Figure 5.18

PL/k

1
0,75
0,5
0,25

-90,000

-60,000

-30,000

0
0,000
-0,25

30,000

60,000

90,000

-0,5
θ (°)
Analytical

SAP - Tolerance=0,1

s
s
Rome, AUGUST 2013

Pag. 54


A.A. 2012/2013

Buckling


Figure 5.19

1,25

PL/k

1
0,75
0,5
0,25

-90,000

-60,000

-30,000

0
0,000

30,000

60,000

90,000

-0,25
-0,5
θ (°)
Analytical

SAP - Tolerance=0,1

Small displacements - SAP - Tolerance=0,1
Figure 5.20

PL/k

1,25
1
0,75
0,5
0,25
0
-90

-60

-30

0

30

60

90

-0,25
-0,5
θ (°)
θ = 0,1 L

Rome, AUGUST 2013

θ = 0,2 L

θ = 0,3 L

Pag. 55


A.A. 2012/2013

Buckling

Large displacements - θ = 0,1 L

Figure 5.20

1,250

PL/k

1,000
0,750
0,500
0,250

-90,000

-60,000

-30,000

0,000
0,000

30,000

60,000

90,000

-0,250
-0,500
θ (°)
Analytical


1,250

PL/k

Figure 5.21
1,000
0,750
0,500
0,250

-90,000

-60,000

0,000
-30,000
0,000

30,000

60,000

90,000

-0,250
-0,500
θ (°)
Analytical

Rome, AUGUST 2013


Pag. 56


A.A. 2012/2013

Buckling


Figure 5.22

1,250

PL/k

1,000
0,750
0,500
0,250

-90,000

0,000
-30,000
0,000

-60,000

30,000

60,000

90,000

-0,250
-0,500
θ (°)
Analytical


Large displacements - SAP - Tolerance=0,0001
Figure 5.23

1,25

PL/k

1
0,75
0,5
0,25
0
-90

-60

-30

0

30

60

90

-0,25
-0,5
θ (°)
θ = 0,1 L

Rome, AUGUST 2013

θ = 0,2 L

θ = 0,3 L

Pag. 57

Exercise n.6: Evolution of the load-displacement curve of a three-hinged arch

A.A. 2012/2013

Buckling

EXERCISE N.6

e
EVOLUTION OF THE LOAD-DISPLACEMENT CURVE OF A THREE-HINGED ARCH

6.1

Outline
1) Identify numerically the load-displacement curve of a three-hinged arch with
lowering H0/L0 = 0.1, highlighting different mechanism of instability at varying of
slenderness. In particular, consider two distinct values of slenderness: λ1 = 50
(squat beam) and λ2 = 75 (slender beam).

Figure 6.1

2) Geometry data:
• ‫ܮ‬଴ = 4 ݉ ‫ ݉ܽ݁ܤ‬ℎ‫݊݋݅ݐ݆ܿ݁݋ݎ݌ ݈ܽݐ݊݋ݖ݅ݎ݋‬
•

•
•
•

ு బ
௅ బ

= 0,1 ‫ܿݎܣ‬ℎ ݈‫݃݊݅ݎ݁ݓ݋‬

‫ܪ‬଴ = 4 ݉ ‫݊݋݅ݐ݆ܿ݁݋ݎ݌ ݈ܽܿ݅ݐݎ݁ݒ ݉ܽ݁ܤ‬
ߠ଴ = 5,71° ‫݁݌݋݈ݏ ݉ܽ݁ܤ‬
‫ݐ݈݃݊݁ ݉ܽ݁ܤ ݉ 4 = ܮ‬ℎ

•

ߣଵ = 50 ݈ܵ݁݊݀݁‫ݏݏ݁݊ݎ‬

ߩ = ఒ = 0,0804 ݉ ܴܽ݀݅‫݊݋݅ݐܽݎݕ݃ ݂݋ ݏݑ‬
௅

݈ = ඥ12 ߩଶ = 0,2785 ݉ ܵ݁ܿ‫݁݀݅ݏ ݊݋݅ݐ‬
‫ ݈ = ܣ‬ଶ = 0,0776 ݉ଶ ܵ݁ܿ‫ܽ݁ݎܽ ݊݋݅ݐ‬

‫=ܬ‬
•

௟ర
ଵଶ

= 0,0005 ݉ସ ‫ܽ݅ݐݎ݁݊ܫ‬

ߣଶ = 75 ݈ܵ݁݊݀݁‫ݏݏ݁݊ݎ‬

ߩ = ఒ = 0,0536 ݉ ܴܽ݀݅‫݊݋݅ݐܽݎݕ݃ ݂݋ ݏݑ‬
௅

݈ = ඥ12 ߩଶ = 0,1857 ݉ ܵ݁ܿ‫݁݀݅ݏ ݊݋݅ݐ‬
‫ ݈ = ܣ‬ଶ = 0,0345 ݉ଶ ܵ݁ܿ‫ܽ݁ݎܽ ݊݋݅ݐ‬
‫ = ܬ‬ଵଶ = 0,0001 ݉ସ ‫ܽ݅ݐݎ݁݊ܫ‬
௟ర

Rome, AUGUST 2013

Pag. 58


A.A. 2012/2013
6.2

Buckling

Analytical method
2) We make following assumptions to study the stability of elastic equilibrium:
• Large displacements
• Equilibrium on deformed shape
This means that we do a complete discussion of problem, without any
simplification.
3) First of all, we write expressions of kinematic quantities on deformed shape with
geometric relations:
‫ܮ = ܪ‬଴ ∗ tan ߠ = ‫ ∗ ܮ‬cos ߠ଴ ∗ tan ߠ
‫= ∗ܮ‬

‫ܪ‬
‫ ∗ ܮ‬cos ߠ଴ ∗ tan ߠ
=

sin ߠ
sin ߠ

∆‫ܮ = ܮ‬଴ − ‫ܮ = ∗ܮ‬଴ − ൬1 −

cos ߠ଴ ∗ tan ߠ
൰
sin ߠ

Figure 6.2

6.2.1

Congruence
1) We write congruence equation:
߂‫ܮ‬
ߝ=
=1−

‫ܮ‬
sin ߠ

6.2.2


ߪ = ‫ߝ ∗ ܣܧ = ܰ ߝ ∗ ܧ‬
ܰ = ‫ ∗ ܣܧ‬൬1 −

6.2.3

൰
sin ߠ

Equilibrium
෍ ‫ܨ‬௭ = 0
ܲ − 2 ∗ ܰ ∗ sin ߠ = 0

Rome, AUGUST 2013

Pag. 59


A.A. 2012/2013
6.2.4

Buckling

Solution
൰ ∗ sin ߠ = 0
sin ߠ
ܲ = 2 ∗ ‫ ∗ ܣܧ‬ሺsin ߠ − cos ߠ଴ ∗ tan ߠሻ

ܲ − 2 ∗ ‫ ∗ ܣܧ‬൬1 −

ܲ
= 2 ∗ ‫ ∗ ܣ‬ሺsin ߠ − cos ߠ଴ ∗ tan ߠሻ
‫ܧ‬

2) We report the evolution of vertical load P at increasing of vertical displacement v:

Figure 6.5

Load-Displacement

P/E (m^2)
0,0001
0,00008
0,00006

Pcrit/E
2,94E-05 m^-2

0,00004
0,00002
0

Pcrit/E
1,31E-05 m^-2

-0,00002
-0,00004
0

0,2

0,4

0,6

0,8

1

Displacement v (m)
λ1=50

λ2=75

3) Structure has a step-through behavior: load P increases till critical value, then it
decreases to reach the minimal one (it is the same absolute value) and, after that, it
restarts to increase till this yield point of beam.
4) Structure has this behavior because, when load reaches critical value, it turns from
stable shape to unstable shape and its bearing capacity decreases till it reaches a
new stable configuration.

Figure 6.6

Rome, AUGUST 2013

Pag. 60


A.A. 2012/2013

Buckling
5) During first step, beams are shortened, then they start to be stretched until failure.
Magnitude of strength properties are inversely proportional to beam slenderness.
6) In both considered cases, structure has a step-through behavior because axial force
in beam is lower than maximum value that they can carry without buckling:
ܲ௘௨,ఒభ ߨ ଶ ∗ ‫ܬ‬ଵ
1 ܲ௖௥,ఒభ
=
= 3,06 ∗ 10ିସ ݉ଶ >
= 1,47 ∗ 10ିହ ݉ଶ
ଶ
2 ‫ܧ‬
‫ܧ‬
‫ܮ‬
ܲ௘௨,ఒమ ߨ ଶ ∗ ‫ܬ‬ଶ
1 ܲ௖௥,ఒమ
=
= 6,05 ∗ 10ିହ ݉ଶ >
= 6,55 ∗ 10ି଺ ݉ଶ
ଶ
2 ‫ܧ‬
‫ܧ‬
‫ܮ‬
7) When slenderness increase, critical load decreases and it can be lower than
buckling one, so structure cannot develop its snap-through behavior because
beams lose their stiffness for buckling failure.

Figure 6.7

6.3
6.3.1
6.3.1.1

Incremental method
SAP2000
Modeling
1) The structure is modeled by two beam element, fixed at bottom ends by external
hinges. Middle hinge is modeled by assigning M3 releases to top ends of beam.
2) We define two different sections with geometric dimensions previously described.
3) We assign a vertical force P on middle hinge, that will be used to set pushover
analysis.

Figure 6.8

Rome, AUGUST 2013

Pag. 61


A.A. 2012/2013

Buckling
4) We define a nonlinear static load cases called P-LD, that use base load pattern P,
previously defined, and considers geometric nonlinearity parameters P-Delta and
large displacements.

Figure 6.9

6.3.1.2

Results
analytical method:

Load-Displacement

Figure 6.10
0,0001
0,00008

P/E (1/m^2)

0,00006
0,00004
0,00002
0
0

0,2

0,4

0,6

0,8

1

-0,00002
-0,00004

Displacement v (m)
Analytical - λ1=50

Rome, AUGUST 2013

Analytical - λ2=75

Pag. 62

FACULTY OF CIVIL AND INDUSTRIAL ENGINEERING

Department of Structural and Geotechnical Engineering

A.A. 2012 – 2013
Course:

Steel Constructions

Dynamic analyzes of a cantilever beam

Professor:
Assistants:

Rome, November 2013

Student:

Dynamic analyses of a cantilever beam

A.A. 2012/2013

INDEX
1. Outline ................................................................................................................................... 1
2. Modeling ................................................................................................................................ 1
2.1 ANSYS ...................................................................................................................................................... 1
2.1.1 BEAM3 element............................................................................................................................... 2
2.1.2 PLANE183 element .......................................................................................................................... 3

3. Analyzes ................................................................................................................................. 4
3.1 Modal analysis ......................................................................................................................................... 4
3.1.1 Results ............................................................................................................................................. 5
3.1.1.1 Case 1 - L=1 m ......................................................................................................................... 5
3.1.1.2 Case 2 - L=2 m ......................................................................................................................... 6
3.2 Transient analysis .................................................................................................................................... 8
3.2.1 Results ...........................................................................................................................................11
3.2.1.1 Case 1 - L=1 m .......................................................................................................................11
3.2.1.2 Case 2 - L=2 m .......................................................................................................................13
3.3 Fatigue analysis .....................................................................................................................................16
3.3.1 Material fatigue properties ...........................................................................................................16
3.3.2 Events and loadings .......................................................................................................................17
3.3.3 Locations .......................................................................................................................................18
3.3.4 Rainflow counting method ............................................................................................................18
3.3.5 Miner's rule ...................................................................................................................................18
3.3.6 Results ...........................................................................................................................................19
3.3.6.1 Case 1 - L=1 m .......................................................................................................................19
3.2.6.2 Case 2 - L=2 m .......................................................................................................................21

Rome, AUGUST 2013

Dynamic analyses of a cantilever be
eam

1.

A.A. 2012/2013

Outline
1) We report d
dynamic analyzes of a simple cantilever beam shown below:

Figure 1

2) Material dat
ata:
• ‫ ܧ‬ൌ 2,068 ∗ 10ଵଵ ܰ/݉ଷ ‫ݏݏ݂݂݁݊݅ݐݏ ܿ݅ݐݏ݈ܽܧ‬
• ߩ ൌ 7830 ‫݉/݃ܭ‬ଷ ‫ݕݐ݅ݏ݊݁ܦ‬
• ߥ ൌ 0,3 ܲ‫݊݋ݏݏ݅݋‬
er
3) We conside two different cases:
• Cas 1
ase
- L=1m
- Cyclic load (harmonic) at the end of the beam
• Cas 2
ase
- L=2m
- Two cyclic loads (harmonic) in the middle and at the end of the beam.
d
hree different anlyzes:
4) We make th
• Mo analysis
odal
• Tran
ansient analysis under a time-varying load
• Fat
atigue analysis
5) We model structure with two different element type:
s
• BEA
AM3 (2D elastic beam)
• PLA
ANE183 (2D 8-node structural solid)

2.
2.1

Modeling
ANSYS
1) ANSYS is a general purpose finite element modeling package for numerically solving
g
e
a wide varie of mechanical problems. These problems incl
iety
lude: static/dynamic
structural analysis (both linear and non-linear), heat transfe and fluid problems, as
an
er
well as acou
ustic and electro-magnetic problems.
2) In general, a finite element solution may be broken into the following three stages,
e
that can be used for setting up any finite element analysis.
•

Rome, November 2013

Preproc
cessing: defining the problem
The majo steps in preprocessing are given below:
ajor
- Def
fine keypoints/lines/areas/volumes
- Def
fine element type and material/geometric proper
rties
- Mesh lines/areas/volumes as required
Pag. 1

A.A. 2012/2013


•

•

2.1.1

Solution: assigning loads, constraints and solving
We specify the loads (point or pressure), constraints (translational and
rotational) and finally solve the resulting set of equations.
Postprocessing: further processing and viewing of the results
In this stage one may wish to see:
- Lists of nodal displacements
- Element forces and moments
- Deflection plots
- Stress contour diagrams

BEAM3 element
1) BEAM3 is a uniaxial element with tension, compression, and bending capabilities.
The element has three degrees of freedom at each node: translations in the nodal x
and y directions and rotation about the nodal z-axis.
2) The element is defined by two nodes, the cross-sectional area, the area moment of
inertia, the height, and the material properties.

Figure 2

3) We report the command line codes to create model of the cantilever beam with
BEAM3 element in ANSYS, in both cases analyzed:
(Entering in preprocessor section)
/PREP7
(Setting general constants)
Length=1
Width=0.01
Height=0.01
Elastic modulus=2.06E11
Poisson ratio=0.3
Density=7830
(Defining geometry)
K,1,0,0
K,2,Length,0
L,1,2

K,1,0,0
K,2,Length,0
K,3,2*Length,0
L,1,2
L,2,3

(Defining element type and its real constants)
ET,1,BEAM3
R,1,Width*Height,Width*(Height**3)/12,Height
Rome, November 2013

Pag. 2


A.A. 2012/2013

(Defining element material properties)
MP,EX,1,Elastic modulus
MP,PRXY,1,Poisson ratio
MP,DENS,1,Density
(Defining mesh size and meshing)
LESIZE,ALL,Length/10
LMESH,ALL
FINISH

2.1.2

PLANE183 element
1) PLANE183 is a higher order 2-D, 8-node or 6-node element. PLANE183 has
quadratic displacement behavior and is well suited to modeling irregular meshes.
2) This element is defined by 8 nodes or 6-nodes having two degrees of freedom at
each node: translations in the nodal x and y directions. The element may be used as
a plane element (plane stress, plane strain and generalized plane strain) or as an
axisymmetric element.
3) This element has plasticity, hyperelasticity, creep, stress stiffening, large deflection,
and large strain capabilities. It also has mixed formulation capability for simulating
deformations of nearly incompressible elastoplastic materials, and fully
incompressible hyperelastic materials.

Figure 3

4) We report the command line codes to create model of the cantilever beam with
PLANE183 element in ANSYS,in both cases analyzed.
(Entering preprocessor)
/PREP7
(Setting general constants)
Length=1
Width=0.01
Height=0.01
Elastic modulus=2.06E11
Poisson ratio=0.3
Density=7830
(Defining element type and its real constants)
ET,1,PLANE183
KEYOPT,1,1,0
(Element shape: 8-node quadrilateral)
KEYOPT,1,3,3
(Element behavior: plane stress with thickness)
R,1,0.01
Rome, November 2013

Pag. 3

A.A. 2012/2013


(Defining element material properties)
MP,EX,1,Elastic modulus
MP,PRXY,1,Poisson ratio
MP,DENS,1,Density
(Defining geometry)
RECTNG,0,1,-0.005,0.005,

RECTNG,0,2,-0.005,0.005,

(Defining mesh size and meshing)
LSEL,S,LINE,,2,4,2,0
LESIZE,ALL,,,2,
LSEL,NONE
LSEL,S,LINE,,1,3,2,0
LESIZE,ALL,,,10,
LSEL,NONE
LSEL,ALL
AMESH,ALL
FINISH

3.
3.1

Analyzes
Modal analysis
1) Modal analysis determines the vibration characteristics (natural frequencies and
mode shapes) of a structure or a machine component. It can also serve as a starting
point for another, more detailed, dynamic analysis, such as a transient dynamic
analysis, a harmonic analysis, or a spectrum analysis. The natural frequencies and
mode shapes are important parameters in the design of a structure for dynamic
loading conditions.
2) We report the command line codes to perform modal analysis of the cantilever
beam with in all cases analyzed:
(Entering in solution processor)
/SOLU
(Defining analysis type)
ANTYPE,MODAL
(Setting option for analysis type)
MODOPT,SUBSP,5
EQSLV,FRONT
MXPAND,5
(Applying constraints)
DK,1,ALL
BEAM3-Nodal constraint
or
DL,4,,ALL
PLANE183-Linear constraint
(Solving)
SOLVE
FINISH

Rome, November 2013

Pag. 4


3.1.1

A.A. 2012/2013

Results
1) We report the command line codes to see results of modal analysis in all cases
analyzed:
(Entering postprocessor)
/POST1
(Selecting results set to read)
SET,LIST
SET,FIRST First mode
(Plotting deformed shape)
PLDISP

3.1.1.1

Case 1 - L=1 m
1) We report deformed shape for all modes, compared between two models created:

Figure 4

Figure 5

Figure 6

Rome, November 2013

Pag. 5

A.A. 2012/2013


Figure 7

Figure 8

Mode
1
2
3
4
5

3.1.1.2

BEAM3 PLANE183
f (Hz)
f (Hz)
8,2856
8,2975
51,921
51,981
145,38
145,54
285,02
285,5
471,72
473,56

Error
0,14%
0,12%
0,11%
0,17%
0,39%

Case 2 - L=2 m
1) We report deformed shape for all modes, compared between two models created:

Figure 9

Rome, November 2013

Pag. 6

eam

A.A. 2012/2013

Figure 10

Figure 11

Figure 12

Figure 13

Rome, November 2013

Pag. 7

A.A. 2012/2013


Mode
1
2
3
4
5

1.3.1.2
3.2
Figure 1.5

BEAM3 PLANE183
f (Hz)
f (Hz)
2,0714
2,073
12,981
12,99
36,346
36,366
71,223
71,254
117,74
117,78

Error
0,08%
0,07%
0,05%
0,04%
0,03%

Transient analysis
1) Transient analysis is used to determine the dynamic response of a structure under
the action of any general time-dependent loads. It is used to determine the timevarying displacements, strains, stresses, and forces in a structure as it responds to
any transient loads. The time scale of the loading is such that the inertia or damping
effects are considered to be important.
2) For case 1,we apply an harmonic cyclic load at the end of the beam. Frequency of
the load is set equal to frequency of the first mode of structure from modal
analysis:
݂(‫ܲ = )ݐ‬଴ ∗ cos(Ωt)
•
•

ܲ଴ = 10 ܰ
Ω = 2Π ∗ ݂ଵ = 8,28 ‫ݏ/݀ܽݎ‬

Figure 14

CASE 1 -

f (t) = P0*COS(Ωt)

15
10

f (kN)

5
0
-5

Figure 1.6

-10
-15
0

0,5

1

1,5

2

2,5

t (s)

3) For case 2,we apply two harmonic cyclic loads: the first one in the middle and the
second the at the end of the beam. Frequency of first load is set equal to frequency
of the first mode of structure from modal analysis, while frequency of second load
is set 1,6 times greater:
݂௜ (‫ܲ = )ݐ‬଴ ∗ cos(Ω୧ t)
• ܲ଴ = 10 ܰ
• Ωଵ = 2Π ∗ ݂ଵ = 13,01 ‫ݏ/݀ܽݎ‬
• Ωଶ = 1,6 ∗ (2Π ∗ ݂ଵ ) = 20,81 ‫ݏ/݀ܽݎ‬

Rome, November 2013

Pag. 8

A.A. 2012/2013


Figure 15

CASE 2 -

f (t) = P0*COS(Ωt)

15
10

f (kN)

5
0
-5
-10
-15
0

0,5

1

1,5

2

2,5

t (s)
MIDDLE

END

3) We report the command line codes to perform transient analysis of the cantilever
beam with in all cases analyzed:
(Entering in solution processor)
/SOLU
(Defining analysis type)
ANTYPE,TRANS
(Applying constraints)
DK,1,ALL
BEAM3-Nodal constraint
or
DL,4,,ALL
PLANE183-Linear constraint
(Defining load vector from external .txt file)
CASE1
NSTEP=500
*DIM,FORCE,TABLE,NSTEP,1
*TREAD,FORCE,'f','txt','Desktopeser1', ,
CASE2
NSTEP=500
*DIM,FORCE2,TABLE,NSTEP,1
*TREAD,FORCE2,'f2','txt','Desktopeser2', ,
(Applying load with a do-loop and solving)
CASE1 - BEAM3
TM_START=1E-8
TM_INCR=0.005
TM_END=NSTEP*TM_INCR-TM_INCR
*DO,TM,TM_START,TM_END,TM_INCR
Rome, November 2013

Pag. 9


A.A. 2012/2013

TIME,TM
FK,2,FY,FORCE(TM)
SOLVE
*ENDDO
FINISH
CASE2 - BEAM3
TM_START=1E-8
TM_INCR=0.01
TIME,TM
FK,2,FY,FORCE2(TM)
FK,3,FY,FORCE3(TM)
SOLVE
*ENDDO
FINISH
CASE1 - PLANE183
TM_START=1E-8
TM_INCR=0.005
TIME,TM
F,2,FY,FORCE(TM)
F,22,FY,FORCE(TM)
Load is divided into 5 parts and is applied to 5
F,23,FY,FORCE(TM)
nodes along the vertical section
F,24,FY,FORCE(TM)
F,25,FY,FORCE(TM)
SOLVE
*ENDDO
FINISH
CASE2 - PLANE183
NSTEP=500
TM_START=1E-8
TM_INCR=0.01
TIME,TM

Rome, November 2013

Pag. 10

A.A. 2012/2013

eam

F,606
6,FY,FORCE2(TM)
F,202
2,FY,FORCE2(TM)
F,1206
06,FY,FORCE2(TM)
F,1207
07,FY,FORCE2(TM)
F,1208
08,FY,FORCE2(TM)
F,2,FY
FY,FORCE3(TM)
F,402
2,FY,FORCE3(TM)
F,403
3,FY,FORCE3(TM)
F,404
4,FY,FORCE3(TM)
F,405
5,FY,FORCE3(TM)
SOLV
VE
*ENDD
DDO
FINIS
SH

3.2.1
3.2.1.1

Load is divided into 5 parts and is applied to 5
nodes along the verti section
ical

Results
Case 1 - L=1m
3) We report the command line codes to see results of transie analysis in case 1:
ient
(Enterin in time-history postprocessor)
ing
/POST
ST26
(Definin free end displacement as variable)
ing
NSOL
L,2,2,U,Y,UY
BEAM3
or
NSOL
L,2,24,U,Y,UY
PLANE183
STORE
RE,MERGE
(Plottin variable vs. time)
ng
PLVA
AR,2
4) The response curve from ANSYS:

Figure 16

Rome, November 2013

Pag. 11

A.A. 2012/2013

eam

5) Adding dam
amping to the model, response curve become:
(Enterin preprocessor)
ing
/PREP
EP7
(Definin constant of stiffness matrix multiplier to obtai damping matrix)
ing
ain
BETAD
AD,0.002

Figure 17

6) We report t comparison of results between two models analyzed:
the
an

Response curve

Figure 18

1,50

Displacements (m)

1,00

0,50

0,00

-0,50

-1,00

-1,50
0,00

0,50

1,00

1,50

2,00

2,50

Time (s)
BEAM3

Rome, November 2013

PLANE183

Pag. 12

A.A. 2012/2013


Response curve with damping

Figure 19
0,20
0,15
0,10

Displacements (m)

0,05
0,00
-0,05
-0,10
-0,15
-0,20
0,00

0,50

1,00

1,50

2,00

2,50

Time (s)
BEAM3

3.2.1.2

PLANE183

Case 2 - L=2 m
1) We report the command line codes to see results of transient analysis in case 1:
(Entering in time-history postprocessor)
/POST26
(Defining free end displacement as variable)
NSOL,2,2,U,Y,UY-END
BEAM3
NSOL,3,12,U,Y,UY-MIDDLE
or
NSOL,2,1207,U,Y,UY-MIDDLE PLANE183
NSOL,3,404,U,Y,UY-END
STORE,MERGE
(Plotting variable vs. time)
PLVAR,2
2) The response curve from ANSYS:

Rome, November 2013

Pag. 13

eam

A.A. 2012/2013

Figure 20

3) Adding damping to the model, response curve become:
(Enterin preprocessor)
ng
/PREP
EP7
(Definin constant of stiffness matrix multiplier to obtai damping matrix)
ng
ain
BETAD
AD,0.01

Figure 21

In this damp case, we increased number of substeps to hi
ped
ighlight the
development of response.

Rome, November 2013

Pag. 14

A.A. 2012/2013


4) We report the comparison of results between two models analyzed:

Figure 22

Response curves
4,00
3,00
2,00

Displacements (m)

1,00
0,00
-1,00
-2,00
-3,00
-4,00
0,00

2,00

4,00

6,00

8,00

10

Time (s)
BEAM3 - MIDDLE

BEAM3 -END

PLANE183 - MIDDLE

PLANE183 - END

Response curves with damping
Figure 23

0,60

0,40

Displacements (m)

0,20

0,00

-0,20

-0,40

-0,60
0,00

2,00

4,00

6,00

8,00

10,00

Time (s)
BEAM3 - MIDDLE
PLANE 183 - MIDDLE

Rome, November 2013

BEAM3 - END
PLANE 183 - END

Pag. 15

A.A. 2012/2013


3.3

Fatigue analysis
1) Fatigue is the phenomenon in which a repetitively loaded structure fractures at a
load level less than its ultimate static strength. For instance, a steel bar might
successfully resist a single static application of a 300 kN tensile load, but might fail
after 1,000,000 repetitions of a 200 kN load.
2) The primary factors that contribute to fatigue failures include:
• Number of load cycles experienced
• Range of stress experienced in each load cycle
• Mean stress experienced in each load cycle
• Presence of local stress concentrations
3) The procedure normally consists of four general steps:
• Establish the size (the number of locations, events, and loadings), define the
fatigue material properties, identify stress locations, and define stress
concentration factors.
• Store stresses at locations of interest for various events and loadings; assign
event repetitions and scale factors.
• Activate the fatigue calculations.
• Review the results.
4) We perform fatigue analysis only for PLANE183-models with damping in case 1 and
case 2, because ANSYS is not able to read stress results from previous analysis for
line-element.

3.3.1

Material fatigue properties
1) Material fatigue properties are described by:

where Su=690 MPa is the ultimate strength and Se is the endurance limit (fatigue
limit). We assume the ratio Se/ Su=0.6.

Figure 24

S-N curve
Stress amplitude (N/m^2)

8,00E+08
7,00E+08
6,00E+08
5,00E+08
4,00E+08
3,00E+08
2,00E+08
1,00E+08
0,00E+00
1,00E+00 1,00E+01 1,00E+02 1,00E+03 1,00E+04 1,00E+05 1,00E+06 1,00E+07
Number of Cycles

Rome, November 2013

Pag. 16


3.3.2

A.A. 2012/2013

Events and loadings
1) An event is a set of stress conditions that occur at different times during a unique
stress cycle.
2) A loading is one of the stress conditions that is part of an event.
3) The alternating stress intensity is a measure of the difference in stress state
between any two loadings. The program does not adjust the alternating stress
intensity for mean-stress effects.
4) We rely on response curves from previous transient analysis to define events and
loads. We choose, as time steps for storing stress, those corresponding to peaks of
displacement in the stationary part of the answer and group them as shown below:

Figure 25

STEP t (s) u (m)
321 1,6 0,174
333 1,66 -0,174

CASE 1
Event no. Load no. f (N) No. of repetitions
1
1
-1,457
500
1
2
1,316
500

Figure 26

Rome, November 2013

Pag. 17

A.A. 2012/2013


STEP
497
518
546
571
592
615
644
665
687
717

3.3.3

t (s)
4,96
5,17
5,45
5,7
5,91
6,14
6,43
6,64
6,86
7,16

CASE 2
Event Load
No. of
u-Mid (m) u-End (m)
no. no. f-Mid (N) f-End (N) repetitions
0,163
0,469
1
1
-1,079
-8,981
1000
-0,148
-0,422
2
2
-2,976
7,158
1000
0,097
0,299
3
3
-1,966
9,503
1000
-0,153
-0,445
4
4
3,030
7,221
1000
0,161
0,459
5
5
1,022
-8,941
1000
-0,107
-0,317
6
6
-2,499
-5,127
1000
0,136
0,402
7
7
-3,687
-2,860
1000
-0,167
-0,479
8
8
-0,327
9,986
1000
0,129
0,372
9
9
3,078
-1,854
1000
-0,115
-0,347
10
10
4,326
-2,248
1000

Locations
1) A location is a node in your model for which fatigue stresses are to be stored.
2) In both cases, we define three locations along beam for which fatigue stress are to
be stored
• Fixed end
• Middle
• Free end
Selected nodes are those on the top of the beam.

3.3.4

Rainflow counting method
1) Structures are usually subjected to a variety of maximum and minimum stresses,
which occur in unknown (or even random) order. Therefore, you must take care to
achieve an accurate count of the number of repetitions of all possible stress ranges,
in order to obtain a valid fatigue usage factor.
2) The ANSYS program automatically calculates all possible stress ranges and keeps
track of their number of occurrences, using a technique commonly known as the
"rain flow" range-counting method.
3) At a selected nodal location, a search is made throughout all of the events for the
pair of loadings (stress vectors) that produces the most severe stress-intensity
range. The number of repetitions possible for this range is recorded, and the
remaining number of repetitions for the events containing these loadings is
decreased accordingly. At least one of the source events will be "used up" at this
point; remaining occurrences of stress conditions belonging to that event will
subsequently be ignored. This process continues until all ranges and numbers of
occurrences have been considered.

3.3.5

Miner's rule
1) To account for variable amplitude loading, the S-N curve is supplemented by an
additional rule which permits the fatigue assessment to be undertaken.
2) Miner’s Rule is based upon the concept of fatigue damage and states that failure
occurs when:
ூ

෍
௜ୀ

•
•
Rome, November 2013

݊௜
= 1
ܰ௜

ni = number of applied load cycles of type i
Ni = maximum nuber of allowable load cycles of type i from S-N curve
Pag. 18


3.3.6.
3.3.6.1

A.A. 2012/2013

Results
Case 1 = L=1m
1) We report the command line codes to perform fatigue analysis:
(Entering in general postrocessor)
/POST1
(Selecting step results to read)
SET,LIST,999
SET,,, ,,, ,321
(Setting S-N table)
FP,1,10,1000,10000,100000,1000000,
FP,7, , , , , ,
FP,13, , , , , ,
FP,19, ,
FP,21,69.0e7,68.9e7,51.2e7,42.2e7,34.8e7,
FP,27, , , , , ,
FP,33, , , , , ,
FP,39, ,
(Setting locations)
FL,1,26,,,,Fixed end
FL,2,36,,,,Middle
(Storing stresses to define events and loadings)
FSNODE,26,1,1,
FSNODE,36,1,1,
FSNODE,22,1,1,
(Skipping to second step to read and storing stresses)
SET,LIST,999
SET,,, ,,, ,333
FSNODE,26,1,2,
FSNODE,36,1,2,
FSNODE,22,1,2,
(Assigning events)
FE,1,500,1,load1
(Calculating fatigue for every location)
FTCALC,1
FTCALC,2
FTCALC,3
2) We report the the results window:

Rome, November 2013

Pag. 19

eam

A.A. 2012/2013

Figure 27

The combin
ination of event 1, load 1 and event 1, load 2 produces an alternating
stress inten
nsity of 0.64756E+09 N/m2. The beam was subjec
cted to 500 cycles while
from the S- table the maximum cycles allowed at that stre intensity is 1618. The
-N
ess
partial usag value,0.30907, is the ratio of cycles used/cycle allowed.
age
es
The Cumulat Fatigue Usage value is sum of the partial us
lative
sage factor (Miner's rule)
and in this case it coincides with partial usage factor be
s
ecause there's only one
event.

Figure 28

Figure 29

Rome, November 2013

Pag. 20


3.3.6.2.

A.A. 2012/2013

Case 2 = L=2m
1) We report the command line codes to perform fatigue analysis:
(Entering in general postrocessor)
/POST1
(Selecting step results to read)
SET,LIST,999
SET,,, ,,, ,497
(Setting S-N table)
FP,1,10,1000,10000,100000,1000000,
FP,7, , , , , ,
FP,13, , , , ,
FP,13, , , , , ,
FP,19, ,
FP,21,69.0e7,68.9e7,51.2e7,42.2e7,34.8e7,
FP,27, , , , , ,
FP,33, , , , , ,
FP,39, ,
(Setting locations)
FL,2,606,,,,Middle
FL,3,402,,,,Free end
(Storing stresses to define events and loadings)
FSNODE,406,1,1,
FSNODE,606,1,1,
FSNODE,402,1,1,
(Skipping to following step to read and storing stresses)
SET,LIST,999
SET,,, ,,, ,546
FSNODE,406,3,1,
FSNODE,606,3,1,
FSNODE,402,3,1,
SET,LIST,999
SET,,, ,,, ,571
FSNODE,406,4,1,
FSNODE,606,4,1,
FSNODE,402,4,1,
SET,LIST,999
SET,,, ,,, ,615
FSNODE,406,6,1,
FSNODE,606,6,1,
FSNODE,402,6,1,

Rome, November 2013

Pag. 21


A.A. 2012/2013

SET,LIST,999
SET,,, ,,, ,644
FSNODE,406,7,1,
FSNODE,606,7,1,
FSNODE,402,7,1,
SET,LIST,999
SET,,, ,,, ,665
FSNODE,406,8,1,
FSNODE,606,8,1,
FSNODE,402,8,1,
SET,LIST,999
SET,,, ,,, ,687
FSNODE,406,9,1,
FSNODE,606,9,1,
FSNODE,402,9,1,
SET,LIST,999
SET,,, ,,, ,717
FSNODE,406,10,1,
FSNODE,606,10,1,
FSNODE,402,10,1,
(Assigning events)
FE,1,1000,1,load1
FE,2,1000,1,load2
FE,3,1000,1,load3
FE,4,1000,1,load4
FE,5,1000,1,load5
FE,6,1000,1,load6
FE,7,1000,1,load7
FE,8,1000,1,load8
FE,9,1000,1,load9
FE,10,1000,1,load10
(Calculating fatigue for every location)
FTCALC,1
FTCALC,2
FTCALC,3

Rome, November 2013

Pag. 22

eam

A.A. 2012/2013

2) We report the the results window:

Figure 30

The combin
stress inten
from the S-N table the maximum cycles allowed at that stress intensity is 36910.
S
s
The partial usage value,0.02709, is the ratio of cycles used/c
al
/cycles allowed.
The combin
stress inten
from the S-N table the maximum cycles allowed at that stress intensity is 69740.
S
s
al
/cycles allowed.
The combin
stress inten
from the S- table the maximum cycles allowed at that st
-N
tress intensity is 240200.
al
/cycles allowed.
The combin
stress inten
from the S- table the maximum cycles allowed at that str
-N
ress intensity is 1000000.
The partial usage value,0.001, is the ratio of cycles used/cyc allowed.
al
cles
The combin
stress inten
from the S- table the maximum cycles allowed at that str
-N
ress intensity is 1000000.
The partial usage value,0.001, is the ratio of cycles used/cyc allowed
al
cles
The Cumulat Fatigue Usage value is sum of the partial us
lative
sage factor (Miner's rule)

Rome, November 2013

Pag. 23

eam

A.A. 2012/2013

Figure 31

Figure 32

Rome, November 2013

Pag. 24

CM - elaborato RADDI

More Related Content

What's hot

Similar to CM - elaborato RADDI

More from Franco Bontempi Org Didattica

Recently uploaded

CM - elaborato RADDI