The document contains a series of physics problems and questions related to motion, forces, and dynamics, focusing on circular motion and its properties. It includes various scenarios involving mass, velocity, angular displacement, and centripetal force, while also posing challenges such as calculating tension in strings and maximum velocities. Each question requires an understanding of fundamental physics principles to derive the correct answers.











![(58)
65. ArodoflengthRandmass Mis freeto rotate about ahorizontalaxispassing throughhingeP as showninthe
figure. First it is taken aside suchthat it becomes horizontaland thenreleased.
At the lowest point the rod hits the block B of mass m and stops. If
mass ofrod is 75 kg, find mass ofthe block if it just complete the
circle.
R
m2
P
m1
66. Two particlesAand B are movingina horizontalplaneanticlockwiseontwo different concentric circles with
different constant angular velocities 2and respectively. Find the relative velocityofB w.r.t.Aafter time
t = /. (Take = 3rad/sec, r = 2m] (Both are moving in same sense)
2r
r
A B
X
Y
at t= 0
67. A flexible drive belt runs over a frictionless flywheel(seeFigure). The mass perunit length ofthe drive belt
is 1 kg/m, and the tension in the drive belt is 10N. The speed ofthe drive belt is 2m/s. The whole systemis
located on a horizontalplane. Find the normalforce (in N) exerted bythe belt on the flywheel.
T
T
v](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-13-638.jpg)
![SOLUTION [CIRCULAR MOTION]
(59)
1. (B) Centripetal acceleration is taken in frame of reference of
sphere because circular motion is in this frame
2. (C) Fcentripetal
= N - mg sin
N = Fcentripetal
+ mg sin
2
mV
mgsin
R
From conservation of energy
mg R sin =
1
2
mV2
2
mV
2 mg sin
R
3. (A) Suppose the body moves from A to B in time t. Then radius
vector describes the angle . Since the angle subtended at the
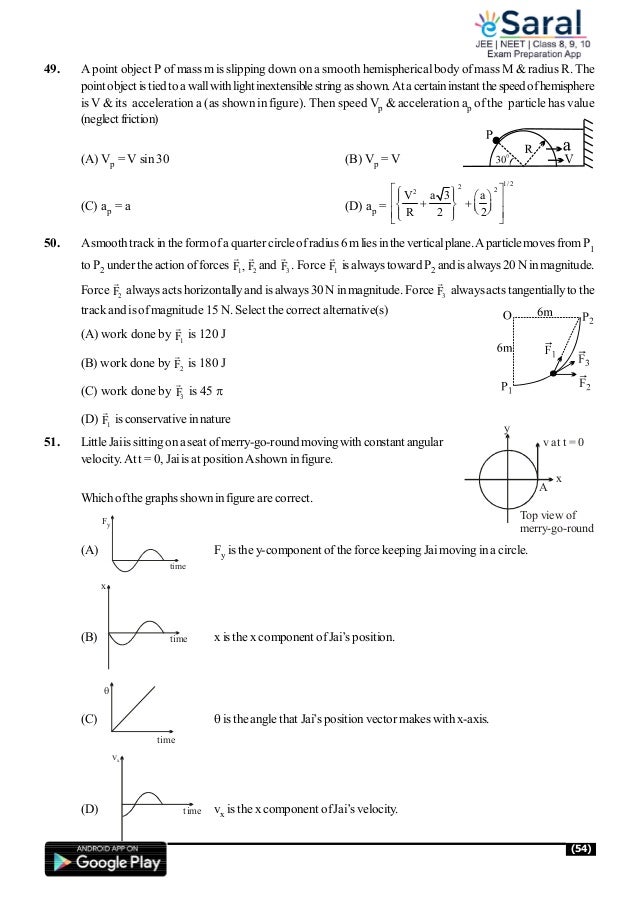
centre of the circle is twice that at the circumference. Hence the
angular velocity of the body is 2. Linear velocity = 2R
Acceleration
2 2 2
2
v 4R
4 R
R R
Put the values.
4. (B)
2
0
mv r
mg mg 1
r R
2
2
0
r
y v g r
R
For y to be maximum,
dy 2r
0 1
dr R
R
r
2
2
2
max 0 0
R R R
v g g
2 4R 4
0
max
gR
v
2
5. (D)
6. (B) Let O be the centre of circle and P the position of the point
at any time and Athe point about which angular velocity is to be
found.
N
O
P
T
A
Draw PN perpendicular to AP.
The velocity v at P is along PT,
the tangent at P.
Also if OAP = OPAs = ,
TPN = and therefore the resolved part of v along PN = v cos
.
Resolved part of v along PN
Angular velocity about A
AP
vcos v
2rcos 2r
CIRCULAR MOTION SOLUTION
7. (A) Given x = a sin t
y = b cos t
Radius vector ˆ ˆ
r xi yj
, = a sin t î + b cos t ˆ
j
Velocity vector dr
v
dt
,
d ˆ ˆ
(a sin i b cos t j)
dt
= a cos t ˆ
i – b sin t ˆ
j
Acceleration vector
dv
a
dt
= –a2
sin t ˆ
i – b2
cos t ˆ
j
= – 2 (a sin t ˆ
i + b cos t ˆ
j , 2
r
Forces 2
F ma m r
The magnitude of force
2
F ( m r)
,
2 2 2 2
F m r m x y
The direction of force is radially inwards.
8. (B)
9. (A)
10. (B) Angular velocity of particle P about point A,
A
AB
T 2r
A
2r
r
v
B
C
P
Angular velocity of particle
P about point C,
c
BC
T r
Ratio
A
c
/ 2r 1
/ r 2
](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-14-638.jpg)
![SOLUTION [CIRCULAR MOTION]
(60)
11. (D) Just after the release B moves downwards and A moves
horizontally leftwards with the same acceleration say a. Drawing
free body diagram of both A and B :
Tcos45 ma
or T 2ma ....(1)
mg Tcos45 ma
or mg ma ma
g
or a ... 2
2
Substituting this in (1) we get
mg
T
2
12. (C)
Consider an element of radius r and thickness dr.
Thickness of oil film is h.
dA = 2r dr, v = r
dF =
2
v 2
(dA) r dr
h h
dT = (dF)r =
3
2
r dr
h
T =
4
R
2h
or
4
T R
13. (B) x = displacement of rod w.r.t. sphere
R 2 R
2
2 2
y = displacement of sphere w.r.t. ground
My = M(x – y)
x R
y
2 4
14. (B) LMC
mV = mV0 + m(V0 + R) V = 2V0 + 2
AMC mVR = m(V0 + R)R + mR2
V = V0 + 2 R
solving = V/3 R
15. (A)
16. (A) So relative velocity in every case is of magnitude 2V
V1 = V2 = V3 = 2V
17. (C) Pi
= mv At final position, both the bead and ring are
rotating about axis through O and | to the plane.
Im
= mR2
, Iring
= mR2
I = Im
+ Iring
= 2mR2
Lfinal
= I = 2mR2
V'
R
= 2mRV'
Pf
=
final
L
R
= 2mV'
Pf
= Pi
2mV' = mV V' =
V
2
=
V'
R
=
V
2R
18. (C)
19. (C)
20. (C) v = S
dv 1 dS
dt dt
2 S
= · S
2 S
=
2
2
= a (tangential acceleration)
If required time is t, 2R =
2
1
at
2
solving we get t = 4 sec.
21. (A) Tsin = m2L sin
Tcos = mg
& hence, for constant ''
(angular speed), L
1
cos
2 1
1 2
L cos
L cos
=
3
· 2
2
=
3
2
22. (C) N – mgsin =
2
mv
R
2
1
mv2 = mgH
2
mv
R
=
2mgH
R
= 2mg
N =
mg
2
+ 2mg =
5mg
2](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-15-638.jpg)
![SOLUTION [CIRCULAR MOTION]
(61)
Contact force = mg
2
25 3
4 2
=
28
2
mg
23. (B) 1, g
R ˆ
V i
2
R cos =
R
2
= 60º
Rotated = 360º – 60º
= 300º or
5
3
; t =
5
3
24. (B) for complete circular motion
Vmin = 5gL
here geff = g sin 30º =
g
2
Vmin =
5
gL
2
25. (C)
2
1
mv mg
1 2
= 3mg
v1 =
5
g
2
now
1
2
mV0
2 + mg
1
2
=
1
2
mV1
2
V0 =
3g
2
=
3
2
26. (A) 1 = 2 =
1 = 2 = 1
27. a = g, eff
g g 2
45º
ma
equb.
mg
So geometry is like
T
2
m
2
mg 2
45º
g 2
2
m
Tcos45
2
Tsin45 mg 2
2
m 2g 2g
1
2mg
2
T 2
2g g
28. (D)
2
mv
10
r
2
1 r
mv 10 1J
2 2
29. (C) 30. (B) 31. (A) 32. (A)
33. (A) 34. (B) 35. (C)
36. (A) Tcos = mg
h
Tsin = m2 sin
n =
1 g
2 h
37. (C) T · V 0
because T is always to v.
Assertion and Reason
38. (B) 39. (C)
Passsage
40. (D) r = 2m
=
2
2
= 1 rad/sec.
= t
Vx = –Vsint
= –Vsin t
41. (B) ax = –
2
V
cos t
r
= –
2
V
cost
r
42. (C)
cm
L 3L
2m m
2 2
y
3m
=
5
6
L
From linear momentum conservation
(2m) V = (3m) Vcm
Vcm =
2
3
V ..............(1)
From angular momentum conservation (about 0)
L
3
2mV = Icmcm
=
2 2
2 2
cm
mL 2 L 2
m L 2m 2m L
12 3 12 3
cm =
8 V
11 L
43. (A) Velocity of A
A = cm – cm
7
L
6
](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-16-638.jpg)
![SOLUTION [CIRCULAR MOTION]
(62)
=
2
3
–
8
11 L
7
L
6
;
=
2 28
3 33
A =
2
11
44. (B) The speeds given to 2m will also be possessed by m
KE in horizontal position gets converted in PE in vertical
position.
1
2
2mv2
+
1
2
mv2
= change in PE in vertical position.
PE = 2 mg [ cos 30° – cos 60°] + mg [ cos 30° +
2
]
2 mg
3 3
mg
2 2 2 2
2m
m
3 1
mg [ 3 1] mg
2
=
3 1
mg 3 1
2 2
=
3 3 1
mg
2 2
K.E. =
1
2
3mv2
= mg
3 3 1
2
v =
3 3 1
g
2
45. (D) Both the masses will have same acceleration all the
time.
Their velocities and distance covered will be same.
46. (A) Length of spring at maximum = 2 cos
Extension is x = (2 cos – )
Now initial potential energy of the spring is converted into
final PE of spring and gravitational PE.
1
2
k2
=
1
2
k (2 cos – )2
+ mg ( – cos )
Putting values
1
2
× 10 × 12
=
1
2
× 10 (2 cos – 1)2
+ 10 (1 – cos )
5 = 5 (2 cos – 1)2
+ 10 – 10 cos
2 cos
m
q
1 = (2 cos – 1)2
+ 2 – 2 cos
2 cos – 1 = (2 cos – 1)2
cos =
1
2
= 60°
Multiple Choice Questions
47. (B, C)
48. (A, C, D)
49. (B, D) Velocity of point object w.r.t. hemispherical body
V'
will be same in magnitude to that of weight of hemispherical
body. Hence, for total velocity p
V
which is the resultant of V
& V'
we have Vp =
2 2 2
V V 2V cos 120
= V
acceleration of p = acc. of p w.r.t.
hemispherical body + acc. of hemispherical body
= t
'
p
a
+ n
'
p
a
+ a
where '
p
a
is acceleration of 'p' w.r.t. hemispherical body &
t
'
p
a
& n
'
p
a
the tangential & normal component in
corresponding circular motion.
Here t
'
p
a
= a
& n
'
p
a
=
2
p
V
R
Hence ap =
2
2
2
0
P
V
acos30 a acos60
R
=
2 2
2
V a 3 a
R 2 2
50. (B, C, D) 2
F
w = F2
2
OP = 30 · (6) = 180 J
3
F
w =
2
1
P
3
P
Along the path
F dx
=
2 6
4
3
0
F dx
= 15 · (3) = 45J
1
F
w =
2
1
P
11
P
F dx
1
F
w =
/ 2
0
20 cos Rd
4 2
1
F
w = 20 (–2) R ·
/ 2
0
sin
4 2
1
F
w = (–40) · 6 0 sin
4
](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-17-638.jpg)
![SOLUTION [CIRCULAR MOTION]
(63)
1
F
w = 120 2 J
Work done by F1 is independent of path. So it is conservative in
nature
51. (A,C) 52. (A)
53. (A,D) 54. (A,B)
55. (A,B,C) 2
E
V = V2 + 2g(R – R cos 60°)
4gr = V2 + gR
V = 3gR
2
B
V = 2
E
V – 2gR = 2gR
N =
2
P
mV
R
= 2mg
NE mg =
2
E
mV
R
NE = 5mg]
56. (A-q; B-r; C-r; D-q)
57. (A-r; B-s; C-p; D-q)
58. The motion of the motor car over a convex bridge AB is the
motion along the segment of a circle AB (Figure;
The centripetal force is provided by the difference of weight mg
of the car and the normal reaction R of the bridge.
mg – R =
2
mv
r
or R = mg –
2
mv
r
Clearly R < mg, i.e., the weight of the moving car is less than the
weight of the stationary car.
59. (a) v0/3, (b) 3 5gR
(a) Conserving momentum in horizontal direction
mv0 = (2m + m)v, v =
0
v
3
Collision is perfectly inelastic
(b) Now 3 m mass will move in the circle and 3 m mass requires
5Rg minimum velocity at bottom most point to execute the
loop so
V =
0
V
3
= 5Rg , then v0 = 3 5Rg
60. tn–1
Given radial acceleration
ar = ktn =
2
v
R
v2 = Rktn v = Rk tn/2
dv
dt
=
n
Rk
2
n
1
2
t
Tangential force, Ft = m
dv
dt
= m
n
2 Rk
n
1
2
t
Power developed = v
·
F
=
r t t
F F ·v F v
= m
n
2 Rk
n
1
2
t
·
n / 2
Rk t =
n 1
mnRk
t
2
P tn–1
61. net
19(0.2) – 12(0.05)
= 3.8 – 0.6
= 3.2 N mt = 32
= 0.1 rad/s2
= 0
+ t
= 10 + (0.1) (10)
= 11 rad/s
62. FBD of block (Ref. sphere)
here for = 5 rad/s
mg sin60 > Fp
cos600
block will have
tendency to move
down along inclined
friction will be directed upward
x-axis Nsin60 – Ncos60 = m2
Rsin60
.............(1)
y-axis Ncos60 – Nsin60 = mg
.............(2)
From (1) and (2)
=
3 3
23
63. Le the speed of the particle after time t from starting be v
The centripetal acceleration
2
2
r
v
a r
r
& the corresponding angular speed t
.
2 2 2
r
a r( t) r t
...(i)
We known that the tangential acceleration
r
at ...(ii)
Since, t
r a
a (given)
2 2
r t r
1
t
64. As at the time of firing of the shell, the particle was at C and the
shell collides with it at B, therefore the number of the revolutions
completed by the particle is odd multiple of half i.e., (2n – 1)/2,
where n is an integer.
Let T be the time period of the particle, then
2 r 2 3.14 20
T 4second
v 31.4
If t be the time of the flight of the shell, then
t = time of [(2n – 1)/2] revolutions of the particle](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-18-638.jpg)
![SOLUTION [CIRCULAR MOTION]
(64)
(2n 1)
4 2(2n 1)
2
second
for a projectile, the time of flight is given by
2usin
t
g
Hence,
2usin
2(2n 1)
g
...(i)
The range of the projectile is given by
2
u sin2
R
g
Hence,
2
u sin2
20 3
g
...(ii)
From equation (i) and (ii)
2
(2n 1)
tan
3
For to be smallest, n = 1, so
2
(2n 1)
tan
3
65. (0015) Let the angular velocity of rod at the time of collision be
w
According to the law of conservation of energy
For the rod at the horizontal and vertical positions, we get
m2gR =
2
R
g
m
I
2
1 2
2
2
gR
m2
=
2
2
2
·
3
R
m
2
1
= =
R
g
3
Applying the law of conservation of angular momentum about
P
Let the angular speed of block about P after the collision be 0.
I = m1R20
3
R
m 2
2
= m1R20 0 =
R
g
3
m
3
m
1
2
Linear velocity of ball is
v0 = 0R v0 = gR
3
m
3
m
1
2
For ball to complete the circle
v0 = gR
5 = gR
3
m
3
m
1
2
1
2
m
m
= 15 ]
66. (0024 )
A
2 r
2 r
v = 4 r
rel
67. (0012)
T
T
N
2T – N = m2Rcm = µ × R ×
2
R
V
×
R
2
2T – N = 2µv2
N = 2T – 2µv2 = 2 × 10 – 2 × 1 × 4 = 12 N ]](https://image.slidesharecdn.com/04-220507091540-a06aac3c/95/Circular-Motion-JEE-Advanced-Important-Questions-19-638.jpg)