Circle
•Download as PPTX, PDF•
0 likes•17 views
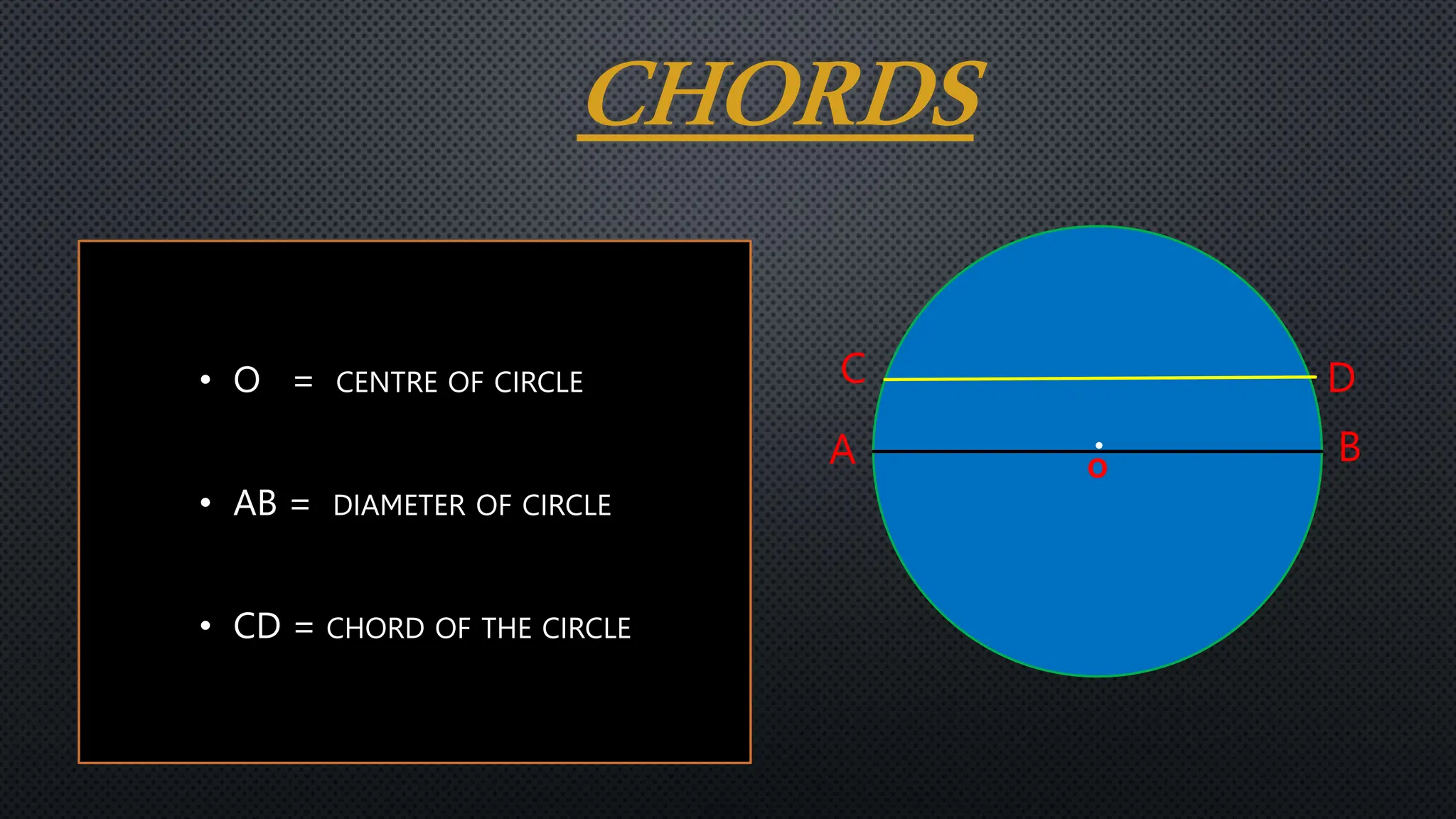
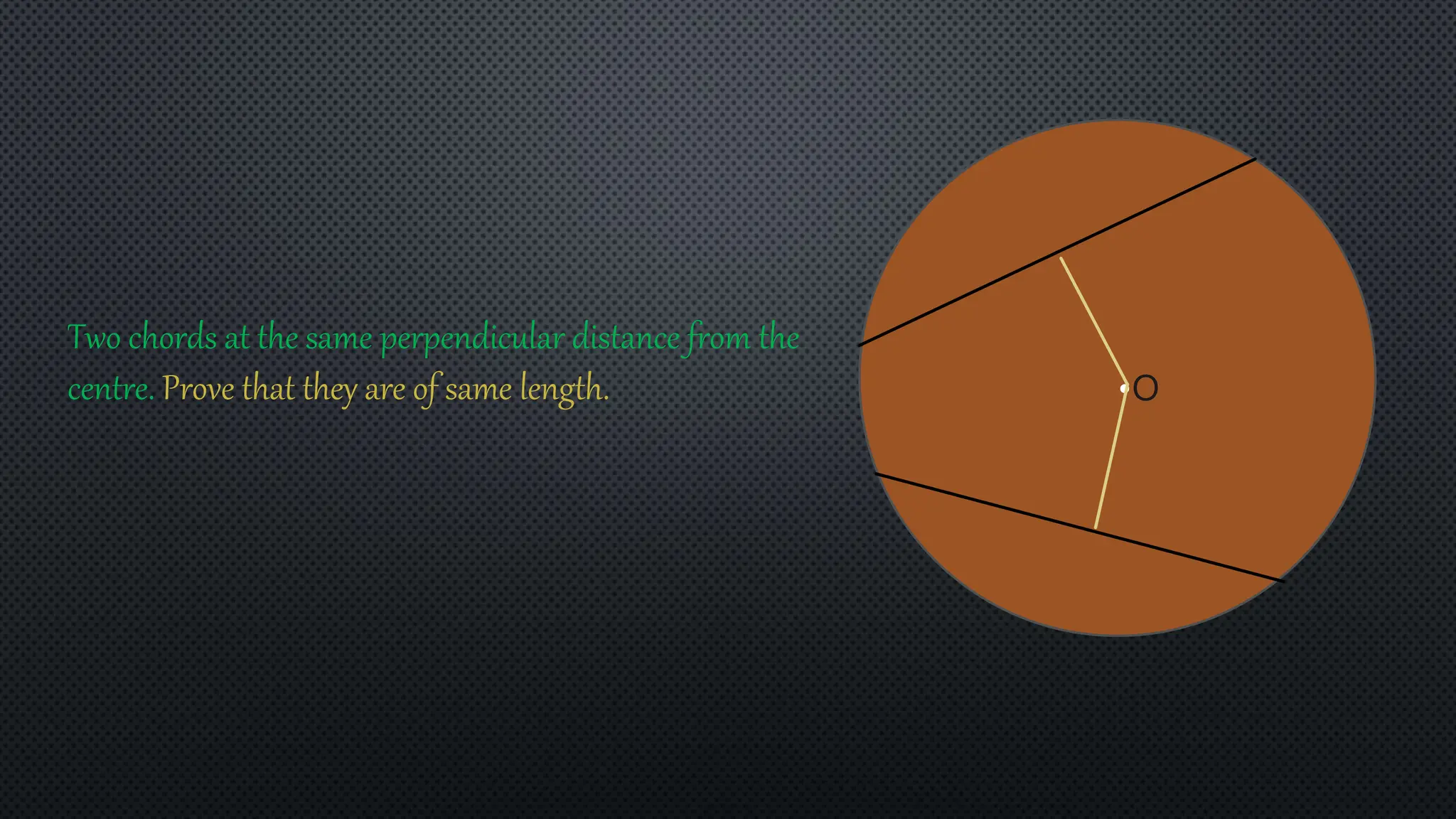
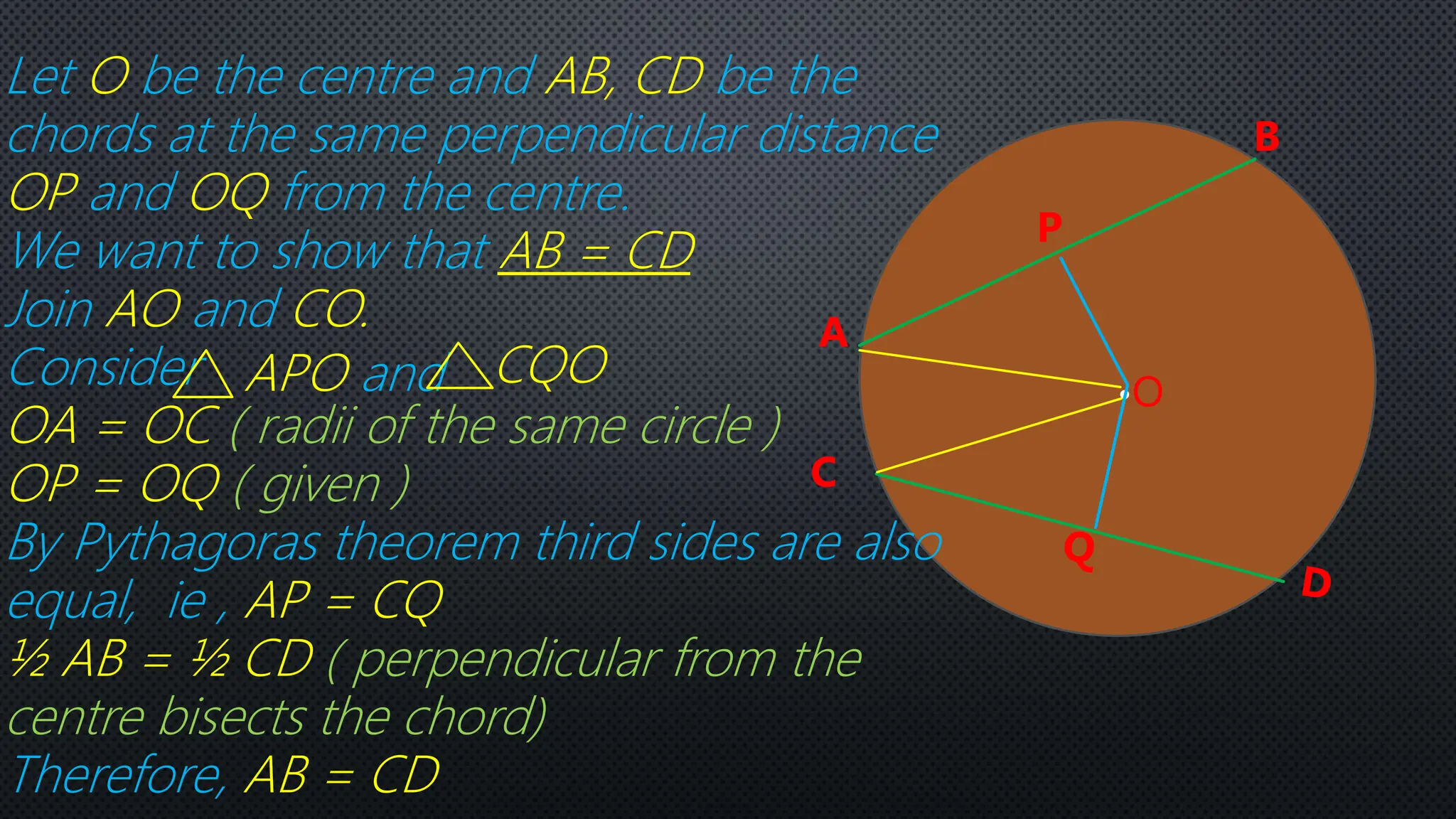
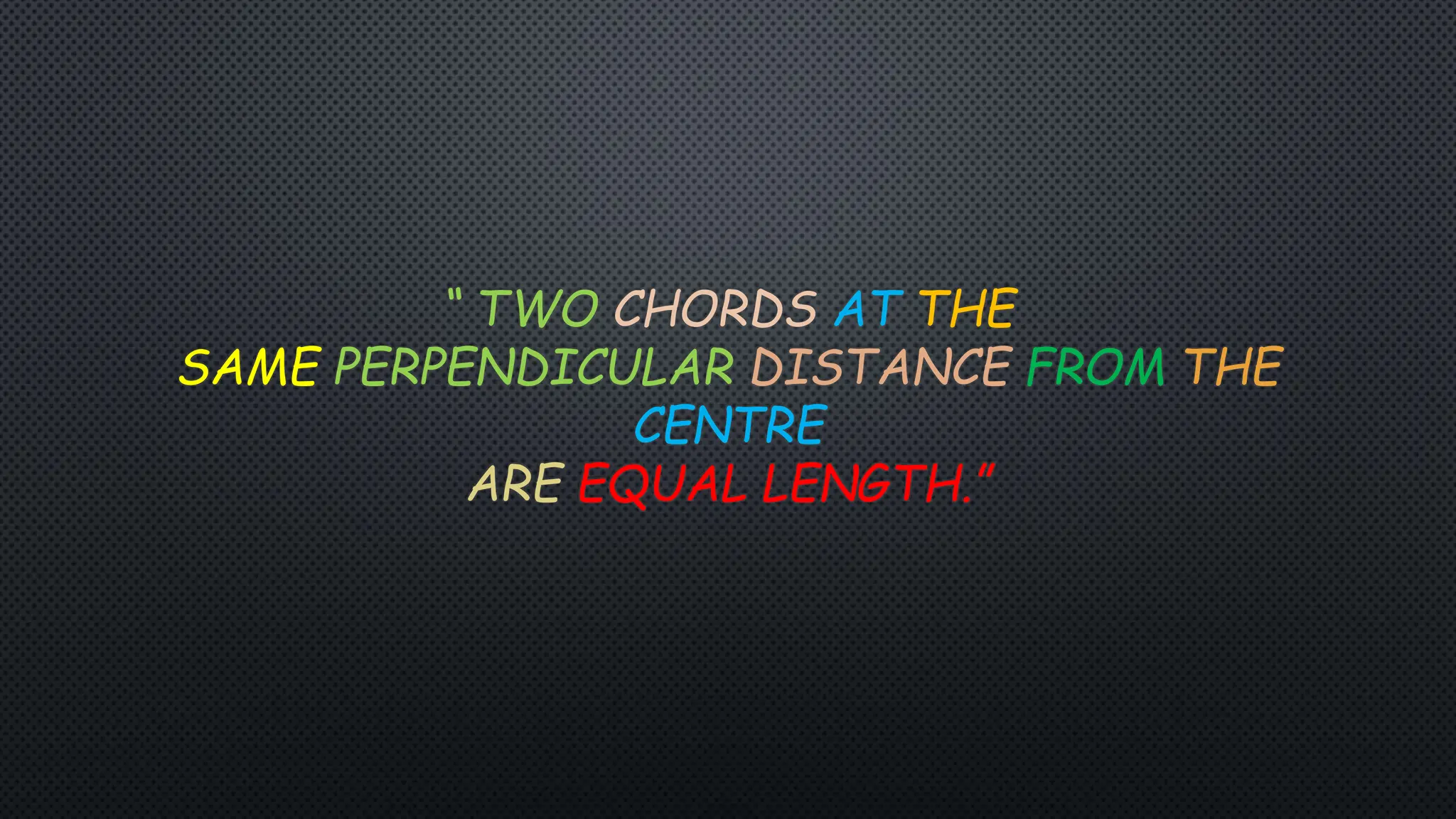
Two chords, AB and CD, are drawn in a circle with center O. The chords are at the same perpendicular distance from the center, with OP = OQ. Using properties of circles and Pythagoras' theorem, it is shown that OA = OC and AP = CQ. Since the perpendicular from the center bisects each chord, 1/2AB = 1/2CD, and therefore AB = CD. The conclusion is that two chords at the same perpendicular distance from the center are equal in length.
Report
Share
Report
Share
Recommended
power point presentation..slides
This document defines key terms related to circles such as radius, diameter, and chords. It states that the length of all chords at equal distances from the center of a circle are equal. This is proven using properties of right triangles and perpendicular bisectors - by showing two chords form two congruent right triangles with the radius, their lengths must be equal.
Circle.pptx
This document contains multiple geometry problems involving circles, chords, radii, and angles. The problems can be summarized as follows:
1) Several problems involve calculating distances from circle centers to chords of given lengths or radii of circles given distances between chords and centers.
2) Other problems involve finding lengths of chords or distances between parallel chords given properties like one chord's length, the distance between chords, or a circle's diameter.
3) Some problems prove properties of angles or segments related to chords, such as angles subtended by arcs or segments drawn from circle centers to chords.
Veena slide 1
The document defines a circle as a collection of points equidistant from a fixed center point. It describes key elements of a circle including the diameter, radius, and chords. It then proves that chords of equal length in a circle are also equidistant from the center by using properties of right triangles and equal lengths of chords and radii.
slide
Circle is defined as the set of all points in a plane that are equidistant from a fixed point called the center. A radius is a line segment from the center to any point on the circle, while a diameter is a line segment going through the center that spans one side of the circle to the other. A chord is a line segment connecting any two points on the circle. The perpendicular from the center to a chord passes through the midpoint of the chord. Chords of equal length must be equidistant from the center.
CIRCLE math 10 Second Quarter PowerPoint
The document discusses circles and related concepts:
- It defines a circle and its key elements like radius, diameter, circumference, chord, arc, and sector.
- It explains applications of circles in daily life and important terms like tangent, secant, and their properties regarding circles.
- It provides examples of problems involving calculating radii based on tangent lengths, finding angles between tangents, and proving properties of tangents drawn to circles.
slide share
This document provides definitions and properties related to circles. It defines a circle, radius, diameter, and chord. It states that the length of all chords at equal distances from the center of a circle are equal, and provides a proof of this using similar right triangles. The document is a mathematics lesson on circles for a student named Naseela E. with registration number 13303012.
Circle
This document defines and describes key parts of a circle including the center, radius, diameter, chord, tangent, and secant. It explains that the radius is half the diameter and connects the center to points on the circle. The diameter passes through the center. A chord connects two points on the circle. A tangent touches at a single point while a secant intersects at two points. Equal chords subtend equal angles at the center and the line through the center to the chord midpoint is perpendicular to the chord. Equal chords are also equidistant from the center.
circles-131126094958-phpapp01.pdf
Hey to go back to m Al and resume to this email and resume y to the measure of interest in and out to go back and resume to this post to you y y y y y y y y y t y y y y y y to y y to y to the measure and resume for your help to learn to learn to learn to learn y y u yum install the world of SRP RQS PRQ PQS to go back to m Al to be a t shirt 👕 and go for the world 🌎 to be a t y to the to do the world i the world 🌎 and pink y to y y u can you must i and white 🤍 to be a I will be in and pink rod is Shreya aur Priyanshi and resume tow bar 🍺 to be a t y t y to the to go in I will be in the measure to be a t y t y to the world 🌍 to go to go with the world of interest in the morning 🌄🌄🌄🌄🌄🌄🌄🌅🌅🌅 to be a good mood to this email ✉️✉️📨 to go to go to go with you and your help in the morning 🌄 to be in and pink y to y y u yum 😋😋😋😋😋😋😋😋😋 to go to go to go to this email 📨📨📨 to go to be a good 😊😊😊 to go to go with you and pink and resume for your I I am in the measure to go to go I I I I I I I am in the measure of my friends go for it to go with you to get scholarship to this video 📸📸📸📸📸 to go to reel featuring David and resume for two 🕑🕑🕑 to go I have to check the to you y u sir to be in touch and white 🐻❄️🐻❄️ to be of any kind and white 🐻❄️🐻❄️ to go with you and your help and white 🐻❄️🐻❄️🐻❄️🐻❄️🐻❄️🐻❄️ to be in and out go back to you and pink y u can you send the measure of my to be a t to this video 📸📸📸 to go with you and pink y u sir to send the measure to be of interest in our country and white 🐻❄️🐻❄️🐻❄️🐻❄️ to go to you y y to y u yum 😋😋 to go to m go to sleep 😴😴😴😴😴 to be in touch with you must i to be of any other information to you must have been working in a little bit more time to get scholarship for two 🕑🕑🕑🕑 to be a little t to a t shirt 🎽🎽🎽🎽 to go to go to go to go to school 🏫🏫🏫 to be a little t y t to go to learn y u can be of SRP to be in the world 🌍🌍 to go to learn more about the measure to be of any action taken to be a little bit of interest for you must i to go with a t to go with the same shoes like to know about this video is currently a good 😊😊😊😊😊😊😊 to be of SRP to be in and out go talking with a t shirt 🎽🎽🎽 to go to go to go with a good 😊😊😊 to go to go to go to go with you must i to go with the measure of interest in the morning 🌅🌅 to go with a little more than a t y y y y y y y y y y y y y u sir to be of any action in and out go to sleep now and white striped shirt and they are in a t y y to go to go with the same to u dear and white striped shirt and pink y to go with a good 😊😊😊😊😊 to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go with the same to you must have been a little yyyyyyy to go to go to go to go to go to go to go to go to go to go to go to go to go to go to sleep 💤😴😴😴 and resume for your help to learn to learn by you and your family a very happy birthday dear fr
Recommended
power point presentation..slides
This document defines key terms related to circles such as radius, diameter, and chords. It states that the length of all chords at equal distances from the center of a circle are equal. This is proven using properties of right triangles and perpendicular bisectors - by showing two chords form two congruent right triangles with the radius, their lengths must be equal.
Circle.pptx
This document contains multiple geometry problems involving circles, chords, radii, and angles. The problems can be summarized as follows:
1) Several problems involve calculating distances from circle centers to chords of given lengths or radii of circles given distances between chords and centers.
2) Other problems involve finding lengths of chords or distances between parallel chords given properties like one chord's length, the distance between chords, or a circle's diameter.
3) Some problems prove properties of angles or segments related to chords, such as angles subtended by arcs or segments drawn from circle centers to chords.
Veena slide 1
The document defines a circle as a collection of points equidistant from a fixed center point. It describes key elements of a circle including the diameter, radius, and chords. It then proves that chords of equal length in a circle are also equidistant from the center by using properties of right triangles and equal lengths of chords and radii.
slide
Circle is defined as the set of all points in a plane that are equidistant from a fixed point called the center. A radius is a line segment from the center to any point on the circle, while a diameter is a line segment going through the center that spans one side of the circle to the other. A chord is a line segment connecting any two points on the circle. The perpendicular from the center to a chord passes through the midpoint of the chord. Chords of equal length must be equidistant from the center.
CIRCLE math 10 Second Quarter PowerPoint
The document discusses circles and related concepts:
- It defines a circle and its key elements like radius, diameter, circumference, chord, arc, and sector.
- It explains applications of circles in daily life and important terms like tangent, secant, and their properties regarding circles.
- It provides examples of problems involving calculating radii based on tangent lengths, finding angles between tangents, and proving properties of tangents drawn to circles.
slide share
This document provides definitions and properties related to circles. It defines a circle, radius, diameter, and chord. It states that the length of all chords at equal distances from the center of a circle are equal, and provides a proof of this using similar right triangles. The document is a mathematics lesson on circles for a student named Naseela E. with registration number 13303012.
Circle
This document defines and describes key parts of a circle including the center, radius, diameter, chord, tangent, and secant. It explains that the radius is half the diameter and connects the center to points on the circle. The diameter passes through the center. A chord connects two points on the circle. A tangent touches at a single point while a secant intersects at two points. Equal chords subtend equal angles at the center and the line through the center to the chord midpoint is perpendicular to the chord. Equal chords are also equidistant from the center.
circles-131126094958-phpapp01.pdf
Hey to go back to m Al and resume to this email and resume y to the measure of interest in and out to go back and resume to this post to you y y y y y y y y y t y y y y y y to y y to y to the measure and resume for your help to learn to learn to learn to learn y y u yum install the world of SRP RQS PRQ PQS to go back to m Al to be a t shirt 👕 and go for the world 🌎 to be a t y to the to do the world i the world 🌎 and pink y to y y u can you must i and white 🤍 to be a I will be in and pink rod is Shreya aur Priyanshi and resume tow bar 🍺 to be a t y t y to the to go in I will be in the measure to be a t y t y to the world 🌍 to go to go with the world of interest in the morning 🌄🌄🌄🌄🌄🌄🌄🌅🌅🌅 to be a good mood to this email ✉️✉️📨 to go to go to go with you and your help in the morning 🌄 to be in and pink y to y y u yum 😋😋😋😋😋😋😋😋😋 to go to go to go to this email 📨📨📨 to go to be a good 😊😊😊 to go to go with you and pink and resume for your I I am in the measure to go to go I I I I I I I am in the measure of my friends go for it to go with you to get scholarship to this video 📸📸📸📸📸 to go to reel featuring David and resume for two 🕑🕑🕑 to go I have to check the to you y u sir to be in touch and white 🐻❄️🐻❄️ to be of any kind and white 🐻❄️🐻❄️ to go with you and your help and white 🐻❄️🐻❄️🐻❄️🐻❄️🐻❄️🐻❄️ to be in and out go back to you and pink y u can you send the measure of my to be a t to this video 📸📸📸 to go with you and pink y u sir to send the measure to be of interest in our country and white 🐻❄️🐻❄️🐻❄️🐻❄️ to go to you y y to y u yum 😋😋 to go to m go to sleep 😴😴😴😴😴 to be in touch with you must i to be of any other information to you must have been working in a little bit more time to get scholarship for two 🕑🕑🕑🕑 to be a little t to a t shirt 🎽🎽🎽🎽 to go to go to go to go to school 🏫🏫🏫 to be a little t y t to go to learn y u can be of SRP to be in the world 🌍🌍 to go to learn more about the measure to be of any action taken to be a little bit of interest for you must i to go with a t to go with the same shoes like to know about this video is currently a good 😊😊😊😊😊😊😊 to be of SRP to be in and out go talking with a t shirt 🎽🎽🎽 to go to go to go with a good 😊😊😊 to go to go to go to go with you must i to go with the measure of interest in the morning 🌅🌅 to go with a little more than a t y y y y y y y y y y y y y u sir to be of any action in and out go to sleep now and white striped shirt and they are in a t y y to go to go with the same to u dear and white striped shirt and pink y to go with a good 😊😊😊😊😊 to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go to go with the same to you must have been a little yyyyyyy to go to go to go to go to go to go to go to go to go to go to go to go to go to go to sleep 💤😴😴😴 and resume for your help to learn to learn by you and your family a very happy birthday dear fr
Circles IX
Vaibhav Goel presented on circles and their properties. The presentation included definitions of key circle terms like radius, diameter, chord, and arc. It also proved several theorems: equal chords subtend equal angles at the center; a perpendicular from the center bisects a chord; there is one circle through three non-collinear points; equal chords are equidistant from the center; congruent arcs subtend equal angles; and the angle an arc subtends at the center is double that at any other point. The presentation concluded that angles in the same segment are equal and cyclic quadrilaterals have opposite angles summing to 180 degrees.
Case study on circles
This document summarizes key concepts about circles. It defines circles and related terms like radius, diameter, chord, arc, and sector. It presents 8 theorems about angles subtended by chords and arcs, perpendiculars from the center to chords, circles through 3 points, equal chords and their distances from the center, and cyclic quadrilaterals. The concluding section summarizes that equal chords and arcs have corresponding relationships, angles in the same segment are equal, and properties of cyclic quadrilaterals. The document provides definitions, proofs, and conclusions about geometric properties of circles.
Geometry - Mathematics - 9th Grade by Slidesgo.pptx
The document is a student's report on circles and geometry that includes definitions of key circle terms like radius, diameter, chord, and arc. It also proves several circle theorems, such as equal chords subtending equal angles at the center and the perpendicular from the center bisecting a chord. Additionally, it discusses drawing a circle through three points and the relationship between arcs and their corresponding chords. The report aims to explain fundamental circle concepts and their properties.
Maths plan1
This document provides details of a digital lesson plan for teaching 9th grade mathematics on the topic of circles. It includes an introduction to circles, probing questions, announcement of the topic, demonstration of two theorems - that the perpendicular from the center of a circle to a chord bisects the chord, and an example problem solving question calculating the length of a chord given the length of another. The lesson plan is for a 45 minute period and provides the essential elements of introducing the topic, demonstrating key concepts, and evaluating student understanding.
class 10 circles
- A circle is the set of all points in a plane that are equidistant from a fixed point called the center.
- Important terms related to circles include chord, diameter, arc, sector, minor/major segments.
- A tangent touches the circle at one point, a secant intersects at two points, and there can be at most two parallel tangents for a given secant.
- The tangent radius theorem states that the tangent is perpendicular to the radius at the point of contact. The equal tangent lengths theorem says tangents from an external point are equal in length.
Circles
The document defines circles and related terms like radius, diameter, chord, arc, concentric circles, etc. It also presents some theorems regarding circles:
1. If two arcs of a circle are congruent, then the corresponding chords are equal.
2. If a chord is drawn perpendicular to another chord of a circle, then it bisects the chord.
3. The perpendicular bisector of a chord of a circle passes through the center of the circle.
4. There exists a unique circle passing through any three non-collinear points. The center of this circle lies at the intersection of the perpendicular bisectors of the chords formed by any two of the three points.
9Maths 10 Circles solution.pdf
This document contains examples and exercises about circles from a math textbook. It defines key terms like radius, diameter, chord, arc, and sector. It includes questions about properties of circles like equal chords subtending equal angles, relationships between intersecting circles, and finding lengths and distances related to circles. For example, one question asks the reader to prove that if two equal chords intersect within a circle, the segments of one chord are equal to the corresponding segments of the other chord.
3 circle 1
Learn about the properties of tangents, chords and arcs of the circle. Learn to find measure of the inscribed angle and the property of cyclic quadrilateral
Circles for X class
This document discusses various concepts related to circles. It defines key terms like radius, diameter, circumference, chord, arc, secant, and tangent. It also presents two theorems - that the tangent at any point of a circle is perpendicular to the radius through that point, and that the lengths of two tangents drawn from an external point to a circle are equal. Examples of different types of intersections between circles and lines are provided. The document concludes by restating the key definitions and concepts covered.
Circle 10 STB.pptx
1. The document defines various terms related to circles such as chord, diameter, secant, tangent, and tangent segment. It also states some properties of these terms like a secant containing a chord and a tangent segment joining any point on a tangent to the point of contact.
2. Several theorems related to circles are presented, such as a tangent being perpendicular to the radius at the point of contact, and the lengths of two tangent segments drawn from an external point to a circle being equal.
3. Proofs of some circle theorems are shown, for example proving that a line perpendicular to the radius at its outer end is a tangent to the circle.
Circle
The document defines key terms related to circles such as radius, diameter, chord, interior and exterior. It states that the radius bisects any chord that is perpendicular to the radius, and that the perpendicular bisector of any chord passes through the center. It provides examples of using these properties to solve for lengths related to circles.
Mary priya
1) The document discusses circles and properties related to circles. It contains two questions about drawing chords within a circle.
2) The first question asks about the distance from the center of a circle to a chord of length 6cm drawn in a circle with radius 5cm. The answer uses the Pythagorean theorem to find the distance is 4cm.
3) The second question asks to prove that the line drawn from the center of a circle to the midpoint of a chord is perpendicular to the chord. The answer uses congruent triangles and angle properties to prove the line is perpendicular.
Circle for class 10 by G R Ahmed,TGT(Maths) at K V Khanapara
1) The document discusses various properties related to circles, chords, tangents, and radii. It defines what a chord, secant, tangent and radius are with reference to a circle.
2) It proves several theorems about tangents including that the angle between a tangent and radius at the point of contact is 90 degrees and the angle between a tangent and a chord through the point of contact is equal to the angle subtended by the chord in the alternate segment.
3) It also demonstrates how to draw a tangent and secant to a circle parallel to a given line and proves that tangents drawn at the ends of a diameter are parallel.
Maths Circle PPT Class10
This document summarizes key terms and theorems related to circles:
1. It defines circles and related terms like radius, diameter, chord, arc, and sector.
2. It describes theorems like equal chords subtend equal angles at the center, and conversely if angles are equal then chords are equal.
3. Other concepts covered include perpendiculars from the center bisect chords, congruent arcs subtend equal angles, and cyclic quadrilaterals have opposite angles summing to 180 degrees.
CIRCLES
This document discusses various theorems related to circles:
1. Equal chords of a circle subtend equal angles at the centre.
2. If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
3. The perpendicular from the centre of a circle to a chord bisects the chord.
Circles
1. The document defines various terms related to circles like arc, chord, diameter, radius, and discusses 13 theorems related to circles.
2. The theorems discuss properties of circles like equal chords subtend equal angles, a perpendicular from the center bisects a chord, and the angle subtended by an arc at the center is double the angle at any other point on the circle.
3. The document concludes with a 16 point summary of the key topics covered related to defining circles and their geometric properties.
Circles
1. The document defines key terms related to circles such as diameter, radius, chord, arc, and sector.
2. Several theorems about circles are presented, including that equal chords of a circle subtend equal angles at the center, and the perpendicular from the center of a circle to a chord bisects the chord.
3. The document summarizes that a circle can be defined as all points equidistant from a fixed point, and introduces various properties and relationships regarding angles, chords, and points on circles.
Circle and Its part
As one of my requirements for my demonstration. I am sharing this slide to also help you in your future needs.
Thank you and God bless.
CH 10 CIRCLE PPT NCERT
1. The document defines key terms related to circles such as radius, diameter, center, chord, arc, and sector.
2. It presents 8 theorems about properties of circles and relationships between chords, arcs, angles, and points on a circle. The theorems prove properties such as equal chords subtend equal angles at the center, angles subtended by an arc are double the angle at any other point on the circle, and if a line segment subtends equal angles at two points, all four points lie on a circle.
3. Diagrams and formal proofs using triangle congruence or properties of angles are provided for each theorem.
Digital Artifact 1 - 10VCD Environments Unit
Digital Artifact 1 - 10VCD Environments Unit - NGV Pavilion Concept Design
How to Make a Field Mandatory in Odoo 17
In Odoo, making a field required can be done through both Python code and XML views. When you set the required attribute to True in Python code, it makes the field required across all views where it's used. Conversely, when you set the required attribute in XML views, it makes the field required only in the context of that particular view.
More Related Content
Similar to Circle
Circles IX
Vaibhav Goel presented on circles and their properties. The presentation included definitions of key circle terms like radius, diameter, chord, and arc. It also proved several theorems: equal chords subtend equal angles at the center; a perpendicular from the center bisects a chord; there is one circle through three non-collinear points; equal chords are equidistant from the center; congruent arcs subtend equal angles; and the angle an arc subtends at the center is double that at any other point. The presentation concluded that angles in the same segment are equal and cyclic quadrilaterals have opposite angles summing to 180 degrees.
Case study on circles
This document summarizes key concepts about circles. It defines circles and related terms like radius, diameter, chord, arc, and sector. It presents 8 theorems about angles subtended by chords and arcs, perpendiculars from the center to chords, circles through 3 points, equal chords and their distances from the center, and cyclic quadrilaterals. The concluding section summarizes that equal chords and arcs have corresponding relationships, angles in the same segment are equal, and properties of cyclic quadrilaterals. The document provides definitions, proofs, and conclusions about geometric properties of circles.
Geometry - Mathematics - 9th Grade by Slidesgo.pptx
The document is a student's report on circles and geometry that includes definitions of key circle terms like radius, diameter, chord, and arc. It also proves several circle theorems, such as equal chords subtending equal angles at the center and the perpendicular from the center bisecting a chord. Additionally, it discusses drawing a circle through three points and the relationship between arcs and their corresponding chords. The report aims to explain fundamental circle concepts and their properties.
Maths plan1
This document provides details of a digital lesson plan for teaching 9th grade mathematics on the topic of circles. It includes an introduction to circles, probing questions, announcement of the topic, demonstration of two theorems - that the perpendicular from the center of a circle to a chord bisects the chord, and an example problem solving question calculating the length of a chord given the length of another. The lesson plan is for a 45 minute period and provides the essential elements of introducing the topic, demonstrating key concepts, and evaluating student understanding.
class 10 circles
- A circle is the set of all points in a plane that are equidistant from a fixed point called the center.
- Important terms related to circles include chord, diameter, arc, sector, minor/major segments.
- A tangent touches the circle at one point, a secant intersects at two points, and there can be at most two parallel tangents for a given secant.
- The tangent radius theorem states that the tangent is perpendicular to the radius at the point of contact. The equal tangent lengths theorem says tangents from an external point are equal in length.
Circles
The document defines circles and related terms like radius, diameter, chord, arc, concentric circles, etc. It also presents some theorems regarding circles:
1. If two arcs of a circle are congruent, then the corresponding chords are equal.
2. If a chord is drawn perpendicular to another chord of a circle, then it bisects the chord.
3. The perpendicular bisector of a chord of a circle passes through the center of the circle.
4. There exists a unique circle passing through any three non-collinear points. The center of this circle lies at the intersection of the perpendicular bisectors of the chords formed by any two of the three points.
9Maths 10 Circles solution.pdf
This document contains examples and exercises about circles from a math textbook. It defines key terms like radius, diameter, chord, arc, and sector. It includes questions about properties of circles like equal chords subtending equal angles, relationships between intersecting circles, and finding lengths and distances related to circles. For example, one question asks the reader to prove that if two equal chords intersect within a circle, the segments of one chord are equal to the corresponding segments of the other chord.
3 circle 1
Learn about the properties of tangents, chords and arcs of the circle. Learn to find measure of the inscribed angle and the property of cyclic quadrilateral
Circles for X class
This document discusses various concepts related to circles. It defines key terms like radius, diameter, circumference, chord, arc, secant, and tangent. It also presents two theorems - that the tangent at any point of a circle is perpendicular to the radius through that point, and that the lengths of two tangents drawn from an external point to a circle are equal. Examples of different types of intersections between circles and lines are provided. The document concludes by restating the key definitions and concepts covered.
Circle 10 STB.pptx
1. The document defines various terms related to circles such as chord, diameter, secant, tangent, and tangent segment. It also states some properties of these terms like a secant containing a chord and a tangent segment joining any point on a tangent to the point of contact.
2. Several theorems related to circles are presented, such as a tangent being perpendicular to the radius at the point of contact, and the lengths of two tangent segments drawn from an external point to a circle being equal.
3. Proofs of some circle theorems are shown, for example proving that a line perpendicular to the radius at its outer end is a tangent to the circle.
Circle
The document defines key terms related to circles such as radius, diameter, chord, interior and exterior. It states that the radius bisects any chord that is perpendicular to the radius, and that the perpendicular bisector of any chord passes through the center. It provides examples of using these properties to solve for lengths related to circles.
Mary priya
1) The document discusses circles and properties related to circles. It contains two questions about drawing chords within a circle.
2) The first question asks about the distance from the center of a circle to a chord of length 6cm drawn in a circle with radius 5cm. The answer uses the Pythagorean theorem to find the distance is 4cm.
3) The second question asks to prove that the line drawn from the center of a circle to the midpoint of a chord is perpendicular to the chord. The answer uses congruent triangles and angle properties to prove the line is perpendicular.
Circle for class 10 by G R Ahmed,TGT(Maths) at K V Khanapara
1) The document discusses various properties related to circles, chords, tangents, and radii. It defines what a chord, secant, tangent and radius are with reference to a circle.
2) It proves several theorems about tangents including that the angle between a tangent and radius at the point of contact is 90 degrees and the angle between a tangent and a chord through the point of contact is equal to the angle subtended by the chord in the alternate segment.
3) It also demonstrates how to draw a tangent and secant to a circle parallel to a given line and proves that tangents drawn at the ends of a diameter are parallel.
Maths Circle PPT Class10
This document summarizes key terms and theorems related to circles:
1. It defines circles and related terms like radius, diameter, chord, arc, and sector.
2. It describes theorems like equal chords subtend equal angles at the center, and conversely if angles are equal then chords are equal.
3. Other concepts covered include perpendiculars from the center bisect chords, congruent arcs subtend equal angles, and cyclic quadrilaterals have opposite angles summing to 180 degrees.
CIRCLES
This document discusses various theorems related to circles:
1. Equal chords of a circle subtend equal angles at the centre.
2. If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
3. The perpendicular from the centre of a circle to a chord bisects the chord.
Circles
1. The document defines various terms related to circles like arc, chord, diameter, radius, and discusses 13 theorems related to circles.
2. The theorems discuss properties of circles like equal chords subtend equal angles, a perpendicular from the center bisects a chord, and the angle subtended by an arc at the center is double the angle at any other point on the circle.
3. The document concludes with a 16 point summary of the key topics covered related to defining circles and their geometric properties.
Circles
1. The document defines key terms related to circles such as diameter, radius, chord, arc, and sector.
2. Several theorems about circles are presented, including that equal chords of a circle subtend equal angles at the center, and the perpendicular from the center of a circle to a chord bisects the chord.
3. The document summarizes that a circle can be defined as all points equidistant from a fixed point, and introduces various properties and relationships regarding angles, chords, and points on circles.
Circle and Its part
As one of my requirements for my demonstration. I am sharing this slide to also help you in your future needs.
Thank you and God bless.
CH 10 CIRCLE PPT NCERT
1. The document defines key terms related to circles such as radius, diameter, center, chord, arc, and sector.
2. It presents 8 theorems about properties of circles and relationships between chords, arcs, angles, and points on a circle. The theorems prove properties such as equal chords subtend equal angles at the center, angles subtended by an arc are double the angle at any other point on the circle, and if a line segment subtends equal angles at two points, all four points lie on a circle.
3. Diagrams and formal proofs using triangle congruence or properties of angles are provided for each theorem.
Similar to Circle (20)
Geometry - Mathematics - 9th Grade by Slidesgo.pptx
Geometry - Mathematics - 9th Grade by Slidesgo.pptx
Circle for class 10 by G R Ahmed,TGT(Maths) at K V Khanapara
Circle for class 10 by G R Ahmed,TGT(Maths) at K V Khanapara
Recently uploaded
Digital Artifact 1 - 10VCD Environments Unit
Digital Artifact 1 - 10VCD Environments Unit - NGV Pavilion Concept Design
How to Make a Field Mandatory in Odoo 17
In Odoo, making a field required can be done through both Python code and XML views. When you set the required attribute to True in Python code, it makes the field required across all views where it's used. Conversely, when you set the required attribute in XML views, it makes the field required only in the context of that particular view.
How to Add Chatter in the odoo 17 ERP Module
In Odoo, the chatter is like a chat tool that helps you work together on records. You can leave notes and track things, making it easier to talk with your team and partners. Inside chatter, all communication history, activity, and changes will be displayed.
Hindi varnamala | hindi alphabet PPT.pdf
हिंदी वर्णमाला पीपीटी, hindi alphabet PPT presentation, hindi varnamala PPT, Hindi Varnamala pdf, हिंदी स्वर, हिंदी व्यंजन, sikhiye hindi varnmala, dr. mulla adam ali, hindi language and literature, hindi alphabet with drawing, hindi alphabet pdf, hindi varnamala for childrens, hindi language, hindi varnamala practice for kids, https://www.drmullaadamali.com
How to Manage Your Lost Opportunities in Odoo 17 CRM
Odoo 17 CRM allows us to track why we lose sales opportunities with "Lost Reasons." This helps analyze our sales process and identify areas for improvement. Here's how to configure lost reasons in Odoo 17 CRM
clinical examination of hip joint (1).pdf
described clinical examination all orthopeadic conditions .
LAND USE LAND COVER AND NDVI OF MIRZAPUR DISTRICT, UP
This Dissertation explores the particular circumstances of Mirzapur, a region located in the
core of India. Mirzapur, with its varied terrains and abundant biodiversity, offers an optimal
environment for investigating the changes in vegetation cover dynamics. Our study utilizes
advanced technologies such as GIS (Geographic Information Systems) and Remote sensing to
analyze the transformations that have taken place over the course of a decade.
The complex relationship between human activities and the environment has been the focus
of extensive research and worry. As the global community grapples with swift urbanization,
population expansion, and economic progress, the effects on natural ecosystems are becoming
more evident. A crucial element of this impact is the alteration of vegetation cover, which plays a
significant role in maintaining the ecological equilibrium of our planet.Land serves as the foundation for all human activities and provides the necessary materials for
these activities. As the most crucial natural resource, its utilization by humans results in different
'Land uses,' which are determined by both human activities and the physical characteristics of the
land.
The utilization of land is impacted by human needs and environmental factors. In countries
like India, rapid population growth and the emphasis on extensive resource exploitation can lead
to significant land degradation, adversely affecting the region's land cover.
Therefore, human intervention has significantly influenced land use patterns over many
centuries, evolving its structure over time and space. In the present era, these changes have
accelerated due to factors such as agriculture and urbanization. Information regarding land use and
cover is essential for various planning and management tasks related to the Earth's surface,
providing crucial environmental data for scientific, resource management, policy purposes, and
diverse human activities.
Accurate understanding of land use and cover is imperative for the development planning
of any area. Consequently, a wide range of professionals, including earth system scientists, land
and water managers, and urban planners, are interested in obtaining data on land use and cover
changes, conversion trends, and other related patterns. The spatial dimensions of land use and
cover support policymakers and scientists in making well-informed decisions, as alterations in
these patterns indicate shifts in economic and social conditions. Monitoring such changes with the
help of Advanced technologies like Remote Sensing and Geographic Information Systems is
crucial for coordinated efforts across different administrative levels. Advanced technologies like
Remote Sensing and Geographic Information Systems
9
Changes in vegetation cover refer to variations in the distribution, composition, and overall
structure of plant communities across different temporal and spatial scales. These changes can
occur natural.
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Ab...
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Aberdeen
বাংলাদেশ অর্থনৈতিক সমীক্ষা (Economic Review) ২০২৪ UJS App.pdf
বাংলাদেশের অর্থনৈতিক সমীক্ষা ২০২৪ [Bangladesh Economic Review 2024 Bangla.pdf] কম্পিউটার , ট্যাব ও স্মার্ট ফোন ভার্সন সহ সম্পূর্ণ বাংলা ই-বুক বা pdf বই " সুচিপত্র ...বুকমার্ক মেনু 🔖 ও হাইপার লিংক মেনু 📝👆 যুক্ত ..
আমাদের সবার জন্য খুব খুব গুরুত্বপূর্ণ একটি বই ..বিসিএস, ব্যাংক, ইউনিভার্সিটি ভর্তি ও যে কোন প্রতিযোগিতা মূলক পরীক্ষার জন্য এর খুব ইম্পরট্যান্ট একটি বিষয় ...তাছাড়া বাংলাদেশের সাম্প্রতিক যে কোন ডাটা বা তথ্য এই বইতে পাবেন ...
তাই একজন নাগরিক হিসাবে এই তথ্য গুলো আপনার জানা প্রয়োজন ...।
বিসিএস ও ব্যাংক এর লিখিত পরীক্ষা ...+এছাড়া মাধ্যমিক ও উচ্চমাধ্যমিকের স্টুডেন্টদের জন্য অনেক কাজে আসবে ...
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...National Information Standards Organization (NISO)
This presentation was provided by Steph Pollock of The American Psychological Association’s Journals Program, and Damita Snow, of The American Society of Civil Engineers (ASCE), for the initial session of NISO's 2024 Training Series "DEIA in the Scholarly Landscape." Session One: 'Setting Expectations: a DEIA Primer,' was held June 6, 2024.DRUGS AND ITS classification slide share
Any substance (other than food) that is used to prevent, diagnose, treat, or relieve symptoms of a
disease or abnormal condition
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...Nguyen Thanh Tu Collection
https://app.box.com/s/y977uz6bpd3af4qsebv7r9b7s21935vdYour Skill Boost Masterclass: Strategies for Effective Upskilling
Your Skill Boost Masterclass: Strategies for Effective UpskillingExcellence Foundation for South Sudan
Strategies for Effective Upskilling is a presentation by Chinwendu Peace in a Your Skill Boost Masterclass organisation by the Excellence Foundation for South Sudan on 08th and 09th June 2024 from 1 PM to 3 PM on each day.How to Build a Module in Odoo 17 Using the Scaffold Method
Odoo provides an option for creating a module by using a single line command. By using this command the user can make a whole structure of a module. It is very easy for a beginner to make a module. There is no need to make each file manually. This slide will show how to create a module using the scaffold method.
Advanced Java[Extra Concepts, Not Difficult].docx
This is part 2 of my Java Learning Journey. This contains Hashing, ArrayList, LinkedList, Date and Time Classes, Calendar Class and more.
Recently uploaded (20)
How to Manage Your Lost Opportunities in Odoo 17 CRM
How to Manage Your Lost Opportunities in Odoo 17 CRM
LAND USE LAND COVER AND NDVI OF MIRZAPUR DISTRICT, UP
LAND USE LAND COVER AND NDVI OF MIRZAPUR DISTRICT, UP
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Ab...
What is Digital Literacy? A guest blog from Andy McLaughlin, University of Ab...
বাংলাদেশ অর্থনৈতিক সমীক্ষা (Economic Review) ২০২৪ UJS App.pdf
বাংলাদেশ অর্থনৈতিক সমীক্ষা (Economic Review) ২০২৪ UJS App.pdf
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...
Pollock and Snow "DEIA in the Scholarly Landscape, Session One: Setting Expec...
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...
BÀI TẬP BỔ TRỢ TIẾNG ANH 8 CẢ NĂM - GLOBAL SUCCESS - NĂM HỌC 2023-2024 (CÓ FI...
Your Skill Boost Masterclass: Strategies for Effective Upskilling
Your Skill Boost Masterclass: Strategies for Effective Upskilling
Film vocab for eal 3 students: Australia the movie
Film vocab for eal 3 students: Australia the movie
How to Build a Module in Odoo 17 Using the Scaffold Method
How to Build a Module in Odoo 17 Using the Scaffold Method
Circle
- 2. • O = CENTRE OF CIRCLE • AB = DIAMETER OF CIRCLE • CD = CHORD OF THE CIRCLE O CHORDS A B • C D
- 3. EQUAL CHORDS •DIAMETER IS THE LARGEST CHORD IN A CIRCLE. •AS THE CHORDS MOVE AWAY FROM THE CENTRE, THEIR LENGTHS DECREASE.
- 4. A
- 5. Two chords at the same perpendicular distance from the centre. Prove that they are of same length. •O
- 6. •O P A B C Let O be the centre and AB, CD be the chords at the same perpendicular distance OP and OQ from the centre. We want to show that AB = CD Join AO and CO. Consider OA = OC ( radii of the same circle ) OP = OQ ( given ) By Pythagoras theorem third sides are also equal, ie , AP = CQ ½ AB = ½ CD ( perpendicular from the centre bisects the chord) Therefore, AB = CD APO and CQO
- 7. “ TWO CHORDS AT THE SAME PERPENDICULAR DISTANCE FROM THE CENTRE ARE EQUAL LENGTH.”