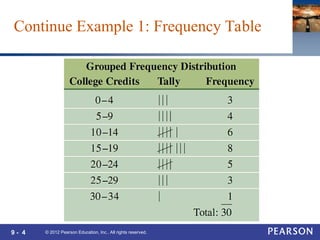
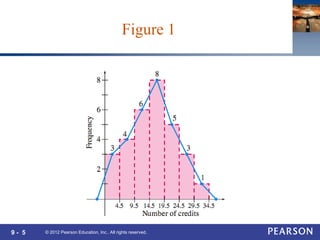
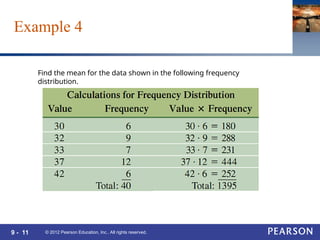
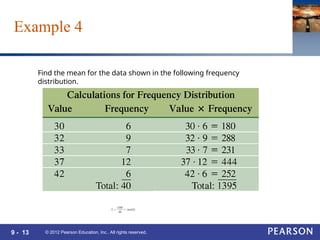
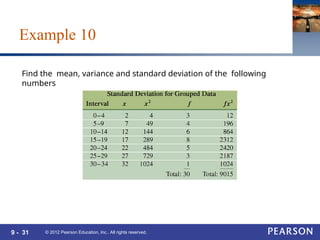
This document covers Chapter 9 of a statistics textbook, focusing on frequency distributions and measures of central tendency, including mean, median, and mode. It provides examples and exercises related to calculating these statistical measures from given data sets and frequency distributions. Additionally, it discusses measures of variation such as range, variance, and standard deviation.