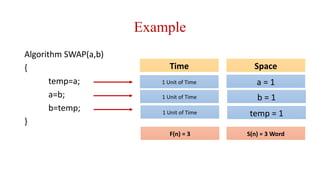
The document discusses algorithm learning outcomes with a focus on time and space complexity, definitions, and asymptotic analysis rules. It outlines how to evaluate an algorithm's performance based on the amount of memory required and the number of operations performed. Several example algorithms illustrate these concepts, including swap, sum, add, and multiply, alongside their respective time and space complexities.

1. Analysis OF Algorithm

2. Learning outcomes
• Space Complexity
• Time Complexity

3. Space Complexity
The amount of memory required by an algorithm to run to
completion
The term memory leaks refer to the amount of memory
required is larger than the memory available on a given
system
Fixed part: The size required to store certain data/variables,
that is independent of the size of the problem:
Such as int a (4 bytes)
Variable part: Space needed by variables, whose size is
dependent on the size of the problem:
Such as Dynamic List

4. Time Complexity
• the time complexity is the number of operations an
algorithm performs to complete its task.

5. Time Complexity vs Space Complexity

6. Asymptotic Analysis Rules
Rule 1: Only Consider the highest degree/rate of growth.
Example
N3
+ N2
+ 100
N3
Rule 2: Basic Math Operations ( + ,*,-,/) and assigning values to
variable takes constant time.
Example
x = x + 5
a = 5

7. Asymptotic Analysis Rules
Rule 3: Running time of the statement inside loop is the
number of iterations.
Example
For( i = 0 ; i < N ; i ++ )
{
N = N + 2
}
Time Complexity : C x N+1
Time Complexity : N
N+1
C

8. Asymptotic Analysis Rules
Rule 4: Nested Loop
Example
For( i = 0 ; i < N ; i ++ )
{
For( j = 0 ; j < N ; j ++ )
{
statements;
}
}
Time Complexity : (N+1) + [N x (N+1)] + C
Time Complexity : N2
N+1
N x (N+1)
C

9. Asymptotic Analysis Rules
Rule 5: Consecutive Statements (We add the Complexity of each statments).
Example
For( i = 0 ; i < N ; i ++ )
{
statements;
}
For( j = 0 ; j < N ; j ++ )
{
statements;
}
Time Complexity : (N+1) + C + (N+1) + C
Time Complexity : N
N+1
C
N+1
C

10. Algorithm SWAP(a,b)
{
temp=a;
a=b;
b=temp;
}
1 Unit of Time
1 Unit of Time
1 Unit of Time
F(n) = 3
Time Space
a = 1
b = 1
temp = 1
S(n) = 3 Word
Example

11. Example
Algorithm SUM(A,n)
{
S = 0;
for ( i = 0 ; i < n ; i ++)
{
S = S + A[ i ];
}
return S;
}
8 3 9 7 2
A
0 1 2 3 4
N = 5
1 N+1 N
i = 0
i = 1
i = 2
i = 3
i = 4
i = 5
Time Space
1 Unit of Time S = 1
N+1 Unit of Time N = 1
N Unit of Time A = N
1 Unit of Time i = 1
F(n) = 2N + 3 =N S(n) = N+3 =N Word

12. Example
Algorithm ADD( A, B, n)
{
for( i = 0 ; i <n ; i ++)
{
for( j = 0 ; j < n ; j ++)
{
C[ i ] [ j ]=A [ i ] [ j ] + B [ i ] [ j ];
}
}
}
Time Space
N+1
N
N
(N + 1)
N
A = N
B = N
C = N
i = 1
j = 1
n = 1
F(n) = 2N2
+ 2N +1 =N2
S(n) = 3N2
+ 3 =N2

13. Example
Algorithm MULTIPLY(A, B, n)
{
for(i = 0 ; i < n ; i++){
for(j = 0; j < n ; j++){
C[i , j] = 0;
for(k = 0; k < n ; k++){
C[i , j] = C[i , j] + A[i , k] * B [k, j];
}
}
}
}
Time Space
N+1
N N + 1
N N
N N N + 1
N N N
F(n)=2N3
+3N2
+2N+1=N3
A = N
B = N
C = N
N = 1
i = 1
j = 1
k = 1
F(n)=3N2
+4=N2

14. Thank You!!!