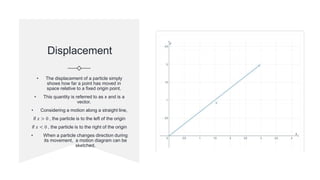
This document provides an overview of calculus-based kinematics. It defines the key terms of displacement, velocity, and acceleration. Displacement refers to how far an object has moved from a fixed point, velocity is the rate of change of displacement over time, and acceleration is the rate of change of velocity over time. The document provides examples of using calculus derivatives and integrals to derive kinematic equations for problems involving displacement, velocity, and acceleration functions.

1. CALCULUS-BASED
KINEMATICS
Prepared by: Engr. Idris Jeffrey M. Manguera

2. Intended
Learning
Outcome
At the end of this
lesson, the
student must be
able to:
• Define displacement,
velocity and
acceleration

3. Overview
Kinematics is a topic in
physics that describes the
motion of points, bodies and
systems in space.
Calculus can be used to
derive equations in
kinematics using derivatives
and their integrals.

4. What are the
kinematic
equations?
Displacement
Velocity
Acceleration

5. Displacement
• The displacement of a particle simply
shows how far a point has moved in
space relative to a fixed origin point.
• This quantity is referred to as x and is a
vector.
• Considering a motion along a straight line,
if 𝑥 > 0 , the particle is to the left of the origin
if 𝑥 < 0 , the particle is to the right of the origin
• When a particle changes direction during
its movement, a motion diagram can be
sketched.

6. Example:
An object travels with displacement function 𝑥 = 10𝑡2 − 7𝑡 + 1 meters, where 𝑡 > 0
seconds.
a) What is the initial displacement of the object?
b) What is the displacement after three seconds?

7. Velocity
• Velocity is how the displacement of the
particle changes with time or the rate of
change of displacement of the particle.
• Velocity will be referred to as v and 𝑣 =
𝑑𝑥
𝑑𝑡
. This means that if we have an
expression of x in terms of t, we take
the derivative of the expression to find
the velocity.
• The unit of velocity is 𝑚
𝑠 .
Example:
The displacement in meters of a car
moving between points A and B is given
by 𝑥 = 40𝑡2 − 15. Find an expression of
the velocity of the car at a given point in
time.

8. Acceleration
• Acceleration describes how much
faster or slower a particle becomes
over time. Acceleration is the rate of
change of velocity of a particle.
• Acceleration will be referred to as a
and a =
𝑑𝑣
𝑑𝑡
. But we know already that
𝑣 =
𝑑𝑥
𝑑𝑡
, so taking the second derivative
of the displacement x with respect to
time will give us the equation 𝑎 =
𝑑2𝑥
𝑑𝑡2.
• The unit of acceleration is 𝑚
𝑠2 .
Example:
The at time t of a bird is given by 𝑥 =
3𝑡2 + 12𝑡 − 5 m. What is the velocity and
acceleration of the bird?

9. THANK YOU!