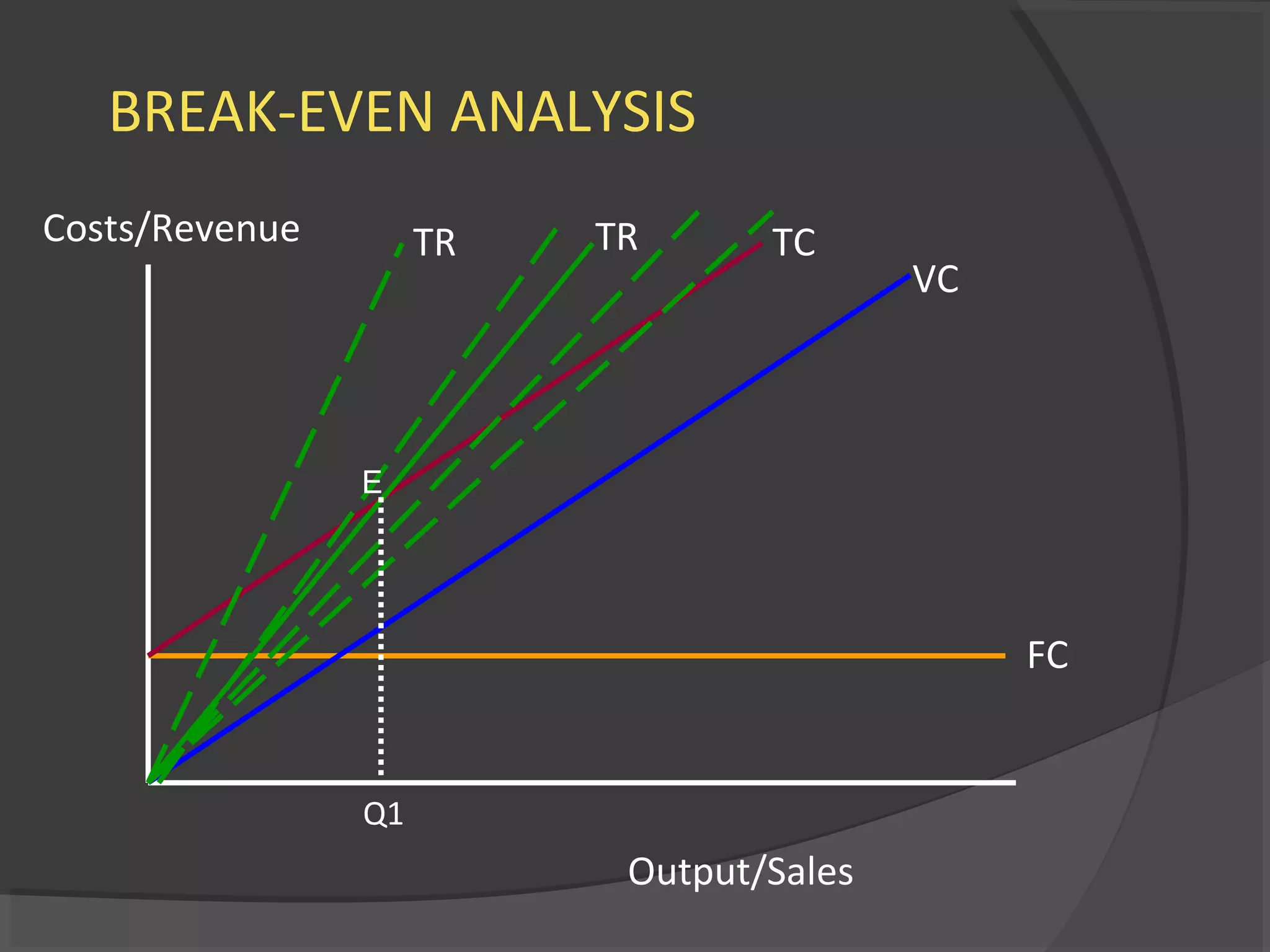
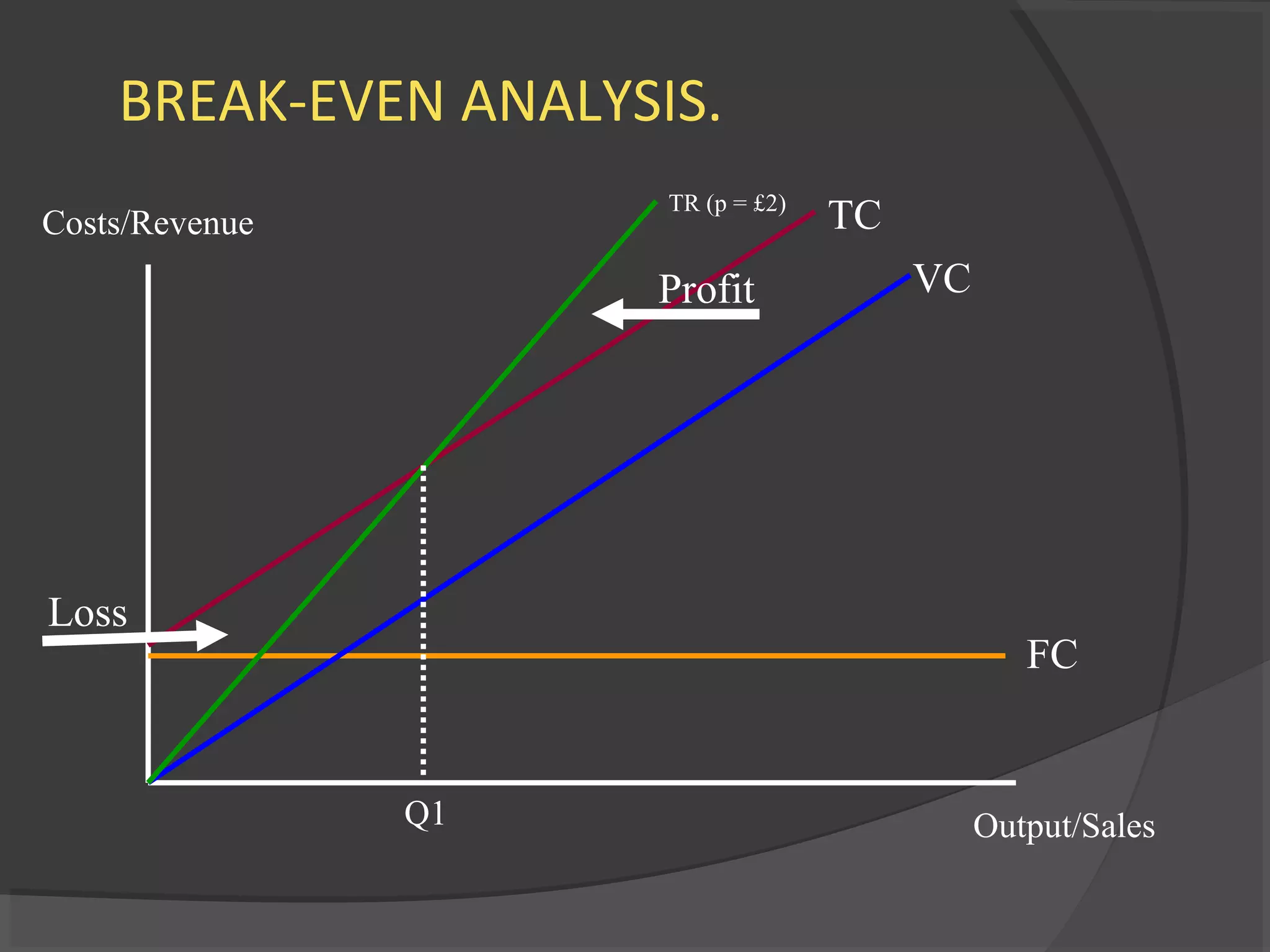
The document provides an overview of break-even analysis. It defines break-even point as the level of sales or production where total revenue equals total costs, resulting in no profit or loss. It explains fixed and variable costs and how to calculate break-even point algebraically as fixed costs divided by the difference between selling price and variable cost per unit. An example calculates that a company needs to sell 10,000 Christmas trees at $8 each to cover its $30,000 in fixed costs and $5 variable cost per tree.

1. BBREAKREAK VVENEN AANALYSNALYSIISSEE
AA PPRESENTATRESENTATIIONON BBYY,
RAVINDRA BABURAVINDRA BABU
PGDM – 1PGDM – 1STST
SEMSEM

2. INTRODUCTION..
 Break-even analysis is a useful tool to study the relationship
between fixed costs, variable costs and returns.
 Break even analysis gives the analysis of the Sales Volume
where the Variable Costs and Fixed Costs of the Products are
recovered.
 You can use break-even analysis to determine how much
product or service you need to sell at a specific price to meet
all costs.

3. INTRODUCTION.
 Break-even analysis is a mathematical
formula that discloses how much output
must be sold for the business to break
even.
 Break-even is reached when the money
coming in equals the money going out.

4. BREAK EVEN POINT
 It may be defined as the level of sales at which
the total revenue is equal to total costs and the
net income is zero.
 It is the point of activity where total revenue and
total expenses are equal.
 This is also known as “No Profit and No Loss”
zone.
 Breakeven Point = Fixed Costs/(Selling Price per
unit - Variable Cost per unit)

5. FIXED COST
Cost that do not change when production
or sales levels do change, such as rent,
property tax, insurance, or interest
expense. The fixed costs are summarized
for a specific time period (generally one
month).
VARIABLE COST
Variable costs are costs directly related
to production units. Typical variable
costs include direct labor and direct
materials. The variable cost times the
number of units sold will equal the Total
Variable Cost. Total Variable costs plus
Fixed costs make up the total cost of
production.

6. BREAK EVEN CHART
 In its simplest form, the break-even chart is a graphical
representation of costs at various levels of activity shown on the
same chart as the variation of income (or sales, revenue) with the
same variation in activity. The point at which neither profit nor
loss is made is known as the "break-even point" and is
represented on the chart below by the intersection of the two
lines
 In the diagram , the line OA represents the variation of income at
varying levels of production activity ("output"). OB represents the
total fixed costs in the business. As output increases, variable
costs are incurred, meaning that total costs (fixed + variable) also
increase. At low levels of output, Costs are greater than Income.
At the point of intersection, P, costs are exactly equal to income,
and hence neither profit nor loss is made.

7. BREAK EVEN CHART

8. COMPUTATION OF BREAK EVEN ANALYSIS
In the linear Cost-Volume-Profit Analysis model , the
break-even point (in terms of Unit Sales (X)) can be
directly computed in terms of Total Revenue (TR) and
Total Costs (TC) as:
where:
TFC is Total Fixed Costs,
P is Unit Sale Price, and
V is Unit Variable Cost

9. LINEAR BREAK-EVEN ANALYSIS
• Over small enough range of output levels,
TR and TC may be linear, assuming :
– Constant selling price (MR)
– Constant marginal cost (MC)
– Firm produces only one product
– No time lags between investment and resulting
revenue stream

10. LINEAR BEA EQUATION
ASSUME : TR=15Q, TFC=100, TVC=10Q.
THAT IS, IN TERMS OF TR AND TC FUNCTIONS,
TR = TC
HENCE,
TC=TFC+TVC
15Q = 100 + 10Q
5Q = 100
Q = 20
THUS, 20 IS THE BREAK-EVEN OUTPUT. GIVEN TR & TC FUNCTIONS,
PRODUCTION BEYOND 20 UNITS WILL YIELD INCREASING PROFITS,
(AT LEAST IN THE SHORT RUN).

11. TR
700
OP. PROFIT
TC
600
500
TVC
400
B
C& R
300
200 OP. LOSS
100 TFC
50
Q
10 20 30 40
output
LINEAR GRAPHLINEAR GRAPH

12. • The line TFC shows the total fixed cost and the line TVC shows the
variable cost.
• The line TC can be obtained also by a vertical summation of TFC and
TVC at various levels of o/p.
• The line TR shows the total revenue (TR) obtained with Q o/p.
• The line TR intersects the line TC at point b. the point b shows that at
Q, the firm’s total cost equals its total revenue. that is, at Q , TC breaks
even with tr. point b is, therefore, the break even point and Q is the
break-even level of o/p.
• Below Q level of o/p, TC >TR. the vertical difference between TC and
TR, (i.e., TC-TR) is known as operating loss.
• Beyond Q, TR>TC, and TR- TC is known as operating profit.
• It may thus be inferred that a firm producing a commodity under cost
and revenue conditions mentioned above must produce atleast Q
units to make its total cost and total revenue break even.

13. BREAK-EVEN ANALYSIS
Costs/Revenue
Output/Sales
FC
VC
TCTR TR
Q1
E

14.  Initially a firm will incur fixed costs, these do not depend on
output or sales.
 As o/p is generated, the firm will incur variable costs – these
vary directly with the amount produced
 The total costs therefore (assuming accurate forecasts!) is
the sum of FC+VC
 Total revenue is determined by the price charged and the
quantity sold – again this will be determined by expected
forecast sales initially.
 The lower the price, the less steep the total revenue curve.
 The Break-even point occurs where total revenue equals
total costs – the firm, in this example would have to sell Q1
to generate sufficient revenue to cover its costs.

15. BREAK-EVEN ANALYSIS
• Study of
interrelationships
among a firm’s sales,
costs, and operating
profit at various levels
of output
• Break-even point is
the Q where TR = TC
(Q1 to Q2 on graph)
TR
TC
Q
$’s
Profit
Q1 Q2

16. TC
B2
TOTAL TR
C & R
BI
F TFC
0
Q1 Q2
OUTPUT PER TIME UNIT
BEA - NON LINEAR GRAPH

17. • TFC line shows the fixed cost and the vertical distance between TC and
TFC measures the TVC.
• The curve TR shows the total sale proceeds or the total revenue (TR) at
different levels of o/p and price.
• The vertical distance between the TR and TC measures the profit or
loss for various levels of output .
• TR and TC curves intersect each other at two points, b1 and b2, where
TR = TC. these are the lower and upper break-even points.
• For the whole range of O/P b/w OQ1 (corresponding to break-even
point, b1) an OQ2 (corresponding to break-even point b2), TR>TC. It
implies that a firm produces more than OQ1 and less than OQ2 will
make profits. In other words, the profitable range of output lies
between OQ1 and OQ2 units of output. Producing less or more then
these limit will result in losses.

18. BEP AND PRICING..
• Importance of Price Elasticity of Demand:
• Higher prices might mean fewer sales to break-
even but those sales may take a longer time to
achieve.
• Lower prices might encourage more customers
but higher volume needed before sufficient
revenue generated to break-even

19. BEP AND PRICING..
Costs/Revenue
Output/Sales
FC
VC
TCTR (p = £2)
Q1
TR (p = £1)
Q3
If the firm chose to set prices lower (say £1) it would need to sell
more units before covering its costs

20. BEP AND PRICING.
Costs/Revenue
Output/Sales
FC
VC
TC
TR (p = Rs.2)
Q1
TR (p = Rs.3)
Q2
If the firm chose to set price higher than Rs.2 (say Rs.3) the TR curve would be
steeper – they would not have to sell as many units to break even.

21. BREAK-EVEN ANALYSIS.
Costs/Revenue
Output/Sales
FC
VC
TCTR (p = £2)
Q1
Loss
Profit

22. BREAK-EVEN ANALYSIS
Links of BE to pricing strategies and elasticity
• Penetration pricing – ‘high’ volume, ‘low’ price –
more sales to break even
• Market Skimming – ‘high’ price ‘low’ volumes –
fewer sales to break even
• Elasticity – what is likely to happen to sales when
prices are increased or decreased?

23. APPLICATION OF BEA..
•The break-even point is one of the simplest yet least
used analytical tools in management.
• It helps to provide a dynamic view of the
relationships between sales, costs and profits.
• A better understanding of break-even—for example,
expressing break-even sales as a percentage of actual
sales—can give managers a chance to understand
when to expect to break even (by linking the percent
to when in the week/month this percent of sales might
occur).
•The break-even point is a special case of Target
Income Sales, where Target Income is 0 (breaking
even).

24. ASSUMPTION.
 The cost and revenue function are linear.
 The total cost is divided into fixed and
variable costs.
 The selling price is constant.
 The volume of sales and volume of
production are identical.
 Average and marginal productivity of
factors are constant.
 Factor price is constant..

25. • IT IS STATIC AND UNREALISTIC
• Break-even analysis is only a supply side (i.e. costs only)
analysis, as it tells you nothing about what sales are actually
likely to be for the product at these various prices.
• It assumes that fixed costs (FC) are constant
•It assumes that the quantity of goods produced is equal to
the quantity of goods sold (i.e., there is no change in the
quantity of goods held in inventory at the beginning of the
period and the quantity of goods held in inventory at the
end of the period).
..

26. ALGEBRAIC SOLUTION.
• Equate total revenue and total cost functions and solve for Q
 TR = P x Q
 TC = FC + (VC x Q)
 TR = TC
 P x Q = FC + VC x Q
 Q(P-VC)=FC
 Q=FC/(P-VC)
 BREAK EVEN SALES=FC*SALES/(SALES-VC)

27. EXAMPLE 1 : How many Christmas trees
need to be sold ?
• Wholesale price per tree is $8.00
• Fixed cost is $30,000
• Variable cost per tree is $5.00
• Solution
Q(break-even) = FC/(P – VC) = $30,000/($8 - $5)
 = $30,000/$3 = 10,000 trees
 Break even sales are=10000*$8=$80,000

28. THANK YOU