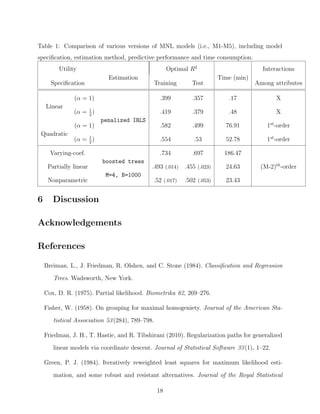
This document proposes applying boosting techniques to attraction-based demand models that are popular in pricing optimization. It formulates a multinomial likelihood for a semiparametric demand choice model (DCM) where product utility is specified without a fixed functional form. Gradient boosting is used to maximize the likelihood and estimate the nonparametric utility functions. The boosted tree-based approach flexibly models utility as a sum of trees, addressing limitations of existing DCMs like non-stationary demand and nonlinear attribute effects.

1. Boosted Multinomial Logit Model
September 10, 2012
Abstract
Understanding market demand is important to manage price strategies. Motivated by the
need to empirically estimate demand functions, we propose the application of boosting to
the class of attraction based demand model, which is popular in the pricing optimization
literature.In the proposed approach, the utility of a product is specified semiparametrically,
either by a varying-coefficient linear model or a partially linear model. We formulate the
multinomial likelihood and apply gradient boosting to maximize the likelihood. Several
attraction functions like the multinomial logit (MNL), linear and constant elasticity of sub-
stitution (CES) attraction functions are compared empirically and the implications of the
model estimates on pricing are discussed.
KEY WORDS: Boosting; functional gradient descent; tree-based regression; varying-
coefficient model.

2. 1 Introduction
Building a reliable demand model is critical for pricing and portfolio management. In build-
ing a demand model, we should consider customer preference about attributes, price sen-
sitivity, and competition effects. The model should have strong prediction power and still
being flexible.
In our model, we use aggregated mobile PC sales data from a third-party marketing firm.
The data includes HP & Compaq information, as well as competitors’ sales. Each row of the
data includes Brands, country, region, attributes, period, channel, price, and sales volume.
The sales data is large-scale, with thousands of rows and many columns, across different
time and region. Thus, we have a high-dimensional prediction problem, and need to allow
price sensitivity to vary with time, region and configuration.
Broadly speaking, there are two ways of building demand models: modeling sales volume
or customer preference. We focus on modeling customer valuation/preference using DCMs.
In DCM, we specify the choice set, the set of products the customers are choosing from.
Each product in the choice set has a utility, which depends on brand, attribute, price and
other factors. The customer chooses the product with the highest utility for purchase.
There are several complications with the utility function specification: nonlinearity and
non-additivity. Explain nonlinearity here. Further, the attribute effects are non-additive.
What we mean here is that, for example, the difference between the utility of 4GB RAM
and 2GB RAM may be different between different brands, or when combined with different
CPUs. Thus our model need to flexible. We achieve this by semiparametric DCM, to model
product utility without specifying a functional form. To flexibly model the utility functions,
we have proposed a novel boosted tree based varying-coefficient DCM. Assume that we have
a single market with M products. Briefly explain the formulation, and emphasize that in
the formulation, both intercept and slope are functions of a large number of mixed-type
variables, which makes the estimation problem really difficult. (The title of this page should
be varying-coefficient DCM given what you deleted.)
2

3. To estimate the nonparametric utility function written in the previous page, we use
boosted trees. The tree-base approach, use a heuristic algorithm, tries to partition the
products into homogeneous groups based on utility functions. We want the utility function
within a group to be as similar as possible, but between groups to be different. The right
hand side shows a demo of a simple tree with 4 nodes. We can see products are grouped based
on utility function, and the groups are formed by splitting on the features. The boosting
approach improves over the tree method, and it repeatedly generates trees to model the
“residuals” from the previous iteration. Thus the boosting result is a sum of trees, and on
the other hand, boosting is a way of maximizing likelihood that contains unknown functions.
Other use cases of the model include feature importance plot and brand level utility
functions. The feature importance plot tell us which features are importance in determining
utility function, and brand level utility functions give us ideas of brand value and price
sensitivity within each brand.
The remainder of the paper proceeds as follows.
2 Literature Review
We discuss two streams of literature that are relevant to this research: multinomial logit
demand modeling, and boosting.
Most demand research is constructed upon a structure of how demand responses to
prices. This paper is no exception. The multinomial logit (MNL) discrete choice model
is particularly popular after it was first proposed by McFadden (?) because of appealing
theoretical properties (consistency with random utility choices) and ease of application to
empirical studies. It has received significant attention by researchers from economics, mar-
keting, transportation science and operations management, and it has motivated tremendous
theoretical research and empirical validations in a large range of applications. The MNL is
a special case of the class of attraction models proposed by Luce (?). See also Ben-Akiva,
and Lerman (?) for a thorough review of choice models.
3

4. In most literature (for example, Berry 1994 and Kamkura, Kim and Lee 1996), the utility
function is assumed to be stationary and linear in product attributes. In practice, these
assumptions are seldom true. (cite tree based paper) addresses both issues. Time varying
coefficients are used to incorporate non-stationary demand. In addition, (tree base paper)
uses a non-parametric approach to specific the structure of the utility function. In particular,
a modified tree-base regression method is used to discover the nonlinear dependencies on,
and interaction effects between product attributes, in a MNL framework.
(add boosting literature here)
The main contribution of this paper is to apply boosting method to tree-based and time
varying coefficient MNL demand models. From a modeling perspective, the tree-based and
time varying coefficient MNL models successfully addresses two of the major criticisms of
MNL models. However, both models are challenging to estimate empirically because the
search space for potential specifications is large with little known structure to be exploited.
For example, the standard binary splitting method to estimate the tree-based MNL model
is path dependent, and potentially results in sub-optimal estimation. Boosting alleviates
some of these problems. In empirical test of field data, boosting can improve out-of-sample
performance by x%.
3 Boosted Multinomial Logit Model
In this exposition, consider a single market with K products in competition. The market
could be a mobile computer market in a geographical location over a period of time, or an
online market for certain non-perishable goods. The notion of a product could potentially
include “non-purchase” option. Denote the sales volume of the i-th product as ni, where
i = 1, · · · , K. The total market size is denoted as N = K
i=1 ni. Further, let (si, xi, ni)
denote the vector of measurements on product i. Here, si = (si1, si2, · · · , siq) consists of
product attributes, brand and channel information, whose effect on utility has an unknown
functional form. The vector of linear predictors is xi = (xi1, xi2, · · · , xip) , often consisting
4

5. of price or other predictors with linear effects.
The utility of a product captures the overall attractiveness given attributes, brand, price
and factors relating to customers’ shopping experience. The utility is often positively cor-
related with product attributes, but is adversely affected by price. The utility of the i-th
product is denoted as
ui = fi + i,
where fi is a deterministic function of si and xi, and i denotes the random noise term
not captured by the auxiliary variables, arising from the idiosyncratic errors in customers’
decision making. If we assume that the i’s are independent and identially distributed with
standard Gumbel distribution, then a utility maximization principle leads to the following
expression of the choice probability for the i-th product,
pi =
exp(fi)
K
i=1 exp(fi)
. (1)
Further, we assume the vector of sales volume (n1, · · · , nM ) follows multinomial distribution
with N trials and probabilities (p1, · · · , pK) defined by (1). The resulting model is called
the multinomial logit (MNL) model. The attraction function in MNL model is exponential,
which can be generalized to arbitrary attraction functions. Let g(·) denote the attraction
function generically, which is a known monotone function that takes values on (0, +∞).
Under attraction function g(·), the choice probability of product i is,
pi =
g(fi)
K
i=1 g(fi)
. (2)
To estimate the utility functions, we can maximize the data likelihood, or equivalently,
minimize the −2 logL where L denotes the multinomial likelihood function. Without causing
much confusion, we will work with J(f) defined below, which differs from −2 logL by a
constant,
J(f) = −2
K
i=1
ni {log(g(fi))} + 2Nlog
K
i=1
g(fi) , (3)
where f = (f1, · · · , fK) denotes the vector of product utilities. The model can also be
regarded as poisson regression model conditioning on the total sales volume in a consideration
5

6. set, also known as conditional poisson regression. The model is conceptually similar to the
stratified Cox’s proportional hazard model with an offset term that depends on the surviving
cases in the corresponding stratum (Cox 1975, Hosmer and Lemeshow 1999).
We consider two semiparametric models of utility: the functional-coefficient model and
partially linear model, and refer to the resulting choice models as functional-coefficient and
partially linear choice models, respectively.
Functional-coefficient MNL
In functional-coefficient MNL model, we specify the utility function as
fi = xiβ(si), (4)
which is a linear function of x with coefficients depending on s. The function reduces to
a globally linear function once we remove the dependence of the coefficients on s, which
corresponds to a linear MNL model. In simple cases with xi = (1, xi) where xi is the price
of product i, the utility function becomes β0(si) + β1(si)xi. Here, both the base utility and
price elasticity depend on si, and the price coefficient is constant when si is fixed.
Our estimation of the coefficient surface β(si) involves minimizing the following −2log-
likelihood by boosted varying-coefficient trees:
J(f) = −2
K
i=1
ni {log(g(xiβ(si)))} + 2Nlog
K
i=1
g(xiβ(si)) .
The technical details for growing varying-coefficient trees can be found in Wang and Hastie
(2012), and are briefly reviewed in section 4.1 of the current paper. As shown in Algorithm 1,
our proposed method starts with an estimate of the constant-coefficient linear MNL model,
iteratively constructs varying-coefficient trees, and then fits linear MNL models using tree-
generated bases. The incremental trees are grown in such a way that best predict the pseudo
observations ξi, which represent the gradient for minimizing J(f).
The estimation of the linear MNL model involves iteratively reweighted least squares,
or IRLS (Green 1984). We take the initial estimates as an example. Let β
(b−1)
denote the
6

7. estimate from the (b − 1)-th iteration, and ˆp
(b−1)
i denote the fitted choice probability. Next,
we construct pseudo response as
˜y
(b)
i = xiβ
(b−1)
+
ni
N
− ˆp
(b−1)
i
ˆp
(b−1)
i (1 − ˆp
(b−1)
i )
,
and fit ˜y
(b)
i on xi using weighted least squares with observation weight ˆp
(b−1)
i (1− ˆp
(b−1)
i ). This
procedure is iterated until convergence.
Algorithm 1 Boosted Functional-coefficient MNL.
Require: B – the number of boosting steps, ν – the “learning rate”, and M – number of
terminal nodes for a single tree.
1. Start with naive fit ˆf
(0)
i = xi
ˆβ, where ˆβ is estimated via iteratively reweighted least
squares (IRLS) under a linear MNL model.
2. For b = 1, · · · , B, repeat:
(a) Compute the “pseudo observations”: ξi = − ∂φ
∂fi f= ˆf(b−1)
.
(b) Fit ξi on si and xi using the “PartReg” algorithm to obtain partitions
(C
(b)
1 , · · · , C
(b)
M ).
(c) Let zi = (I(si∈C
(b)
1 )
, · · · , I(si∈C
(b)
M )
, xiI(si∈C
(b)
1 )
, · · · , xiI(si∈C
(b)
M )
) , and apply IRLS
to estimate γ(b)
by minimizing
J(γ(b)
) = −2
K
i=1
ni log(g( ˆf
(b−1)
i + ziγ(b)
)) + 2Nlog
K
i=1
g( ˆf
(b−1)
i + ziγ(b)
) ,
and denote the estimated vector as γ(b)
= (γ
(b)
01 , · · · , γ
(b)
0M , γ
(b)
11 , · · · , γ
(b)
1M ) .
(d) Update the fitted model by ˆf(b)
= ˆf(b−1)
+ ν M
m=1 γ
(b)
0m + γ
(b)
1mxi I(si∈C
(b)
m )
.
3. Output the fitted model ˆf = ˆf
(B)
.
7

8. Partially Linear MNL
In partially linear choice model, we specify the utility function as
fi = β0(si) + xiβ, (5)
which consists of a nonparametric term β0(si) and a linear term xiβ. If the linear predictors
include the price only, the resulting model consists of a base utility that is a nonparametric
function of attributes, and a globally constant price elasticity. In a refined model, interactions
between price and other factors like brand or product category can be incorporated into the
design matrix of the linear term xiβ, to allow the price coefficient to vary along certain
dimensions. Another interesting special case of partially linear MNL is a nonparametric
MNL model, by removing the linear predictors xi and only fitting a nonparametric utility
function. All the special cases can be estimated under the same boosted tree framework.
The boosting algorithm for the partially linear model is explained in Algorithm 2. Here,
the varying intercept β0(si) is initially fitted with a constant value, and then approximated
by piecewise constant trees using the CART algorithm. At every stage, the search for
optimal partitioning in CART and the estimation of β are conducted sequentially, instead
of simultaneously. Specifically, we search for the optimal tree split for predicting the pseudo
residuals, ignoring the linear predictors, and then fit a linear MNL model using the tree
grouping and the original predictors xi jointly.
4 Computational Details
4.1 Tree-based Varying-coefficient Regression
The estimation of the boosted varying-coefficient MNL model involves iteratively applying
the “PartReg” algorithm for constructing tree-based regressions. Let (si, xi, yi) denote the
measurements on subject i, where i = 1, · · · , n. Here, the varying-coefficient variable or par-
tition variable, is si = (si1, si2, · · · , siq) and the regression variable is xi = (xi1, xi2, · · · , xip) .
8

9. Algorithm 2 Boosted Partially Linear MNL model.
Require: B – the number of boosting steps, ν – the “learning rate”, and M – the number
of terminal nodes for a single tree.
1. Start with naive fit ˆf
(0)
i = ˆβ0 + xi
ˆβ, where ˆβ0 and ˆβ are estimated via Newton-
Raphson algorithm or IRLS.
2. For b = 1, · · · , B, repeat:
(a) Compute the “pseudo observations”: ξi = − ∂J
∂fi f=ˆf
(b−1)
.
(b) Fit ξi on si using the CART algorithm (Breiman et al. 1984) to obtain
ξi =
M
m=1
˜ξ(b)
m I(si∈C
(b)
m )
.
(c) Let zi = (I(si∈C
(b)
1 )
, · · · , I(si∈C
(b)
M )
) , and apply IRLS to minimize
J(γ0, γ) = −2
K
i=1
ni log(g( ˆf
(b−1)
i + ziγ0 + xiγ)) +2Nlog
K
i=1
g( ˆf
(b−1)
i + ziγ0 + xiγ) ,
and denote the estimates as (ˆγ
(b)
0m, · · · , ˆγ
(b)
0m, ˆγ(b)
).
(d) Update the fitted regression function by ˆf
(b)
i = ˆf
(b−1)
i +
ν M
m=1 ˆγ
(b)
0mI(si∈C
(b)
m )
+ νxiγ(b)
.
3. Output the fitted model ˆf = ˆf
(B)
.
9

10. The two sets of variables are allowed to have overlaps. The first element of xi is set to be 1
if we allow for an intercept term.
Let {Cm}M
m=1 denote a partition of the space Rq
satisfying Cm ∩Cm = ∅ for any m = m ,
and ∪M
m=1Cm = Rq
. The set Cm is referred to as a terminal node or leaf node, which defines
the ultimate grouping of the observations. Here, M denotes the number of partitions. The
number of tree nodes M is fixed when the trees are used as base learners in boosting. The
tree-based varying-coefficient model is
yi =
M
m=1
xiβmI(si∈Cm) + i, (6)
where I(·) denotes the indicator function with I(c) = 1 if event c is true and zero otherwise.
The error terms is are assumed to have zero mean and homogeneous variance σ2
.
The least squares criterion for (6) leads to the following estimator of (Cm, βm), as mini-
mizers of sum of squared errors (SSE),
(Cm, ˆβm) = arg min
(Cm,βm)
n
i=1
yi −
M
m=1
xiβmI(si∈Cm)
2
= arg min
(Cm,βm)
n
i=1
M
m=1
(yi − xiβm)
2
I(si∈Cm).
(7)
In the above, the estimation of βm is nested in that of the partitions. We take the least
squares estimator,
ˆβm(Cm) = arg min
βm
n
i=1
(yi − xiβm)
2
I(si∈Cm),
in which the minimization criterion is essentially based on the observations in node Cm only.
Thus, we can “profile” out the regression parameters βm and have
Cm = arg min
Cm
M
m=1
SSE(Cm) := arg min
Cm
n
i=1
M
m=1
yi − xi
ˆβm(Cm)
2
I(si∈Cm), (8)
where SSE(Cm) := arg minCm
n
i=1 (yi − xiβm)2
I(si∈Cm).
The sets {Cm}M
m=1 comprise an optimal partition of the space expanded by the partition-
ing variables s, where the “optimality” is with respect to the least squares criterion. The
search for the optimal partition is of combinatorial complexity, and it is of great challenge
to find the globally optimal partition even for a moderate-sized dataset. The tree-based
10

11. algorithm is an approximate solution to the optimal partitioning and scalable to large-scale
datasets. We restrict our discussions to binary trees that employ “horizontal” or “vertical”
partitions of the feature space and are stage-wise optimal.
In Algorithm 3, we cycle through the partition variables at each iteration and consider
all possible binary splits based on each variable. The candidate split depends on the type
of the variable. For an ordinal or a continuous variable, we sort the distinct values of the
variable, and place “cuts” between any two adjacent values to form partitions.
Splitting based on an unordered categorical variable is challenging, especially when there
are many categories. We propose to order the categories and treat the variable as an ordinal
variable. The ordering approach is much faster than exhaustive search, and performs com-
parably to the more complex search algorithms when combined with boosting. The category
ordering approach is similar to CART (Breiman et al. 1984). In a piecewise constant model
like CART, the categories are ordered based on the mean response in each category, and
then treated as ordinal variables (Hastie et al. 2009). This reduces the computation com-
plexity from exponential to linear. The simplification was justified by Fisher (1958) in an
optimal splitting setup, and is exact for a continuous-response regression problem where the
mean is the modeling target. In the partitioned regression context, let ˆβl denote the least
squares estimate of β based on observations in the l-th category. The fitted model in the
l-th category is denoted as x ˆβl. A strict ordering of the hyperplanes x ˆβl may not exist,
thus we suggest an approximate solution. We propose to order the L categories using ¯x ˆβl,
where ¯x is the mean vector of xis in the current node, and then treat the categorical variable
as ordinal. This approximation works well when the fitted models are clearly separated, but
is not guaranteed to provide an optimal split at the current stage.
4.2 Split Selection
The partitioning algrithms CART and “PartReg” aim at achieving optimal reduction of
complexity at each stage. In exhaustive search, the number of binary partitions for an ordinal
11

12. Algorithm 3 “PartReg” Algorithm (Breadth-first search).
Require: n0– the minimum number of observations in a terminal node and M– the desired
number of terminal nodes.
1. Initialize the current number of terminal nodes l = 1 and Cm = Rq
.
2. While l < M, loop:
(a) For m = 1 to l and j = 1 to q, repeat:
i. Consider all partitions of Cm into Cm,L and Cm,R based on the j-th
variable. The maximum reduction in SSE is,
∆SSEm,j = max{SSE(Cm) − SSE(Cm,L) − SSE(Cm,R)}, (9)
where the maximum is taken over all possible partitions based on the
j-th variable such that min{#Cm,L, #Cm,R} ≥ n0 and #C denotes the
cardinality of set C.
ii. Let ∆SSEl = maxm maxj ∆SSEm,j, namely the maximum reduction in
the sum of squared error among all candidate splits in all terminal nodes
at the current stage.
(b) Let ∆SSEm∗,j∗ = ∆SSEl, namely the j∗
-th variable on the m∗
-th terminal node
provides the optimal partition. Split the m∗
-th terminal node according to the
optimal partitioning criterion and increase l by 1.
12

13. variable with L categories is L − 1 and the number is 2L−1
− 1 for a categorical variable.
Thus, the number of possible partitions for a categorical variable grows exponentially, which
has greatly increased the search space, causing the tree splitting to favor the categorical
variables. Our varying-coefficient tree algorithm takes a response-driven ordering of the
categories, and has alleviated the issue with unfair split selection to some extent. But bias
remains with the current method, resulting from the following aspects:
1. The response-driven ordering of the nominal categories can cause bias to split selection.
2. The number of categories is unequal among various variables.
Thus, the direct use of the tree or boosting algorithm for inference, especially on variable
importance, should be cautioned. To further reduce the bias in split selection, we adopt a
pretest procedure using the analysis of covariance (ANCOVA). The use of significance testing-
based procedure in decision trees dates back to the CHAID technique (Kass 1980), in which
a Bonferroni factor was introduced in classification based on multi-way splits. A number of
algorithms explicitly dealt with split selection in classification or regression tree, including the
FACT (Loh and Vanichsetakul 1988), GUIDE (Loh and Shih 1997), and QUEST algorithms
(Loh 1997), among others. Hothorn et al. (2006) proposes to use permutation test to select
the split variable and a multiple testing procedure for testing the global null hypothesis that
none of the predictors is significant. In the context of boosting, the recent Hofner et al.
(2011) paper proposes to use component-wise learners with comparable degrees of freedom,
and the degrees of freedom are made comparable by ridge penalty. The simulation has shown
satisfactory results under the null model, in which the response variable is independent of
the covariates.
5 Mobile Computer Sales in Australia
The proposed semiparametric MNL models have been applied to the aggregated monthly
mobile computer sales data in Australia, obtained from a third-party marketing firm. The
13

14. dataset contains the sales volume of various categories of mobile computers, including lap-
tops, netbooks, hybrid tablets, ultra-mobile personal computers and so on. The monthly
sales data goes from October 2010 to March 2011, and covers all mobile computer brands
on the Austalian market. Every row of the data set contains detailed configurations of the
product, the sales volume, the revenue generated from selling the product in certain month
and state. The average selling price is derived by taking the ratio of the revenue to the sales
volume.
The data contains 6 months of mobile computer sales in 5 Australian states. A choice
set is defined as the combination of a month and a state, leading to 30 choice sets. A choice
set contains approximately 100 to 200 products under competition. Other definitions of a
choice set have also been attempted, but for the sake of brevity, we only present results under
this definiton of a choice set. We randomly select 25 choice sets as the training data and
the remaining 5 as test data. In this paper, we only present the model estimates with price
residuals (denoted as xi without causing much confusion) as the linear predictor, instead of
the original price. The price residuals are the linear regression residuals after we fit price on
product attributes and brand. The residuals are now uncorrelated with product attributes,
and a demand model using the residuals as input usually leads to higher price sensitivities.
Without causing much confusion, we denote the residual of the i-th observation as xi.
We have considered five specifications of the mean utility function, including two es-
sentially linear specifications and three nonparametric or semiparametric models. The two
intrinsically linear choice models are estimated using elastic net (Zou and Hastie 2005) which
will be explained in detail in the next section, and the remaining models are estimated via
boosted trees. The five models are listed below:
M1. Varying coefficient-MNL model:
fi = xiβ(si) = β0(si) + β1(si)xi. (10)
Here, the utility is a linear function of price residuals with coefficients depending on
14

15. attributes, brand and sales channel. The multivariate coefficient surface β(si) is of
estimation interest.
M2. Partially linear-MNL model:
fi = β0(si) + xiβ1.
The utility consists of a base utility, which is a nonparametric function of product
attributes and reportting channel, and a linear effect of price residuals. This model
assumes constant price effect on the utility.
M3. Nonparametric-MNL model:
fi = β(si, xi).
Here, the utility is a nonparametric function of the entire set of predictors. Customers’
sensitivity to price is implicit, rather than explicitly specified.
M4. Linear-MNL model. The coefficient β(si) in (10) is approximated by a linear function
of si, and the model is estimated using penalized iteratively reweighted least squares
(IRLS).
M5. Quadratic-MNL model. We approximate the coefficient β(si) in (10) by a quadratic
function of si with first-order interactions among the elements of si. The model is
again estimated using penalized IRLS.
Elastic net varying-coefficient MNL
We take the quadratic MNL as an example for explaining the penalized IRLS algorithm in
MNL models. The first step is to generate the feature vector, in which we first create dummy
variables based on categorical variables, and then generate design matrix Z by including both
the quadratic effect of individual variables and first-order interaction effect between pairs of
variables. We denote the i-th row of Z as zi, and then specify β0(si) as ziγ0 and β1(si) as
15

16. ziγ1. Next, we seek to estimate the following penalized generalized linear model:
(γ0, γ1) = arg minγ0,γ1
−2
K
i=1
nilog(g(ziγ0 + (zixi)γ1)) + 2Nlog
K
i=1
g(ziγ0 + (zixi)γ1)
+ λ α
i,j
|γij| +
(1 − α)
2 i,j
γ2
ij . (11)
In the penalized regression above, the penalty is a convex combination of L1 and L2 penalty
with tuning parameter α controling the relatively weight of the respective penalty. Model
(11) reduces to ridge regression if we set α as 0 and reduces to LASSO regression if α = 1.
The penalized linear MNL model (11) can be estimated by penalized IRLS algorithm
(Friedman et al. 2010). Let γ
(b−1)
0 and γ
(b−1)
1 denotes estimates from the (b−1)-th iteration,
and ˆp
(b−1)
i denotes the fitted probabilities. In the next iteration, we construct pseudo response
as
˜y
(b)
i = ziγ
(b−1)
0 + zixiγ
(b−1)
1 +
ni
N
− ˆp
(b−1)
i
ˆp
(b−1)
i (1 − ˆp
(b−1)
i )
,
and fit ˜y
(b)
i on (zi, zixi) with weights ˆp
(b−1)
i (1 − ˆp
(b−1)
i ) and the elastic net penalty. The
elastic net penalized weighted least squares can be implemented by the glmnet package in
R, and iterated until convergence.
The three nonparametric or semiparametric models are estimated via boosted trees. The
varying-coefficient MNL model is estimated with Algorithm 1 and the remaining two models
are estimated with Algorithm 2 or its variant. The base learner is an M-node tree with
M = 4, and the learning rate is specified as ν = 0.1. In Figure 1, we plot training and test
sample R2
s against tuning parameter for models M1-M3 and M5 (α = 1). For the three
models estimated with boosted trees, the R2
increases dramatically before 200 iterations,
but the improvement slows down when the number of iterations further increases. We do
not observe significant overfitting when the number of boosting iterations gets much larger.
The five MNL models are compared in Table 1 in terms of model implications, predictive
performance and time spent. The varying-coefficient MNL model has the best predictive
16

17. 0 200 400 600 800 1000
0.00.20.40.60.81.0
Varying coefficient−MNL, Boosted
Iterations
R2
Training
Test
0 200 400 600 800 1000
0.00.20.40.60.81.0
Partially linear, Boosted
Iterations
R2
Training
Test
0 200 400 600 800 1000
0.00.20.40.60.81.0
Nonparametric, Boosted
Iterations
R2
Training
Test
−5 −4 −3 −2 −1
0.00.20.40.60.81.0
glmnet, alpha=1
log(lambda)
R2
Training
Test
Figure 1: The training and test sample R2
, plotted against tuning parameters, under the
varying-coefficient MNL (top left), partially linear MNL (top right), nonparametric MNL
(bottom left) and quadratic MNL model with LASSO penalty (bottom right).
performance among all five models, followed by penalized quadratic MNL models. The
nonparametric MNL model has inferior performance to the other two semiparametric models,
which is contradictory to the fact that this model includes the other two as special cases.
One possible explanation is that the tree-based method fails to learn variable interactions,
especially the interaction between xi and si. Unfortunately, the varying-coefficient MNL
takes the longest to fit, if no significance test is performed. The pretest-based approach
speeds up the boosting algorithm, but slightly deteriorates the model performance. Both
partially linear and nonparametric MNLs are much faster than varying-coefficient MNL,
given the use of the built-in rpart function instead of user-defined tree growing algorithm.
17

18. Table 1: Comparison of various versions of MNL models (i.e., M1-M5), including model
specification, estimation method, predictive performance and time consumption.
Utility Optimal R2
Interactions
Specification
Estimation
Training Test
Time (min)
Among attributes
(α = 1) .399 .357 .17 X
Linear
(α = 1
2
) .419 .379 .48 X
(α = 1)
penalized IRLS
.582 .499 76.91 1st
-order
Quadratic
(α = 1
2
) .554 .53 52.78 1st
-order
Varying-coef. .734 .697 186.47
Partially linear
boosted trees
.493 (.014) .455 (.023) 24.63 (M-2)th
-order
Nonparametric
M=4, B=1000
.52 (.017) .502 (.053) 23.43
6 Discussion
Acknowledgements
References
Breiman, L., J. Friedman, R. Olshen, and C. Stone (1984). Classification and Regression
Trees. Wadsworth, New York.
Cox, D. R. (1975). Partial likelihood. Biometrika 62, 269–276.
Fisher, W. (1958). On grouping for maximal homogeniety. Journal of the American Sta-
tistical Association 53(284), 789–798.
Friedman, J. H., T. Hastie, and R. Tibshirani (2010). Regularization paths for generalized
linear models via coordinate descent. Journal of Statistical Software 33(1), 1–22.
Green, P. J. (1984). Iteratively reweighted least squares for maximum likelihood esti-
mation, and some robust and resistant alternatives. Journal of the Royal Statistical
18

19. Society, Series B 46(2), 149–192.
Hastie, T., R. Tibshirani, and J. Friedman (2009). The Elements of Statistical Learning:
Data Mining, Inference, and Prediction. Springer-Verlag, New York.
Hofner, B., T. Hothorn, T. Kneib, and M. Schmid (2011). A framework for unbiased model
selection based on boosting. Journal of Computational and Graphical Statistics 20(4),
956–971.
Hosmer, D. W. J. and S. Lemeshow (1999). Applied survival analysis: regression modeling
of time to event data. John Wiley & Sons.
Hothorn, T., K. Hornik, and A. Zeileis (2006). Unbiased recursive partitioning: A condi-
tional inference framework. Journal of Computational and Graphical Statistics 15(3),
651–674.
Kass, G. V. (1980). An exploratory technique for investigating large quantities of categor-
ical data. Applied Statistics 29, 119–127.
Loh, W.-Y. (1997). Regression trees with unbiased variable selection and interaction de-
tection. Statistica Sinica 12, 361–386.
Loh, W.-Y. and Y.-S. Shih (1997). Split selection methods for classification trees. Statistica
Sinica 7, 815–840.
Loh, W.-Y. and N. Vanichsetakul (1988). Tree-structured classification via generalized
discriminant analysis (with discussion). Journal of the American Statistical Associa-
tion 83, 715–728.
Wang, J. C. and T. Hastie (2012). Boosted varying-coefficient regression models for prod-
uct demand prediction. Under revision.
Zou, H. and T. Hastie (2005). Regularization and variable selection via the elastic net.
Journal of the Royal Statistical Society, Series B 67(2), 301–320.
19