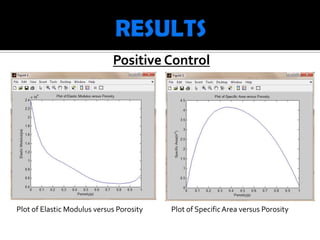
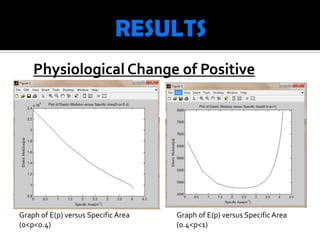
This document describes modeling the relationship between porosity and elastic modulus of bone. Equations 1-3 model elastic modulus as a function of porosity using Matlab and Excel. Plots show the relationship between elastic modulus and porosity, and specific surface area and porosity. The original model determines optimal porosity for maximum elastic modulus. The new model provides a more accurate way to analyze bone fractures and predict recovery by demonstrating how specific surface area affects elastic modulus. Results unexpectedly showed elastic modulus increasing with surface area above 2.6m-1 for porosity over 0.4.

1. Chun Hoe Ong
11/12/2012
BIEN 430

2.  Mechanical damage fatigue dynamics
coupled with bone cell activities in creating
bone remodeling models.
What is being modeled?
 The modulus of elasticity as a function of
porosity
What is being changed?
 Porosity Function

3.  Matlab
 Matlab: used as the primary means of recreating
the positive control model.
 Microsoft Excel
 Excel: used to validate Matlab’s plots and to
recreate equations.

4.  Equation 1
Where E = Young’s modulus
p= Porosity
 Equation 2
Where s= Specific Area
p= Porosity

5.  Equation 3
Where E= Absolute Young’s Modulus
p= Porosity

6. Positive Control
Plot of Elastic Modulus versus Porosity Plot of Specific Area versus Porosity

7. Physiological Change of Positive
Control
Graph of E(p) versus Specific Area Graph of E(p) versus Specific Area
(0<p<0.4) (0.4<p<1)

8.  Bone is dynamic tissue that adepts its
microstructure to its physiological and
mechanical environment. (Consistent with
Wolff’s Law)

9.  The original model allows us to determine the
optimal porosity to obtain the maximum
elastic modulus.
 Can be used to study long-term effects of
mechanical damage on bone recovery.
 Provides a method of predicting when a bone
might fracture.

10.  Can be used in combination of finite element
code to asses strategies for knee
replacement.
Significance of New Model
 Provides a more accurate method of
analyzing bone fractures
 Demonstrates the effects of change in
specific area on the elastic modulus of bone.
 Allows for a better prediction of bone
recovery rate

11. Unexpected Results
 The modulus of elasticity began to increase
as the surface area increased beyond 2.6m-1
for porosity> 0.4
 The exponential increase of the Young’s
modulus once the surface area increased
beyond 2.6m-1 for porosity> 0.4