Tài liệu nghiên cứu về việc sử dụng MATLAB trong lĩnh vực kỹ thuật, bao gồm các khái niệm cơ bản về MATLAB, các hàm toán học và cách thao tác với ma trận. Nó cũng giới thiệu cách giải một số bài toán kỹ thuật thông qua ứng dụng MATLAB và nhấn mạnh tính hiệu quả của phần mềm trong việc giải quyết các vấn đề toán học phức tạp. MATLAB được mô tả là một công cụ mạnh mẽ giúp sinh viên và nhà nghiên cứu nâng cao năng lực tính toán và tiết kiệm thời gian lập trình.

1. THUYẾT MINH ĐÈ TÀI
NGHIÊN CỨU KHOA HỌC CẤP
TRƯỜNG: MATLAB TÌM HIỂU
VÀ ỨNG DỤNG

2. Tr−êng ®¹I häc giao th«ng vËn t¶I
thuyÕt minh
®Ò tµI nghiªn cøu khoa häc cÊp tr−êng
matlab
t×m hiÓu vµ øng dông
gi¶i mét sè bµi to¸n kÜ thuËt
M· sè : T2001- CK- 08
Ng−êi thùc hiÖn : Th.S NguyÔn B¸ NghÞ
K.S NguyÔn v¨n Chung
K.S Ph¹m thÕ Minh
§¬n vÞ : Bé m«n KÜ thuËt m¸y
Khoa C¬ khÝ
HANOI - 2002

3. môc lôc
PhÇn 1 Giíi thiÖu vÒ Matlab
1. B¾t ®Çu víi Matlab
2. C¸c kh¸i niÖm c¬ b¶n
a. C©u lÖnh vµ biÕn
b. C¸c phÐp to¸n
c. Sè dïng trong Matlab
d. NhËp sè liÖu tõ bµn phÝm
e. In kÕt qu¶ ra mµn h×nh
f. Ma trËn
g. Sè phøc vµ ma trËn phøc
3. C¸c hµm to¸n häc
a. C¸c hµm l−îng gi¸c
b. C¸c hµm to¸n s¬ cÊp
4. C¸c thao t¸c ®Æc biÖt trªn ma trËn
5. Thùc hiÖn c¸c phÐp tÝnh trªn ma trËn
a. C¸c phÐp tÝnh trªn ma trËn
b. C¸c phÐp tÝnh phÇn tö - phÇn tö cña ma trËn
6. C¸c hµm thùc hiÖn c¸c phÐp tÝnh vÒ ®a thøc
7. C¸c hµm ph©n tÝch d÷ liÖu
8. Hµm cña hµm
a. Hµm tÝch ph©n sè
b. Hµm t×m nghiÖm ph−¬ng tr×nh phi tuyÕn vµ c¸c hµm tèi −u
c. Hµm gi¶i ph−¬ng tr×nh vi ph©n
9. C¸c to¸n tö ®iÒu khiÓn
10. C¸c lo¹i file trong Matlab
11. Xö lÝ tÝn hiÖu
12. VÏ ®å thÞ

4. PhÇn 2 øng dông Matlab gi¶i mét sè
bµi to¸n kÜ thuËt
1. Bµi to¸n vÒ m¹ch ®iÖn
2. Gi¶i bµi to¸n ®éng häc c¬ cÊu ph¼ng
3. Gi¶i bµi to¸n c©n b»ng m¸y
4. TÝnh thiÕt kÕ bé truyÒn b¸nh r¨ng
5. TÝnh søc bÒn trôc
6. TÝnh dao ®éng
a. TÝnh dao ®éng hÖ mét bËc tù do
b. TÝnh dao ®éng hÖ hai bËc tù do
c. X¸c ®Þnh tÇn sè dao ®éng riªng cña hÖ nhiÒu bËc tù do
KÕt luËn
tµi liÖu tham kh¶o

5. Giíi thiÖu
MATLAB lµ mét bé phÇn mÒm dïng ®Ó tÝnh to¸n c¸c bµi to¸n kÜ thuËt,
®−îc viÕt b»ng ng«n ng÷ C do h·ng Math Works Inc. s¶n xuÊt. Nã ®−îc
t¹o trªn c¬ së nh÷ng phÇn mÒm do c¸c nhµ lËp tr×nh cña c¸c dù ¸n
LINPACK vµ EISPACK viÕt ra b»ng ng«n ng÷ Fortran dïng cho viÖc
thùc hiÖn c¸c phÐp tÝnh vµ thao t¸c trªn ma trËn.
Tªn cña phÇn mÒm MATLAB lµ ch÷ viÕt t¾t cña ‘ matrix laboratory’ cã
nghÜa lµ ‘ph−¬ng ph¸p ma trËn’. §Õn khi thùc hµnh sö dông phÇn mÒm ta
sÏ thÊy mçi phÇn tö c¬ b¶n cña MATLAB lµ mét ma trËn.
MATLAB liªn tôc ®−îc bæ sung vµ hoµn thiÖn. Thêi gian gÇn ®©y h·ng
s¶n xuÊt ®· cho ra phiªn b¶n míi nhÊt lµ MATLAB 6.0.
Matlab lµ mét phÇn mÒm rÊt m¹nh, cho phÐp gi¶i rÊt nhanh c¸c bµi to¸n
ph©n tÝch sè liÖu, tÝnh to¸n ma trËn, xö lÝ tÝn hiÖu, m« pháng vµ t¹o vÏ ®å
thÞ ... LÝ do v× Matlab ®· cã mét lo¹t c¸c hµm chuyªn gi¶i quyÕt c¸c vÊn
®Ò ®ã ®−îc ®Æt trong Toolbox. Thªm n÷a, Matlab l¹i rÊt dÔ sö dông: nã
kh«ng cÇn khai b¸o biÕn, c¸c c©u lÖnh ®−îc viÕt rÊt gÇn gòi nh− khi viÕt
c¸c biÓu thøc to¸n häc, tiÕt kiÖm rÊt nhiÒu thêi gian cho viÖc lËp tr×nh.
Mét ®Æc ®iÓm næi bËt n÷a cña Matlab lµ nã cã kh¶ n¨ng më réng: ng−êi
sö dông cã thÓ tù s¸ng t¹o nh÷ng file hµm ®Æt vµo Toolbox ®Ó thùc hiÖn
gi¶i nh÷ng ba× to¸n trong lÜnh vùc chuyªn m«n cña m×nh.
Sau mét thêi gian tù t×m hiÓu vµ øng dông chóng t«i thÊy r»ng MATLAB
lµ mét phÇn mÒm rÊt thÝch hîp cho viÖc gi¶i c¸c bµi to¸n kÜ thuËt trong
nhiÒu lÜnh vùc. §Æc biÖt trong c¸c tr−êng §¹i häc kÜ thuËt nã cã thÓ gióp
cho c¸c c¸n bé nghiªn cøu vµ sinh viªn cã ®−îc mét c«ng cô s¾c bÐn ®Ó
n©ng cao n¨ng lùc tÝnh to¸n, tiÕt kiÖm thêi gian lËp tr×nh.
§ã lµ lÝ do ®Ó nhãm nghiªn cøu chóng t«i m¹nh d¹n thùc hiÖn ®Ò tµi cã
tÝnh chÊt t×m hiÓu, giíi thiÖu vµ thö øng dông nµy.

6. PhÇn 1 giíi thiÖu vÒ matlab
1. B¾t ®Çu víi Matlab
Sau khi bËt m¸y tÝnh, ®Ó khëi ®éng Matlab, tõ mµn h×nh Destop,
nh¾p ®óp trá chuét tr¸i vµo biÓu t−îng cña Matlab. trªn mµn h×nh
sÏ xuÊt hiÖn cöa sæ Command Window nh− h×nh d−íi ®©y:
H×nh 1
B¹n còng cã thÓ vµo Matlab b»ng c¸ch trªn mµn h×nh Destop bÊm chän
Start Program Matlab5.3 kÕt qu¶ mhËn ®−îc còng nh− trªn.
Ta cã thÓ trùc tiÕp thùc hiÖn c¸c phÐp tÝnh to¸n vµ ch¹y c¸c ch−¬ng tr×nh
trªn cöa sæ Command Window nµy.
VÝ dô 1: CÇn ttùc hiÖn phÐp tÝnh 201+191x32/44, tõ dÊu nh¾c trªn
Command Window ta gâ vµo nh− sau:
>> 201+191*32/44
BÊm Enter, kÕt qu¶ cho nh− d−íi ®©y:
ans =
339.9091
H×nh 2 lµ h×nh ¶nh b¹n thÊy trªn mµn h×nh.

7. H×nh 2
VÝ dô 2: NÕu b¹n muèn vÏ ®å thÞ hµm sè y=5sinx+2cos2x+0,2x víi biÕn
x ch¹y tõ -10 ®Õn 10, gia sè cña x lµ 0,1, trªn Command Window b¹n cã
thÓ gâ vµo c¸c lÖnh nh− ®−îc thÓ hiÖn trong h×nh 3 d−íi ®©y:
H×nh 3
Sau khi bÊm Enter ë dßng lÖnh cuèi cïng, ch−¬ng tr×nh ch¹y vµ
cho kÕt qu¶ lµ ®å thÞ nh− trong h×nh 4.

8. H×nh 4
NÕu muèn l−u gi÷ ch−¬ng tr×nh vÏ ®å thÞ trªn ®Ó cã thÓ tu söa hoÆc ch¹y
nhiÌu lÇn, b¹n h·y viÕt mét file ch−¬ng tr×nh ( gäi lµ M. file) nh− sau:
trªn cöa sæ Command Window bÊm chän File New M-file (h×nh 5):
H×nh 5
trªn mµn h×nh sÏ xuÊt hiÖn mét cöa sæ so¹n th¶o Editor/ Debugger víi
tªn file lµ [Untitled1] nh− trªn h×nh 6 d−íi ®©y:

9. H×nh 6
ViÕt ch−¬ng tr×nh vÏ ®å thÞ trªn mµn h×nh so¹n th¶o ®ã ( H×nh 7).
H×nh 7
Khi viªt xong ta ®Æt tªn cho file vµ cÊt nã b»ng c¸ch bÊm chän File
Save as trªn mµn h×nh Editor / Debugger ( H×nh 8). Cöa sæ
Save as xuÊt hiÖn (h×nh 9): ta gâ

10. H×nh 8
tªn file, vÝ dô dothi vµo « File name råi bÊm chän Save. Ch−¬ng tr×nh sÏ
®−îc tù ®éng cÊt vµo th− môc Work cña Matlab víi tªn lµ dothi vµ víi
®u«i mÆc ®Þnh lµ .m ( file võa cÊt sÏ lµ dothi.m).
»
H×nh 9
§Ó ch¹y ch−¬ng tr×nh trong file nµy, t¹i chç dÊu nh¾c trªn mµn h×nh
Command Window ta chØ viÖc gâ tªn file :
>> dothi

11. råi bÊm Enter.Ch−¬ng tr×nh sÏ ®−îc thùc hiÖn vµ kÕt qu¶ cho ra lµ ®å thÞ
nh− ®−îc thÓ hiÖn trªn h×nh 4.
Tr−êng hîp b¹n cÊt file .m vµo mét th− môc ngoµi, khi cÇn ch¹y ch−¬ng
tr×nh cã thÓ bÊm chän File Run Scrip, mét cöa sæ sÏ xuÊt hiÖn vµ b¹n
cã thÓ gâ ®−êng dÉn vµ tªn file vµo ®ã råi bÊm phÝm Enter.
2. C¸c kh¸i niÖm c¬ b¶n
a-C©u lÖnh vµ biÕn trong Matlab
C¸c c©u lÖnh trong Matlab th−êng cã d¹ng sau:
biÕn = biÓu thøc
Tªn biÕn ®−îc b¾t ®Çu b»ng mét ch÷ c¸i, sau ®ã cã thÓ lµ c¸c ch÷ vµ sè.
VÝ dô:
a2=4/5
Matlab chÊp nhËn tªn biÕn (còng nh− tªn hµm) cã ®Õn 19 kÝ tù vµ ph©n
biÖt ch÷ in hoa víi ch÷ in th−êng. VÝ dô : A vµ a lµ tªn hai biÕn kh¸c
nhau.
Kh«ng gièng víi mét sè phÇn mÒm lËp tr×nh kh¸c, ë ®©y biÕn kh«ng
ph¶i khai b¸o tr−íc. NÕu kh«ng viÕt tªn biÕn vµ dÊu = tr−íc biÓu thøc th×
ch−¬ng tr×nh sÏ tù ®éng t¹o tªn biÕn lµ ans ( ®øng cho ch÷ answer).
VÝ dô:
>> 4/5
ans =
0.8000
NÕu cuèi c©u lÖnh ta ®¸nh dÊu kÕt thóc ‘ ; ‘ th× c¸c phÐp tÝnh ®−îc thùc
hiÖn nh−ng kh«ng xuÊt kÕt qu¶ ra mµn h×nh. Ng−îc l¹i nÕu kh«ng gâ dÊu
kÕt thóc lÖnh th× kÕt qu¶ tÝnh ®−îc in ra mµn h×nh. VÝ dô:
>> b20=30+3^4/35
b20 =
32.3143
NÕu c©u lÖnh qu¸ dµi kh«ng thÓ viÕt hÕt ®−îc trªn mét dßng th× cã thÓ
dïng dÊu ba chÊm (...) ®Ó viÕt tiÕp trªn dßng thø hai. VÝ dô:
>> b = 22.334 - 45.12 + 89.222 – ( 123.30+330.2)/217.22 ...
+ 87.32 – 443.112 ;
Muèn viÕt lêi chó dÉn, tr−íc dßng ®ã ta gâ dÊu %. VÝ dô:
% Day la chuong trinh giai phuong trinh vi fan bËc hai.
Khi ch¹y ch−¬ng tr×nh, m¸y sÏ bá qua dßng nµy.
b. C¸c phÐp to¸n
• C¸c phÐp to¸n sè häc: nèi c¸c to¸n h¹ng trong biÓu thøc
®−îc víi
nhau. DÊu c¸c phÐp to¸n nh− sau:
+ céng
- trõ
* nh©n

12. / chia ph¶i
chia tr¸i
^ luü thõa
• C¸c phÐp to¸n quan hÖ
== b»ng
<= nhá h¬n hoÆc b»ng
>= lín h¬n hoÆc b»ng
~= kh«ng b»ng
< nhá h¬n
> lín h¬n
• C¸c phÐp to¸n l« gic
& vµ
/ hoÆc
~ kh«ng
C¸c phÐp to¸n quan hÖ vµ l« gÝc th−êng ®−îc dïng trong c¸c biªñ thøc
cña c¸c to¸n tö ®iÒu khiÓn nh− if, while.
c. Sè dïng trong Matlab
Matlab dïng sè thËp ph©n truyÒn thèng víi sè ch÷ sè thËp ph©n tuú chän.
B¹n còng cã thÓ dïng sè d−íi d¹ng luü thõa cña 10 vµ sè cã ®¬n vÞ phøc.
D−íi ®©y lµ mét sè vÝ dô vÒ c¸c sè hîp thøc dïng trong Matlab:
4 57 -180.1122
3.09837412 12.6529E4 20.2908e-2
12i -23.1261i 5e2i
d- NhËp sè liÖu tõ bµn phÝm
Dïng lÖnh input víi qui c¸ch viÕt nh− sau:
a=input(‘ H·y nhËp gi¸ trÞ cña a : a = ‘)
Khi ch¹y ch−¬ng tr×nh m¸y sÏ dõng ®Ó ®îi ta gâ vµo tõ bµn phÝm gi¸ trÞ
cña a, sau ®ã bÊm Enter.
e. In kÕt qu¶ ra mµn h×nh: cã hai c¸ch
C¸ch 1 : Kh«ng gâ dÊu kÕt thóc ( ; ) ë cuèi c©u lÖnh. Khi ch¹y kÕt qu¶
tÝnh ®−îc tù ®éng in ra trªn mµn h×nh.
VÝ dô:
>> x=12+6*sin(pi/7)
x=
14.6033
C¸ch 2: dïng lÖnh disp
>> x=12+6*sin(pi/7);
disp(x)
14.6033
f. Ma trËn

13. Ma trËn ®−îc biÓu thÞ trong dÊu ngoÆc vu«ng, mçi phÇn tö trªn mét hµng
®−îc c¸ch nhau b»ng c¸c « trèng hoÆc dÊu phÈy (,), cßn mçi hµng ®−îc
ng¨n c¸ch bëi dÊu chÊm phÈy (;).
VÝ dô : viÕt ma trËn A gåm 3 hµng 3 cét trªn mµn h×nh Command
Window
>> A=[ 1 2 3 ; 4 5 6 ; 7 8 9]
A=
1 2 3
4 5 6
7 8 9
Tr−êng hîp ma trËn qu¸ lín ta cã thÓ viÕt mçi hµng cña ma trËn trªn mét
dßng nh− sau:
B=[1 2 3 4
5 6 7 8
9 10 11 12 ] ;
C¸c phÇn tö cña ma trËn cã thÓ lµ c¸c biÓu thøc. VÝ dô:
C=[ -1 2*3/5 2.2^3 (12+34/7)/3 ]
C=
-1.0000 1.2000 10.6480 5.6190
g. Sè phøc vµ ma trËn phøc
Matlab cã thÓ thùc hiÖn ®−îc c¸c phÐp to¸n vÒ sè phøc. Sè phøc
®−îc biÓu thÞ nhê hµm i vµ j. VÝ dô viÕt sè phøc z dïng i vµ j nh−
d−íi ®©y cho kÕt qu¶ nh− nhau:
z = 4+5*i
hoÆc z = 4+5*j
Mét vÝ dô kh¸c vÒ sè phøc ®−îc viÕt d−íi d¹ng e mò:
w =r* exp(i*theta)
Ma trËn cã c¸c phÇn tö lµ sè phøc ®−îc viÕt nh− sau:
A=[ 3+2*i 4-9*i ; 12+i 7-6*i ]
3. C¸c hµm to¸n häc
a. C¸c hµm l−îng gi¸c
- sin : sin
- cos : cosin
- tan : tang
- asin : arcsin
- acos : arccosin
- atan : arctang
- atan2 : arctan gãc phÇn t−
- sinh : sin hypecb«lic
- cosh : cosin hypecb«lic
- tanh : tang hypecb«lic

14. - asinh : sin hypecb«lic ng−îc
- acosh : cosin hypecb«lic ng−îc
- atanh : tang hypecb«lic ng−îc
VÝ dô 1:
a=1.223;
b=sin(a)
KÕt qu¶ cho:
b=
0.9401
VÝ dô 2:
c=[1.22 -0.96 1.17 ];
d=cos(c)
KÕt qu¶ cho:
d=
0.3436 0.5735 0.3902
b. C¸c hµm to¸n s¬ cÊp
- abs : gi¸ trÞ tuyÖt ®èi hoÆc m« ®un cña sè phøc
- angle : gãc pha
- real : phÇn thùc cña sè phøc
- imag: phÇn ¶o
- sqrt : c¨n bËc hai
- conj : sè phøc liªn hîp
- round : lµm trßn ®Õn sè nguyªn gÇn nhÊt
- fix : lµm trßn h−íng vÒ zÎo
- sign : hµm xÐt dÊu
- gcd : ø¬c sè chung lín nhÊt
- lom : Béi sè chung nhá nhÊt
- exp : hµm e mò
- log : logarit c¬ sè tù nhiªn
- log10 : logarit c¬ sè 10
VÝ dô 1:
a=2+5*i;
md= abs(a)
arg= angle(a)
KÕt qu¶ cho:
md =
5.3852
arg =
1.1903
4. C¸c thao t¸c ®Æc biÖt trªn ma trËn

15. - T¹o ma trËn hµng
>>t=0: 0.5: 3
t=
0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000
>> v= -2: 3
v=
-2 -1 0 1 2 3
- LÊy ra mét ma trËn con tõ mét ma trËn ®∙ cho
VÝ dô: Cho ma trËn c
>> c=[1 2 3 4 ; 5 6 7 8; 9 10 11 12]
c=
1 2 3 4
5 6 7 8
9 10 11 12
LÊy ra mét ma trËn con e tõ ma trËn c nh− sau:
>> e=c(1:2,2: 4)
e=
2 3 4
6 7 8
HoÆc vÝ dô kh¸c: lÊy ra mét ma trËn cét t−¬ng øng víi cét thø 3 cña ma
trËn c
>> f=c(:,3)
f=
3
7
11
LÊy ra mét ma trËn hµng gåm 3 phÇn tö cuèi cña hµng thø 3:
>>g=c(3,2:4)
g=
10 11 12

16. - T¹o ma trËn cã cì lín h¬n tõ c¸c ma trËn nhá
VÝ dô: t¹o ma trËn h tõ hai ma trËn e vµ g ë trªn
>> h=[e ; g]
h=
2 3 4
6 7 8
10 11 12
VÝ dô kh¸c: t¹o ma trËn k tõ ma trËn h vµ ma trËn cét f
>> k= [ h f ]
k=
2 3 4 3
6 7 8 7
10 11 12 11
- T¹o mét sè ma trËn ®Æc biÖt
+ VÕt cña ma trËn : Dïng lÖnh diag ®Ó t¹o mét ma trËn cét mµ
c¸c phÇn tö cña nã lµ c¸c phÇn tö n»m trªn ®−êng chÐo cña ma trËn cho
tr−íc. VÝ dô: muèn cã vÕt cña ma trËn h ë trªn ta lµm nh− sau:
>> ch=diag(h)
ch =
2
7
12
+ Ma trËn ®−êng chÐo
Còng dïng lÖnh diag t¹o ma trËn ®−êng chÐo tõ mét ma trËn cét hoÆc ma
trËn hµng cho tr−íc.
VÝ dô: t¹o ma trËn ®−êng chÐo tõ ma trËn cét ch ë trªn
>>C=diag(ch)
C=
2 0 0
0 7 0
0 0 12
+ Ma trËn ®¬n vÞ : Dïng hµm eye
VÝ dô: §Ó t¹o ma trËn ®¬n vÞ cã 4 hµng 4 cét ta viÕt nh− sau:
>> I=eye(4)

17. I=
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
+ Ma trËn mµ c¸c phÇn tö ®Òu lµ c¸c sè 0 hoÆc sè 1:
Dïng hµm zeros vµ hµm ones.
VÝ dô:
>> K=zeros(3,4)
K=
0 0 0 0
0 0 0 0
0 0 0 0
>>M=ones(2,2)
M=
1 1
1 1
- §¶o ma trËn
Dïng hµm fliplr ®Ó ®¶o ma trËn tõ tr¸i sang ph¶i vµ hµm flipud ®¶o ma
trËn tõ trªn xuèng d−íi.
VÝ dô : Cho ma trËn M cì 4x4 råi tiÕn hµnh ®¶o nh− d−íi ®©y
>> M=[1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]
M=
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
>> Mtf=fliplr(M) % Dao tu trai sang phai
Mtf =
4 3 2 1
8 7 6 5
12 11 10 9
16 15 14 13
>> Mtd=flipud(M) % Dao tu tren xuong duoi
Mtd =

18. 13 14 15 16
9 10 11 12
5 6 7 8
1 2 3 4
5. Thùc hiÖn C¸c phÐp tÝnh trªn ma trËn
a- C¸c phÐp tÝnh tiªu chuÈn
Gi¶ sö cho a lµ ma trËn vu«ng cì 4x4
a=[1 3 -4 5; 2 -1 2 0 ; 4 6 -1 1; 0 1 3 5]
a=
1 3 -4 5
2 -1 2 0
4 6 -1 1
0 1 3 5
- Ma trËn chuyÓn vÞ
Ma trËn chuyÓn vÞ cña a lµ ac ®−îc x¸c ®Þnh nh− sau:
ac=a'
ac =
1 2 4 0
3 -1 6 1
-4 2 -1 3
5 0 1 5
- Céng ma trËn : hai ma trËn ph¶i cïng cì. Ta tÝnh tæng cña hai
ma trËn a vµ ac nh− sau:
at=a+ac
at =
2 5 0 5
5 -2 8 1
0 8 -2 4
5 1 4 10
- Céng mét sè víi ma trËn:
Matlab coi sè ®ã nh− mét ma trËn cïng cì víi ma trËn ®−îc céng, mçi
phÇn tö cña ma trËn b»ng chÝnh sè ®ã. VÝ dô: céng sè lµ 7 víi ma trËn at
ë trªn ta ®−îc ma trËn cs.
s =7;
cs=s+at
cs =
9 12 7 12
12 5 15 8
7 15 5 11
12 8 11 17
- Nh©n ma trËn víi mét sè

19. VÝ dô: Nh©n sè 3 víi ma trËn a ë trªn
>> t=3*a
t=
3 9 -12 15
6 -3 6 0
12 18 -3 3
0 3 9 15
- Nh©n ma trËn víi ma trËn
§iÒu kiÖn ®Ó hai ma trËn nh©n ®−îc víi nhau lµ sè cét cña ma trËn thø
nhÊt ph¶i b»ng sè hµng cña ma trËn thø hai. VÝ dô ta nh©n ma trËn b
d−íi ®©y víi ma trËn a:
>> b=[3 7 0 9];
>> tich=b*a
tich =
17 11 29 60
VÝ dô n÷a lµ ta nh©n ma trËn a víi ma trËn chuyÓn vÞ cña b:
>> tich2=a*b'
tich2 =
69
-1
63
52
- Chia ma trËn
Ma trËn x= AB víi ®iÒu kiÖn : A*x=B (*)
VÝ dô:
A=[ 2 1 9 7; 1 3 8 5; 5 3 4 2; 9 0 6 6]
A=
2 1 9 7
1 3 8 5
5 3 4 2
9 0 6 6
B=[12; 2; -6; 8 ]'
B=
12
2
-6
8
x= AB

20. x=
0.1026
-6.2051
4.8718
-3.6923
Thö l¹i xem A*x cã b»ng B kh«ng:
A*x
ans =
12.0000
2.0000
-6.0000
8.0000
KÕt qu¶ ®óng b»ng vÐc t¬ B
(còng cã thÓ dïng phÐp chia ph¶i / nh−ng ph¶i thay A vµ B b»ng c¸c ma
trËn chuyÓn vÞ t−¬ng øng, tøc B’/A’, vµ kÕt qu¶ lµ mét ma trËn hµng ®óng
b»ng ma trËn chuyÓn cña nghiÖm x ®· tÝnh ë trªn).
- Ma trËn nghÞch ®¶o : Dïng hµm inv
VÝ dô: TÝnh ma trËn nghÞch ®¶o cña ma trËn A ë trªn
gäi An lµ ma trËn nghÞch ®¶o cña ma trËn A th×:
>> An=inv(A)
An =
0.4615 -0.6154 0.4615 -0.1795
-2.9231 3.2308 -1.9231 1.3590
3.9231 -4.2308 2.9231 -2.0256
-4.6154 5.1538 -3.6154 2.4615
Thö t×m nghiÖm x tõ ph−¬ng tr×nh (*) khi dïng ma trËn nghÞch ®¶o:
Ta cã nghiÖm x ®−îc viÕt nh− sau: x=A-1.B
Gâ vµo dßng lÖnh sau:
X=An*B
KÕt qu¶ cho:
X=
0.1026
-6.2051
4.8718
-3.6923
- §Þnh thøc cña ma trËn
§Þnh thøc cña ma trËn vu«ng ®−îc tÝnh nhê hµm det. VÝ dô tÝnh ®Þnh thøc
D cña ma trËn A ë trªn:
>> D=det(A)

21. D=
-39
- Nh©n v« h−íng, nh©n cã h−íng vÐc t¬
Cho hai vÐc t¬ m vµ n nh− sau:
m=[1 1 3]; n=[4 2 0];
TÝch v« h−íng cña m vµ n: dïng hµm dot
vh=dot(m,n)
vh = 6
TÝch cã h−íng cña m vµ n: dïng hµm cross
ch=cross(m,n)
ch = -6 12 -2
Cßn tÝch cã h−íng cña n vµ m:
ch2=cross(n,m)
ch2 = 6 -12 2
b- C¸c phÐp tÝnh phÇn tö - phÇn tö cña ma trËn
C¸c phÐp tÝnh nµy rÊt tiÖn Ých vµ ®−îc ph©n biÖt víi c¸c phÐp tÝnh tiªu
chuÈn trªn ma trËn b»ng dÊu chÊm ( . ) ®−îc ®Æt tr−íc c¸c dÊu phÐp tÝnh.
VÝ dô: X.^Y, X.*Y, hay X.Y. NÕu X vµ Y lµ c¸c ma trËn ( hay vÐc t¬)
c¸c phÇn tö cña X sÏ ®−îc n©ng lªn luü thõa hoÆc ®−îc nh©n , chia bëi
c¸c phÇn tö t−¬ng øng cña ma trËn Y. DÏ thÊy lµ ma trËn X vµ Y ph¶i
cïng cì.
- Luü thõa c¸c phÇn tö ma trËn
VÝ dô:
>> x=[1 2 ; 3 4]
x=
1 2
3 4
>> y=[ 3 4; 1 2]
y=
3 4
1 2
>> x.^y
ans =
1 16
3 16
x=

22. 1 2
3 4
NÕu y kh«ng ph¶i lµ ma trËn mµ lµ mét sè, vÝ dô y=2, th× kÕt qu¶ nh−
sau:
>> x.^2
ans =
1 4
9 16
- Nh©n phÇn tö ma trËn
VÝ dô
>> x.*y
ans =
3 8
2 8
- Chia phÇn tö ma trËn
VÝ dô;
>> x./y
ans =
0.3333 0.5000
3.0000 2.0000
6. C¸c hµm thùc hiÖn c¸c phÐp tÝnh víi ®a thøc
- Hµm poly : X¸c ®Þnh ®a thøc khi biÕt tr−íc nghiÖm
Quy c¸c viÕt p=poly(b)
trong ®ã b lµ mét ma trËn hµng.
KÕt qu¶ sÏ cho ra lµ mét ma trËn hµng mµ mçi phÇn tö cña nã lµ mét hÖ
sè cña mét ®a thøc cã nghiÖm lµ c¸c phÇn tö cña ma trËn b ( theo sè mò
gi¶m dÇn).
VÝ dô:
b=[2 1 -4 3];
p=poly(b)
p=
1 -2 -13 38 -24
Theo kÕt qu¶ trªn th× c¸c sè 2, 1, -4 vµ 3 lµ nghiÖm cña ®a thøc :

23. x4- 2x3 - 13x2 + 38x - 24 = 0
- Hµm roots : X¸c ®Þnh nghiÖm cña ®a thøc
Quy c¸ch viÕt : a=roots(b)
trong ®ã b lµ ma trËn hµng víi c¸c phÇn tö lµ c¸c hÖ sè cña ®a thøc (theo
sè mò gi¶m dÇn). KÕt qu¶ cho ra lµ mét ma trËn cét mµ c¸c phÇn tö lµ
nghiÖm cña ®a thøc.
VÝ dô: Thö t×m l¹i nghiÖm cña ®a thøc trªn. Ta viÕt c¸c lÖn nh− sau:
p=[ 1 -2 -13 38 -24 ];
r=roots(p)
r=
-4.0000
3.0000
2.0000
1.0000
Ta thÊy kÕt qu¶ hoµn toµn chÝnh x¸c.
- Hµm conv : Dïng nh©n ®a thøc.
Quy c¸ch viÕt: a=conv(b,c) trong ®ã b,c lµ hai ma trËn hµng cã c¸c phÇn
tö lµ c¸c hÖ sè cña c¸c ®a thøc cÇn nh©n. KÕt qu¶ cho ra lµ ma trËn a cã
c¸c phÇn tö lµ hÖ sè cña ma trËn tÝch.
VÝ dô : cÇn nh©n hai ®a thøc x3+2x2+6 vµ 3x4-6x2+5x-10 ta lµm nh− sau:
b=[1 2 0 6];
c=[3 0 -6 5 -10];
a=conv(b,c)
a=
3 6 -6 11 0 -56 30 -60
VËy ®a thøc tÝch lµ: 3x7+ 6x6- 6x5 + 11x4 - 56x2 + 30x – 60
- Hµm deconv : Dïng chia hai ®a thøc
Qui c¸ch viÕt nh− sau: [ m , n] = deconv(p,q)
víi p vµ q lµ hai ma trËn hµng cã c¸c phÇn tö lµ c¸c hÖ sè cña ®a thøc bÞ
chia vµ ®a thøc chia, cßn c¸c phÇn tö cña ma trËn m,n lµ c¸c hÖ sè cña ®a
thøc th−¬ng vµ phÇn d−.
VÝ dô : Ta thö chia ngay ®a thøc tÝch võa cã ë trªn cho ®a thøc cã c¸c hÖ
sè lµ c¸c phÇn tö cña ma trËn c, tøc ®a thøc: 3x4-6x2+5x-10.
a=[3 6 -6 11 0 -56 30 -60];
c=[3 0 -6 5 -10];
[b,d]=deconv(a,c)

24. b=
1 2 0 6
d=
0 0 0 0 0 0 0 0
Ta thÊy kÕt qu¶ lµ hoµn toµn ®óng.
7. c¸c Hµm dïng ph©n tÝch d÷ liÖu
C¸c hµm t×m gi¸ trÞ cùc ®¹i, cùc tiÓu vµ trung b×nh
- Hµm max : T×m gi¸ trÞ lín nhÊt
Qui c¸ch viÕt ln=max(a)
víi a lµ ma trËn hµng. KÕt qu¶ cho ra lµ mét phÇn tö cã gi¸ trÞ lín nhÊt
cña a
VÝ dô:
a=[ 10 2 1 -30 23 8];
ln=max(a)
ln =
23
- Hµm min : t×m gi¸ trÞ cùc tiÓu
VÝ dô:
bn=min(a)
bn =
-30
bn=mi
- Hµm mean : T×m gi¸ trÞ trung b×nh
VÝ dô:
tb=mean(a)
tb =
2.3333
NÕu a lµ mét ma trËn cã nhiÒu hµng nhiÒu cét th× c¸c gi¸ trÞ max, min
hoÆc trung b×nh sÏ lµ c¸c gi¸ trÞ t−¬ng øng ®èi víi c¸c cét cña ma trËn.
VÝ du :
>>b=[1 2 3; 4 5 6 ; 7 8 9]
b=
1 2 3
4 5 6
7 8 9
>>ln=max(b)
ln =
7 8 9

25. >>bn=min(b)
bn =
1 2 3
>>tb=mean(b)
tb =
4 5 6
- Hµm sum : dïng tÝnh tæng
VÝ dô: TÝnh tæng c¸c phÇn tö cña ma trËn a nh− sau
T=sum(a)
T=
26
- Hµm diff : TÝnh gi¸ trÞ sai kh¸c cña hai sè ®øng liÒn nhau. Qui c¸ch
viÕt:
s=diff(x)
víi x lµ mét ma trËn hµng hoÆc cét.
VÝ dô:
>>x=[ 1.2 1.4 1.8 2.1 3 ];
>> s=diff(x)
s=
0.2000 0.4000 0.3000 0.9000
Ta dÔ dµng thÊy r»ng hµm diff nµy cã thÓ dïng ®Ó tÝnh gÇn ®óng ®¹o
hµm.
NÕu x lµ mét ma trËn b×nh th−êng th× qu¸ tr×nh tÝnh sÏ ®−îc thùc hiÖn
theo thø tù c¸c cét.
- Hµm Interp1 : Dïng t×m c¸c gi¸ trÞ bÞ khuyÕt.
VÝ dô: §· biÕt gi¸ trÞ cña hµm y=x3-3x+4 t¹i c¸c ®iÓm cã x=0,1,2,3,4 vµ
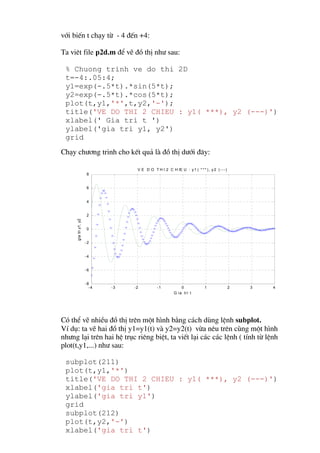
5. H·y x¸c ®Þnh gi¸ trÞ cña y t¹i c¸c ®iÓm cã x= 0,3, 0,5, ..., 4.2, 4,8.
Ta viÕt c¸c lÖnh nh− sau:
x1=0:5;
y1=x1.^3-3*x1+4;
x2=[0 .3 .5 1.2 1.4 2.1 3.3 4.2 4.8 5];
y2=interp1(x1,y1,x2,'cubic')
plot(x1,y1,'ro',x2,y2,'b+')
KÕt qu¶ cho ë d¹ng sè vµ ®å thÞ d−íi ®©y
y2 =
Columns 1 through 7
4.0000 2.7700 2.2500 2.2240 2.5920 7.0330 30.1210

26. Columns 8 through 10
65.6800 100.4800 114.0000
§ã lµ 10 gi¸ trÞ cña y øng víi 10 gi¸ trÞ cña x ( trong ch−¬ng tr×nh tÝnh lµ
x2). Cßn ®å thÞ sÏ cho thÊy sù ppï hîp cña c¸c kÕt qu¶ nµy: C¸c ®iÓm vÏ
b»ng dÊu ‘+’ lµ biÓu thÞ c¸c ®iÓm cÇn t×m, cßn c¸c ®iÓm vÏ b»ng dÊu ‘o’
lµ t−¬ng øng c¸c ®iÓm ®· cho.
120
100
80
60
40
20
0
0 1 2 3 4 5
8. Hµm cña hµm
Cã nhiÒu hµm trong Matlab kh«ng chØ lµm viÖc víi c¸c ma trËn sè mµ
cßn lµm viÖc víi c¸c hµm to¸n. C¸c hµm cña hµm nµy bao gåm c¸c hµm
dïng ®Ó tÝnh tÝch ph©n, gi¶i c¸c ph−¬ng tr×nh phi tuyÕn vµ gi¶i c¸c
ph−¬ng tr×nh vi ph©n.
a. Hµm dïng ®Ó tÝch ph©n sè: hµm quad hoÆc quad8
VÝ dô: CÇn tÝnh tÝch ph©n cña hµm f(x) = 3+sin2x/(4+2cosx) víi cËn tõ
0 ®Õn 4, ta tiÕn hµnh nh− sau:
ViÕt mét file hµm cã tªn tfan1.m nh− d−íi ®©y:
function f=tfan1(x)
f=3+sin(2*x)/(4+2*cos(x));
vµ mét file chÝnh cã tªn tfan.m:
tf=quad8('tfan1',0,4)
Ch¹y ch−¬ng tr×nh kÕt qu¶ cho gi¸ trÞ cña tÝch ph©n:
tf =

27. 12.0517
b. Hµm ®Ó t×m nghiÖm ph−¬ng tr×nh phi tuyÕn vµ c¸c hµm tèi
−u
- Hµm fzero : x¸c ®Þnh nghiÖm cña hµm mét biÕn.
- Hµm fmin : tÝnh gi¸ trÞ cùc tiÓu cña hµm mét biÕn.
- Hµm fmins : tÝnh c¸c gi¸ trÞ cùc tiÓu cña hµm nhiÒu biÕn
VÝ dô: Dïng hµm fzero t×m nghiÖm cña ph−¬ng tr×nh sau t¹i vÞ trÝ gÇn
x=1 :
y=2- 6sinx / (1+x);
Ta viÕt file hµm nghiem1.m nh− sau:
function y=nghiem(x)
y=2-6*sin(x)./(1+x);
Sau ®ã viÕt file chÝnh nghiem.m:
x1=fzero('nghiem1',1)
Ch¹y ch−¬ng tr×nh chÝnh, kÕt qu¶ cho trªn mµn h×nh nh− sau:
Zero found in the interval: [0.36, 1.4525].
x1 =
0.5385
§Ó thö l¹i, ta thay x=x1 vµo ph−¬ng tr×nh ban ®Çu ®Ó xem kÕt qu¶ hai vÕ
cã b»ng 0 hay kh«ng.
y=2-6*sin(.5385)/(1+.5385)
y=
-6.0516e-005
Ta thÊy y~ 0 vµ cã thÓ nãi kÕt qu¶ ®ñ chÝnh x¸c.
c. Hµm ®Ó gi¶i ph−¬ng tr×nh vi ph©n : hµm ode23 vµ ode34
VÝ dô: Gi¶i ph−¬ng tr×nh vi ph©n Van de Pol cã d¹ng nh− sau:
x’’+( x2- 1 ) x’+ x=0
Ta viÕt l¹i ph−¬ng tr×nh trªn d−íi d¹ng hÖ ph−¬ng tr×nh vi ph©n bËc nhÊt:
x1’= x1(1- x22 ) - x2
x2’= x1
ViÕt mét file hµm mang tªn ftvf.m m« t¶ hÖ ph−¬ng tr×nh vi ph©n:
function xc=ftvf(t,x)

28. xc=zeros(2,1);
xc(1)=x(1).*(1-x(2).^2)-x(2);
xc(2)=x(1);
ViÕt file chÝnh cã tªn ftvf0.m nh− d−íi ®©y:
t0=0; t1=20;% Thoi diem dau va cuoi
x0=[0 .2]; % Dieu kien ban dau
[t,x]=ode23('ftvf',t0,t1,x0);
plot(t,x)
Ch¹y ch−¬ng tr×nh kÕt qu¶ cho d−íi d¹ng ®å thÞ nh− d−íi ®©y:
3
2
1
0
-1
-2
-3
0 5 10 15 20
9. C¸c to¸n tö ®iÒu khiÓn
Còng nh− c¸c phÇn mÒm lËp tr×nh kh¸c, c¸c to¸n tö ®iÒu khiÓn còng cã
trong Matlab. §ã lµ to¸n tö vßng lÆp for, while vµ to¸n tö lùa chän if.
- To¸n tö for
D¹ng chung cña to¸n tö nµy ®−îc viÕt nh− sau:
for biÕn = biÓu thøc
c¸c c©u lÖnh
end
BiÓu thøc ë ®©y th−êng cã d¹ng m:n hoÆc m:i:n, trong ®ã m, n lµ
gi¸ trÞ ®Çu vµ cuèi, cßn i lµ gia sè.
VÝ dô:
for k=1: n
a(k)=sin(k*pi/5);
b(k)=cã(k*pi/5);
end

29. - To¸n tö while
D¹ng chung cña lÖnh vßng lÆp nµy cã d¹ng sau:
while biÓu thøc
c¸c c©u lÖnh
end
BiÓu thøc ë ®©y lµ biÓu thøc quan hÖ.
VÝ dô:
d=1;
while d>0.001
z1=z2-sin(z2)/(z2+2);
d=abs(z2-z1);
z2=z1;
end
- To¸n tö ®iÒu kiÖn if
To¸n tö cã d¹ng chung nh− sau:
if biÓu thøc
c¸c c©u lÖnh
elseif biÓu thøc
c¸c c©u lÖnh
...
...
else
c¸c c©u lÖnh
end
Còng nh− ®èi víi to¸n tö while biÓu thøc ë ®©y còng lµ biÓu
thøc quan hÖ.
VÝ dô:
for k=1: n
for p=1: m
if k= =p
z(k,p)=1;
elseif k<p
z(k,p)=-1 ;
else
z(k,p)=0;
end
end
end
- C©u lÖnh Break
LÖnh Break cho phÐp tho¸t ra khái vßng lÆp.
VÝ dô:
k=input(' k=');
if k>0
break
else

30. a=5*k+4
end
10. c¸c lo¹i file dïng trong matlab
Cã hai lo¹i file lµ M-File vµ file d÷ liÖu (data file)
C¸c file cã chøa c¸c lÖnh cña Matlab ®−îc gäi lµ M-
file . Së dÜ gäi lµ M- file v× phÇn më réng cña c¸c file
nµy lµ .m.
Cã hai lo¹i M- file lµ script file vµ function file (file hµm)
Script File
Khi Script ®−îc kÝch ho¹t Matlab ®¬n gi¶n thùc hiÖn c¸c lÖnh t×m thÊy
trong file. C¸c c©u lÖnh trong file nµy th× ho¹t ®éng trªn toµn bé c¸c d÷
liÖu trong Workspace.
VÝ dô : file lg.m d−íi ®©y lµ mét script file:
% File dung tinh ham luong giac va ve do thi
f1=0:2*pi/60;
a=3*sin(f1)+4.5*cos(f1+.6);
plot(f1,a)
Sau khi tÝnh to¸n vµ vÏ ®ß thÞ xong c¸c biÕn f1 vµ a vÉn cßn l−u trong
workspace
Function File
Lµ mét M-File cã chøa tõ function t¹i vÞ trÝ ®Çu tiªn trªn dßng ®Çu cña
file. Víi function file, c¸c biÕn ®−îc ®Þnh nghÜa vµ ho¹t ®éng chØ trong
ph¹m vi file, chø kh«ng cã tÝnh toµn côc nh− trong script file. Function
file rÊt tiÖn Ých trong viÖc më réng thªm kh¶ n¨ng cña Matlab, cô thÓ lµ
t¹o thªm ®−îc c¸c Matlab file míi.
D−íi ®©y lµ mét vÝ dô vÒ function file ®−îc t¹o ®Ó gi¶i ph−¬ng tr×nh bËc
hai, tªn file lµ ftb2.m :
function [x1 , x2] = ftb2(a,b,c)
% File ham nay dung de giai Fuong tr×nh bac hai : ax^2+bx+c=0
% voi a, b, c la cac hang so cho truoc. Cac nghiem lµ x1 va x2
delta=b^2-4*a*c;
x1=(-b+sqrt(delta)/(2*a);
x2=(-b-sqrt(delta)/(2*a);
Hµm nµy dïng ®Ó gi¶i ph−¬ng tr×nh bËc hai víi lÖnh gäi ra lµ:
[nghiem1, nghiem2] = ftb2(10,-6.5,-3.5);
File d÷ liÖu ( data file)
Ta cã thÓ ghi sè liÖu vµo mét file gäi lµ file sè liÖu víi phÇn më réng lµ
.dat. Khi cÇn file cã thÓ ®−îc gäi ra.

31. D−íi ®©y lµ vÝ dô vÒ t¹o vµ gäi file sè liÖu:
Gi¶ sö ta cã mét ma trËn hµng a nh− sau:
>>a=1:8
a=
1 2 3 4 5 6 7 8
Giê ta muèn ghi c¸c gi¸ trÞ cña ma trËn a vµo mét file d÷ liÖu cã tªn lµ
sl1.dat, ta dïng lÖnh save víi qui c¸ch viÕt nh− sau:
>> save sl1.dat a -ascii
Khi ®ã ma trËn a ®· ®−îc l−u trong fil sl1.dat. NÕu muèn gäi ra c¸c sè
liÖu nµy vµ g¸n cho cho nã mét tªn biÕn míi, vÝ dô lµ x, ta dïng lÖnh
load víi qui c¸ch viÕt nh− sau:
>>load sl1.dat
>> x=sl1
x=
1 2 3 4 5 6 7 8
11. Xö lÝ tÝn hiÖu
Matlab cã mét sè hµm dïng ®Ó xö lÝ tÝn hiÖu sè d−íi ®©y:
abs - gi¸ trÞ (m« ®un) cña sè phøc
angle – gãc pha
conv - tÝch chËp ( convolution)
deconv – ( deconvotution)
fft - biÕn ®æi Fu ri ª nhanh
ift - biÕn ®æi ng−îc Fu ri ª
fftshift
VÝ dô: cho x lµ mét ma trËn cét nh− sau:
x=[ 4 3 7 -9 1 0 0 0 ]’ ;
BiÕn ®æi Fu ri ª nhanh cña x ®−îc viÕt nh− sau:
y=fft(x)
KÕt qu¶ cho nh− d−íi ®©y:
y=
6.0000
11.4853 + 2.7574i
-2.0000 +12.0000i
-5.4853 -11.2426i
18.0000
-5.4853 +11.2426i
-2.0000 -12.0000i
11.4853 - 2.7574i

32. 12. vÏ ®å thÞ
Matlab rÊt m¹nh víi viÖc vÏ ®å thÞ. D−íi ®©y tr×nh bµy c¸ch vÏ ®å thÞ
trong kh«ng gian hai chiÒu (2D) vµ ba chiÒu (3D).
a.VÏ ®å thÞ 2D
VÏ c¸c ®−êng cong th«ng th−êng:
Dïng lÖnh plot víi qui c¸ch viÕt nh− sau:
plot(x,y)
trong ®ã x vµ y lµ c¸c ma trËn hµng (hoÆc cét ) cïng cì. Matlab sÏ vÏ ra
mét ®−êng cong cña y theo x.
NÕu b¹n muèn chän mµu vµ kiÓu nÐt vÏ cho ®−¬ng cong cã thÓ lµm theo
vÝ dô sau:
plot(x,y, 'r*')
Khi ch¹y, Matab sÏ cho b¹n ®−êng cong t¹o bëi c¸c dÊu *** vµ cã mµu
®á (ch÷ r ®øng cho tõ red trong tiÕng Anh, nghÜa lµ ®á).
D−íi ®©y lµ b¶ng kÝ hiÖu mµu vµ kiÓu nÐt vÏ dïng khi vÏ ®å thÞ:
BiÓu t−îng Mµu s¾c BiÓu t−îng Lo¹i ®−êng nÐt
y Vµng . §iÓm
m §á t−¬i ° Vßng trßn
c Xanh l¸ m¹ × DÊu nh©n
r §á + DÊu céng
g Xanh l¸ c©y ∗ DÊu sao
b Xanh n−íc biÓn - NÐt liÒn
w Tr¾ng : NÐt chÊm
k §en -- NÐt ®øt
-. NÐt chÊm g¹ch
Còng cã thÓ vÏ nhiÒu ®−êng cong trªn cïng mét hÖ trôc to¹ ®é.
VÝ dô: lÖnh vÏ sau sÏ cho 3 ®−êng cong kh¸c nhau trªn mét h×nh:
plot(x1,y1,’r *’,x2,y2,’g+’x3,y3,’w -‘)
NÕu b¹n muèn ®Æt tªn cho ®å thÞ h·y dïng lÖnh title.
VÝ dô: title(' Do thi 1 ‘)
B¹n còng cã thÓ ®Æt tªn cho c¸c trôc to¹ ®é x vµ y b»ng c¸ch dïng lÖnh
xlabel
vµ ylabel .
VÝ dô:
xlabel('x - m');
ylabel('y - m/s ');
Cßn ®Ó t¹o l−íi trªn h×nh vÏ dïng lÖnh grid.
Cô thÓ ta lµm mét vÝ dô d−íi ®©y:
VÏ trªn cïng hÖ trôc to¹ ®é ®å thÞ hai hµm sè sau
y1=e-5tsin5t ; y2= e-5t cos5t;

33. víi biÕn t ch¹y tõ - 4 ®Õn +4:
Ta viªt file p2d.m ®Ó vÏ ®å thÞ nh− sau:
% Chuong trinh ve do thi 2D
t=-4:.05:4;
y1=exp(-.5*t).*sin(5*t);
y2=exp(-.5*t).*cos(5*t);
plot(t,y1,'*',t,y2,'-');
title('VE DO THI 2 CHIEU : y1( ***), y2 (---)')
xlabel(' Gia tri t ')
ylabel('gia tri y1, y2')
grid
Ch¹y ch−¬ng trinh cho kÕt qu¶ lµ ®å thÞ d−íi ®©y:
V E D O T H I 2 C H IE U : y 1 ( * * * ) , y 2 ( - - - )
8
6
4
2
gia tri y1, y2
0
-2
-4
-6
-8
-4 -3 -2 -1 0 1 2 3 4
G i a tr i t
Cã thÓ vÏ nhiÒu ®å thÞ trªn mét h×nh b»ng c¸ch dïng lÖnh subplot.
VÝ dô: ta vÏ hai ®å thÞ y1=y1(t) vµ y2=y2(t) võa nªu trªn cïng mét h×nh
nh−ng l¹i trªn hai hÖ trôc riªng biÖt, ta viÕt l¹i c¸c c¸c lÖnh ( tÝnh tõ lÖnh
plot(t,y1,...) nh− sau:
subplot(211)
plot(t,y1,'*')
title('VE DO THI 2 CHIEU : y1( ***), y2 (---)')
xlabel('gia tri t')
ylabel('gia tri y1')
grid
subplot(212)
plot(t,y2,'-')
xlabel('gia tri t')

34. ylabel('gia tri y2')
grid
V E D O T H I 2 C H IE U : y1 ( * * * ), y2 (---)
10
5
gia tri y1
0
-5
-1 0
-4 -3 -2 -1 0 1 2 3 4
g i a tri x
10
5
gia tri y2
0
-5
-4 -3 -2 -1 0 1 2 3 4
g i a tri x
VÏ ®å thÞ ®éc cùc Dïng lÖnh polar
VÝ dô: vÏ ®å thÞ hµm y=4e-4t víi t=0:2pi/3
Ta viÕt ch−¬ng tr×nh vÏ nh− sau:
t=0:pi/20:2*pi/3;
r=4*exp(-4*t);
polar(t,r)
KÕt qu¶ cho ra nh− d−íi ®©y:
90
4
120 60
3
150 2 30
1
180 0
210 330
240 300
270

35. VÏ §å thÞ d¹ng thanh (Bar).
§å thÞ bar biÓu diÔn gi¸ trÞ cña mét vÐc t¬ hay mét ma trËn d−íi d¹ng
c¸c thanh th¼ng ®øng hay n»m ngang. Bar(y) biÓu diÔn c¸c phÇn tö cña
vÐc t¬ y nÕu y lµ mét vÐc t¬. NÕu y lµ mét ma trËn, mét nhãm thanh sÏ
biÓu diÔn c¸c phÇn tö trong mét hµng, trôc x sÏ biÓu diÔn sè hµng.
VÝ dô: VÏ ®å thÞ biÓu thÞ sè sinh viªn tèt nghiªp cña mét tr−êng §¹i häc
tõ n¨m 1995 ®Õn 2001, biÕt sè sinh viªn tèt nghiÖp t−¬ng øng lµ 1000,
1200, 1800, 1850, 1750, 2100.
LËp ch−¬ng tr×nh vÏ nh− sau:
x=[1000, 1200, 1800, 1850, 1750, 2100]
bar(x);
title('SO LUONG SINH VIEN TOT NGHIEP HANG NAM')
xlabel('Nam')
ylabel('So luong sinh vien')
set(gca,'XTickLabel',{'1996';'1997';'1998';...
'1999';'2000';'2001'})
Ch¹y ch−¬ng tr×nh cho kÕt qu¶ lµ ®å thÞ d−íi ®©y:
S O L U O N G S IN H V IE N T O T N G H IE P H A N G N A M
2 500
2 000
So luong sinh vien
1 500
1 000
500
0
1996 199 7 1998 1999 2000 2001
N am
§å thÞ pie.
LÖnh Pie(x) biÓu thÞ thµnh phÇn phÇn tr¨m theo d÷ liÖu trong x. Mçi
phÇn tö trong x ®−îc ®¹i diÖn b»ng mét phÇn cña ®å thÞ Pie.
Pie(x,explode) ®Æt c¸c phÇn tö cho ®å thÞ Pie. Explode lµ mét vÐc t¬ hay
mét ma trËn cña sè 0 vµ 1 t−¬ng øng víi x. C¸c phÇn tö lµ 0 sÏ t−¬ng øng
víi c¸c phÇn t¹o thµnh mét khèi liÒn trong ®å thÞ pie. NÕu lµ gi¸ trÞ 1 th×
phÇn tö t−¬ng øng víi mÈu trªn ®å thÞ sÏ ®−îc t¸ch rêi khái khèi liÒn
trong ®å thÞ Pie. Explode ph¶i cã cì gièng víi x.
VÝ dô : BiÓu diÔn thµnh phÇn phÇn tr¨m cña c¸c lo¹i vËt liÖu cã
trong mét hçn hîp.
x=[7 15 56 12 10];

36. eplode= [1 0 0 0 0];
pie(x,eplode)
colormap jet
Ta ®−îc ®å thÞ :
7%
10%
15%
12%
56%
b. VÏ ®å thÞ 3D : dïng lÖnh surf, mesh, contour3
VÝ dô: VÏ ®å thÞ z=-20x2+x-15y2+5y , víi -4<x<4 vµ -4<y<4.
Viªt file p3d.m ®Ó vÏ ®å thÞ ( dïng lÖnh surf )nh− sau:
[x,y]=meshgrid(-4:.2:4,-4:.2:4);
z=-20*x.^2+x-15*y.^2+5*y;
surf(x,y,z)
title(' Do thi 3D')
xlabel(' truc x')
ylabel(' truc y')
zlabel(' truc z')
pause
KÕt qu¶ cho nh− h×nh d−íi ®©y:

37. Cßn hai ®å thÞ d−íi ®©y ®−îc vÏ b»ng lÖn mesh vµ lÖnh contour3:
- §å thÞ 3D dïng lÖnh mesh
- §å thÞ 3D dïng lÖnh contour

38. D o th i 3 D d u n g le n h c o n to u r
0
-1 0 0
-2 0 0
truc z
-3 0 0
-4 0 0
-5 0 0
40
30 40
20 30
20
10 10
tru c y tru c x

39. PhÇn 2
øng dông Matlab gi¶i mét sè bµi toÊn kÜ
thuËt
1. Bµi to¸n vÒ m¹ch ®iÖn
VÝ dô 1: TÝnh c−êng ®é dßng ®iÖn cña m¹ch ®iÖn cã c¸c trë kh¸ng phøc
d−íi ®©y, biÕt hiÖu ®iÖn thÕ nguån U=5V, c¸c trë kh¸ng: z1=1+0,5i,
z2=2+0,5i, z3=4+i, z4=z1 ( Ω ).
z1 z1 z1 z1
aaa
U=5v fff
z4 z4 z4 z4
Gi¶i:
ViÕt c¸c ph−¬ng tr×nh ®Þnh luËt KiÕc sèp cho m¹ch nh− sau:
(z1+z2+z4)I1- z2I2 = U
(z1+2z2+z4)I2 - z2I1- z2I3= 0
(z1+2z2+z4)I3- z2I2- z2I4= 0
(z1+z2+z3+z4)I4- z2I3 = 0
ViÕt l¹i hÖ ph−¬ng tr×nh trªn d−íi d¹ng ma trËn nh− sau:
(z1+z2+z4) - z2 0 0 I1 = U
- z2 (z1+2z2+z4)I2 - z2 0 I2 = 0
0 - z2 (z1+2z2+z4) - z2 I3 = 0
0 0 - z2 (z1+z2+z3+z4) I4 = 0
hay Z.I = U
víi Z lµ ma tr©n trë kh¸ng, I lµ ma trËn cét dßng ®iÖn, cßn U lµ ma trËn
cét thÕ hiÖu.
NghiÖm I ®−îc tÝnh nh− sau:
I=Z-1.U
D−íi ®©y lµ file ml12.m ®Ó gi¶i ph−¬ng tr×nh ma trËn trªn

40. % File ml12.m
% Chuong trinh giai mach dien tro khang phuc
z1=1+.5i; z2=2+.5i; z3=4+i; z4=z1; % Cac tro
khang
U=5; % Hieu dien the
nguon
% Ma tran tro khang
Z=[z1+z2+z4 -z2 0 0;...
-z2 z1+2*z2+z4 -z2 0;...
0 -z2 z1+2*z2+z4 -z2;...
0 0 -z2
z1+z2+z3+z4 ];
F=[ V 0 0 0 ]'; % Ma tran cot ve phai
I=inv(Z)*F % Tinh dong dien
Ch¹y ch−¬ng tr×nh cho kÕt qu¶ d−íi ®©y:
I=
1.3008 - 0.5560i
0.4560 - 0.2504i
0.1530 - 0.1026i
0.0361 - 0.0274i
VÝ dô 2: TÝnh dßng ®iÖn cho m¹ch cã R, L vµ C nh− h×nh vÏ, cho
E=60v, R=50 Ω , L=1H,
C=10-4F, t¹i thêi ®iÓm ban ®Çu i1(0)=0, i2(0)=0.
i1 L
i3
E oi R C
ViÕt hÖ ph−¬ng tr×nh vi ph©n cho m¹ch nh− sau:
Ldi1/dt + Ri2 = E
RCdi2/dt+ i2 - i1 = 0
ChuyÓn vÕ, viÕt l¹i hÖ ph−¬ng tr×nh trªn nh− d−íi ®©y:
i1’ = - Ri2/L + E/L (1)

41. i2’ = i1/RC - i2 /RC
Dïng hµm ode45, lËp ch−¬ng tr×nh ®Ó x¸c ®Þnh i1, i2 b»ng c¸c file
ml13.m vµ ml13a.m d−íi ®©y:
% File ml13.m CHUONG TRINHF TINH MACH DIEN
% CO R-L-C
global E R L C
E=60; L=1; R=50;C=.005 % Nhap cac so lieu
i0=[0 0]'; % Dieu kien ban dau
t=5; % thoi gian
[t,i]=ode45('ml13a',t,i0);
subplot(211)
plot(t,i(:,1))
title('GIAI MACH DIEN CO R- L- C')
ylabel('D.dien trong mach chinh I1 - A')
grid
subplot(212)
plot(t,i(:,2))
ylabel('D.dien trong mach re I2 - A')
xlabel(' Thoi gian')
grid
% File ml13a.m
function ic=ml13a(t,i)
global E R L C
ic=zeros(2,1);
ic(1)=-R/L*i(2)+E/L;
ic(2)=i(1)/(R*C)-i(2)/(R*C);
Ch¹y ch−¬ng tr×nh cho kÕt qu¶ lµ trÞ sè c−êng ®é dßng ®iÖn trong m¹ch
chÝhh i1 vµ m¹ch rÏ i2 nh− h×nh d−íi ®©y:

42. G IA I M A C H D IE N C O R - L - C
D.dien trong m ac h c hinh I1- A
1.5
1
0.5
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
1.5
D.dien trong m ach re I2 - A
1
0.5
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Th o i g ia n
§Ó kiÓm tra kÕt qu¶ trªn, ta so s¸nh nã víi kÕt qu¶ chÝnh x¸c cña hÖ
ph−¬ng tr×nh vi ph©n (1) lµ:
i1= 6/5- 6e-100t/5- 60te-100t
i2= 6/5- 6e-100t/5- 120te-100t
§å thÞ chÝnh x¸c cña i1 vµ i2 cã d¹ng nh− h×nh d−íi ®©y:
D o n g d ie n I1 = 6 / 5 - 6 / 5 e ( - 1 0 0 t ) - 6 0 t e ( - 1 0 0 t )
1 . 4
1 . 2
1
0 . 8
0 . 6
0 . 4
0 . 2
0
0 0 . 5 1 1 . 5 2 2 . 5 3 3 . 5 4 4 . 5 5
D o n g d ie n I2 = 6 / 5 - 6 / 5 e ( - 1 0 0 t ) - 1 2 0 t e ( - 1 0 0 t )
1 . 4
1 . 2
1
0 . 8
0 . 6
0 . 4
0 . 2
0
0 0 . 5 1 1 . 5 2 2 . 5 3 3 . 5 4 4 . 5 5
Ta thÊy kÕt qu¶ cña hai c¸ch tÝnh lµ nh− nhau.

43. §Ó thÊy sù dao ®éng cña m¹ch ®iÖn mét c¸ch râ nÐt ta t¨ng ®iÖn dung
cña tô ®iªn: lÊy C=0,005F råi ch¹y l¹i ch−¬ng tr×nh ta ®−îc kÕt qu¶ nh−
h×nh d−íi ®©y:
G IA I M A C H D IE N C O R - L - C
Dong dien trong m ach c hinh - A
6
4
2
0
-2
0 0 .5 1 1.5 2 2.5 3 3.5 4 4.5 5
Dong dien trong m ac h re R - A
2
1 .5
1
0 .5
0
0 0 .5 1 1.5 2 2.5 3 3.5 4 4.5 5
T h o i g ia n
2. Gi¶i bµi to¸n ®éng häc c¬ cÊu ph¼ng
VÝ dô : Gi¶i bµi to¸n ®éng häc c¬ cÊu cu lit
H·y x¸c ®Þnh chuyÓn vÞ, vËn tèc gãc, gia tèc gãc cña thanh cu lit 3 cña
c¬ cÊu cu lit, biÕt tr−íc kÝch th−íc c¸c kh©u: l0=0,5m, l1=0,2m, tay quay
1 quay ®Òu víi w1=8rad/s.
l1
ϕ1
l0 l3
ϕ3

44. Ta cã quan hÖ vÐc t¬ sau:
l 3 = l0 + l1
ViÕt l0 , l1 d−íi d¹ng sè phøc ta ®−îc:
l3 = l0ei π / 2 + l1ei ϕ 1 (1)
Dïng hµm abs ta tÝnh ®−îc trÞ sè cña vÐc t¬ l3 , dïng hµm angle ®Ó tÝnh
gãc chØ ph−¬ng cña vÐc t¬ nµy còng lµ gãc ϕ 3 cña cu lit.
l3a = abs( l3 ) (2)
ϕ 3 = angle( l3 ) (3)
§Ó tÝnh ®−îc vËn tèc gãc vµ gia tèc gãc cña cu lÝt ta thay l3 = l3aei ϕ 3
vµo (1) råi ®¹o hµm theo t, ta ®−îc:
l3aei ϕ 3 = l0ei π / 2 + l1ei ϕ 1
l3a’e i ϕ 3 + i ω 3 l3aei ϕ 3 = i ω 1 l1ei ϕ 1
Chia c¶ hai vÕ cho ei ϕ 3 :
l3a’ + i ω 3 l3a = i ω 1 l1ei (ϕ1 − ϕ 3 )
T¸ch phÇn thùc vµ ¶o, ta rót ra:
l3a’ = - ω 1 l1sin( (ϕ1 − ϕ 3 ) (4)
ω 3 = ω 1 l1cos (ϕ 1 − ϕ 3 ) / l3a (5)
§Ó cã gia tèc gãc, ta ®¹o hµm (5) :
α 3 = ( - ω 1 l1sin (ϕ 1 − ϕ 3 ) ( ω 1 - ω 3 ) l3a - l3a’ ω 3 )/ l3a (6)
C¨n cø vµo c¸c biÓu thøc (1), (2), (3), (4), (5) vµ (6) lËp ch−¬ng tr×nh tÝnh
c¸c chuyÓn vÞ vËn tèc vµ gia tèc nh− ®−îc viÕt trong file cl3.m d−íi ®©y.
KÕt qu¶ vÒ chuyÓn vÞ, vËn tèc vµ gia tèc gãc cu lÝt ®−îc cho d−íi d¹ng ®å
thÞ ë phÝa d−íi ch−¬ng tr×nh.
% CHUONG TRINH TINH CHUYEN DONG CUA CO CAU CU LIT
l1=.2; l0=.5; % Kich thuoc tay quay va
gia
w1=8; % Van toc goc khau dan -
rad/s
n=51; % So vi tri tay quay
df=2*pi/n;
f1=0:df:2*pi;
f1d=f1*180/pi; % Goc tay quay – do
l3=l0*exp(i*pi/2)+l1*exp(j*f1);
f3=angle(l3);
l3a=abs(l3);
l3ac=-l1*w1*sin(f1-f3);
w3=l1*w1*cos(f1-f3)./l3a;
alpha3=-(v32.*w3+l1*w1*(w3-w1).*sin(f3-
f1))./l3a;

45. subplot(311)
plot(f1d,f3*180/pi)
title(' CHUYEN DONG CUA CU LIT ')
ylabel(' C.vi goc Culit - do')
grid
subplot(312)
plot(f1d,w3)
ylabel(' Van toc goc Culit - rad/s')
grid
subplot(313)
plot(f1d,alpha3)
ylabel(' Gia toc goc Culit - rad/s^2')
xlabel(' Goc tay quay')
grid
CHUYEN DONG CUA CU LIT
120
Gia toc goc Culit - rad/s 2 toc goc Culit - rad/s C.vi goc Culit - do
100
80
60
0 50 100 150 200 250 300 350 400
5
0
-5
-10
V an
0 50 100 150 200 250 300 350 400
50
0
-50
0 50 100 150 200 250 300 350 400
Goc tay quay
3. Gi¶i bµi to¸n c©n b»ng m¸y

46. VÝ dô 1 : Gi¶i bµi to¸n c©n b»ng tÜnh
Cã trôc quay trªn cã g¾n c¸c khèi l−îng lÖch t©m ®Æt trong cïng mét mÆt
ph¼ng nh− h×nh vÏ. Trôc hiÖn ®ang mÊt c©n b»ng tÜnh.Ta tiÕn hµnh c©n
b»ng trôc quay b»ng ph−¬ng ph¸p sè phøc nh− sau:
Tõ ®iÒu kiÖn c©n b»ng tÜnh ta cã: m4
m1
m1r1 + m2r2 + m3r3 + m4r4 + mcbrcb = 0 r1
r4
r2
mcb rcb
r3
BiÓu diÔn c¸c vÐc t¬ d−íi d¹ng sè phøc ta ®−îc:
mcbrcb = - (m1r1ei ϕ 1 + m2r2ei ϕ 2 + m3r3ei ϕ 3 + m4r4ei ϕ 4 )
Tõ ®ã tÝnh ®−îc trÞ sè cña tÝch mcbrcb vµ gãc chØ ph−¬ng ϕ cña b¸n kÝnh
vÐc t¬ rcb b»ng c¸ch dïng hµm abs vµ hµm angle.
mcbrcb = abs( mcbrcb);
ϕ = angle(mcbrcb )
Ch−¬ng tr×nh tÝnh nh− sau:
% File canbt.m
% TINH CAN BANG TINH
m1=12; m2=15; m3=27;m4=30; % Cac khoi
luong
r1=.6; r2=.8; r3=.5; r4=.4; % Tri so cac ban
kinh vec to
f1=pi/2; f2=pi/12; % Cac goc chi
phuong
f3=-pi/6;f4=2*pi/3; % cua ban kinh ri
mrcb=-m1*r1*exp(i*f1)-m2*r2*exp(i*f2)-
m3*r1*exp(i*f3)-...
m4*r4*exp(i*f4);
mr=abs(mrcb) % Tri so mcg*rcb
f=angle(mrcb)*180/pi % Goc chi phuong cua
ban
% kinh vecto rcb (do)
Ch¹y ch−¬ng tr×nh trªn kÕt qu¶ nhËn ®−îc lµ tÝch mcbrcb ( kÝ hiÖu
lµ mr) vµ gãc chØ ph−¬ng (kÝ hiÖu lµ f) cña b¸n kÝnh vÐc t¬ cña khèi
l−îng c©n b»ng (tÝnh ra ®é):
mr =
23.3171

47. f=
-147.2962
NÕu chän tr−íc r = rcb= 0,6m th× khèi l−îng c©n b»ng cÇn ®Æt vµo lµ:
m = mcb = mr/rcb =38,86 kg.
VÝ dô 2: Gi¶i bµi to¸n c©n b»ng ®éng vËt quay
Bµi to¸n: H·y c©n b»ng ®éng trôc quay cã g¾n c¸c khèi l−îng ®Æt lÖch
t©m trªn nh÷ng mÆt ph¼ng kh¸c nhau nh− h×nh vÏ d−íi ®©y. BiÕt hai mÆt
ph¼ng T vµ P lµ hai mÆt ph¼ng c©n b»ng.
m1 T m1
P
m2 m2 r1
r1 r2 r2 m4
r4 A B
m4 rP mP l2
mP l1
r3 l4
r3
m3 l3
m3
rT
mT mT l
C¸c khèi l−îng, ®é dµi c¸c b¸n kÝnh vÐc t¬ t−¬ng øng vµ c¸c kÝch th−íc
kh¸c ®−îc cho nh− sau: m1=20 kg, m2=15 kg, m3=17 kg, m4=26 kg,
r1=0,6m, r2= 0,3m, r3=0,4m, r4=0,4m, l1=0,3m, l2=0,5m, l3=0,8m,
l4=1,2m, l=1,5m . C¸c b¸n kÝnh vÐc t¬ r1, r4 t−¬ng øng cã ph−¬ng th¼ng
®øng vµ n»m ngang, cßn vÐc t¬ r2, r3 lµm víi ph−¬ng ngang gãc
ϕ 2 = 30 0 vµ ϕ 3 = −60 0 .
Ta gi¶i nh− sau: Gi¶ sö hai ®èi träng khèi l−îng mT vµ mP ®· ®−îc ®Æt
vµo hai mÆt ph¼ng c©n b»ng T vµ P, c¸c b¸n kÝnh vÐc t¬ t−¬ng øng lµ rT
vµ rP , vµ hiÖn giê trôc ®· ®−îc c©n b»ng tÜnh vµ ®éng. Tõ ph−¬ng tr×nh
c©n b»ng m« men ®èi víi ®iÓm A cña c¸c lùc qu¸n tÝnh vµ ph−¬ng tr×nh
tæng vÐc t¬ c¸c lùc qu¸n tÝnh b»ng 0 ta cã hai ph−¬ng tr×nh vÐc t¬ sau:
m1l1r1 + m2l2r2 + m3l3r3 + m4l4r4 + mPlrP =0 (1)
m1r1 + m2r2 + m3r3 + m4r4 + mPrP +mTrT=0 (2)
Ta gi¶i (1) tr−íc ®Ó x¸c ®Þnh mP, rP , sau ®ã gi¶i tiÕp (2) ®Ó x¸c ®Þnh nèt
mT , rT .
V× : r1 = r1 eiϕ , r2 = r2 eiϕ , r3 = r3 eiϕ , r4 = r4 eiϕ
1 2 3ta viÕt l¹i (1) d−íi
4
d¹ng sè phøc nh− sau:

48. mPlrP = mPlrP eiϕ = - m1l1r1 eiϕ - m2l2r2 eiϕ - m3l3r3 eiϕ - m4l4r4 eiϕ
P 1 2 3 4
hay : mPrP = (- m1l1r1 eiϕ - m2l2r2 eiϕ - m3l3r3 eiϕ - m4l4r4 eiϕ ) / l
1 2 3 4
TrÞ sè cña tÝch mPrP ®−îc tÝnh nh− sau:
mP rP = abs(mPrP )
Chän tr−íc rP ta sÏ x¸c ®Þnh ®−îc khèi l−îng cña ®èi träng cÇn ®Æt trªn
mÆt ph¼ng c©n b»ng ph¶i P: mP= mP rP /rP
Gãc chØ ph−¬ng cña b¸n kÝnh vÐc t¬ :
ϕ P = angle( mPrP )
Sau khi ®· cã mP ,rP ta gi¶i (2) ®Ó x¸c ®Þnh mTrT:
mTrT = - ( m1r1 + m2r2 + m3r3 + m4r4 + mPrP )
TrÞ sè cña mTrT ®−îc tÝnh theo:
mTrT = abs( mTrT )
NÕu chän tr−íc mT ta sÏ x¸c ®Þnh ®−îc ®é dµi cña b¸n kÝnh vÐc t¬ rT :
rT = m TrT / mT
Gãc chØ ph−¬ng cña b¸n kÝnh vÐc t¬ rT
ϕ T = angle(mTrT)
§Õn ®©y bµi to¸n ®· gi¶i xong.
D−íi ®©y lµ ch−¬ng tr×nh tÝnh:
% File canbd.m
% CHUONG TRINH TINH CAN BANG DONG CHO VAT QUAY
m1=20; m2=15; m3=17; m4=26; % Khoi luong cac
% vat lech tam - kg
r1a=0.6; r2a= 0.3; r3a=0.4; r4a=0.4; % Do dai cac ban
% kinh vec
to -m
l1=0.3; l2=0.5; l3=0.8; l4=1.2; % Khoang cach doc
% truc den mat phang
T
% cua cacs khoi
luong
l=1.5; % Khoang cach giua hai mat phang
c.bang
f1=pi/2; f2=pi/6; % Cac goc chi phuong cua cac
f3=-pi/3; f4=pi; % ban kinh vec to -m
r1=r1a*exp(i*f1); % Cac ban kinh vec to
r2=r2a*exp(i*f2); % duoi dang so phuc
r3=r3a*exp(i*f3);
r4=r4a*exp(i*f4);
mPrP=(-m1*l1*r1-m2*l2*r2-m3*l3*r3-m4*l4*r4)/l; % Vec to
mPrPa=abs(mPrP); % Tri so cua tich mPrP -
kg.m
rPa=0.5; % Chon truoc tri so v.to rP

49. mP=mPrPa/rPa; % Khoi luong doi trong mP
fP=angle(mPrP)*180/pi; % Goc chi phuong cua rP
rP=mPrP/mP; % ban kinh vec to cua doi trong mP
mTrT=-m1*r1-m2*r2-m3*r3-m4*r4-mP*rP;
mTrTa=abs(mTrT); % Tri so tich mTrT
mT=10; % chon truoc doi trong trai
mT - kg
rTa=mTrTa/mT; % Do dai ban kinh vec to rT
fT=angle(mTrT)*180/pi; % Goc chi phuong cua vec to rT -
do
disp(' DOI TRONG DAT LEN M.PHANG P ')
disp(' mP(kg) rP(m) fP(do)')
P=[ mP rPa fP];
disp(P)
disp(' DOI TRONG DAT LEN M.PHANG T ')
disp( ' mT (kg) rT(m) fT (do)')
T=[ mT rTa fT];
disp(T)
Ch¹y ch−¬ng tr×nh víi trÞ sè b¸n kÝnh vÐc t¬ cña ®èi träng ®Æt trªn mÆt
ph¼ng c©n b»ng ph¶i rP vµ khèi l−îng ®èi träng ®Æt trªn mÆt ph¼ng c©n
b»ng tr¸i mT ®−îc chän tr−íc:
rP = 0,5 m vµ mT = 10 kg
ta ®−îc kÕt qu¶ lµ c¸c khèi l−îng cña c¸c ®èi träng ( tÝnh b»ng kg), ®é
dµi c¸c b¸n kÝnh vÐc t¬ (tÝnh b»ng m)vµ c¸c gãc chØ ph−¬ng t−¬ng øng
cña chóng (tÝnh b»ng ®é) nh− ®−îc biÓu diÔn d−íi ®©y:
DOI TRONG DAT LEN M.PHANG P
mP(kg) rP(m) fP(do)
10.4153 0.5000 -0.1014
DOI TRONG DAT LEN M.PHANG T
mT (kg) rT(m) fT (do)
10.0 0.8613 -104.1446
VÞ trÝ cña c¸c ®èi träng ®−îc thÓ hiªn trªn h×nh vÏ.
4. TÝnh thiÕt kÕ bé truyÒn b¸nh r¨ng
VÝ dô: TÝnh kho¶ng c¸ch trôc cña bé truyÒn b¸nh r¨ng trô r¨ng th¼ng A
vµ kh¶o s¸t sù phô thuéc gi÷a A vµ tØ sè truyÒn i khi c¸c th«ng sè kh¸c lµ
kh«ng ®æi
Kho¶ng c¸ch trôc cña bé truyÒn b¸nh r¨ng trô r¨ng th¼ng ®−îc tÝnh theo
c«ng thøc cã d¹ng quen thuéc sau:

50. 2
⎛ 1,05.10 6 ⎞ KN
3
⎜ [σ ] i ⎟ ϕ n
A ≥ (i + 1) ⎜ ⎟
⎝ tx ⎠ A 2
Cho øng suÊt tiÕp xóc cho phÐp [σ ]tx = 546N / mm 2 , hÖ sè t¶i träng K=1,3,
hÖ sè chiÒu réng b¸nh r¨ng ϕ A = 0,4 , tèc ®é vßng quay trôc bÞ dÉn n2 = 60
v/ph, c«ng suÊt truyÒn N=5 kw. §Ó thÊy ®−îc quan hÖ gi÷a trÞ sè
kho¶ng c¸ch trôc vµ tØ sè truyÒn ta cho tØ sè truyÒn i biÕn thiªn tõ 1 ®Õn
10, sau ®ã tÝnh c¸c trÞ sè A t−¬ng øng. C¸ch tÝnh ®−îc tr×nh bµy trong file
kctA.m vµ ®å thÞ trªn h×nh d−íi ®©y m« t¶ quan hÖ gi÷a A vµ i lµ kÕt qu¶
thu ®−îc khi ch¹y ch−¬ng tr×nh.
Ta thÊy mét ®iÒu thó vÞ lµ kho¶ng c¸ch trôc cã trÞ sè nhá nhÊt khi tØ sè
truyÒn b»ng 2 vµ kho¶ng c¸ch trôc t¨ng nhanh khi tØ sè truyÒn v−ît qu¸
4.
T IN H K H . C A C H T R U C B O T R U Y E N B . R A N G
240
230
220
K h. cach truc - mm
210
200
190
180
1 2 3 4 5 6 7 8 9 10
T i s o tr u y e n
% File kctA.m
% TINH KHOANG CACH TRUC BO TRUYEN BANH RANG
i=1:.5:10; % Ti so truyen
ustx = input(' ung suat tiep xuc - N/mm^2
ustx=')
k = input('he so tai trong la k=')
phiA = input('he so chieu rong banh rang
phiA=')
teta=input('he so tang kha nang tai teta=')
n2= input('so vong quay banh rang n2=')
N=input('cong suat la - KW N=')
A
=(i+1).*((1.05*10^6./(ustx*i)).^2*k*N/(phiA*teta*n2)).^(1
/3);

51. plot(i,A)
title(' TINH KH. CACH TRUC BO TRUYEN B.RANG')
xlabel('Ti so truyen')
ylabel(' Kh. cach truc - mm')
grid
5. TÝnh søc bÒn trôc
Trong tÝnh søc bÒn trôc trong c¸c hép gi¶m tèc viÖc x¸c ®Þnh c¸c ph¶n
lùc t¹i c¸c gèi vµ trÞ sè m« men uèn t¹i c¸c tiÕt diÖn nguy hiÓm ( th−êng
lµ bµi to¸n kh«ng gian) cã thÓ ®−îc thùc hiÖn nhê lËp mét ch−¬ng tr×nh
tÝnh nh− trong vÝ dô d−íi ®©y:
y
PAy PBy
0 A B
C x
z lA PAz PBz
lB
lC
Gi¶ sö trôc chÞu t¸c dông cña hÖ lùc nh− h×nh vÏ. Gäi R0y,R0z,RAy,Raz lµ
c¸c thµnh phÇn ph¶n lùc tõ c¸c æ t¹i 0 vµ C. Theo ®iÒu kiÖn c©n b»ng vÒ
m« men ®èi víi ®iÓm O vµ c©n b»ng tæng vÐc t¬ lùc , ta viÕt ®−îc hai
ph−¬ng tr×nh c©n b»ng sau:
lAxPAy+lAxPAz+ lBxPBy+lBxPBz+ lCxRCy+lCxRCz = 0
(1)
PAy+PAz+ PBy+PBz+ RCy+RCz+ R0y+R0z = 0
(2)
Thay Rc=RCy+RCz , R0= R0y+R0z vµo (1) vµ (2) ta rót ra:
lCxRC = - ( lAxPAy+lAxPAz+ lBxPBy+lBxPBz )
(3)
R0 = - ( PAy+PAz+ PBy+PBz+ RCy+RCz )
(4)
Sau khi tÝnh ®−îc c¸c ¸p lùc khíp ®éng t¹i C vµ O, ta cã thÓ tÝnh ®−îc
m« men uèn t¹i c¸c tiÕt diÖn nguy hiÓm lµ A vµ B dùa vµo c¸c ph−¬ng
tr×nh c©n b»ng sau:
MB + lBC x RC = 0
(5)
MA+(-lA x R0) = 0
(6)

52. §Ó gi¶i c¸c ph−¬ng tr×nh vÐc t¬ (3), (4), (5) vµ (6) ta ®−a ra c¸c vÐc t¬
®¬n vÞ cña hÖ toa ®é §Ò c¸c lµ i, j vµ k vµ dïng hµm cross(...,...) ®Ó nh©n
cã h−íng hai vÐc t¬. C¸ch lµm ®−îc thÓ hiÖn râ trong file plkd.m d−íi
®©y:
% File plkd.m
% Tinh phan luc tai khop dong va mo men uon
% Cac Vec to don vi cua he toa do De cac
I=[1 0 0]';
J=[0 1 0]';
K=[0 0 1]';
% Vec to vi tri
la=100; lb=250; lc=350; lbc=100;
La=100*I; Lb=250*I; Lc=350*I; Lbc=lbc*I;
% Luc tac dung
Pay=-1.4*J; Paz=.5*K;
Pby=-.9*J; Pbz=1.4*K;
% Tinh phan luc goi C
LcRc=-cross(La,Pay)-cross(La,Paz)-cross(Lb,Pby)-
cross(Lb,Pbz);
Rc0=LcRc/lc; % Vec to phan luc tai
goi C(chua quay)
Q=[0 0 0; 0 0 -1; 0 1 0]; % Ma tran chuyen
(quay)
Rc=-Q*Rc0 % Vec to phan luc tai
goi C
% Tinh phan luc tai goi O
R0=-(Pay+Paz+Pby+Pbz+Rc)
% Tinh mo men uon tai tiet dien B va A
Mb=-cross(Lbc,Rc)
Ma=-cross(-La,R0)
% ---------------------------------------------
Ch¹y ch−¬ng tr×nh plkd.m trªn mµn h×nh Command Window, kÕt qu¶
cña c¸c ph¶n lùc khíp ®éng t¹i O , C vµ c¸c m« men uèn t¹i mÆt c¾t A vµ
B nhËn ®−îc nh− sau:
Rc =

53. 0
1.0429
-1.1429
R0 =
0
1.2571
-0.7571
Mb =
0
-114.2857
-104.2857
Ma =
0
-75.7143
-125.7143
» plkd
Rc =
0
1.0429
-1.1429
R0 =
0
1.2571
-0.7571
Mb =
0
-114.2857
-104.2857
Ma =
0
75.7143
125.7143
6. TÝnh dao ®éng
a. TÝnh dao ®éng cña hÖ mét bËc tù do

54. Gi¶ sö cã hÖ dao ®éng mét bËc tù do nh− h×nh vÏ: m kµ khèi l−îng cña
vËt, c lµ ®é cøng lß xo (N/m), k lµ hÖ sè c¶n cña gi¶m chÊn thuû lùc
(Ns/m), cßn F lµ lùc kich thÝch víi F=F0coswt ( F0 lµ biªn ®é cña lùc –
N, w lµ tÇn sè gãc – rad/s).
ViÕt ph−¬ng tr×nh ®Þnh luËt 2 cho vËt ;
mx’’= -kx’-cx +F0coswt (1)
trong ®ã x, x’, x’’ lÇn l−ît lµ chuyÓn vÞ, x
vËn tèc vµ gia tèc cña vËt. k F
ta biÕn ®æi (1) nh− sau:
c m
x’’= -kx’/m - cx/m + +F0coswt/m (2)
§Æt x1=x’, x2= x th× x1’= x’’, x2’= x1, ph−¬ng tr×nh vi ph©n cÊp 2 trªn sÏ
®−îc viÕt thµnh hÖ hai ph−¬ng tr×nh bËc nhÊt víi hai Èn lµ x1 vµ x2 nh−
d−íi ®©y:
x1’= - kx1/m - cx2m + F0coswt/m (3)
x2’= x1
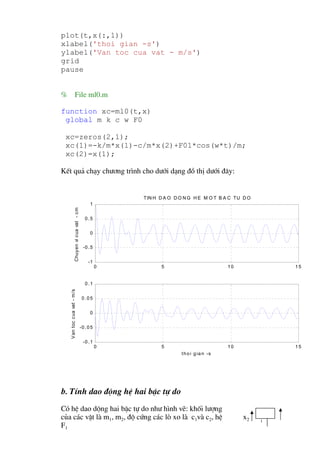
Ch−¬ng tr×nh ®Ó gi¶i hÖ (3) ®−îc viÕt trong c¸c file ml00.m vµ ml0.m
nh− d−íi ®©y:
% File ml00.m
% Chuongtrinh tinh dao dong he 1 bac tu do co
giam chan
% thuy luc chui luc kich dong dang F=F0cos(wt)
global m k c w F0
m=100; % Khoi luong vat - kg
c=10000; % Do cung lo xo - N/m
k=80; % He so can nhot Ns/m
w1=sqrt(c/m) % Tan so dao dong rieng
w=6; % Tan so luc kich dong
tc=15; % Thoi gian dao dong
x0=[0 .01 ]' ; % Dieu kien ban dau (van
toc, toa do)
F0=20 ; % Bien do luc kich dong - N
[t,x]=ode45('ml0',tc,x0);
subplot(211)
plot(t,x(:,2))
title(' TINH DAO DONG HE MOT BAC TU DO')
ylabel('Chuyen vi cua vat - cm')
grid
subplot(212)

55. plot(t,x(:,1))
xlabel('thoi gian -s')
ylabel('Van toc cua vat - m/s')
grid
pause
% File ml0.m
function xc=ml0(t,x)
global m k c w F0
xc=zeros(2,1);
xc(1)=-k/m*x(1)-c/m*x(2)+F01*cos(w*t)/m;
xc(2)=x(1);
KÕt qu¶ ch¹y ch−¬ng tr×nh cho d−íi d¹ng ®å thÞ d−íi ®©y:
TIN H D A O D O N G H E M O T B A C TU D O
1
Chuyen vi c ua vat - c m
0.5
0
-0 . 5
-1
0 5 10 15
0.1
V an toc c ua vat - m /s
0.05
0
-0 . 0 5
-0 . 1
0 5 10 15
t h o i g ia n -s
b. TÝnh dao ®éng hÖ hai bËc tù do
Cã hÖ dao déng hai bËc tù do nh− h×nh vÏ: khèi l−îng
cña c¸c vËt lµ m1, m2, ®é cøng c¸c lß xo lµ c1vµ c2, hÖ x2
F1

56. sè c¶n nhít lµ k1 vµ k2, lùc kÝch thich ®Æt lªn hÖ lµ c2 k2
F1=F10sinw1t, F2=F20sinw2t.
x1
F2
c1
k1
ViÕt hÖ ph−¬ng tr×nh ®Þnh luËt 2 Niu t¬n cho
tõng vËt:
m1x1’’=- k1x1’- c1x1+k2(x2’-x1’)+c2(x2-x1) +F01sinw1t
m2x2’’= - k2 (x2’-x1’)- c2(x2 -x1)+F02sinw2t
x1’’ = - (k1+k2)x1’/m1- (c1+c2)x1/ m1+k2x2’/ m1+c2x2 / m1+ F01sinw1t/ m1
(1)
x2’’ = k2x1’/ m2 + c2x1 / m2 - k2x2’ / m2 - c2x2/ m2 + F02sinw2t/ m2
T−¬ng tù nh− khi gi¶i ph−¬ng tr×nh vi ph©n c©p hai ë phÇn trªn, ta còng
®Æt:
y1 = x1’, y2 = x1, y3 = x2’, y4 = x2.
(2)
Rót ra:
y1’=x1’’
(3)
y2’=y1
y3’= x2’’
y4’=y3
Thay (1) vµo (3) vµ chó ý ®Õn (2) ta lËp ®−îc hÖ gåm bèn ph−¬ng tr×nh
vi ph©n tuyÕn tÝnh bËc nhÊt. HÖ ph−¬ng tr×nh nµy vµ c¸ch gi¶i nã ®−îc
cho trong file ml11.m vµ ml1.m ë d−íi ®©y.
Nh©n tiÖn ®©y ta còng thö t¸c dông cña gi¶m chÊn ®éng lùc: theo lÝ
thuyÕt, nÕu lùc kÝch thÝch vµo vËt 2 b»ng 0 ( F2=0), vµ c¸c th«ng sè cña
bé gi¶m chÊn ®éng lùc gåm khèi l−îng m2 vµ lß xo cã ®é cøng c2 tho·
m·n ®iÒu kiÖn: c2/m2 = w12 ( w1 lµ tÇn sè lùc kÝch thÝch cña lùc F1 lªn vËt
1) th× dao ®éng cña vËt chÝnh 1 cã khèi l−îng m1 ®ã sÏ b»ng 0. Trong
ch−¬ng tr×nh ta cho F20=0, m2=10 kg, c2=510 N/m vµ w1= c 2 / m 2 .
% File ml11.m
% Tinh dao dong he hai bac tu do
global m1 m2 k1 k2 c1 c2 w F10 F20
m1=100; % Khoi luong vat thu nhat - kg
c1=10000; % Do cung lo xo thu nhat - N/m
m2=10; % Khoi luong vat thu 2 - kg
c2=510; % Do cung lo xo thu 2 - N/m
k1=220; k2=0; % He so can nhot cua giam chan
- Ns/m
w20=sqrt(c2/m2)

57. x0=[0 .0 0 .0]'; % Dieu kien ban dau
F10=100; % Bien do luc tac dung vao
vat 1 – N
F20=0; % -- 2
w1=w20; % Tan so goc cua luc k.thich
- rad/s
[t,y]=ode45('ml1',tc,x0);
subplot(211)
plot(t,y(:,2)*100)
title('TINH DAO DONG HE HAI BAC TU DO')
ylabel('Chuyen vi cua vat 1 - cm')
grid
subplot(212)
plot(t,y(:,4)*100)
xlabel(' Thoi gian - s')
ylabel('Chuyen vi cua vat 2 - cm')
grid
pause
% File ml1.m
% Chuong trinh con tinh dao dong he hai bac tu
do
function yc=ml1(t,y)
global m1 m2 k1 k2 c1 c2 w F10 F20
yc=zeros(4,1);
yc(1)=-(k1+k2)/m1*y(1)-(c1+c2)/m1*y(2)+...
k2/m1*y(3)+c2/m1*y(4)+F10*sin(w1*t)/m1;
yc(2)= y(1);
yc(3)= k2/m2*y(1)+c2/m2*y(2)-k2/m2*y(3)-
c2/m2*y(4)+...
F20*sin(w2*t)/m2;
yc(4)= y(3);
Ch¹y ch−¬ng tr×nh sÏ cho kÕt qu¶ d−íi d¹ng ®å thÞ sau:

58. T IN H D A O D O N G H E H A I B A C TU D O
2
Chuy en vi c ua vat 1 - cm
1
0
-1
-2
0 2 4 6 8 10 12 14 16 18 20
40
Chuy en vi c ua vat 2 - c m
20
0
-2 0
-4 0
0 2 4 6 8 10 12 14 16 18 20
Th o i g ia n - s
Ta thÊy mét ®iÒu thó vÞ lµ : ®óng nh− dù ®o¸n, biªn ®é dao ®éng cña vËt
chÝnh 1 gi¶m dÇn theo thêi gian vµ sÏ t¾t h¼n sau Ýt gi©y n÷a.
c. X¸c ®Þnh tÇn sè dao ®éng riªng cña hÖ nhiÒu bËc tù do
Víi hÖ c¬ häc nhiÒu bËc tù do viÖc x¸c ®Þnh c¸c tÇn sè dao ®éng riªng
cña hÖ cã mét ý nghÜa quan träng. Matlab gióp ta gi¶i bµi to¸n nµy kh«ng
mÊy khã kh¨n.
VÝ dô: Cã hÖ gåm bèn toa xe mãc nèi víi nhau, h·y x¸c ®Þnh tÇn sè dao
®éng riªng cña hÖ theo chiÒu däc. BiÕt khèi l−îng c¸c toa xe lµ m1=45T,
m2=35T, m3=40T, m4=50T, ®é cøng c¸c lß xo lµ c1=c2=800KNm,
c3=1000KN/m.
m1 x1 m2 x2 m3 x3 m4 x4
§Ó gi¶i bµi to¸n tr−íc hÕt ta ph¶i lËp c¸c ma trËn khèi l−îng vµ ma tr©n
®é cøng nh− sau:
- Ma trËn khèi l−îng:
M=diag(m1, m2, m3, m4); ( Ma trËn chÐo cã c¸c phÇn tö lµ c¸c
khèi l−îng)
-Ma trËn ®é cøng:

59. c1 -c1 0 0
C= -c1 c1+c2 -c2 0
0 -c2 c2+c3 -c3
0 0 -c3 c3
- Dïng hµm eig ®Ó x¸c ®Þnh c¸c trÞ riªng vµ vÐc t¬ riªng:
[ X, L] = eig( C, M);
trong ®ã L lµ ma trËn ®−êng chÐo mµ mçi phÇn tö trªn ®−êng chÐo lµ mét
trÞ riªng (eigenvalue) lµ w12, w22, w32 vµ w42 . Cßn w1 w2, w3 vµ w4 chÝnh lµ
c¸c tÇn sè dao ®éng riªng cña hÖ (rad/s).
Ma trËn (hµng) cña c¸c tÇn sè dao ®éng riªng ®−îc x¸c ®Þnh nh− sau:
w = diag(sqrt(L));
KÕt qu¶ tÝnh b»ng sè cô thÓ nhËn ®−îc nhê ch¹y ch−¬ng tr×nh trong file
tansd.m d−íi ®©y:
% File t¸nd.m
% CHUONG TRINH TINH TAN SO DAO DONG RIENG
% CUA HE NHIEU BAC TU DO
m1=45000; m2=35000;
m3=40000; m4=50000; % Khoi luong cac toa xe
c1=800000;c2=c1; % Do cung lo xo N/m.
c3=1000000;
% Ma tran khoi luong va ma tran do cung
m=[m1 m2 m3 m4];
M=diag(m);
C=[c1 -c1 0 0; -c1 c1+c2 -c2 0 ; 0 -c2 c2+c3
-c3;...
0 0 -c3 c3];
% Tinh tri rieng va vec to rieng
,L]=eig(C,M);
wb=diag(L); % Cac tri rieng
w=sqrt(wb) % Cac tan so dao dong rieng -
rad/s
C¸c gi¸ trÞ tÇn sè dao ®éng riªng ®−îc ch−¬ng tr×nh cho d−íi ®©y:
w=
8.6524
6.5472
0 + 0.0000i
3.2807

60. Ta thÊy cã mét tÇn sè dao ®éng riªng b»ng 0 : w3=0. §iÒu nµy vÒ mÆt lÝ
thuyÕt dao ®éng th× hoµn toµn hîp lÝ v× nã t−¬ng øng vèi mét d¹ng dao
®éng riªng cña hÖ trong ®ã toµn hÖ chuyÓn ®éng nh− mét vËt r¾n.
KÕt luËn
Qua hai phÇn nghiªn cøu t×m hiÓu phÇn mÒm lËp tr×nh Matlab vµ øng
dông nã ®Ó gi¶i mét sè bµi to¸n kÜ thuËt, chóng t«i thÊy r»ng ®©y lµ mét
phÇn mÒm rÊt m¹nh, dÔ sö dông vµ rÊt cã hiÖu qu¶ trong tÝnh to¸n, ®Æc
biÖt thÝch hîp cho viÖc nghiªn cøu trong lÜnh vùc khoa häc kÜ thuËt.
§ång thêi chóng t«i còng thÊy râ r»ng: ®Ó hiÓu cÆn kÏ còng nh− sö dông
®−îc hÕt kh¶ n¨ng cña Matlab th× ®ã còng kh«ng ph¶i lµ chuyÖn dÔ, v×
b¶n th©n nã lµ mét phÇn mÒm lín. Tuy nhiªn, trong ph¹m vi cña ®Ò tµi
nghiªn cøu nµy, nh÷ng vÊn ®Ò c¬ b¶n vµ nh÷ng øng dông phæ biÕn cña
phÇn mÒm ®· ®−îc tr×nh bµy vµ ®· cã nh÷ng vÝ dô minh ho¹ cô thÓ. Tõ
nh÷ng phÇn c¬ b¶n nµy, ng−êi ®äc qua sö dông thùc tÕ phÇn mÒm sÏ cã
kh¶ n¨ng tù t×m hiÓu s©u h¬n nhê tra cøu phÇn Help trong m¸y.
C¸ch tr×nh bµy chóng t«i ®· cè g¾ng sao cho ng¾n gän, dÔ hiÓu vµ thiªn
vÒ thùc hµnh. Mét trong nh÷ng môc ®Ých chÝnh cña nhãm nghiªn cøu lµ
biÕn kÕt qu¶ nghiªn cøu nµy thµnh tµi liÖu ®Ó t×m hiÓu vµ sö dông Matlab
cho nh÷ng ng−êi quan t©m, ®Æc biÖt lµ cho sinh viªn. Hi väng lµ víi tµi
liÖu nµy, ng−êi häc cã thÓ tù thùc hµnh trªn m¸y tÝnh ®Ó lËp c¸c ch−¬ng
tr×nh tÝnh to¸n cho bµi to¸n cña m×nh.
Do khu«n khæ thêi gian cã h¹n, cßn mét phÇn thø hai n÷a cña Matlab mµ
chóng t«i ch−a kÞp nghiªn cøu: ®ã lµ phÇn SIMULINK. §©y lµ phÇn
mÒm m« pháng rÊt m¹nh vµ hiÖu qu¶ cña Matlab, cho phÐp gi¶i®−îc
nhiÒu lo¹i bµi to¸n phøc t¹p. Chóng t«i hi väng sÏ cã ®iÒu kiÖn nghiªn
cøu tiÕp trong thêi gian tíi.