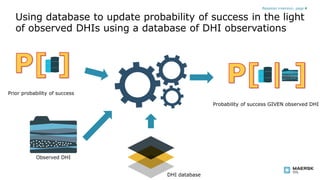
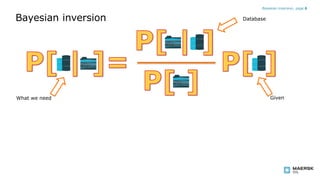
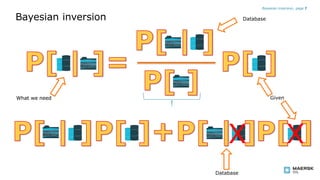
The document discusses using Bayesian updating to analyze SAAM data. It describes using a Bayesian inversion approach to calculate the probability of success given observed data. The key points are: - It formulates the approach using evidence ratios and probable probabilities rather than raw probabilities, which provides a simpler additive function of the prior probability. - It establishes probabilities of different data observations given success or failure by analyzing frequencies in a database of past observations. 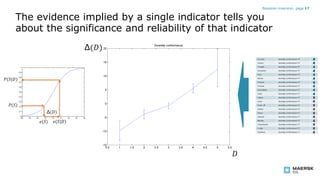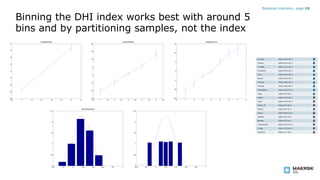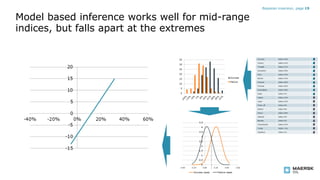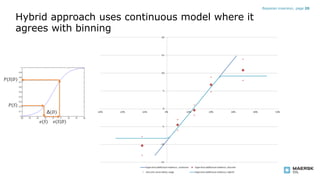- The evidence implied by a single data indicator provides information on how significant and reliable that indicator is. Binning data works best with around 5 bins partitioned by samples rather than a continuous index. A hybrid model combines continuous modeling with binning.

1. Bayesian updating using SAAM data
September 2016, SAAM Consortium Meeting
Graeme Keith, Maersk Oil

2. Overview
Fundamental approach – Bayesian inversion
Formulation – Evidence and probable probabilities
Results

3. Overview
Fundamental approach – Bayesian inversion
Formulation – Evidence and probable probabilities
Results

4. Using database to update probability of success in the light
of observed DHIs using a database of DHI observations
Bayesian inversion, page 4
Prior probability of success
Observed DHI
DHI database
Probability of success GIVEN observed DHI

5. Using database to update probability of success in the light
of observed DHIs using a database of DHI observations
Bayesian inversion,
page 5
Prior probability of success
Observed DHI
DHI database
Probability of success GIVEN observed DHI
Probability of observed DHI GIVEN success

6. Bayesian inversion
Bayesian inversion, page 6
What we need Given
Database

7. Bayesian inversion
Bayesian inversion, page 7
What we need
X X
What we need Given
Database
Database

8. What is the probability we see the observed DHI if
there is [not] oil in the ground
Bayesian inversion, page 8
Success
Victory
Triumph
Sensation
Glory
Riches
Fortune
Fortuity
Serendipity
Fluke
Failure
Loser
Write-off
Defeat
Fiasco
Debacle
Blunder
Catastrophe
Turnip
Washout
X
X
X
X
X
X
X
X
X
X
X

9. What is the probability we see the observed DHI if
there is [not] oil in the ground
Bayesian inversion, page 9
Success Flat spot=“4”
Victory Flat spot=“3”
Triumph Flat spot=“5”
Sensation Flat spot=“2”
Glory Flat spot=“4”
Riches Flat spot=“1”
Fortune Flat spot=“5”
Fortuity Flat spot=“3”
Serendipity Flat spot=“2”
Fluke Flat spot=“1”
Failure Flat spot=“4”
Loser Flat spot=“2”
Write-off Flat spot=“3”
Defeat Flat spot=“4”
Fiasco Flat spot=“2”
Debacle Flat spot=“1”
Blunder Flat spot=“3”
Catastrophe Flat spot=“2”
Turnip Flat spot=“3”
Washout Flat spot=“1”
X
X
X
X
X
X
X
X
X
X
X
Condition on single DHI score, say flat spot
𝑃(flat spot = "3"|𝑆) 𝑃(flat spot = "3"|𝐹)
Use the incidence of 3s amongst the success (failure
cases) to establish these probabilities

10. What is the probability we see the observed DHI if
there is [not] oil in the ground
Bayesian inversion, page 10
Success Index=14% bin 3
Victory Index=21% bin 4
Triumph Index=11% bin 3
Sensation Index=16% bin 4
Glory Index=12% bin 3
Riches Index=14% bin 3
Fortune Index=18% bin 4
Fortuity Index=25% bin 5
Serendipity Index=10% bin 3
Fluke Index=7% bin 2
Failure Index=14% bin 3
Loser Index=11% bin 3
Write-off Index=3% bin 2
Defeat Index=6% bin 2
Fiasco Index=30% bin 5
Debacle Index=3% bin 2
Blunder Index=2% bin 2
Catastrophe Index=12% bin 3
Turnip Index=-5% bin 1
Washout Index=1% bin 2
X
X
X
X
X
X
X
X
X
X
X
Condition on DHI index: Bins
𝑃(bin 3|𝑆) 𝑃(bin 3|𝐹)
-23%  index < 1% Bin 1
1%  index < 9% Bin 2
9%  index < 16% Bin 3
16%  index < 24% Bin 4
24%  index < 45% Bin 5
Use incidence rate.
Choice on how many bins and where to set transitions

11. What is the probability we see the observed DHI if
there is [not] oil in the ground
Bayesian inversion, page 11
Success Index=14%
Victory Index=21%
Triumph Index=11%
Sensation Index=16%
Glory Index=12%
Riches Index=14%
Fortune Index=18%
Fortuity Index=25%
Serendipity Index=10%
Fluke Index=7%
Failure Index=14%
Loser Index=11%
Write-off Index=3%
Defeat Index=6%
Fiasco Index=30%
Debacle Index=3%
Blunder Index=2%
Catastrophe Index=12%
Turnip Index=-5%
Washout Index=1%
X
X
X
X
X
X
X
X
X
X
X
Condition on DHI index: Model
𝑃(index = 14%|𝑆) 𝑃(index = 14%|𝐹)

12. Overview
Fundamental approach – Bayesian inversion
Formulation – Evidence and probable probabilities
Results

13. Evidence: A mathematical sleight of hand
• Probability
• 0 certain failure
• 1 certain success
• Bayes’ theorem
𝑃 𝑆|𝐷 =
𝑃 𝐷|𝑆
𝑃 𝐷|𝑆 𝑷 𝑺 + 𝑃 𝐷|𝐹 1 − 𝑷 𝑺
𝑷 𝑺
• Complicated function of prior
• Requires two numbers from database
• Evidence
• 𝑒 𝑆 = 10 log
𝑃 𝑆
1−𝑃 𝑆
• −∞ certain failure
• ∞ certain success
• Bayes’ theorem
𝑒 𝑆|𝐷 = 𝑒 𝑆 + 10log
𝑃 𝐷|𝑆
𝑃 𝐷|𝐹
• Simple, additive function of prior
• Single number captures effect of DHI data
Bayesian inversion, page 13

14. By working with evidence, a single number
captures the significance of your DHI data
Bayesian inversion, page 14
𝑃(𝑆)
𝑒(𝑆)
Δ(𝐷)
𝑒(𝑆|𝐷)
𝑃(𝑆|𝐷)

15. Probable probabilities
Bayesian inversion, page 15
Success Flat spot=“4”
Victory Flat spot=“3”
Triumph Flat spot=“5”
Sensation Flat spot=“2”
Glory Flat spot=“4”
Riches Flat spot=“1”
Fortune Flat spot=“5”
Fortuity Flat spot=“3”
Serendipity Flat spot=“2”
Fluke Flat spot=“1”
Failure Flat spot=“4”
Loser Flat spot=“2”
Write-off Flat spot=“3”
Defeat Flat spot=“4”
Fiasco Flat spot=“2”
Debacle Flat spot=“1”
Blunder Flat spot=“3”
Catastrophe Flat spot=“2”
Turnip Flat spot=“3”
Washout Flat spot=“1”
X
X
X
X
X
X
X
X
X
X
Counting only really works if you have a very large number of
prospects and a large number in each category
Treat incident rates as evidence for a certain level of probability
𝑃(flat spot = "3"|𝑆)
X
𝑃(flat spot = "3"|𝐹)
Score Total Success Failure
1 10 1 9
2 25 7 18
3 50 25 25
4 40 28 12
5 20 18 2
145 79 66 Probability distribution over evidence
implied by each score

16. Overview
Fundamental approach – Bayesian inversion
Formulation – Evidence and probable probabilities
Results

17. The evidence implied by a single indicator tells you
about the significance and reliability of that indicator
Bayesian inversion, page 17
Δ(𝐷)
𝐷

18. Binning the DHI index works best with around 5
bins and by partitioning samples, not the index
Bayesian inversion, page 18

19. Model based inference works well for mid-range
indices, but falls apart at the extremes
Bayesian inversion, page 19

20. Hybrid approach uses continuous model where it
agrees with binning
Bayesian inversion, page 20