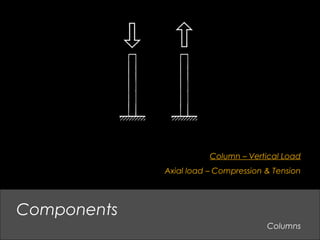
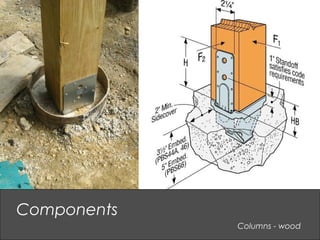
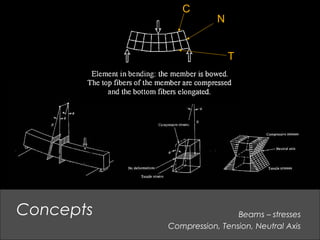
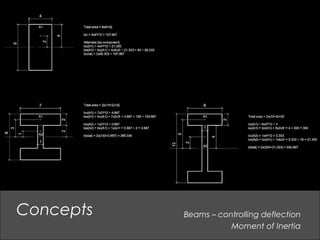
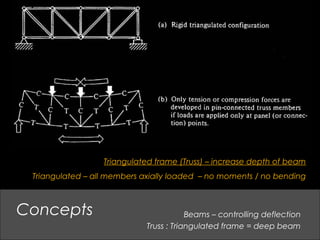
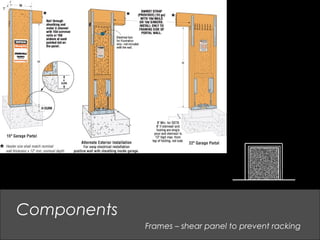
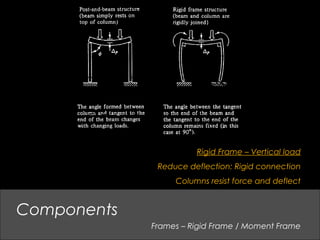
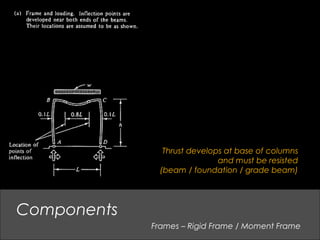
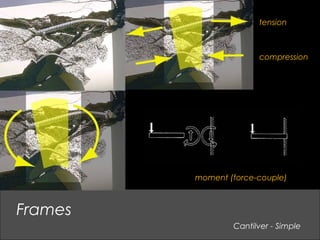
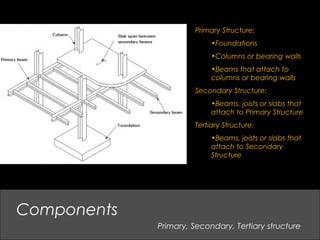
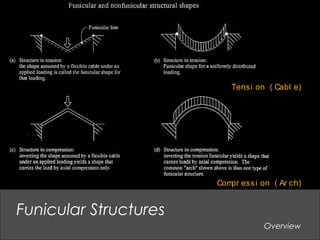
This document provides an overview of basic structural theory concepts including vertical, lateral and rotational forces. It discusses common structural components like columns, beams, frames and connections. It also covers common building materials like wood, steel and concrete. Specific structural concepts are explained like stresses in beams, controlling deflection, moment of inertia. Examples of structural failures are also mentioned.