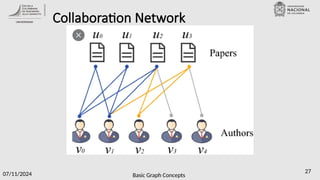
The document provides an overview of basic graph concepts, explaining the differences between graphs and networks, types of graphs, and key terminology across various fields. It details mathematical representations such as adjacency matrices and lists, as well as properties like degree distribution and clustering coefficients. The discussion also touches on historical examples like the Seven Bridges of Königsberg and relevant theories in network science.



































![Basic Graph Concepts
07/11/2024 37
Clustering coefficient:
what fraction of your neighbors are connected?
Node i with degree ki
Ci in [0,1]
Network Science: Graph Theory
CLUSTERING COEFFICIENT
Watts & Strogatz, Nature 1998.
Link to Model](https://image.slidesharecdn.com/basicgraphconcepts-241107143606-c8795a9e/85/Basic-Graph-gRAPH-CONCEPTS-ANDConcepts-pptx-37-320.jpg)










