(1) The document provides calculations to determine the required base plate thickness for a column base connection according to Eurocode standards. It includes input parameters such as column forces, material properties, bolt sizes and locations. (2) Three equations are solved simultaneously to determine the maximum pressure under the base plate, tension in the hold down bolts, and active concrete area. (3) The calculated pressure and bolt tension exceed design values, requiring a redesign of the base plate length/width or use of higher strength concrete. (4) The minimum required base plate thickness is then calculated based on the design bending moment and material yield strength.

1. COMPANY NAME Calculation No.
CALCULATION NUMBER
CALCULATION SHEET Project No.
© onlinestructuraldesign.com PROJECT NUMBER
Project Title: Project Name Calc. By Date Rev.
Author today 0
Subject/Feature: Column Base Plate Calculation Checked By Date Rev.
Checker today 0
Column Base Plate Calculation per EN 1992-1-1, EN 1993-1-1 and EN 1993-1-8
Input Output
Base plate size in plan Base plate thickness
Column base forces Max. pressure under baseplate
Materials (steel, concrete, bolts) Max. tension in bolts / bolt verifica on
Profile dimensions HEA340
h = 304.8 mm profile height
b = 304.8 mm profile width
Base Plate Dimensions
H = 600 mm
B = 600 mm
a = 0.95
Base plate thickness is determined in the calcula on
s = 155.22 mm
Bolt loca ons on plate
f = 241.3 mm
NB = 4 number of bolts
φ = 20 mm bolt diameter
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
1 of 7 6/11/2013 10:40 PM

2. Materials
Steel bolt characteris cs per EN 1993-1-8
Bolt class 4.6 Sec on 3 Table 3.1
bolt classes recommended by the Eurocode;
Bold yield strength The Na onal Annex may exclude certain bolt classes.
fyb = 240 N/mm2
Par al factor for steel bolts per EN 1993-1-8
γM2 = 1.25 Sec on 2 Table 2.1
par al safety factors recommended by the Eurocode;
Bolt design strength fyd = fy / γM2 Numerical values for safety factors may be defined
fyd-b = 192.0 N/mm2
in the Na onal Annex
Steel base plate characteris cs
Steel grade S 235
Steel yield strength
fy = 235 N/mm2
for thickness under 40mm
fy = 215 N/mm2
for thickness between 40mm and 80mm
Par al factor for steel elements (in bending) per EN 1993-1-1
γM0 = 1.00 Sec on 6.1 (1) and Note 2B
value recommended by the Eurocode; value to be used
can be found in the Eurocode Na onal Annexes
Steel modulus of elas city per EN 1993-1-1
Es = 210000 N/mm2
Sec on 3.2.6 (1)
Concrete characteris cs
Concrete class C12/15 per EN 1992-1-1:2004
fck = 12 MPa concrete characteris c cylinder strength Sec on 3 Table 3.1
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
2 of 7 6/11/2013 10:40 PM

3. References:
Design of Welded Structures - O. W. Blodge (James F. Lincoln Arc Welding Founda on)
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
COMPANY NAME Calculation No.
CALCULATION NUMBER
CALCULATION SHEET Project No.
© onlinestructuraldesign.com PROJECT NUMBER
Project Title: Project Name Calc. By Date Rev.
Author today 0
Subject Column Base Plate Calculation Ckd. By Date Rev.
Checker today 0
Par al factor for concrete for ul mate limit states per EN 1992-1-1:2004
Sec on 2 Table 2.1N
γc = 1.5 values for Persistent & Transient design situa ons
recommended by the Eurocode; values to be used
may be found in the Eurocode Na onal Annexes
Design compressive concrete strength per EN 1992-1-1:2004
Sec on 3.1.6 & Formula 3.15
acc = 1 Coefficient taking account of long term effects
fcd = acc * fck / gc = 8.00 MPa on the compressive strength and of unfavourable
effectsresul ng from the way the load is applied
value may be found in the EC Na onal Annex
Concrete modulus of elas city
Ecm = 27 GPa for concrete class C12/15 per EN 1992-1-1:2004
Sec on 3.1.3 Table 3.1
Aggregates = quartzite Sec on 3.1.3 (2)
Values in Table 3.1 are given for quartzite aggregates
Ecm = 27 GPa for concrete with quartzite aggregates Values for limestone and sandstone are reduced by 10%
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
3 of 7 6/11/2013 10:40 PM

4. Ecm = 27000 N/mm2
and 30% respec vely. For basalt aggregates the value
should be increased by 20%
Column base forces
N = 1000 kN axial force pair of column base forces. Mx and My are not
M = 380 kN*m bending moment considered simultaneous.
e = M/F = 380.0 mm
H/6 = 100.00 mm eccentricity
e > H/6 => Baseplate with large eccentricity
Three equa ons, three unknowns: Fb, Y, sc
(Axial force in steel hold down bolts, ac ve area under base plate,
maximum pressure under base plate)
1. Forces equilibrium
Y*sc/2 - Fb -N = 0
Fb + N = Y*sc*B/2 (1)
2. Bending moment equilibrium
Fb * f + (Fb + N) * (H/2 - Y/3) - N * e = 0
Fb = -N * (H/2 - Y/3 -e)/(H/2 - Y/3 + f) (2a)
N = -Fb * (H/2 - Y/3 -e)/(H/2 - Y/3 + f) (2)
3. Represen ng the elas c behaviour of the concrete
support and the steel hold-down bolt:
a/b = eb/ec = (sb / Es) / (sc / Ec)
since Es = sb / es modulus of elas city of steel bolt
Ec = sc / ec modulus of elas city of concrete
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
4 of 7 6/11/2013 10:40 PM

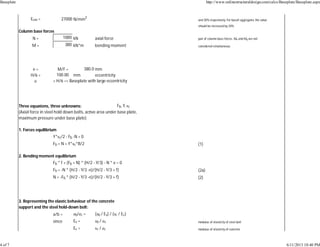
5. nb = 2 number of steel hold down bolts
Ab = 2* π*φ2
/4 = 628.3 mm2
area of steel hold down bolts
sb = Fb / Ab
n = Es / Ec = 7.78 modular ra o of elas city, steel to concrete
References:
Design of Welded Structures - O. W. Blodge (James F. Lincoln Arc Welding Founda on)
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
COMPANY NAME Calculation No.
CALCULATION NUMBER
CALCULATION SHEET Project No.
© onlinestructuraldesign.com PROJECT NUMBER
Project Title: Project Name Calc. By Date Rev.
Author today 0
Subject Column Base Plate Calculation Ckd. By Date Rev.
Checker today 0
a/b = (N/Ab)/(sc*n) = N/(Ab*sc*n)
From similar triangles =>
a/b = (H/2-Y+f)/Y
=> N/(Ab*sc*n) = (H/2-Y+f)/Y =>
=> sc = Fb * Y / (Ab * n *(H/2 - Y + f)) (3)
From (1), (2) and (3)
-Fb * (H/2 - Y/3 -e)/(H/2 - Y/3 + b) + Fb = (Fb * Y2
* B) / [2 * Ab * n *(H/2 - Y + f)]
Solve for Y:
Y3
+ 3 * (e - H/2) * Y2
+ [(6 * n * Ab)/B] * (f + e) * Y - [(6 * n * Ab)/B] * (H/2 + f) * (f + e) = 0
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
5 of 7 6/11/2013 10:40 PM

6. or
Y3
+ K1 * Y2
+ K2 * Y + K3 = 0
where
K1 = 3 * (e - H/2) = 240
K2 = [(6 * n * Ab)/B] * (f + e) = 30362
K3 = - K2 * (H/2 + f) = -16435192
Y = 166.5 mm
Fb = 278.92 kN (in 2 bolts ) per (2a) hold down bolts max. tension (in all bolts)
F1.bolt = Fb /2 = 139.46 kN hold down bolt max. tension - in 1 bolt
F1.bolt /(π*φ2
/4) = 443.92 N/mm2 > fyd-b redimension, bolt effec ve stress is larger than bolt design stress
192.0 N/mm2
sc = 25.35 MPa per (3)
sc > fcd fcd = 8.00 MPa effec ve max. pressure under baseplate is compared
redesign base plate length and/or width with the concrete design compressive strength
stress under base plate is larger than the concrete compressive capacity if the max. pressure is higher than the concrete
Design of the Base Plate Thickness
Cri cal sec on loca on
s = 155.22 mm
Stress at the cri cal sec on loca on
ssc = sc*(Y - s) / Y = 1.72 MPa
Design cri cal moment - at cri cal sec on
MEd.plate = [(σsc*s/2)*(s/3)+(σc*s/2)*(s*2/3)]*B 126.31 kN*m
MC,Rd = Mpl,rd = (Wpl * fy)/ γM0 (4)
per EN 1993-1-1
Sec on 6.2.5 (2) Formula 6.13
Design resistance for bending for bending about one
principal axis for class 1 or 2 cross sec ons
Plas c sec on modulus of rectangular sec ons
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
6 of 7 6/11/2013 10:40 PM

7. Wpl = B*tpl
2
/4 (5)
(tpl = base plate thickness)
from (4) and (5) => [fy * (B*tpl
2
)/4]/ γM0≥ MEd.plate
=> tpl≥ √[4 * MEd.plate * γM0 / (B * fy)]
=> tpl≥ 62.58 mm (with fy = 215 N/mm2
)
References:
Design of Welded Structures - O. W. Blodge (James F. Lincoln Arc Welding Founda on)
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
Baseplate http://www.onlinestructuraldesign.com/calcs/Baseplate/Baseplate.aspx
7 of 7 6/11/2013 10:40 PM