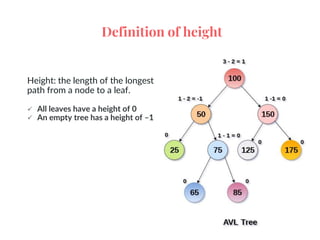
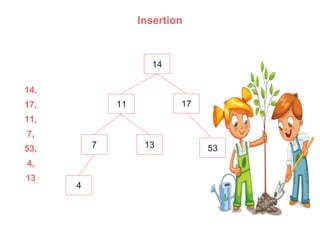
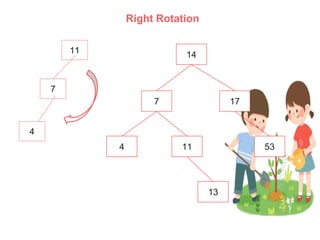
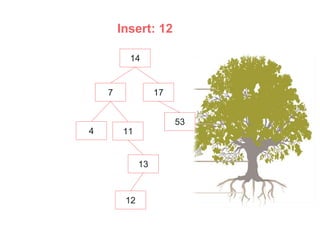
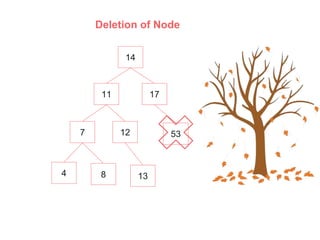
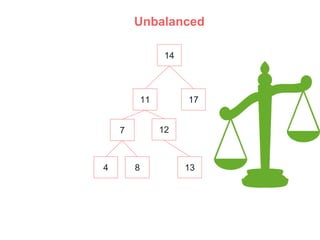
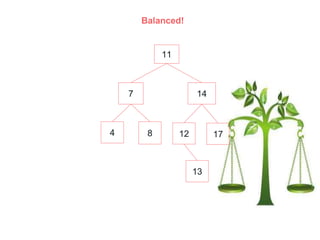
An AVL (Adelson-Velskii & Landis) tree is a self-balancing binary search tree where the height difference between subtrees is at most one, ensuring O(log n) time complexity for lookup, insertion, and deletion operations. It employs rotations to maintain balance during inserts and deletes, including left, right, left-right, and right-left rotations. The document illustrates insertion and deletion processes, demonstrating how to rebalance the tree as necessary.

1. AVL (Adelson-Velskii
& Landis) Tree
.
Presented By
Sana Rahim

2. AVL Tree
A balanced binary search tree where
the height of the two subtrees
(children) of a node differs by at most
one. Look-up, insertion, and deletion
are O( log n), where n is the number of
nodes in the tree

3. Definition of height
Height: the length of the longest
path from a node to a leaf.
 All leaves have a height of 0
 An empty tree has a height of –1

4. AVL Rotations
To balance itself, an AVL tree may perform the following four
kinds of rotations
• Left rotation
• Right rotation
• Left-Right rotation
• Right-Left rotation

5. Insertion
14
17
11
7 53
4
14,
17,
11,
7,
53,
4,
13
13

6. 14
17
7
4 53
11
13
Right Rotation
11
7
4

7. Insert: 12
14
17
7
4
53
11
13
12

8. First left Rotation then Right:
14
17
7
4
53
11
12
13

9. AVL tree is balanced.
14
17
7
4 53
12
13
11

10. Deletion of Node
14
17
7
4
53
11
12
8 13

11. Unbalanced
14
17
7
4
11
12
8 13

12. Balanced!
14
17
7
4
11
12
8
13

13. Questions