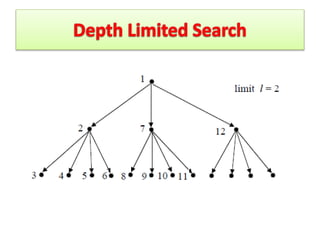
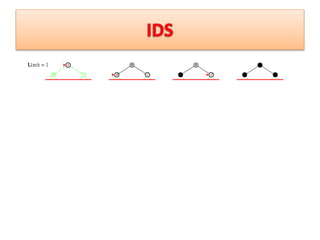
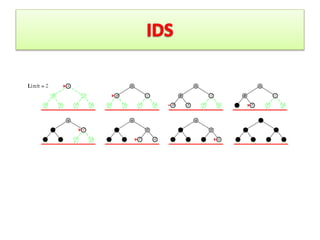
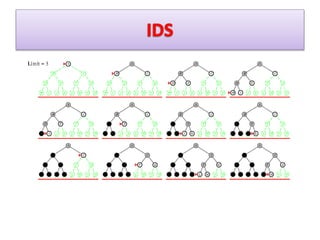
DLS limits the depth of a DFS search to guarantee termination. If a goal state exists at a depth less than L, DLS will find it but not necessarily an optimal path. The space complexity is O(bl) and time is O(bl). IDS improves on DLS by repeatedly running DLS with increasing depth limits, making it complete, optimal, and with better time (O(bd)) and space (O(bd)) complexities than plain DFS or BFS.

1. Submitted to MAM SADIA SAHAR
SUBMITTED BY AMARA MUSARAT, AMNA
ASHRAF, REDA SHAHEEN, RIDA MARIAM,
SADIA MUNAWAR, SAYYEDA UMMARA,
SAIMINA FALAK SHER

2. • DLS is a variation of DFS. If we put a limit l on
how deep a depth first search can go,
• we can guarantee that the search will
terminate (either in success or failure).

4. • If there is at least one goal state at a depth
less than L, this algorithm is guaranteed to
find a goal state, but it is not guaranteed to
find an optimal path.
• The space complexity is O(bl), and the time
complexity is O(bl).
• For most problems we will not know what is a
good limit L until we have solved the problem!

5. • If L < D (solution depth) then it will be
incomplete. Difficult to know D. If L > D, may
be non-optimal.
• L can be set from knowledge of a domain.
• The search is limited to a predefined depth.
• The depth of each state is recorded as it is
generated. When picking the next state to
expand, only those with depth less or equal
than the current depth are expanded.

6. • IDS is a variation of DLS.
• Combines the benefits of depth-first and
breadth-first search.
• It is complete and optimal.
• It has time complexity of O(bd).
• But space complexity is only O(bd).

7. • Depth-limited search, with
– depth = 0
– then again with depth = 1
– then again with depth = 2
– ... until you find a solution

12. • Complete?
– Yes
• Time?
– The time complexity is O(bd) as in BFS, which is
better than DFS.
• Space?
– The space complexity is O(bd) as in DLS with l=d,
which is better than BFS.
• Optimal?
– Yes, if step cost = 1