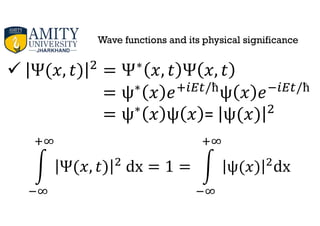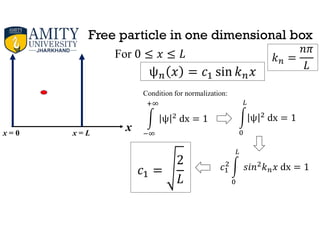
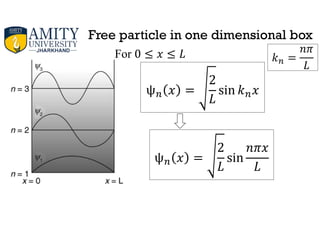
1) The document discusses wave functions and their physical significance in quantum mechanics. It describes how the probability of finding a particle between two positions x=a and x=b is given by the integral of the wave function. 2) As an example, it analyzes the quantum mechanical problem of a free particle confined to a one-dimensional box between x=0 and x=L. It shows that the wave function and energy levels become quantized due to the boundary conditions at the walls. 3) The energy levels are En = (nπħ/L)2, where n=1,2,3..., corresponding to the ground, first excited, second excited and higher energy states.

1. Module 1: Applied Quantum Mechanics
Dr Biplab Bag
Assistant Professor, Physics

2. Wave functions and its
physical significance
 Generally, Ψ(x,t) is a complex function, and it does not
directly provide any information on the position,
momentum, etc. of the particle.
• However, the quantity, ∫ Ψ∗
Ψ dx = ∫ Ψ dx
represents the probability of finding the particle
between x = a to x = b.
= + ∗
= − ∗
= +
Now, how does a wave function represent a particle?

3. Wave functions and its physical significance
Ψ( , ) dx = 1
Condition for normalization
Ψ , = ψ = ψ /ħ
 Ψ( , ) = Ψ∗
, Ψ ,
= ψ∗ /ħ
ψ /ħ
= ψ∗
ψ = ψ( )

4.  Ψ( , ) = Ψ∗
, Ψ ,
= ψ∗ /ħ
ψ /ħ
= ψ∗
ψ = ψ( )
Wave functions and its physical significance
Ψ( , ) dx = 1 = ψ( ) dx

5. Wave functions and its physical significance
1.ψ( )is always continuous, and
2.
( )
is continuous except at points where
the potential is infinite.

6. Free particle in one dimensional box
x
x = 0 x = L
= 0 if 0 ≤ ≤
= ∞ otherwise
 → ∞, ⇒ ψ = 0
For, 0 ≥ ≥
−
ħ
2
ψ
+ ( )ψ = ψ
TIDSE
ψ = 0
to have finite value

7. Free particle in one dimensional box
x
x = 0 x = L
= 0 if 0 ≤ ≤
= ∞ otherwise
 For,0 ≤ ≤
−
ħ
2
ψ
+ ( )ψ = ψ
TIDSE
ψ = 0
−
ħ
2
ψ
= ψ
ψ
= −
2
ħ
ψ

8. Free particle in one dimensional box
x
x = 0 x = L
= 0 if 0 ≤ ≤
= ∞ otherwise
For 0 ≤ ≤
ψ
=
0
ψ
= −
2
ħ
ψ
ψ
= −k ψ
k =
2
ħ
=
ħ k
2
General Solution:
ψ = sin + cos
ψ = +

9. Free particle in one dimensional box
x
x = 0 x = L
= 0 if 0 ≤ ≤
= ∞ otherwise
For 0 ≤ ≤
ψ
=
0
=
ħ k
2
ψ = sin + cos
(i)ψ = 0 = 0
(ii)ψ = = 0
Boundary
Condition
To match the condition (i), we should have c2= 0
ψ = sin
So Now,

10. Free particle in one dimensional box
= 0 if 0 ≤ ≤
= ∞ otherwise
For 0 ≤ ≤
=
ħ k
2
(i)ψ = 0 = 0
(ii)ψ = = 0
ψ = sin
Using the condition (ii), we have
ψ = = 0 = sin
sin = 0 =
=
Allowed values of ’s are , , … and so on

11. Free particle in one dimensional box
= 0 if 0 ≤ ≤
= ∞ otherwise
For 0 ≤ ≤
=
ħ k
2
(i)ψ = 0 = 0
(ii)ψ = = 0
=
Allowed values of ’s are , , … and so on
Hence, is quantized
=
ħ
2 L
Hence, is also quantized
“Flavour oF Quantum mechanics”
n = 1, 2, 3, 4….
ψ = sin

12. Free particle in one dimensional box
For 0 ≤ ≤
=
ħ
2 L
n = 1, 2, 3, 4….
n = 1
n = 2
n = 3
n = 4
Ground State
First Excited State
Second Excited State
Third Excited State

13. Free particle in one dimensional box
For 0 ≤ ≤
ψ = sin
=
ψ dx = 1
Condition for normalization:
x
x = 0 x = L
ψ dx = 1
dx = 1
=
2

14. Free particle in one dimensional box
For 0 ≤ ≤
ψ =
2
sin
=
ψ =
2
sin