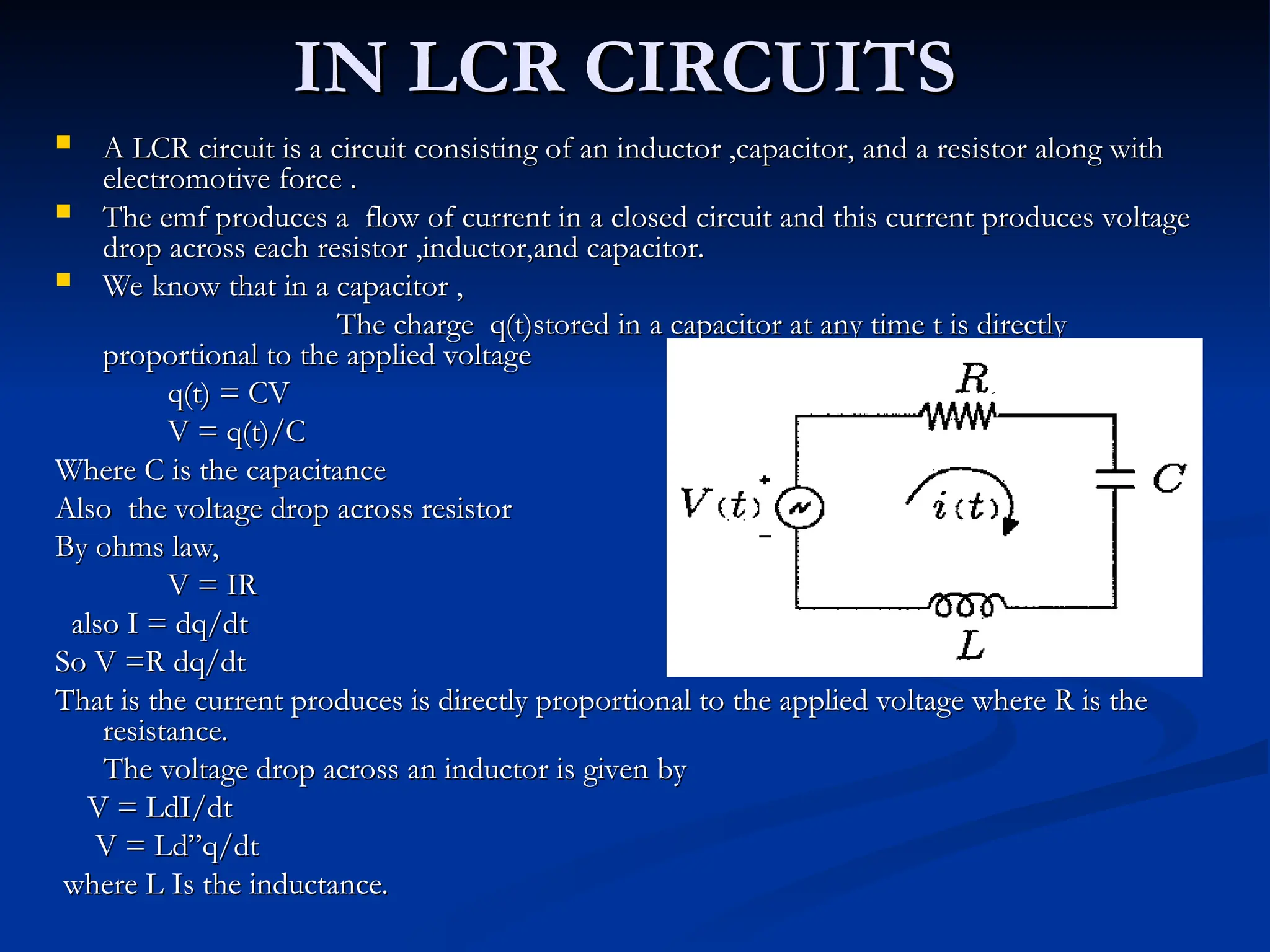
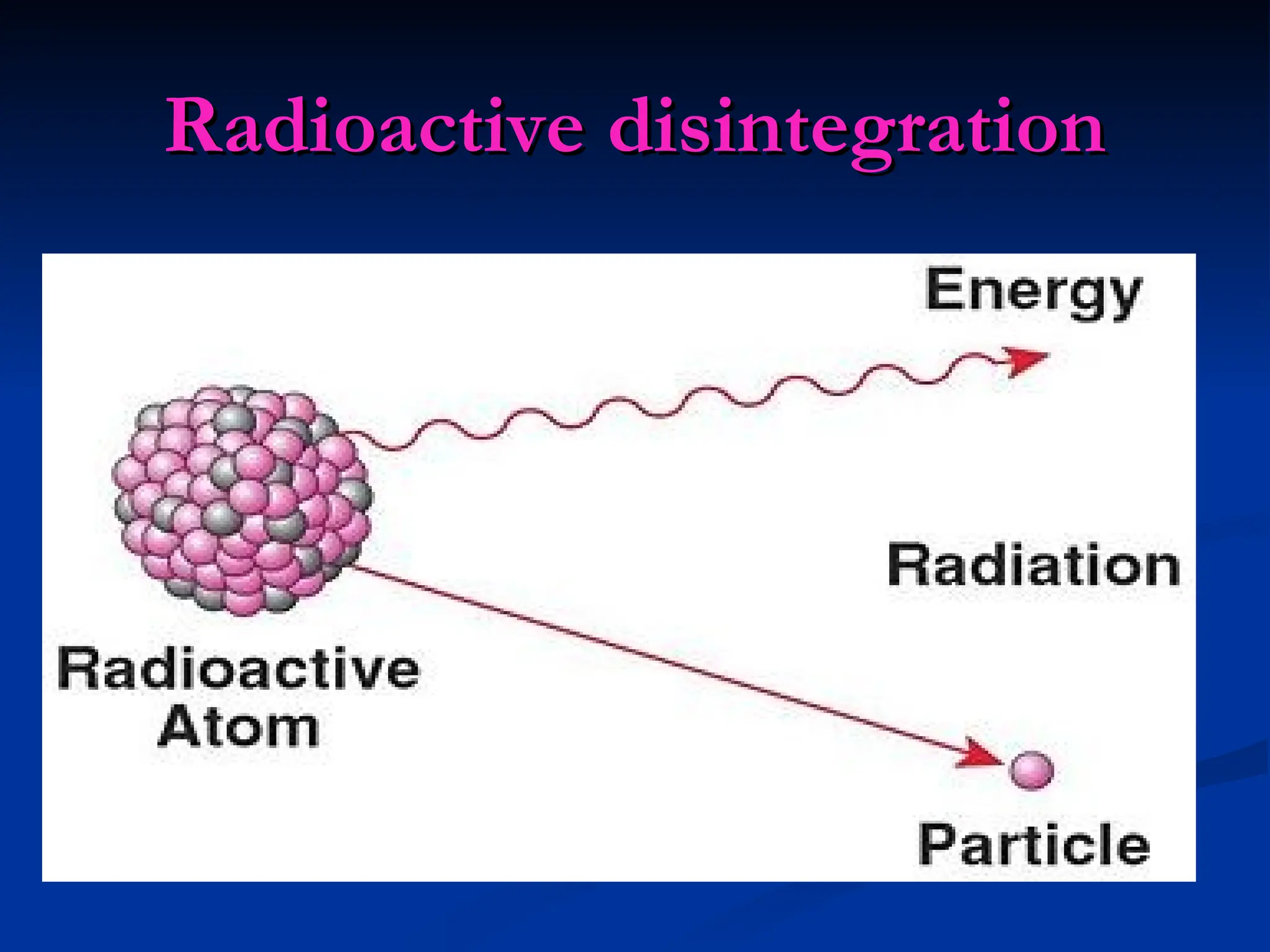
The document discusses the fundamentals of differential calculus, including its definition, applications, and classifications based on independent variables and derivative order. It highlights real-world applications, such as projectile motion and LCR circuits, and explains the mathematical basis of Newton's laws and radioactive decay through differential equations. The detailed breakdown of mathematical formulas and principles provides insights into how derivatives express rates of change in various physical phenomena.