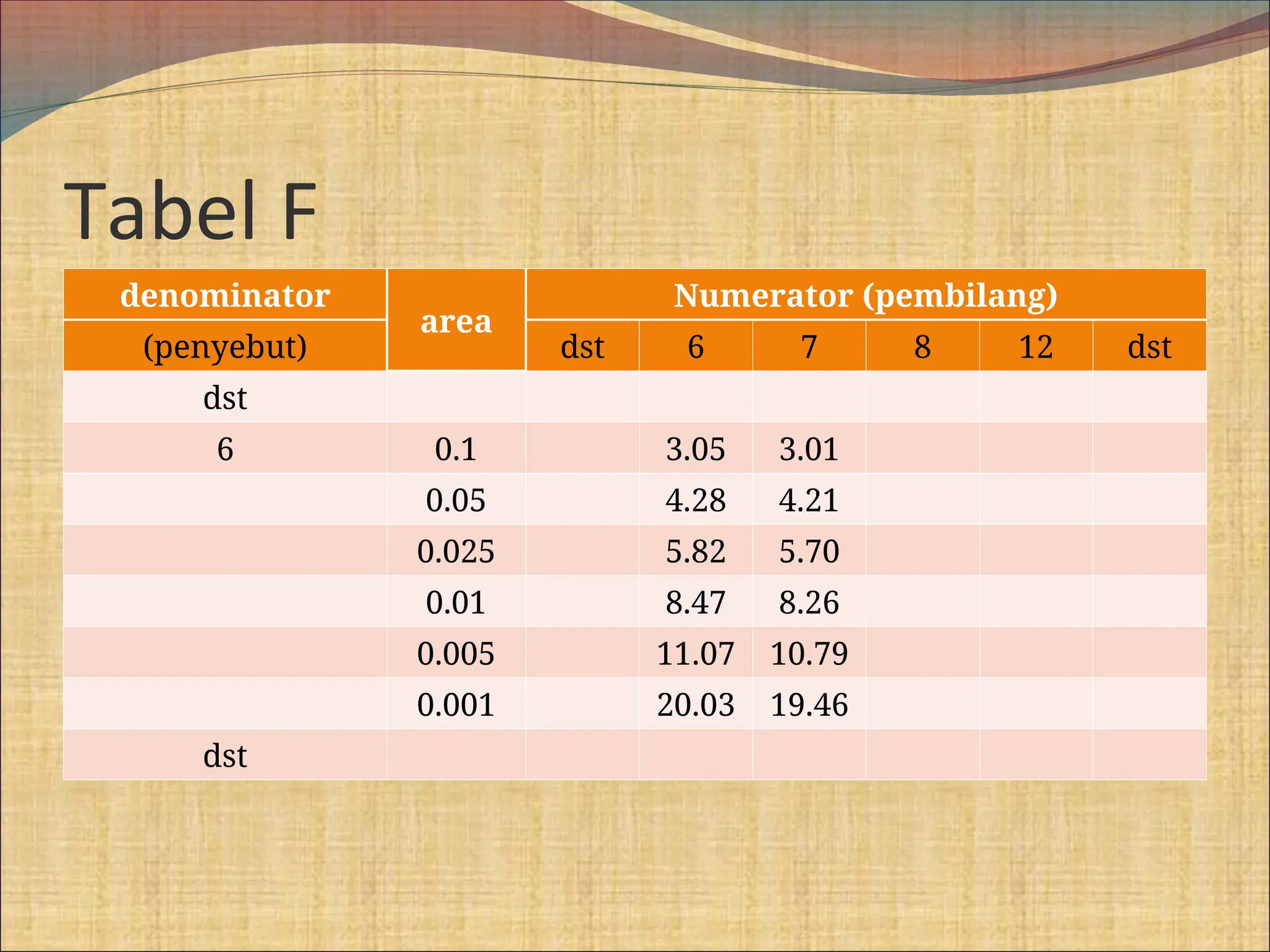
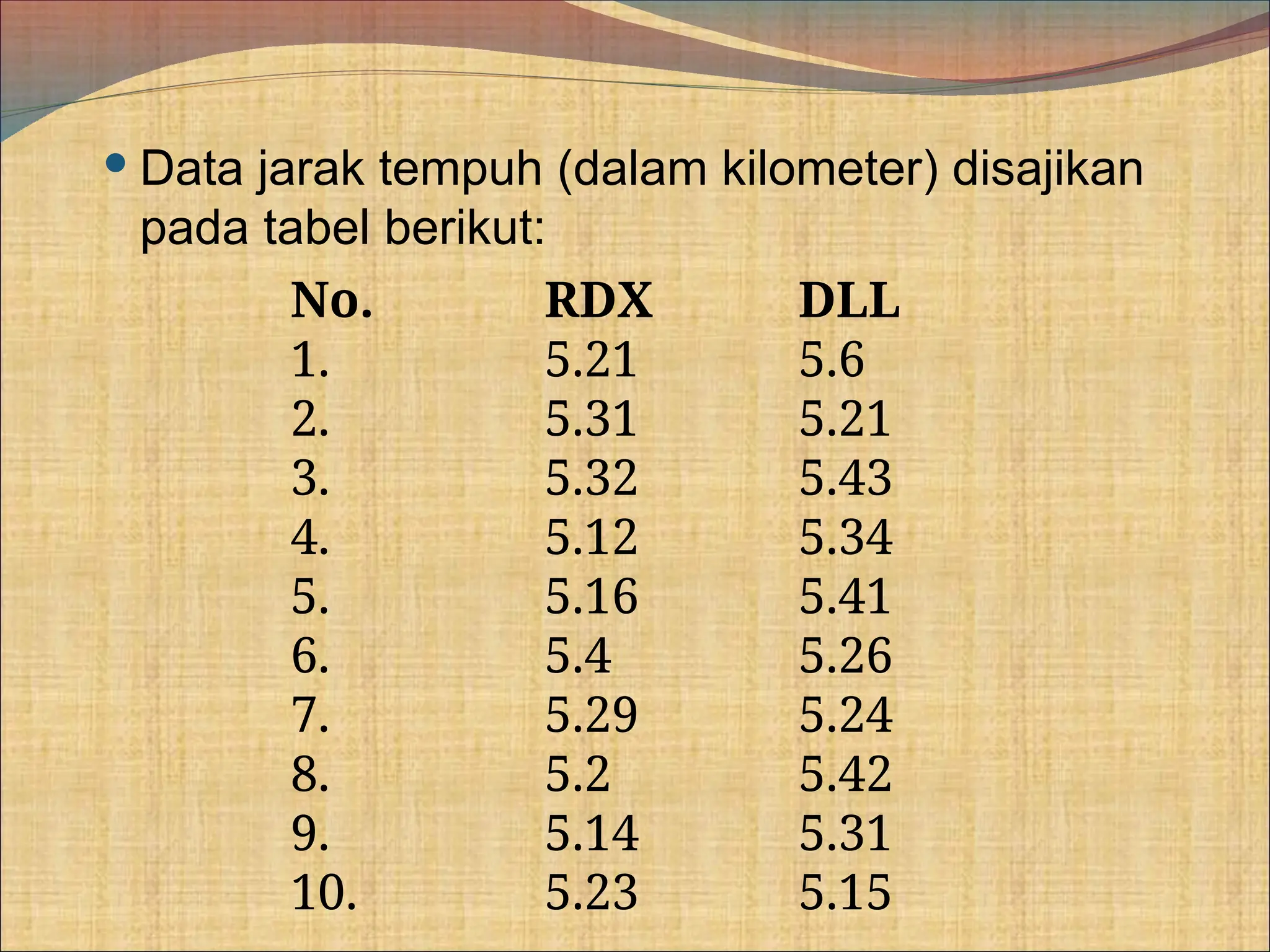
Dokumen ini membahas berbagai metode statistik untuk menguji perbedaan rata-rata antara populasi dan sampel, termasuk uji z, uji t independen, dan uji t berpasangan. Contoh kasus yang diberikan melibatkan pengujian kadar kolesterol pada pasien hipertensi dan efektivitas obat baru pada gangguan tidur. Selain itu, dokumen ini menjelaskan pentingnya asumsi normalitas dan homogenitas ragam dalam analisis statistik.

2. Uji Z (diambil dep FKK FKUI)
 Menguji beda mean satu sampel
 Mengetahui perbedaan mean populasi dengan
mean data sampel penelitian
 Membandingkan data satu sampel dengan data
populasinya
 Harus diketahui nilai mean dan SD data populasi
(μ dan σ)

Keterangan:
= mean data sampel
μ = mean data populasi
σ = SD data populasi
N = jumlah sampel yang diteliti

3.  Diketahui kadar kolesterol orang dewasa normal
adalah 200 mg dengan SD sebesar 56 mg. Seorang
peneliti telah melakukan pengukuran kadar
kolesterol pasien hipertensi sebanyak 49 orang.
Didapatkan mean kolestrol mereka adalah 220
mg. Peneliti ingin menguji apakah kadar
kolesterol pasien hipertensi berbeda dengan
kadar kolesterol orang dewasa normal?
 Kadar kolesterol normal adalah mean populasi: μ
= 200 mg
 SD populasi: σ = 56 mg
 Mean kadar kolesterol sampel/pasien
hipertensi: = 220 mg

4.  Ho = tidak ada perbedaan rata-rata kadar
kolesterol orang dewasa normal dengan
penderita hipertensi
 H1 = ada perbedaan rata-rata kadar kolesterol
orang dewasa normal dengan penderita
hipertensi  2 tail (2 arah)
 Batas signifikansi 5% (α = 0.05)
 Z = 220 – 200
 56/√49
 = 2,50

5. Tabel Standar Kurva Normal
Z 0 0.01 0.02 dst
0
0.1
...
...
2.5 0.4938 0.494
2.6 0.4953

6.  Dari nilai Z=2,50 diperoleh peluang adanya
perbedaan di populasi = 0,4938  berarti nilai p
(peluang perbedaan terjadi karena kebetulan) =
0,5 - 0,4938 = 0,0062
 Nilai peluang pada tabel kurva normal mrp nilai
1 tail. Sedangkan arah uji ini adalah 2 arah
 Jadi nilai p untuk uji ini = 2 x 0,006 = 0.012
 Nilai p kemudian dibandingkan dg nilai α =
0.05, maka terlihat bahwa p<0.05
 Jadi diputuskan bahwa H0 ditolak  H1 diterima
 Disimpulkan bahwa pada α = 5%, maka secara
statistik kadar kolesterol orang hipertensi
berbeda dengan kadar kolesterol orang dewasa

7.  α = 5%  α/2 = (5/2)% = 2,5% = …..
 1 - …… = ………
 …………> Z > ……….

9. Uji beda 2 mean
 Independen (tidak berpasangan): data kelompok
yang satu tidak mempunyai ketergantungan
dengan data kelompok kedua
 Membandingkan kolesterol pasien rawat kelas III
dan kelas I RSCM
 Dependen = berpasangan, data yang satu mpy
ketergantung an dengan data lainnya
 Bb sebelum dan sesudah mengikuti program diet
 berasal dari orang yang sama

10.  Uji yang bisa dilakukan:
 Uji t  digunakan tabel probabilitas t
 Uji F  digunakan tabel probabilitas F
 Uji t independen (sampel bebas)
 Variabel yang dihubungkan berbentuk numerik
dan kategorik
 Data berdistribusi normal
 Kedua klp data independen
 Perlu dilihat ada tidaknya perbedaan variasi
kedua klp data (uji homogenitas varians)

11. Uji homogenitas varians (F)
df1 = n1-1 df2 = n2-1
Varians atau Sd yang lebih besar sebagai
(numerator) pembilang dan varians atau Sd yang
lebih kecil sebagai (denominator) penyebut
P < 0.05  varians berbeda
P > 0.05  varians sama

12. Tabel F
denominator
area
Numerator (pembilang)
(penyebut) dst 6 7 8 12 dst
dst
6 0.1 3.05 3.01
0.05 4.28 4.21
0.025 5.82 5.70
0.01 8.47 8.26
0.005 11.07 10.79
0.001 20.03 19.46
dst

13. Uji t independen untuk varian sama

14. Tabel T
Df/p 0.1 0.05 0.025 0.01 0.005
1
2
3
4
9 1.383 1.833 2.262 2.821 3.250
12 1.356 1.782 2.179 2.681 3.055
dst

15. Uji t independen (sampel bebas)
 Apakah ada perbedaan tinggi badan antara pria
dan wanita
 Klp pria dan wanita adalah klp independen
 Jenis kelamin: kategorik
 Tinggi badan: numerik (mean= 162,3; SD=8,44)
 Distribusi IMT: normal
 Uji homogenitas varian (uji F)
 Ho=varian TB di kedua klp sama
 H1=varian TB di kedua klp berbeda

16.  Uji varians p>0.05  Ho diterima
 Uji varians p<0.05  Ho ditolak, H1 diterima

18.  Dari hasil SPSS

19.  Jika dalam penelitian ditemukan adanya
perbedaan diantara 2 sampel, maka perbedaan
tsb memiliki 2 kemungkinan:
1.Perbedaan yang signifikan
2.Perbedaan yang tidak signifikan
• Teknik yang digunakan adalah t-test dan chi-
square
• Apabila data berasal dari distribusi yang lebih
dari 2 buah, maka digunakan teknik analisis
varian/Anava

20. Teknik t-test
 Untuk menguji signifikansi perbedaan 2 buah mean yang berasal dari 2 buah distribusi
 Rumus:
 Keterangan:
Mean pada distribusi sampel 1
Mean pada distribusi sampel 2
Nilai varian pada distribusi sampel 1
Nilai varian pada distribusi sampel 2
Jumlah ind pd sampel 1
Jumlah ind pd sampel 1

21.  Jika disederhanakan:
 SDbm adalah standar kesalahan perbedaan mean,
dari rumus:

22.  Penelitian tentang perbedaan stress kerja ditinjau
dari jenis kelamin karyawan di perusahaan ABC.
SSK pd karyawan laki-laki (X) dan permpuan (Y).
X1 X2 X12 X22
78 63 6084 3969
56 58 3136 3364
64 32 4096 1024
71 54 5041 2916
62 64 3844 4096
59 43 3481 1849
62 62 3844 3844
452 376 29526 21062
n = 7 n = 7

23.  Hitung: db = N-2

24. UJI T 2-SAMPEL INDEPENDEN
(INDEPENDENT 2-SAMPLE T-TEST)

25.  digunakan untuk menguji kesamaan rata-rata dari
2 populasi yang bersifat independen, dimana
peneliti tidak memiliki informasi mengenai ragam
populasi.
 Independen maksudnya adalah bahwa populasi
yang satu tidak dipengaruhi atau tidak
berhubungan dengan populasi yang lain.
 Barangkali, kondisi dimana peneliti tidak memiliki
informasi mengenai ragam populasi adalah
kondisi yang paling sering dijumpai di kehidupan
nyata.
 Oleh karena itu secara umum, uji-t (baik 1-sampel,
2-sampel, independen maupun paired) adalah
metode yang paling sering digunakan.

26. Contoh kasus:
 Sebuah perusahaan penghasil bahan bakar mobil hendak memilih
satu dari 2 ramuan kimia yang akan dijadikan campuran di dalam
produknya. Ramuan tersebut adalah RDX dan DLL.
 Untuk memutuskannya, departement riset perusahaan tersebut
mengadakan penelitian untuk menguji efisiensi penggunaan bahan
bakar setelah diberi kedua campuran tersebut.
 Dalam penelitian ini, digunakan 20 buah mobil yang memiliki
karakteristik yang homogen.
 Dari 20 mobil, sepuluh diantaranya diberi bahan bakar dengan
campuran RDX dan sepuluh mobil sisanya diberi bahan bakar
dengan campuran DLL.
 Keduapuluh mobil kemudian dijalankan oleh 20 orang pengemudi
dengan kemampuan mengemudi yang homogen pada suatu lintasan
tertentu. Dengan memberikan 1 liter bahan bakar untuk setiap
mobil, jarak tempuh 10 mobil yang diberi bahan bakar bercampur
RDX dan 10 mobil dengan bahan bakar bercampur DLL kemudian
dicatat.

27. No. RDX DLL
1. 5.21 5.6
2. 5.31 5.21
3. 5.32 5.43
4. 5.12 5.34
5. 5.16 5.41
6. 5.4 5.26
7. 5.29 5.24
8. 5.2 5.42
9. 5.14 5.31
10. 5.23 5.15
 Data jarak tempuh (dalam kilometer) disajikan
pada tabel berikut:

28.  Yang perlu diperhatikan dalam kasus ini adalah:
1. Sebanyak 20 mobil yang memiliki karakteristik
homogen digunakan.
2. Keduapuluh mobil kemudian dibagi menjadi 2
grup, yaitu grup untuk mobil-mobil yang diberi
bahan bakar RDX dan grup untuk mobil-mobil
yang diberi bahan bakar DLL.
3. Kedua grup saling bebas satu sama lain.
4. Peneliti tidak memiliki informasi mengenai
ragam populasi dari data kedua grup.

29.  Sebelum berlanjut, marilah kita periksa apakah
data di atas menyebar normal atau tidak.
Apabila data tidak menyebar normal, maka uji-t
2-sampel tidak tepat diterapkan.
 Hipotesis uji kenormalan data adalah sebagai
berikut:
 H0 : Data menyebar normal
 H1 : Data tidak menyebar normal
 Hasil uji normalitas data dengan menggunakan
statistik uji Lilliefors (Kolmogorov-Smirnov)
disajikan di bawah ini ( α = 0.05):

30. Uji asumsi kenormalan data RDX:
 Lilliefors (KolmogorovSmirnov) normality test
data: RDX
D = 0.1354, pvalue = 0.8688
Uji asumsi kenormalan data DLL:
 Lilliefors (KolmogorovSmirnov) normality test
data: DLL
D = 0.143, pvalue = 0.8133
 Kesimpulan statistika untuk uji normalitas data RDX
dan DLL adalah TERIMA H0 , karena p-value > 0.05.
Dengan kata lain, kedua data menyebar normal.

31.  Perlu kita ketahui bahwa kasus di atas layak
dianalisis dengan uji-t 2-sampel independen
karena:
1. Kedua data menyebar normal
2. Dua sampel tersebut bersifat independen,
karena data RDX tidak dipengaruhi atau tidak
berhubungan dengan data DLL.
3. Peneliti tidak memiliki informasi mengenai
ragam populasi dari kedua sampel.

32.  Sebelum melakukan uji hipotesis kesamaan rata-
rata 2 populasi dengan uji-t 2-sampel
independen, ada pertanyaan yang perlu dijawab
yaitu apakah ragam populasi dari 2 sampel
diasumsikan homogen atau tidak.
 Hal ini penting untuk memutuskan apakah kita
menggunakan metode uji-t 2-sampel independen
dengan asumsi ragam kedua populasi
disumsikan homogen ataukah menggunakan
uji-t 2-sampel independen dengan asumsi
ragam kedua populasi tidak homogen.
 Perlu kita ketahui bahwa keduanya memiliki
rumus perhitungan yang berbeda.

33.  Untuk itu, asumsi homogenitas ragam populasi
dari 2 sampel ini perlu diuji terlebih dahulu.
 Hipotesis untuk uji homogenitas ragam populasi
adalah:
 H0 : σ2
RDX = 1
σ2
DLL
 H0 : σ2
RDX ≠ 1
σ2
DLL
 Untuk H0 berarti rasio ragam populasi dari
kedua sampel adalah 1.

34.  Hasil ujinya disajikan sebagai berikut:
 F test to compare two variances
 data: RDX and DLL
 F = 0.4084, num df = 9, denom df = 9, pvalue =
0.1984
 alternative hypothesis: true ratio of variances is
not equal to 1
 95 percent confidence interval:
 0.1014400 1.6442037
 sample estimates:
 ratio of variances
 0.4083969

35.  Kesimpulan statistika adalah TERIMA H0 ,
karena p-value > 0.05, sehingga kita dapat
mengasumsikan bahwa ragam populasi dari
kedua sampel adalah homogen.
 Untuk itu, metode yang tepat adalah uji-t 2-
sampel independen dengan asumsi ragam
populasi dari kedua sampel adalah homogen.
 Pada tahap ini, kita bisa langsung melakukan
analisis data dengan uji-t 2-sampel independen
dengan asumsi ragam populasi dari kedua
sampel adalah homogen.

36.  Hipotesisnya adalah:
 H0 : μRDX−μDLL=0
 H1 : μRDX−μDLL≠0
 Dapat pula ditulis:
 H0 : μRDX =μDLL
 H1 : μRDX≠μDLL
 Untuk H0 berarti rata-rata RDX sama dengan
rata-rata DLL.

37.  Hasil analisis disajikan seperti di bawah ini:
 Two Sample t-test
 data: RDX and DLL
 t = 1.7803, df = 18, pvalue = 0.09192
 alternative hypothesis: true difference in means is
not equal to 0
 95 percent confidence interval:
 0.20493187 0.01693187
 sample estimates:
 mean of x mean of y
 5.238 5.332

38.  Output di atas menunjukkan bahwa tidak terdapat cukup
bukti yang menyatakan bahwa rata-rata jarak tempuh mobil
yang menggunakan bahan bakar bercampur RDX dan DLL
berbeda.
 Dengan kata lain, rata-rata jarak tempuh mobil berbahan
bakar RDX dan DLL tidak berbeda nyata pada taraf nyata 5%.
 Perbedaan nilai rata-rata jarak tempuh mobil yang berbahan
bakar RDX (5.238) dan DLL (5.332) hanyalah bersifat kebetulan
semata.
 Sehingga, perusahaan dapat memilih salah satu dari ramuan
RDX ataupun DLL karena keduanya memiliki performance
yang sama.
 Software statistika yang digunakan untuk melakukan analisis data
dalam tulisan ini adalah software R version 2.6.2 for LINUXTM .
 R Development Core Team (2008). R: A language and environment
for statistical computing. R Foundation for Statistical Computing,
Vienna, Austria. ISBN 3900051070, URL http://www.Rproject.org.

39. UJI T BERPASANGAN
(PAIRED T-TEST)
 Uji-t berpasangan (paired t-test) adalah salah
satu metode pengujian hipotesis dimana data
yang digunakan tidak bebas (berpasangan).
 Ciri-ciri yang paling sering ditemui pada kasus yang
berpasangan adalah satu individu (objek
penelitian) dikenai 2 buah perlakuan yang berbeda.
 Walaupun menggunakan individu yang sama,
peneliti tetap memperoleh 2 macam data sampel,
yaitu data dari perlakuan pertama dan data dari
perlakuan kedua.

40.  Perlakuan pertama mungkin saja berupa
kontrol, yaitu tidak memberikan perlakuan sama
sekali terhadap objek penelitian.
 Misal pada penelitian mengenai efektivitas suatu
obat tertentu, perlakuan pertama, peneliti
menerapkan kontrol, sedangkan pada perlakuan
kedua, barulah objek penelitian dikenai suatu
tindakan tertentu, misal pemberian obat.
 Dengan demikian, performance obat dapat
diketahui dengan cara membandingkan kondisi
objek penelitian sebelum dan sesudah diberikan
obat.

41. Contoh kasus:
 Suatu obat baru yang dapat membantu masalah
gangguan tidur (soporific drug) telah ditemukan.
Untuk mengetahui efektivitas obat tersebut,
penelitian yang melibatkan 10 pasien kemudian
diadakan.
 Lamanya waktu tidur (dalam jam) pasien
sebelum dan sesudah diberikan obat disajikan
pada tabel dibawah ini:

42.  Apakah obat baru tersebut benar-benar efektif
mengatasi masalah gangguan tidur?
No. Sebelum (0) Sesudah (1)
1. 5.1 7
2. 6.2 7
3. 4.7 5.8
4. 5.7 5.8
5. 6.2 6.1
6. 4.3 8.7
7. 3.7 9.2
8. 6.5 8.1
9. 3.4 8
10. 3.8 7.2

43.  Sebelum melakukan analisis data dengan uji-t
berpasangan, terlebih dahulu kita uji apakah
kedua data menyebar normal atau tidak.
 Statistik uji yang digunakan adalah Lilliefors
(Kolmogorov-Smirnov) normality test.
 Hipotesis uji normalitas:
 H0 : Data menyebar normal
 H1 : Data tidak menyebar normal
 α = 0.05

44.  Hasil uji normalitas data adalah sebagai berikut:
 Lilliefors (Kolmogorov-Smirnov) normality test
 data: sebelum
 D = 0.1597, pvalue = 0.6658
 Lilliefors (Kolmogorov-Smirnov) normality test
 data: sesudah
 D = 0.1405, pvalue = 0.8325

45.  Oleh karena p-value uji normalitas untuk data
sebelum dan sesudah pemberian obat lebih besar
dari 0.05, maka kesimpulan statistika yang
diambil adalah TERIMA H0 , artinya dapat
dikatakan bahwa kedua data berasal dari
populasi yang menyebar normal.
 Dengan demikian, uji-t berpasangan dapat
diterapkan.
 Perlu diketahui bahwa pada kasus uji-t
berpasangan, kita tidak perlu melakukan
pengujian mengenai homogenitas ragam
(populasi) dari kedua data tersebut.

46.  Hipotesis dari kasus ini dapat dituliskan:
 H0 : μ1 − μ0 = 0
 H1 : μ1 − μ0 ≠ 0
 α = 0.05
 H1 berarti bahwa selisih sebenarnya dari kedua
rata-rata tidak sama dengan nol.

47.  Analisis data menggunakan uji-t berpasangan
(paired t-test) disajikan sebagai berikut:
 Paired t-test
 data: sesudah and sebelum
 t = 3.6799, df = 9, pvalue = 0.005076
 alternative hypothesis: true difference in means
is not equal to 0
 95 percent confidence interval:
 0.8976775 3.7623225
 sample estimates:
 mean of the differences
 2.33

48.  P-value dari uji-t berpasangan di atas adalah
0.005076, yaitu lebih kecil dari 0.05.
 Dengan demikian, kesimpulan statistika yang kita
ambil adalah TOLAK H0 . Hal ini berarti bahwa
selisih lama waktu tidur sebelum dan sesudah
diberi obat untuk setiap individu tidak sama
dengan nol.
 Dengan demikian, obat tersebut terbukti efektif
membantu gangguan tidur.
 Sedangkan lama waktu tambahan tidur apabila
seseorang mengkonsumsi obat tersebut berkisar
antara 0.897 hingga 3.76 jam dibandingkan lama
waktu tidur tanpa mengkonsumsi obat tersebut,
dengan tingkat kepercayaan sebesar 95%.

49. Terima Kasih
Copyright © 2008 Deny Kurniawan
http://ineddeni.wordpress.com