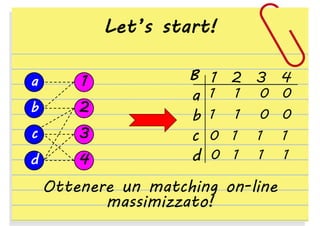
Il documento discute algoritmi per il matching in grafi bipartiti, evidenziando le differenze tra approcci on-line e off-line. Viene presentato l'algoritmo di ranking come il miglior algoritmo on-line per ottenere un matching, rispetto a metodi deterministici e randomizzati. Infine, si sollevano domande aperte riguardanti le prestazioni dell'algoritmo in varie configurazioni di grafo.

1. AN OPTIMAL ALGORITHM
FOR ON-LINE BIPARTITE
MATCHING
Dall’articolo scritto da:
Karp, Umesh e Vijay Vazirani

2. I Grafi
Un grafo è un insieme di elementi detti
nodi o vertici collegati fra loro da archi.
Più formalmente, si dice grafo una coppia
ordinata G =(V,E) di insiemi, con V insieme
dei nodi ed E insieme degli archi, tali che gli
elementi di E siano coppie di elementi di V.
b
a
d
c
e V = {a, b, c, d, e}
E = {(a,b), (a,c), (b,c),
(b,d), (d,e)}

3. Grafi Bipartiti
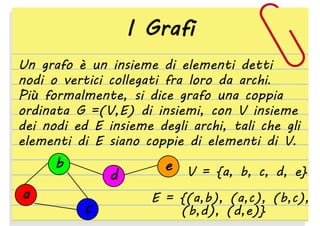
Un grafo si dice bipartito se esiste una
partizione (V1, V2) di V tale che ogni
arco [i, j] ϵ E collega un vertice i ϵ V1
ad un vertice j ϵ V2.
a
b
c
1
2
3

4. Grafi Bipartiti
Si dimostra che G è bipartito se e solo
se non contiene cicli dispari, cioè cicli
formati da un numero dispari di lati.
In generale sono grafi bipartiti:
• i grafi non orientati aciclici, quindi
anche gli alberi;
• i grafi ciclici con un numero pari di
vertici.

5. Matching in un Grafo
Bipartito
Dato un grafo bipartito con sottoinsiemi V1
e V2, si dice matching completo di V1 in V2
un insieme di archi senza estremi in comune,
aventi la caratteristica di collegare ciascun
elemento di V1 con un elemento di V2, allora
|V1|<=|V2|.
1
a
b
2
3

6. Matching in un Grafo
Bipartito
Si ha un matching perfetto, invece, nel caso
di un matching completo e |V1|=|V2|.
Si ha un matching massimale quando l’insieme
M degli archi partecipanti al matching è
massimo.
1
a
b
2
c
3

7. Algoritmi per il matching
Algoritmi
on-line
Algoritmi
off-line

8. Let’s start!
a
1
b
2
c
3
d
4
B 1 2 3 4
a
b
c
d
1
1
0 0
1
1
0 0
0 1
0 1
1
1
Ottenere un matching on-line
massimizzato!
1
1

9. Algoritmi deterministici
Un algoritmo Greedy, è quindi deterministico,
assegna sempre, se è possibile, una girl ad un
boy, scelto tra quelli idonei. Allora il
matching ottenuto sarà al minimo di n/2.
a
1
1
2
1
b 0 1
c 0 0
d 0 0
3
1
4
1
1
1
1
1
1
1
n/2
n/2
un avversario può
limitare qualsiasi
algoritmo
deterministico ad un
matching di n/2.

10. Randomized VS Adaptive
1 2 3 4
a
b
c
d
0
0
1
1
0
1
1
1
0
0
0
0
1
1
1
1
1 2 3 4
a
b
c
d
0
0
0
1
0
1
0
0
0
0
0
0
n/2 + O(logn)
1
0
0
0

11. Algoritmo Ranking
Inizializzazione: sceglie
una permutazione random
dei nodi boy e assegna ad
ognuno di essi una priorità
Matching: all’arrivo di ogni
nodo girl, esso viene
accoppiato con il boy idoneo
avente priorità più alta
(se ne esistono)

12. Algoritmo Ranking
Perché scegliere un algoritmo Ranking e non
Random?
Mentre Random ha praticamente le stesse
performance, scarse, di un algoritmo
deterministico greedy, Ranking ha prestazioni
migliori dato che contiene un meccanismo
implicito che tende a favorire quei nodi
attualmente idonei che non lo sono stati
spesso in passato.

13. Considerazioni...
Supponiamo che le colonne siano ordinate in
ordine crescente di priorità e che le righe arrivino
in ordine random e vengano accoppiate alla colonna
idonea con priorità più alta.
Allora:
•l’insieme di girls accoppiate dal Ranking è un
superset di qualsiasi altro algoritmo che prevede
il rifiuto;
•la dimensione del matching prodotto dal Ranking
è minima per alcune matrici triangolari superiori.

14. Caso Pessimo
e Performance
Dimostrando che il matching tramite
Ranking è minimo nel caso di matrici
triangolari superiori complete si dimostra
anche che esso garantisce le migliori
performance.
|M|=(n+|D|)/2
E[|M|] = n/2+1/2 E[|D|]

15. Algoritmo Early
rmance
e perfo
zzare l
li
derare
di ana
e consi
è util
o scopo
All
anking
R
Early.
oritmo
iamata
dell’alg
nte ch
a varia
una su
Tale variante rifi
uta di accoppiare
la riga
i se arriva dopo
che la colonna i
è già
stata accoppiata
.

16. Algoritmo Early
Attraverso Early è possibile trovare un
lower–bound per E[|M|] calcolando un
lower-bound per E[|D|].
wit
= Pr[W(σ,i) = t]
Pr[la riga i e la colonna i
vengono entrambe
accoppiate] = ∑t/n wit
wt = ∑ wit
i
E[|D|] = ∑t/n wt
t
La dimensione minima del matching sarà
(2-√2)n

17. Algoritmo Early
L’analisi effettuata parte dall’assunzione
pessimistica che le prime an righe ad
arrivare saranno tutte accoppiate.
Tuttavia nella realtà è improbabile che
ciò avvenga.
Eseguendo, allora, un’analisi più precisa si
ottiene tale risultato: n(1-1/e)+O(n)

18. Algoritmo Early e Ranking
Dato che l’algoritmo Early è un algoritmo
che prevede il rifiuto rispetto al Ranking,
possiamo dire che il matching prodotto
da quest’ultimo, su una matrice B nxn
per il quale il matching massimo è m<=n,
sarà al minimo pari ad m(1-1/e)+O(m)

19. Algoritmi on-line per il
matching bipartito
L’algoritmo Random ha le stesse performance
del Ranking su una matrice T triangolare
superiore completa. Tuttavia per il Ranking
operare su T costituisce il caso pessimo.

20. Algoritmi on-line per il
matching bipartito
Allora Ranking è sicuramente l’algoritmo
on-line di matching bipartito ad avere
le migliori performance.

21. Algoritmi on-line per il
matching bipartito
Inoltre, dato che gli algoritmi Greedy
hanno le stesse performance dell’algoritmo
Random, essi sono sicuramente i migliori
algoritmi deterministici di matching
bipartito on-line.

22. Open Questions
Nell’ambito di questo studi rimangono
comunque delle domande aperte a cui
dover dare ancora una risposta:
• dare in input una matrice triangolare
superiore completa è il caso peggiore
per il Ranking?
• il Ranking è un algoritmo on-line
ottimo anche per il matching in grafi
non bipartiti?